Journal of Modern Physics
Vol. 4 No. 10 (2013) , Article ID: 38873 , 8 pages DOI:10.4236/jmp.2013.410171
Discussion of Direct Numerical Simulation Method for Supercritical Carbon Dioxide Jet Flow*
1College of Petroleum Engineering, China University of Petroleum, Qingdao, China
2Institute of Mechanics, Chinese Academy Science, Beijing, China
Email: gaohui@upc.edu.cn
Copyright © 2013 Hui Gao, Guoqing Hu. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 4, 2013; revised August 6, 2013; accepted September 7, 2013
Keywords: Direct numerical simulation; supercritical carbon dioxide jet flow; nonconservative compressible Navier-Stokes equations
ABSTRACT
A kind of direct numerical simulation method suitable for supercritical carbon dioxide jet flow has been discussed in this paper. The form of dimensionless nonconservative compressible Navier-Stokes equations in a two-dimensional cartesian coordinate system is derived in detail. High accurate finite difference compact schemes based on non-uniform grid system are introduced to solve the equations. The simulation results of the three vortex pairing phenomenon of plane mixing layer and a compressible axisymmetric jet flow field show that the discussed numerical simulation method is feasible to calculate the supercritical carbon dioxide jet fluid. And it is found that the difficulties of splitting the convective terms in conservation Navier-Stokes equations, which are brought by the supercritical carbon dioxide fluid pressure state equation, can be avoided by solving the nonconservative compressible Navier-Stokes equations.
1. Introduction
Supercritical carbon dioxide fluid refers to carbon dioxide fluid at more than the critical temperature 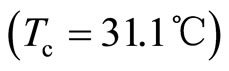 and critical pressure
and critical pressure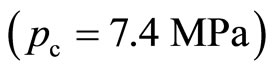 . Its density is close to liquid, its diffusivity and viscosity is close to gas, and it has strong solvency. In recent years, much attention has been paid to the application of supercritical CO2 jet fluid technology in the petroleum engineering [1]. Supercritical CO2 jet fluid is a kind of high pressure fluid jet to break rock. In the numerical simulation research for this kind of high pressure fluid jet to break rock problem [1], the jet flow field should be simulated starting from initial and boundary conditions, and the fluid forces on the surface of rock should be calculate, which is used as a part of the boundary conditions to calculate the rock mechanics. Visiblely, presenting and even predicting the detail structure form of supercritical co2 jet flow is very necessary. At present, the mechanism studies of supercritical co2 jet to break rock have been carried out by some researchers. Some questions have been met as the supercritical carbon dioxide fluid flow field is calculated using Fluent software, such as: the flow field calculation accuracy is not enough, the flow of the large scale structure are vague, and it is more difficult to capture the flow of small scale structure. It is difficult to understand structure properties of supercritical carbon dioxide fluid only relying on commercial software. Therefore, it is necessary to extract a jet flow problem closely related to fluid mechanics from supercritical co2 jet drilling in the engineering, and to do some thorough theoretical study using numerical simulation method of computational fluid dynamics.
. Its density is close to liquid, its diffusivity and viscosity is close to gas, and it has strong solvency. In recent years, much attention has been paid to the application of supercritical CO2 jet fluid technology in the petroleum engineering [1]. Supercritical CO2 jet fluid is a kind of high pressure fluid jet to break rock. In the numerical simulation research for this kind of high pressure fluid jet to break rock problem [1], the jet flow field should be simulated starting from initial and boundary conditions, and the fluid forces on the surface of rock should be calculate, which is used as a part of the boundary conditions to calculate the rock mechanics. Visiblely, presenting and even predicting the detail structure form of supercritical co2 jet flow is very necessary. At present, the mechanism studies of supercritical co2 jet to break rock have been carried out by some researchers. Some questions have been met as the supercritical carbon dioxide fluid flow field is calculated using Fluent software, such as: the flow field calculation accuracy is not enough, the flow of the large scale structure are vague, and it is more difficult to capture the flow of small scale structure. It is difficult to understand structure properties of supercritical carbon dioxide fluid only relying on commercial software. Therefore, it is necessary to extract a jet flow problem closely related to fluid mechanics from supercritical co2 jet drilling in the engineering, and to do some thorough theoretical study using numerical simulation method of computational fluid dynamics.
So far, there are two kinds of numerical simulation methods for supercritical co2 flow both at home and abroad. One is direct numerical simulation method, the other is turbulence model numerical simulation method. Direct numerical simulation is to solve directly the Navier-Stokes equations without introducing any closed models in the scales of turbulence grid size. At present, there are seldom research results on the supercritical co2 flow direct numerical simulation results, in which the representative results are as following. In 2006 Ri Shinryo et al. [2], and in 2008 Xinliang Li et al. [3], carried out direct numerical simulation of supercritical carbon dioxide channel flow on the background of water cooled reactor. In reference [3], the full compressible Navier-Stokes equations and Peng-Robison state equation were calculated numerically; according to the application background, the incoming flow temperature values were 43˚C and 41˚C, the incoming flow pressure were 8 Mpa, the Mach number was 0.2, and the calculated Reynolds number was 2800; this paper gives a detailed quantitative turbulent statistical results; this paper points out that, however, due to the Mach number is low, the strict time step restricted conditions affected the computing efficiency of direct numerical simulation. Relatively, the researchers usually study supercritical carbon dioxide fluid using turbulence model numerical simulation method. Such as in 2003 DANG C et al. [4] simulated supercritical CO2 cooling heat transfer process using several turbulence models; in 2002 S. M. Liao et al. [5] simulated laminar convective heat transfer of supercritical carbon dioxide in a small vertical tube.
Based on the above content, a kind of direct numerical simulation method suitable for supercritical carbon dioxide jet flow is discussed in this paper. Supercritical carbon dioxide jet flow belongs to compressible flow problems. Navier-Stokes equations for compressible fluid flow can be expressed into two forms: conservation and nonconservation. In the general theory of fluid mechanics, it is same in nature to use the conservation form or the nonconservation form of Navier-Stokes equations, because it can be derived from one form to another form through simple derivation. However, which form of Navier-Stokes equations would be used is very important in computational fluid mechanics [6].
The conservative compressible Naver-Stokes equations are usually used to simulate compressible flows for a perfect gas. Because experience shows that the calculated flow field is generally smooth and stable using the conservative equations. In some literatures [7,8], a class of effective numerical simulation methods are proposed for conservative compressible Navier-Stokes equations. For example, In literature [8], a finite difference discrete method is used for the conservative compressible NavierStokes equations: the convective terms are splitted firstly using Stegger-Warming method and discreted secondly using the fifth order upwind difference scheme; the viscous terms are discreted using the sixth order central difference scheme; the time terms are discreted using the third order Runge-Kutta method. The conservative compressible Naver-Stokes equations can also be used to simulate compressible flows for some real gas. For example, In literature [9], a numerical calculation method for real gas flow was given when the pressure state equation is discribed as , where p, ρ and e denote the pressure, density and internal energy, respectively. For high resolution numerical formats, characteristics of Jacobian matrix of the convection item are usually needed to be analyzed. In literature [9], the characteristics of Jacobian matrix was analyzed for the real gas with the pressure state equation as
, where p, ρ and e denote the pressure, density and internal energy, respectively. For high resolution numerical formats, characteristics of Jacobian matrix of the convection item are usually needed to be analyzed. In literature [9], the characteristics of Jacobian matrix was analyzed for the real gas with the pressure state equation as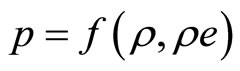 . On the basis of analyzing the characteristics of Jacobian matrix, suitable numerical scheme can be selected to solve the discreted conservative compressible Navier-Stokes equations. In these methods such as in literature [8] or [9], it is not easy for solving diagonalization characteristic value of the Jacobian matrix and diagonalizing the Jacobian matrix, because the Jacobian matrix defined in conservation variables is usually extremely complex.
. On the basis of analyzing the characteristics of Jacobian matrix, suitable numerical scheme can be selected to solve the discreted conservative compressible Navier-Stokes equations. In these methods such as in literature [8] or [9], it is not easy for solving diagonalization characteristic value of the Jacobian matrix and diagonalizing the Jacobian matrix, because the Jacobian matrix defined in conservation variables is usually extremely complex.
It is usually difficult to obtain a pressure state equation just as 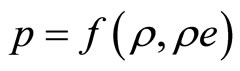 described in literature [9] for non perfect gas, especially for supercritical carbon dioxide fluid. However, the eigenvalue and the diagonalization of the jacobian matrix has an important role in numerical simulation of conservative compressible Navier-Stokes equations. A numerical simulation method using high accurate finite difference schemes for solving nonconservative compressible Navier-Stokes equations is performed in this paper, in order to avoid the difficulties of splitting the convective terms in conservation NavierStokes equations, which is brought by the supercritical carbon dioxide fluid pressure state equation.
described in literature [9] for non perfect gas, especially for supercritical carbon dioxide fluid. However, the eigenvalue and the diagonalization of the jacobian matrix has an important role in numerical simulation of conservative compressible Navier-Stokes equations. A numerical simulation method using high accurate finite difference schemes for solving nonconservative compressible Navier-Stokes equations is performed in this paper, in order to avoid the difficulties of splitting the convective terms in conservation NavierStokes equations, which is brought by the supercritical carbon dioxide fluid pressure state equation.
2. Nonconservative Form of Dimensionless Compressible Navier-Stokes Equations
For convenience, the form of dimensionless nonconservative compressible Navier-Stokes equations in a twodimensional cartesian coordinate system is only presented in this paper.
The detail derivation process of nonconservative compressible Navier - Stokes equations has been showed in literature [6]. Firstly, the dimensional nonconservative compressible Navier - Stokes equations in a two-dimensional cartesian coordinate system can be obtained as following:
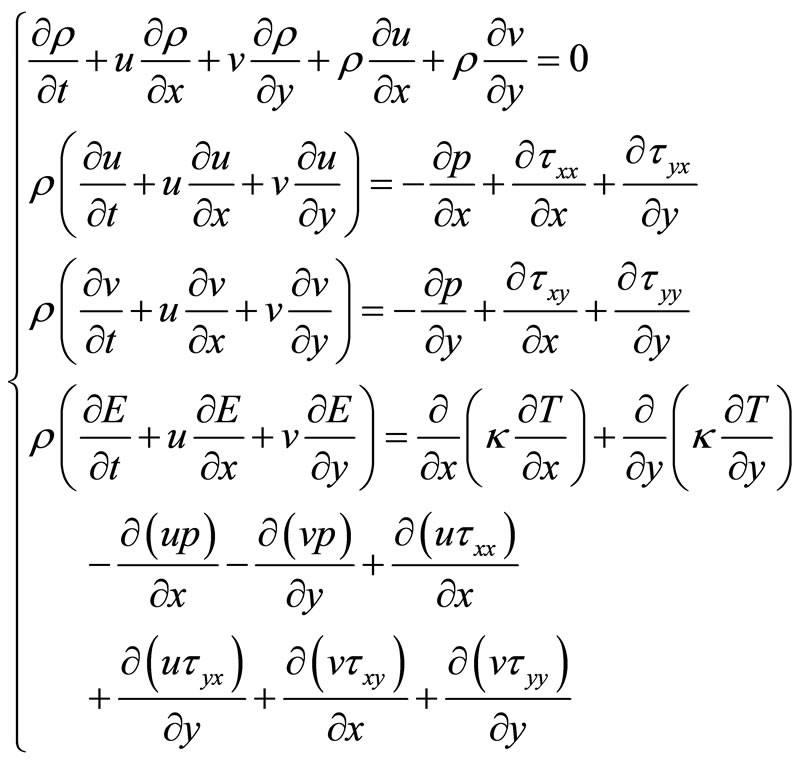 (1)
(1)
In equations (1), u and v, respectively, is corresponding to the speed in x and y directional coordinate. ρ and T, respectively, is corresponding to the density and the temperature. t is corresponding to the time. The pressure p is determined by the pressure state equation. The heat transfer coefficient 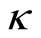 is defined as
is defined as
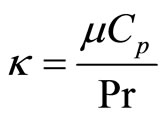 .
.
μ is viscosity, Cp is specific heat at constant pressure, Pr is a dimensionless number named as Prandtl number. In equations (1), there is
 ,
, .
.
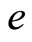 is internal energy. In equations (1),
is internal energy. In equations (1), 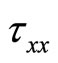 ,
, 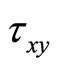 ,
, 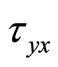 and
and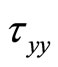 , respectively, is the weight of the viscous stress tensor, which is expressed as following:
, respectively, is the weight of the viscous stress tensor, which is expressed as following:
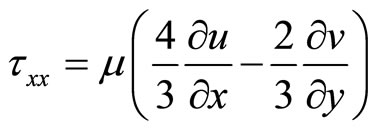 ,
,
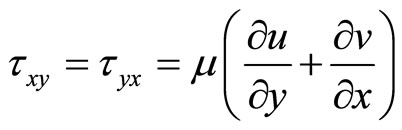
and
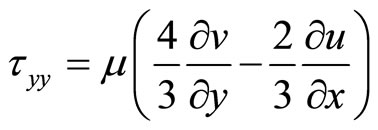 .
.
In the thermal equilibrium state system, the internal energy has the general form as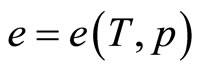 . It is known that the pharmaceutical units of Cp is
. It is known that the pharmaceutical units of Cp is
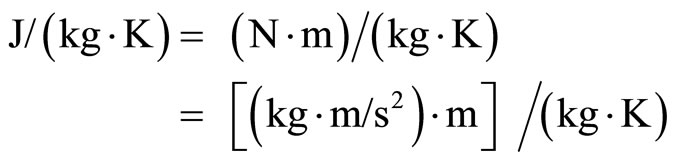 and the pharmaceutical units of T is K. So the pharmaceutical units of
and the pharmaceutical units of T is K. So the pharmaceutical units of 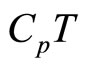 is m2/s2 just as similar as that of
is m2/s2 just as similar as that of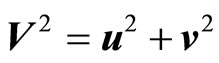 . According to the homogeneity principle of dimension, internal energy e can be defined as
. According to the homogeneity principle of dimension, internal energy e can be defined as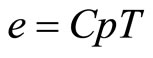 . So another form of equations (1) can be obtained as following:
. So another form of equations (1) can be obtained as following:
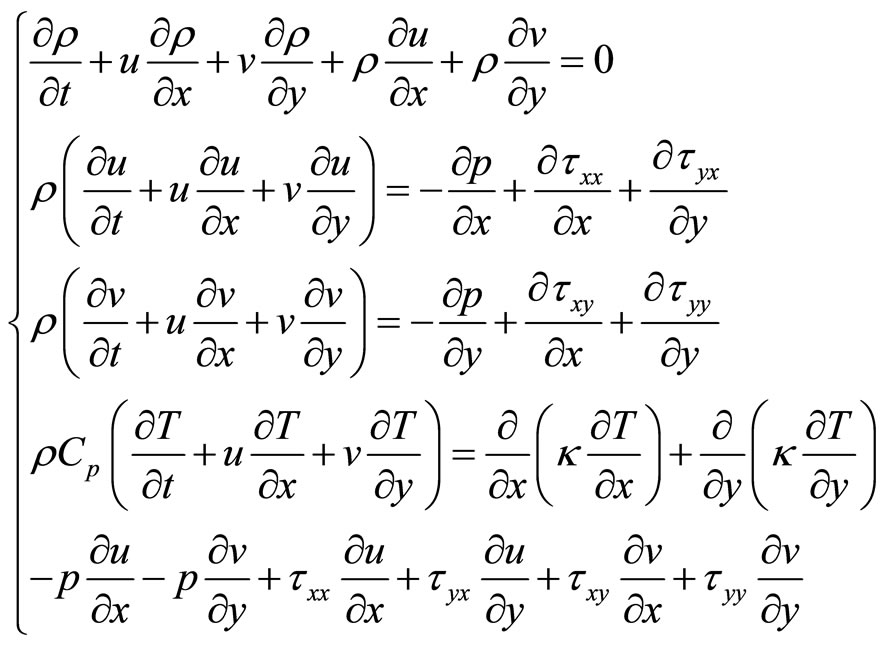 (2)
(2)
Equations (2) should be changed into dimensionless form in order to be used to simulate some flow fields. The dimensionless system is chosen here as following:
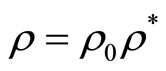 ,
, 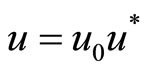 ,
,  ,
,
 ,
,  ,
, 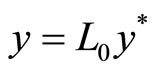 ,
,
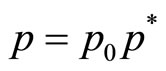 ,
,  ,
, 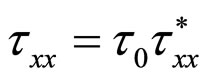 ,
,
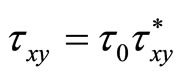 ,
, 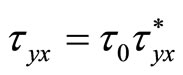 ,
,  ,
,
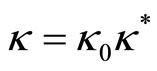 and
and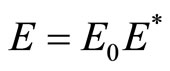 .
.
Here the physical quantities with a subscript “0” are corresponding characteristic quantities; and the physical quantities with a subscript “*” are corresponding dimensionless quantities. Thus the equations (2) can be written as following:
 (3)
(3)
In equations (3), the characteristics of time  can be instead of
can be instead of
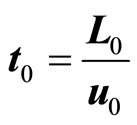 and the characteristics of viscous stress
and the characteristics of viscous stress 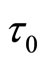 can be instead of
can be instead of
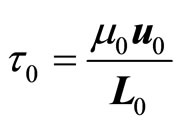 .
.
So the following equations can be obtained as following:
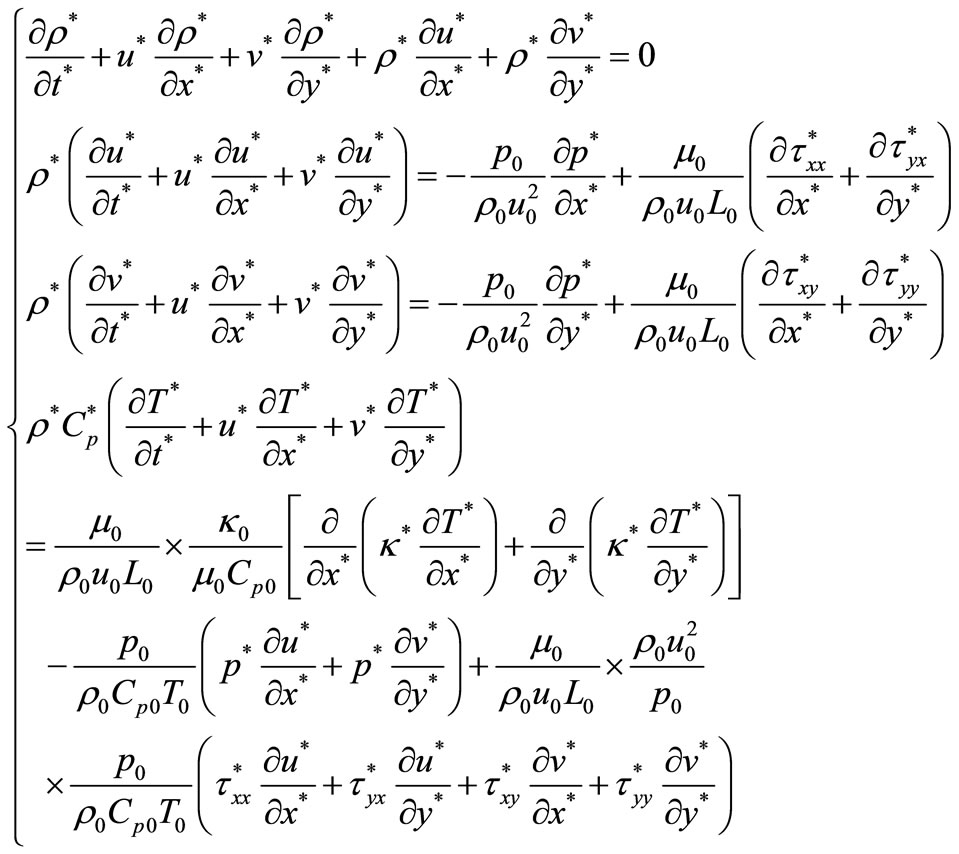 (4)
(4)
In equations (4), the Reynolds number is defined as
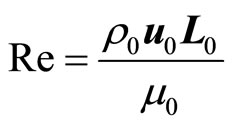 .
.
According to the definitions of Mach number as
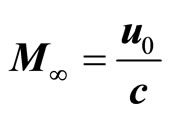
and speed of sound as
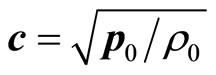 the definition of the pressure characteristics can obtained as
the definition of the pressure characteristics can obtained as
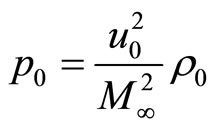 .
.
So there are
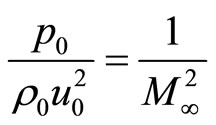 and
and 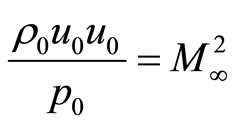
in equations (4). According to the expression of
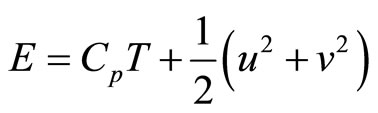 and
and 
in equations (1), the expression of
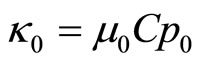 and
and 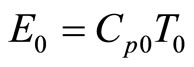
can be obtained. So there is
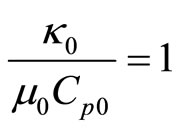
in equations (4).
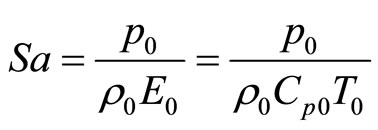
can be defined in equations (4). It is known that the pharmaceutical units of pressure 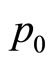 is
is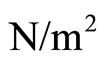 , the pharmaceutical units of density
, the pharmaceutical units of density 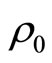 is
is , the pharmaceutical units of specific heat at constant pressure
, the pharmaceutical units of specific heat at constant pressure 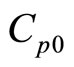 is
is
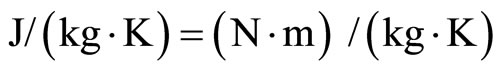 and the pharmaceutical units of temperature
and the pharmaceutical units of temperature  is K, so it can be found that Sa is also a dimensionless number.
is K, so it can be found that Sa is also a dimensionless number.
Based on the above analysis, the form of dimensionless nonconservative compressible Navier-Stokes equations in a two-dimensional cartesian coordinate system can be presented as following:
 (5)
(5)
In equations (5), there are some expressions as following:
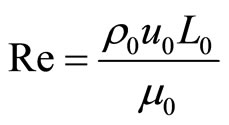 ;
;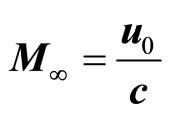 ;
;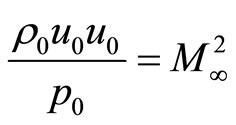 ;
;
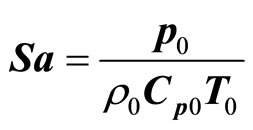 ;
;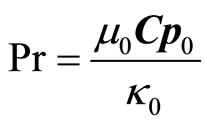 ;
; ;
;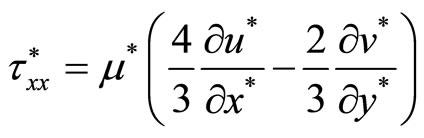 ;
;
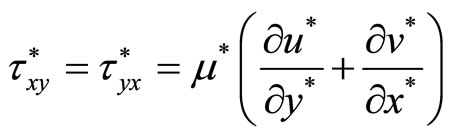 ;
;
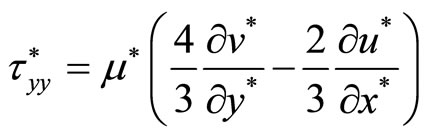 .
.
3. Finite Difference Discrete Method of Nonconservative Compressible Navier-Stokes Equations
In order to obtain better numerical simulation results, high accurate compact finite difference schemes can be used to discrete equations (5). Because non-uniform grids ussually need to be used for numerical simulation of complex flow field, a kind of high accuracy difference scheme based on non-uniform grid system can be used [8]. If the discrete grid points in x direction are noted by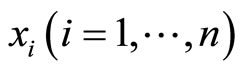 , the definition of
, the definition of  and
and  can be obtained.
can be obtained.
3.1. The 5th Order Upwind Compact Difference Scheme Based on Non-Uniform Grid System
The one order spatial derivatives on the left of equations (5), such as
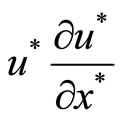 have the nature of the hyperbolic equation. So the basic characteristics of the disturbance wave propagation should be considered to using the upwind difference scheme to discrete the one order spatial derivatives on the left of equations (5). For example, the frozen coefficient method can be used to deal with the term of
have the nature of the hyperbolic equation. So the basic characteristics of the disturbance wave propagation should be considered to using the upwind difference scheme to discrete the one order spatial derivatives on the left of equations (5). For example, the frozen coefficient method can be used to deal with the term of
 , i.e.
, i.e.
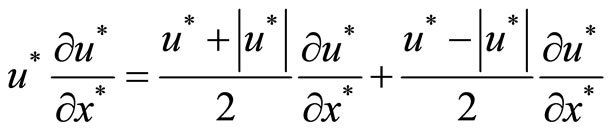 .
.
Because the coefficient
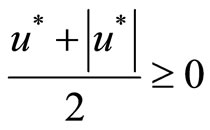 the 5th order upwind compact backward difference scheme based on non-uniform grid system can be used to discrete the term
the 5th order upwind compact backward difference scheme based on non-uniform grid system can be used to discrete the term
 , i.e.
, i.e.
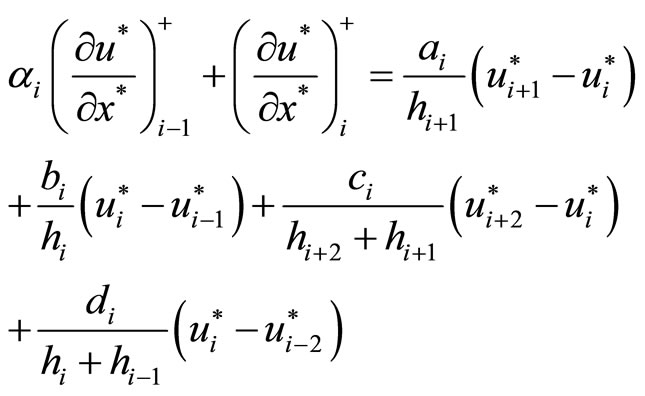 (6)
(6)
Using Taylor series expansion, the coefficients as ,
, 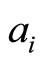 ,
,  ,
, 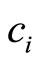 and
and 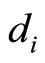 in equation (6) can be solved through the algebraic equations, i.e.
in equation (6) can be solved through the algebraic equations, i.e.
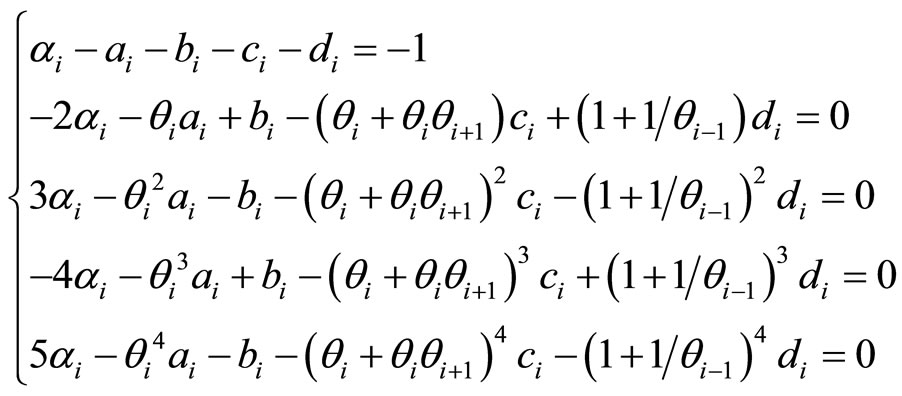 (7)
(7)
Because the coefficient
 the 5th order upwind compact forward difference scheme based on non-uniform grid system can be used to discrete the term
the 5th order upwind compact forward difference scheme based on non-uniform grid system can be used to discrete the term
 , i.e.
, i.e.
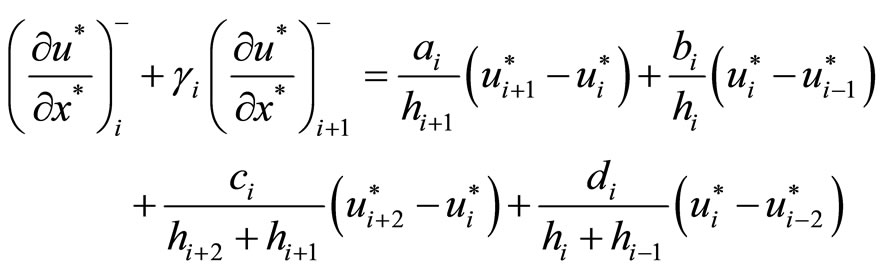 (8)
(8)
Using Taylor series expansion, the coefficients as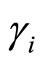 ,
, 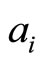 ,
, 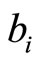 ,
, 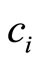 and
and 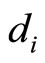 in equation (8) can be solved through the algebraic equations, i.e.
in equation (8) can be solved through the algebraic equations, i.e.
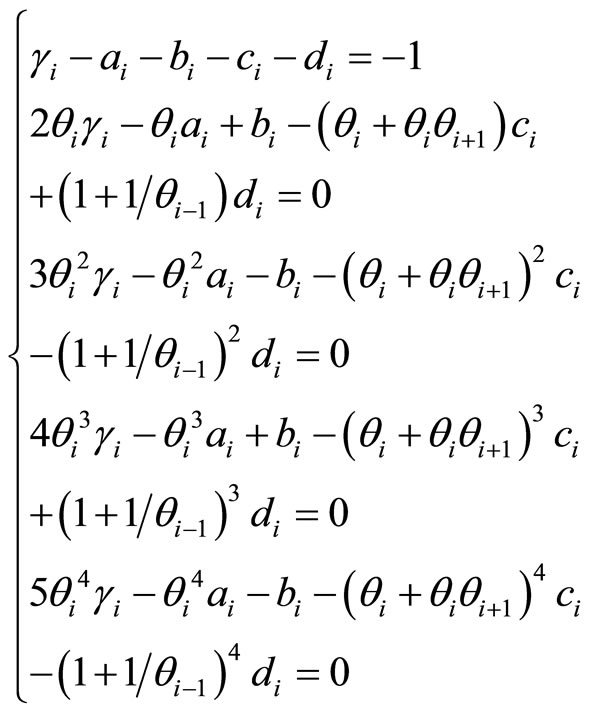 (9)
(9)
3.2. The 6th Order Symmetric Compact Difference Scheme Based on Non-Uniform Grid System
The 6th order symmetric compact difference scheme based on non-uniform grid system can be used to discrete the spatial derivative terms on the right in the equations (5). For example, the term of
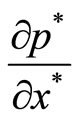
can be dealed with as following:
 (10)
(10)
Using Taylor series expansion, the coefficients as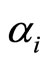 ,
, 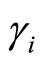 ,
,  ,
,  ,
, 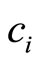 and
and 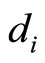 in equation (10) can be solved through the algebraic equations, i.e.
in equation (10) can be solved through the algebraic equations, i.e.
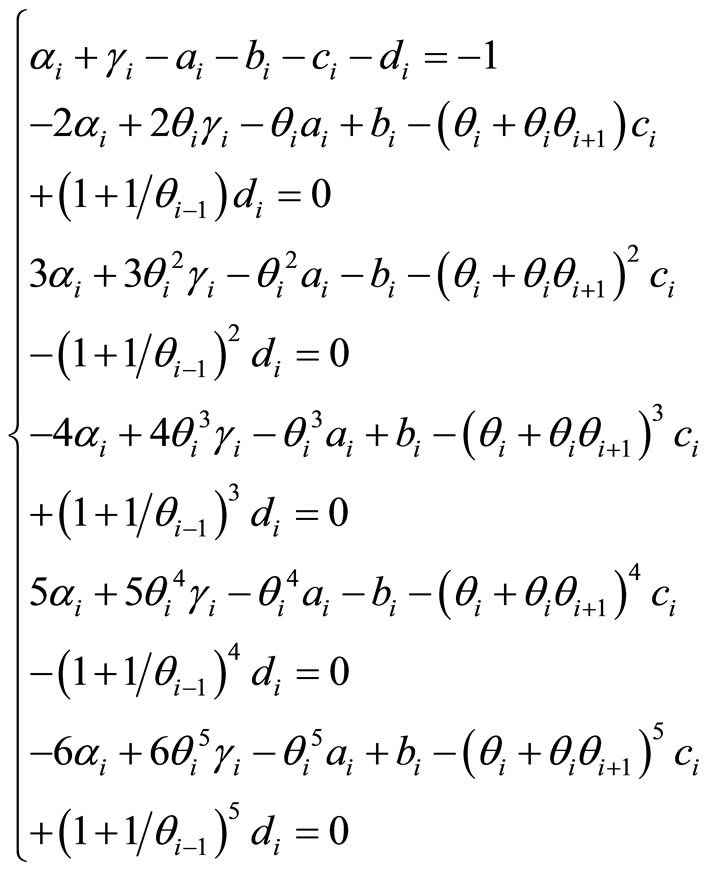 (11)
(11)
3.3. The 3th Order Accurate Rungge-Kutta Method
The 3th order accurate Rungge-Kutta method can be used to discrete the time terms on the left in the equations (5) [8].
4. The Numerical Simulation Experiments
In order to verify the above numerical simulation method for the non conservative compressible Navier-Stokes equations, two numerical simulation experiments are analyzed in this paper.
4.1 Numerical Simulation of Plane Mixing Layer
The three vortex pairing phenomenon of plane mixing layer under the condition of flow Maher number  and Reynolds number
and Reynolds number 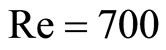 was simulated numerically using the above method.
was simulated numerically using the above method.
The initial flow field is the mean flow field adding the turbulence flow field as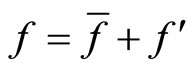 , here
, here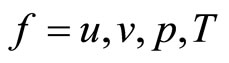 . The mean flow field is give as:
. The mean flow field is give as: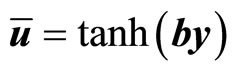 ,
, 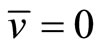 ,
,
 ,
, .
.
The turbulence flow field is given as [10]:
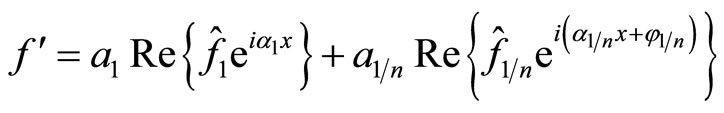 (12)
(12)
Here, 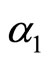 means the most unstable wave number which is obtained from the linear theory;
means the most unstable wave number which is obtained from the linear theory;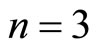 ; the characteristic functions as
; the characteristic functions as 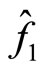 and
and  are obtained from numerical linear stability analysis; the turbulence amplitude is given as
are obtained from numerical linear stability analysis; the turbulence amplitude is given as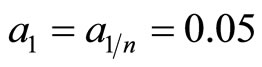 ;
;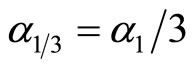 ; the phase difference
; the phase difference .
.
The periodic boundary is used in the x direction, and the no reflection boundary is used in the y direction. The computational domain is given as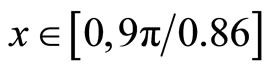 and
and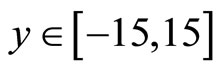 . The uniform grid is used in the x direction. The nonuniform grid is used in the y direction, and the grid is densed near
. The uniform grid is used in the x direction. The nonuniform grid is used in the y direction, and the grid is densed near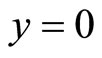 . The grid numbers are
. The grid numbers are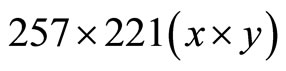 .
.
Figure 1 shows the evolutionary process for three vortex pairing of plane mixing layer, which is from flow stability to vortex formation, until to three vortex pairing.
4.2. Numerical Simulation of Plane Jet Flow
A compressible axisymmetric jet flow field was simulated numerically using the above method to slove the compressible nonconservative two-dimensional Navier - Stokes equations in the column coordinates, as the incoming flow Mach number is 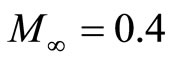 and the Reynolds number is
and the Reynolds number is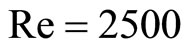 . The initial conditions are given as:
. The initial conditions are given as:
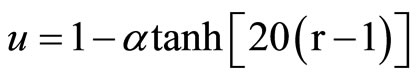 ,
, 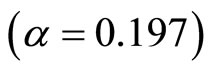 ,
,
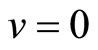 ,
, 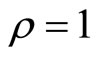 ,
,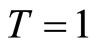 .
.
The no reflection boundary condition is used on the upper and export boundary of the flow field. According to physical characteristics of the flow, symmetrical condition is adopted for u, ρ and T, and the antisymmetric condition is adopted for v on the jet symmetric axis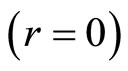 . The computational domain is given as
. The computational domain is given as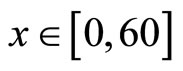 ,
, . Uniform grids are adopted in the x direction, and non-uniform grid is adopted in the r direction with local mesh encryption near the axis of symmetry. The grid number is
. Uniform grids are adopted in the x direction, and non-uniform grid is adopted in the r direction with local mesh encryption near the axis of symmetry. The grid number is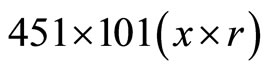 .
.
Figure 2 shows the vorticity sequence diagrams of jet near field region. It can be seen that vortex pair appears, and later, the distance between two adjacent vortex increase. That is similar to the results in the literature [11].
5. Conclusions
A kind of direct numerical simulation method suitable for supercritical carbon dioxide jet flow has been discussed in this paper. Firstly, the form of dimensionless nonconservative compressible Navier-Stokes equations in a two-dimensional cartesian coordinate system is de-
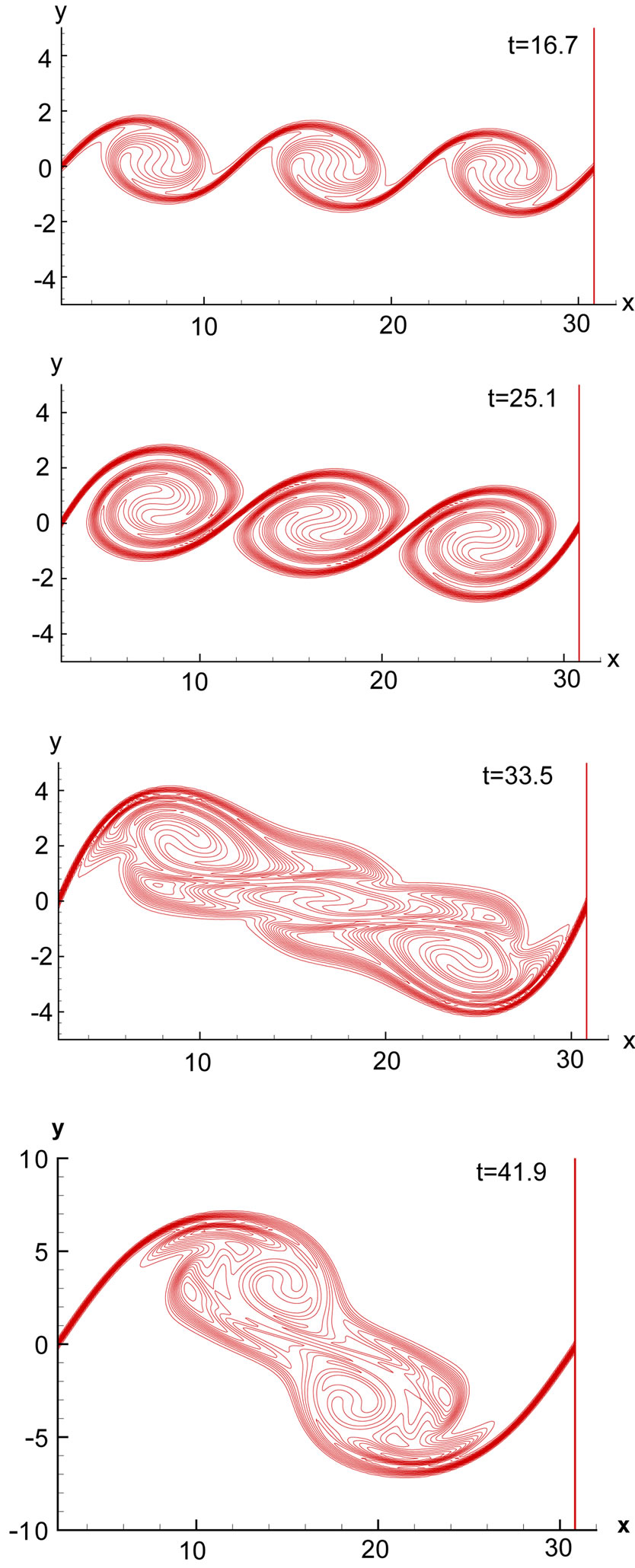
Figure 1. The three vortex pairing phenomenon of plane mixing layer.
rived in detail. High accurate finite difference compact schemes based on non-uniform grid system are introduced to solve the equations. Then, three vortex pairing phenomenon of plane mixing layer and a compressible axisymmetric jet flow field are simulated using the numerical method proposed in this paper. The relevant results show that the above numerical simulation method of solving dimensionless nonconservative compressible Navier-Stokes equations is feasible to calculate the supercritical carbon dioxide jet flow. And it is found that
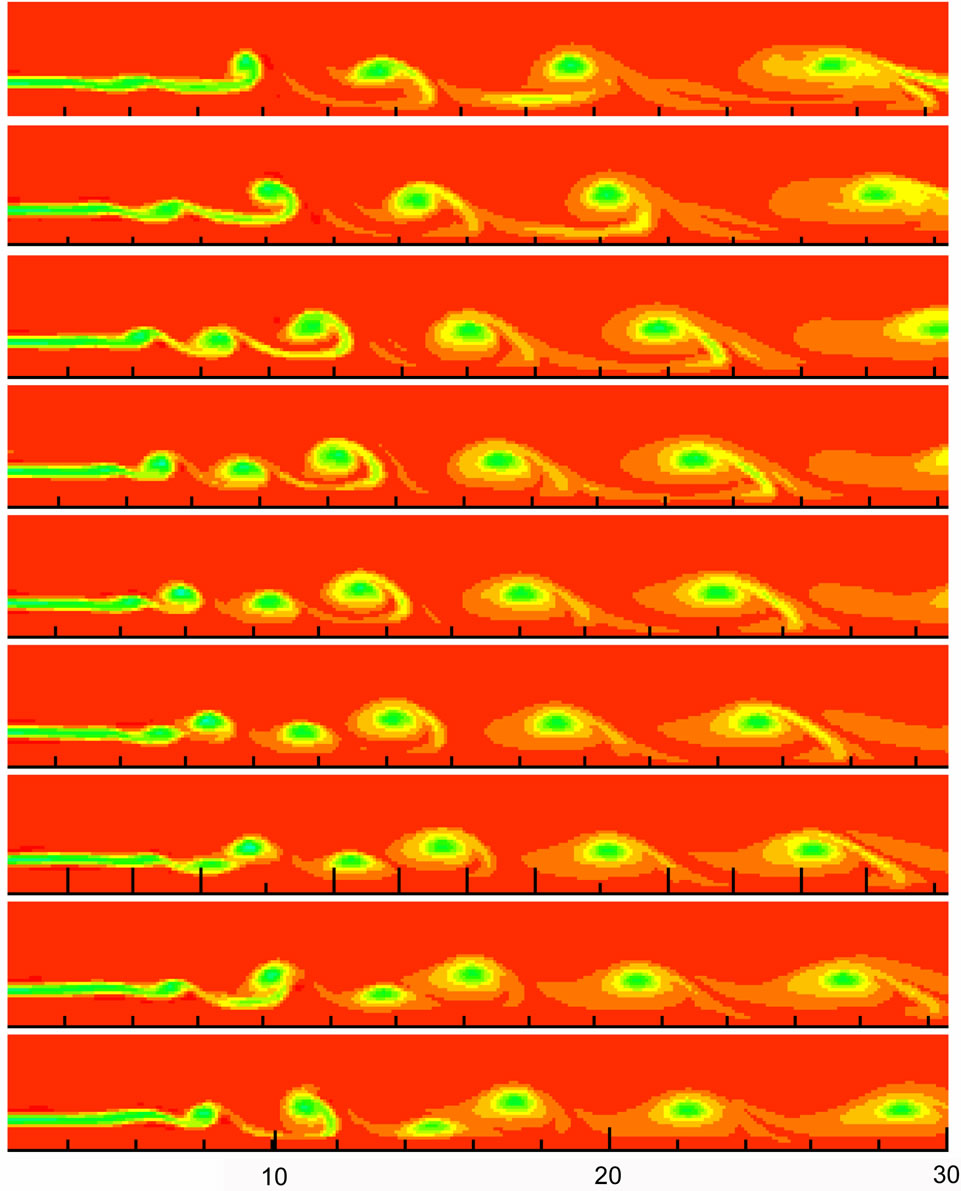
Figure 2. Vorticity evolution process of axisymmetric jet flow.
the difficulties of splitting the convective terms in conservation Navier-Stokes equations, which is brought by the supercritical carbon dioxide fluid pressure state equation, can be avoided by solving the nonconservative compressible Navier-Stokes equations.
The preliminary discussion about a direct numerical simulation method for supercritical carbon dioxide jet flow only has been performed in this paper. In the later research, the supercritical CO2 jet flow structure would be presented in detail.
REFERENCES
- H. J. Ni, R. H. Wang and Y. Q. Zhang, Applied Mathematics and Mechanics (in China), Vol. 26, 2005, pp. 1445-1452.
- R. Shinryo, H. Katsumi, T. Mamoru and M. Toshio, Proceedings of Thermal Engineering Conference, 2006, pp. 217-218.
- X. L. Li, K. Hashimoto, Y. Tominaga, M. Tanahashi and T. Miyauchi, Journal of Thermal Science and Technology, Vol. 3, 2008, pp. 112-123. http://dx.doi.org/10.1299/jtst.3.112
- C. Dang, J. F. Wang and E. Hihara, Nippon Dennetsu Shinpojiumu Koen Ronbunshu, Vol. 40, 2003, pp. 391- 392.
- S. M. Liao and T. S. Zhao, Progress in Computational Fluid Dynamics, Vol. 2, 2002, pp. 144-152. http://dx.doi.org/10.1504/PCFD.2002.003221
- J. D. Anderson, “Computational Fluid Dynamics,” Mechanical Industry Press, Beijing, 2007.
- G. Q. Hu, M. Y. Liu, D. X. Fu and Y. W. Ma, Chinese Journal of Computational Physics, Vol. 18, 2001, pp. 193-198.
- D. X. Fu and Y. W. Ma, “Computational Fluid Dynamics,” Higher Education Press, Beijing, 2002.
- Z. H. Wu, G. Guo, L. Li and Z. P. Feng, Journal of Xi An Jiaotong University (in China), Vol. 40, 2006, pp. 510- 513.
- Q. Wang, D. X. Fu and Y. W. Ma, Chinese Journal of Theoretical and Applied Mechanics, Vol. 33, 2001, pp. 1- 10.
- M y. Liu, Y. W. Ma and D. X. Fu, Chinese Journal of Computational Physics, Vol. 17, 2000, pp. 341-346.
NOTES
*Supported by National Natural Science Foundation of China (No. 11102238) and Shandong Province Natural Science Foundation of China (No. ZR2011EL035).

