ABSTRACT

In the equation U = I – A for the Mott energy, the electron-hole interaction of the successor state is missing. Adding the attractive term, the energy for disproportionation (Hubbard U), may adopt any sign. The missing term is related to the Born effect, the Madelung correction and the Lattice Enthalpy.

1. Introduction

According to Mott, “Hubbard U” is the energy for moving one electron from one site to the next. This is also referred to as the energy of “charge disproportionation”. If the system is already disproportionated, U < 0. U ≈ 0 is necessary to achieve a super-conducting state. Furthermore the well-known chemical fact that some valence states appear to be “missing” in the periodic table, for example Tl(II), Pb(III), Au(II), can be explained by U < 0.

The story of BaBiO₃ is instructive [1,2]. The BiO bond-lengths are alternating between 2.12 Å and 2.25 Å, values which are known from Bi(V) and Bi(III) compounds. Clearly Bi(IV) has undergone disproportionation:

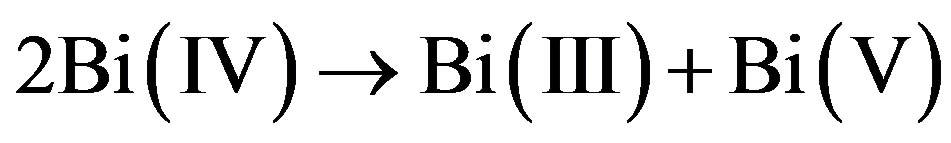(1)

Dopings that tend to equalize the bond lengths (BaBi_1–xPb_xO₃ or K_xBa_1–xBiO₃) lead to superconductivity at a quite high T_c. Pure BaBiO₃ is not superconducting, but a stable compound with two different oxidation states for bismuth, Bi(III) and Bi(V). Bi(IV) is a skipped valence state, though it is important for superconductivity.

In the “Mott insulators” CuO and NiO, on the other hand, there is no bond alternancy. Excitation over Hubbard U makes one electron jump from one metal atom to the next to form Cu(III) and Cu(I),

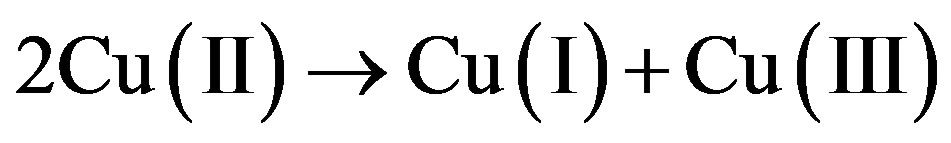(2)

Reaction (2) is endergonic, so Hubbard U is positive. There is considerable disagreement in the literature on the actual value of U and even on whether this value is uniquely defined [3,4]. About 2 eV is necessary to achieve a leap of one electron to the next site, and this makes the system photoconducting. The spectroscopic U = U_spect is about 2 eV [3]. If this is true the adiabatic U, U_ad, is very slightly above 0. U_ad is obtained at the free energy difference at equilibrium CuO distances for (CuII/CuII) and (CuI/CuIII). Structural relaxation in different oxidation states is a hallmark for the Marcus electron transfer model [5] which may be applied also to calculate Hubbard U [6].

Neither the spin coupled ground state in CuO, or for that matter in cuprates with only Cu(II) metal sites, nor the charge disproportionated state in BaBiO₃ is conducting. Superconductivity appears in doped cuprates below a rather high T_c, and it is commonly accepted that the reason is that U_ad = 0.

2. Correlation

The phrase “driving the system into a Mott insulating state” means apparently any change that makes the system insulating. The correlated state is insulating while the excited state is a metal. The conducting state is a oneelectron metallic state, where the independent-electron Bloch model (Hartree-Fock or DFT) works well. The ground state on the other hand is “driven” to an insulating local state by correlation. This popular correlation energy definition considers the uncorrelated state to be an itinerant, excited state, while the ground state is local. In other words the correlation energy would be between two different states. In the case of NiO the two states are evidenced by an insulator to metal transition at a quite high temperature, and in the cuprates by photo-induced conductivity [3].

The canonical definition of “correlation energy” is due to Löwdin [7]. In his definition correlation energy (E_corr) cannot be measured, but refers to a deficiency of the oneelectron approximation (Hartree-Fock or DFT) for a single electronic state:

(3)

E_corr > 0 since E_Hartree-Fock is obtained from the variation principle. Thus it is an upper bound to the true (nonrelativistic) solution of the Schrödinger equation E_exact.

For example the energy of the hydrogen atom is -0.5 H (-13.6 eV). The energy of the hydrogen negative ion (H^-) is -0.48 H if the HF approximation is used, while the exact value is -0.52 H. The correlation energy is thus 0.04 H (1 eV). Electron correlation makes it possible for the electrons to avoid each other, for example by being at different sides of the nucleus. E_corr refers to the ground state of H^-.

In Mott’s interpretation of Hubbard U, the focus is on the atomic integral:

(4)

This is an approximation to I - A (ionization energy minus electron affinity) and the energy for removing an electron from one site and putting it on another. For example in NiO the energy difference between the spincoupled ground state and the excited state of type Ni³⁺/Ni⁺ is equal to Hubbard U with U > 0. In BaBiO₃, on the other hand, the disproportionated state is the ground state, so U is negative. The problem is that the integral in Equation (4) cannot be negative!

There is a great current interest in calculating Hubbard U from first principles to possibly find out how U can become negative in spite of the fact that U defined in Equation (4) is very positive (≈20 eV). Looking in a table of atomic electron affinities and ionization energies we find that (the experimental) I - A is positive for all elements of the periodic table. Pairing of electrons in superconductivity would be prohibited, if Hubbard U cannot be brought to zero. Correlation is responsible according to many publications. Here we will find another explanation.

Hubbard-U and correlation energy are physically unrelated. Therefore it appears as strange that U can be overshadowed by correlation energy. The next problem is how a very negative U, that obviously exists in some compounds, can also be cancelled by correlation energy.

3. The Missing Attractive Term

Cooper originally suggested that electron-phonon interactions can solve the problem of electron repulsion in an electron pair, but he was only partly right [8]. After the discovery of “high-temperature superconductivity” (1987) [9] in systems with a very small isotope shift and whose “parent state” is localized, one realized that there must be additional contributions. P. W. Anderson already in 1975 proposed structural changes as a source of negative U [10], but did not investigate the problem further. In fact the physics behind this particular Anderson model (structural relaxation) was already known at this time as the Marcus model for electron transfer [5]. Even earlier, in papers by Landau [11] and Pekar [12], the structural modification when an electron is received or ejected, was already well understood. Their theory developed into the Holstein model (1961) [13], where the problem is treated as a one-electron problem, using the effective mass of the electron to take care of structural dependencies. The structural contribution is thus well understood, but in much current theoretical work, the structural effects are still left out. If this is done, it is impossible distinguish U_ad and U_spectr.

From 1960 we see a clear separation of theoretical approaches by physicists and chemists. Physicists prefer to express themselves in terms one-electron models (bands and conducting orbitals), while theoretical chemists prefer the Marcus model, where total (free) energies are involved and the calculations nowadays include also many-electron terms. In the CASSCF-model [14] employed in Reference [6], the latter model is used to calculate total energy surfaces according to the Born-Oppenheimer approximation.

A large part of the compensation for U > 0 is due to the Born effect, which reduces U by polarization by the medium [15]. Klimkāns and the present author carried out a calculation using the well correlated CASSCF method on a cluster with four copper ions with all their oxygen ligands included [6]. We found U_ad ≈ 0 by identifying the charge separated state in the ground state calculation. All numbers were thus obtained in a single calculation.

Calculation of ionization energy (I) and electron affinity (A) separately, and afterwards putting U = I - A, tends to give much too large numbers for U, particularly if an atomic approximation is used. The problem with positive U thus has a simple explanation. The attraction between the hole and the electron in the successor state is left out if I and A are calculated separately and U defined as I - A. The experimental U also must include the negative term from electron-hole attraction.

Analysis of the results is rather difficult. However, the CASSCF results (including correlation) suggest clearly that the most important missing term is due to the attractive electron-hole interaction after one electron has been transferred to the neighbouring copper ions. This is consistent with the dependence on the Born approximation [15] or the concentration dependence in the Madelung correction, as described by Hase and Yanagisawa [16].

We may compare to rock-salt (NaCl). At a large distance between the atoms the sodium and chlorine atoms are neutral in the total ground state. The ionization energy for Na is I = 5.14 eV while the electron affinity of Cl is only A = 3.62 eV. Therefore the neutral atomic state (Na + Cl) is stable by 1.52 eV, compared to the ionic state (Na⁺ + Cl^-). The attractive Coulomb interaction between the ions in the ionic state is distance dependent contrary to I and A. At the small distance relevant to rock-salt, the ionic state is the ground state, of course. With only one atom of each kind we obtain at the distance R between the atoms the attraction energy:

(5)

C and R are here expressed in atomic units, H for C and B for R. 1 H = 27.21 eV and 1 B = 0.52 Å. The charges are 1 and -1 in atomic units and 4pe₀ = 1. C = -5.11 eV at the interatomic distance in NaCl. The ionic form is lower by I - A + C = -3.59 eV.

We conclude that the correct definition for U is:

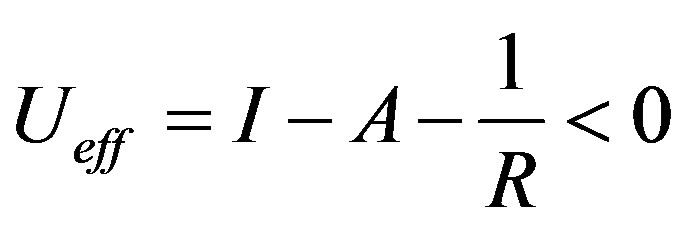(6)

The best approximation and understanding is probably obtained in the Born-Haber cycle [17], where the lattice enthalpy is calculated from available experimental data. The lattice enthalpy corresponds to the attractive term in Equation (5), and in the cases with alkali and halogen, the lattice enthalpy has a large negative value, often cancelling I - A.

The attraction in the final state is important in other physical problems as well, for example for the appearance of static electricity.

4. Applications

The recipe for getting U = 0 and superconductivity is thus simple. Raise the concentration of those atoms which are responsible for superconductivity. Then the attractive term is increased and starts to cancel U = I – A. For example in boron-doped diamond the boron impurities are responsible for the superconductivity. Ekimov found superconductivity for concentrations of about 1% [18]. Effective Hubbard U, U_eff, start to decrease for increasing concentrations from just below to above 1% [19-22].

Also thallium doped Pb_1–xTl_xS can be understood in this way [4]. When the concentration of the thallium dopant increases above 0.3% the system is superconducting. TlS is not superconducting, and this may depend on U being too negative, due to an insulating charge separated state consisting of Tl(I) and Tl(III) sites. The important condition for superconductivity is that U » 0. If U is very negative or U is very positive, the behaviour is insulating at T = 0. Disproportionated TlS or TlSe are insulators at T = 0.

Also the cuprates, where superconductivity appears after 5% oxidative doping, can be understood by the fact that U is depending on the doping level [3,23]. The charged states are lowered in energy by the doping until they are on level with the spin coupled ground state. In this case there are accurate experimental data which show how Hubbard U decreases and becomes a pseudogap, which finally merges with the superconducting gap [3].

In the case of the superconducting alkali fullerenes, A₃C₆₀, there is no dopant [24]. There is a lower charged state where disproportionation has resulted in and. Increasing the size of the alkali ion favours the spin coupled state, bringing it to interaction with the spin coupled state. Larger alkali ions A in A₃C₆₀ have a higher T_c, however, with the exception of Cs₃C₆₀. The reason is simple: the charge separated state is no longer the ground state. High pressure leads to a lower lattice constants and a larger attractive term, however, bringing the charged state to just below the spin-coupled state. The highest T_c for fullerides is then obtained.

Finally we may go back to doped BaBiO₃. In this case Hubbard U is clearly negative in the undoped case, since mixed valency exists. The charged state and the spincoupled state cannot interact sufficiently. When dopants are added to replace Bi in BaBi_1-xPb_xO₃ or barium in K_xBa_1–xBiO₃, the bond lengths are equalized and the charged state disfavoured, making the two states interact.

REFERENCES