Journal of Modern Physics
Vol.4 No.6(2013), Article ID:32975,4 pages DOI:10.4236/jmp.2013.46103
Dark Energy from Kaluza-Klein Spacetime and Noether’s Theorem via Lagrangian Multiplier Method
Department of Physics, Faculty of Science, University of Alexandria, Alexandria, Egypt
Email: Chaossf@aol.com
Copyright © 2013 Mohamed S. El Naschie. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 2, 2013; revised May 5, 2013; accepted June 3, 2013
Keywords: Dark Energy of the Schrödinger Wave; Quantum Measurement and the Missing Energy of the Cosmos; Revising Einstein’s Relativity; Kaluza-Klein Dark Energy; Lagrangian Multiplier as Dark Energy; Noether’s Theorem and Dark Energy
ABSTRACT
The supposedly missing dark energy of the cosmos is found quantitatively in a direct analysis without involving ordinary energy. The analysis relies on five dimensional Kaluza-Klein spacetime and a Lagrangian constrained by an auxiliary condition. Employing the Lagrangian multiplier method, it is found that this multiplier is equal to the dark energy of the cosmos and is given by 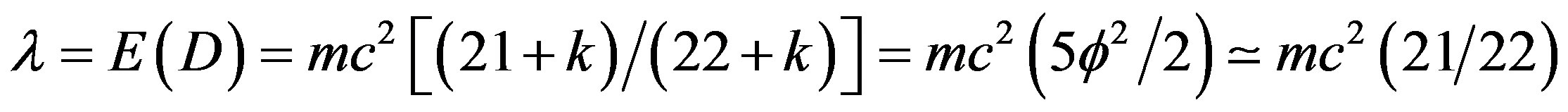 where E is energy, m is mass, c is the speed of light,
where E is energy, m is mass, c is the speed of light, 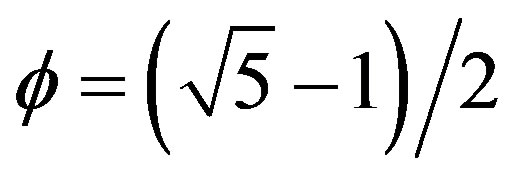 and
and 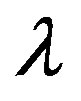 is the Lagrangian multiplier. The result is in full agreement with cosmic measurements which were awarded the 2011 Nobel Prize in Physics as well as with the interpretation that dark energy is the energy of the quantum wave while ordinary energy is the energy of the quantum particle. Consequently dark energy could not be found directly using our current measurement methods because measurement leads to wave collapse leaving only the quantum particle and its ordinary energy intact.
is the Lagrangian multiplier. The result is in full agreement with cosmic measurements which were awarded the 2011 Nobel Prize in Physics as well as with the interpretation that dark energy is the energy of the quantum wave while ordinary energy is the energy of the quantum particle. Consequently dark energy could not be found directly using our current measurement methods because measurement leads to wave collapse leaving only the quantum particle and its ordinary energy intact.
1. Introduction
The present work proposes a resolution for the missing dark energy of the cosmos [1-3], which according to the latest highly sophisticated cosmic measurements and analyses, constitutes one of, if not the most important problems facing not only cosmology but also theoretical physics at large [1-13].
There are in the meantime very strong founded feelings that the discrepancy between theory and measurement is due to the pressing need for a theory of quantum relativity [14] or if you want quantum gravity [13-19] which takes into consideration not only relativistic effect but also quantum mechanical non-locality [20] and quantum entanglement [21-25]. More general the discrepancy may be a blessing in disguise motivating and amply justifying a reappraisal of not only relativity [7-9] but also quantum mechanical foundational problems and in particular the deep meaning of the concept and reality of energy within the framework of the wave-particle duality [5,8,9] leading to dark energy-ordinary energy complementarity [15-30].
There are several strategies and corresponding theories and methods to tackle the problems of computing the density of the dark energy of the cosmos [1-12,31,32]. Roughly speaking, these could be divided globally into two categories. Either one attempts to calculate the ordinary energy and then subtract it from the total theoretical value given by Einstein’s theory [1-12] or one could try to determine the dark energy density directly without determining the corresponding magnitude of ordinary energy first. At the end the final result must of course remain the same [32].
In earlier work [9,16,31] it was established that ordinary energy density is given by 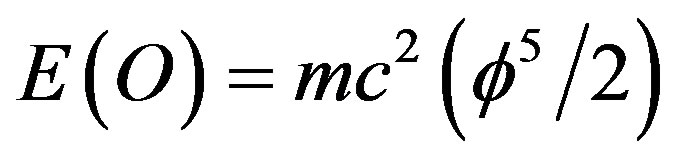 where
where 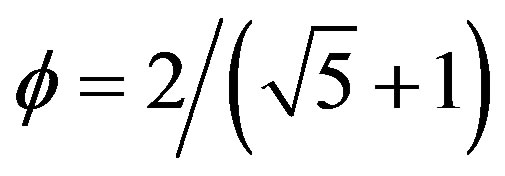 which is approximately equal to
which is approximately equal to 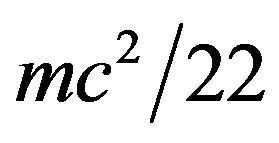 in excellent agreement with measurements [1-4]. Consequently dark energy must be given by
in excellent agreement with measurements [1-4]. Consequently dark energy must be given by
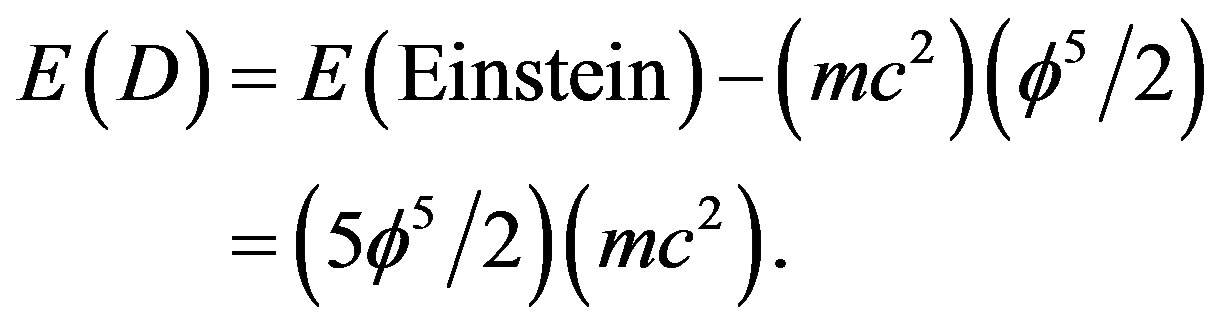 (1)
(1)
where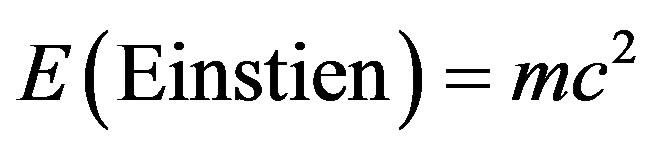 . This is approximately equal to [32].
. This is approximately equal to [32].
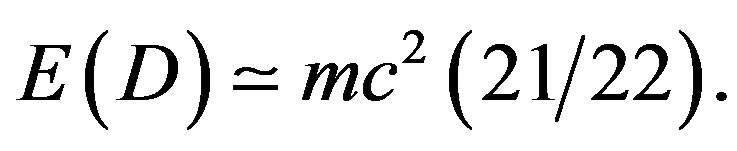 (2)
(2)
In the present work we proceed directly to calculating E(D) from first principles without any reference to ordinary energy:
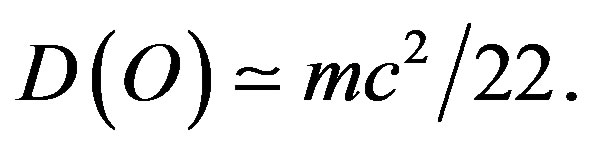
We mention in anticipation of the following sections that our main tools which we use to achieve our goal will be a combination of Noether’s theorem [5], the symmetry groups of the standard model [5] and a simple Lagrangian (£) endowed with a multiplier 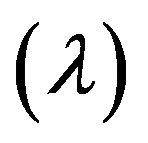 to account for certain auxiliary conditions (G) connected to symmetry and dimensions constraining the variation of the Lagrangian [9,33]. In anticipation of the main conclusion of the present work we stress that our failure to measure the dark energy is unambiguously linked to the act of measurement itself which leads to the collapse of the quantum wave which is the reason for the existence of dark energy and we are left with the ordinary energy of the quantum particle only i.e. the measured 4.5 percent of the total energy of the cosmos [1-4,16,32].
to account for certain auxiliary conditions (G) connected to symmetry and dimensions constraining the variation of the Lagrangian [9,33]. In anticipation of the main conclusion of the present work we stress that our failure to measure the dark energy is unambiguously linked to the act of measurement itself which leads to the collapse of the quantum wave which is the reason for the existence of dark energy and we are left with the ordinary energy of the quantum particle only i.e. the measured 4.5 percent of the total energy of the cosmos [1-4,16,32].
2. The Standard Model and Kaluza-Klein Spacetime
The main idea behind the present strategy of calculating the dark energy is to calculate a density ratio representing the degree of emptiness or what is equivalent the sparseness of elementary messenger particles with respect to empty space [5,9]. To do this we have to quantify the relevant inherent values of particles and space. It is self-evident that the first is given directly by the number of elementary messenger particles of the standard model [5,34], while the second is slightly more involved and requires us to think deeply about the compactified dimensions of the bosonic space of the strong interactions as well as the Kaluza-Klein D = 5 unification of gravity and electromagnetism [26,27,29,30]. We start with the messenger particles of the standard model.
2.1. Lie Symmetry Groups and the Standard Model
At the time when Einstein and others considered the problems leading to the special theory of relativity around 1905 [5,35-37], nothing was then known about the elementary particles except for the electron and the photon and Maxwell’s electromagnetic field theory [5]. In the meantime we have an almost complete standard model which beside the photon (U(1)) consists of an additional eleven messenger particles, 8 Gluons for the strong force in addition to three weak force massive bosons 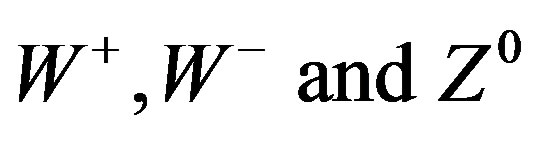 [5,9]. These particles correspond to the 11 + 1 = 12 generators of the combined Lie symmetry group of the standard model [5,9,19]
[5,9]. These particles correspond to the 11 + 1 = 12 generators of the combined Lie symmetry group of the standard model [5,9,19]
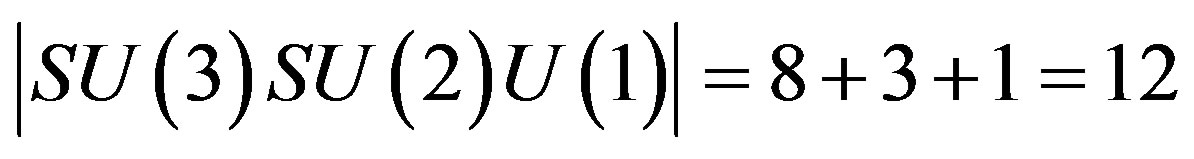 (3)
(3)
i.e., twelve massless gauge bosons [9,19].
2.2. Bosonic Strings Dimensions and Kaluza-Klein Spacetime
To unify gravity with electromagnetism [5], T. Kaluza first and O. Klein later on proposed a curved five dimensional extension of Einstein’s general relativity [26,27]. Much later the 26 dimensional bosonic string theory was developed and was motivated by the experimental success of Veneziano’s dual resonance model and Nambu strings [17]. Thus a maximum of 26 dimensions are needed and a minimum of five dimensions are required for the partial electromagnetic gravity unification [5]. The preceding information is reasonably sufficient to start our dark energy analysis.
3. Dark Energy Density in the Universe
3.1. Messenger Particles Density in D = 5 Kaluza-Klein Space
In Heterotic string theory we have 16 extra dimensions and 26 running in the opposite direction [17]. Taking out the five K-K spacetime dimensions, we are left with 16 – 5 = 11 and 26 – 5 = 21 dimensions [5,9,17,18]. We note that this eleven (11) corresponds to the 12 messenger particles of the standard model minus the single photon of U(1) involved in special relativity which is indirectly included in the Kaluza-Klein unification of gravity with electromagnetism [26,27,29]. Seen in this way, the density of the messenger particles with respect to “non-utilized space” is given approximately by [5,19]
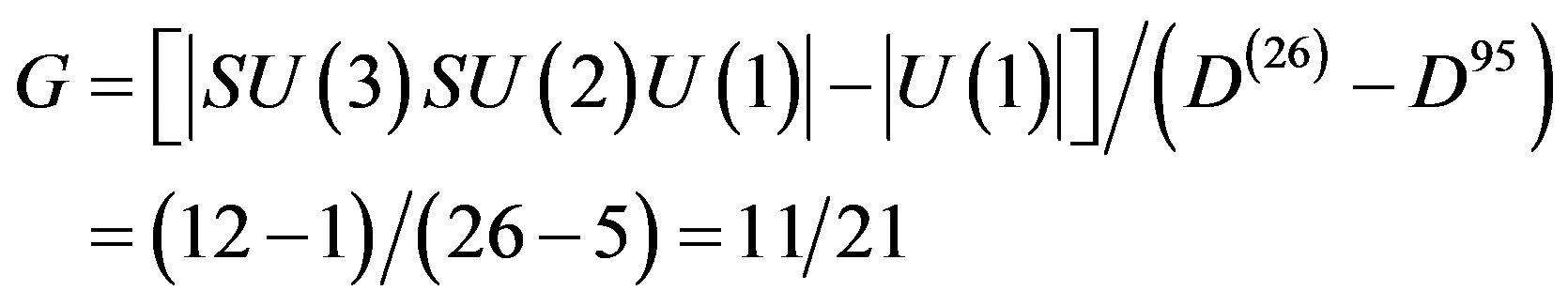 (4)
(4)
We note that this G will play a fundamental role in our analysis.
3.2. Noether’s Theorem and Lagrangian in Multiplier λ Constraint on the Energy
Noether’s theorem [5,19] shows us clearly the vital connection between symmetry, quantum particles and the conservation of energy. Thus the 12 – 1 = 11 messenger particles which are materialized by symmetry breaking bifurcation must be taken into account via the Lagrangian multiplier method to account for the constraint on energy in contrast to freely variating Newton’s kinetic energy when we let the velocity v tend to the velocity of light c. The same applies to the 26 – 5 = 21 compactified bosonic dimensions [17].
3.3. Isoperimetric Variation Function Leading to Dark Energy E(D)
Next we write down a simple energy function playing the role of a Lagrangian in terms of a state variable “a” which need not be specified for the present purpose [33]
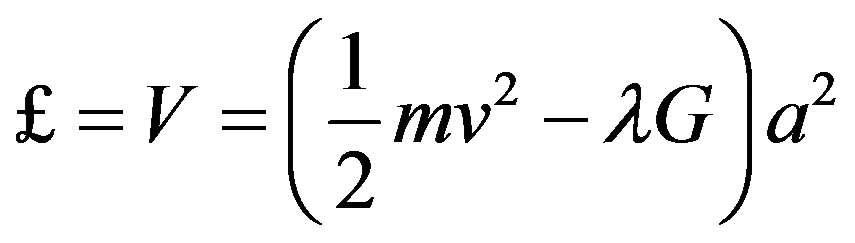 (5)
(5)
The leading positive term in the bracket is clearly nothing more than Newton’s kinetic energy while 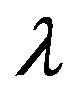 is a Lagrangian multiplier and G is the constraining auxiliary condition [33].
is a Lagrangian multiplier and G is the constraining auxiliary condition [33].
Letting the velocity 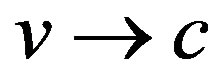 the energy function of (5) becomes
the energy function of (5) becomes
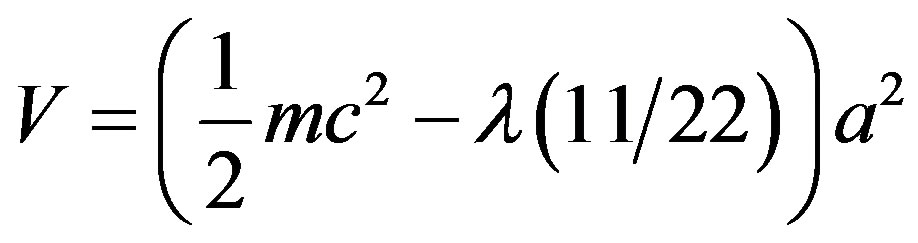 (6)
(6)
where c is the speed of light.
Finally for a stable steady state solution given by vanishing of the second variation 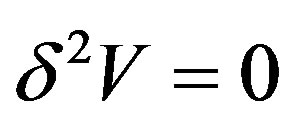 one obtains
one obtains
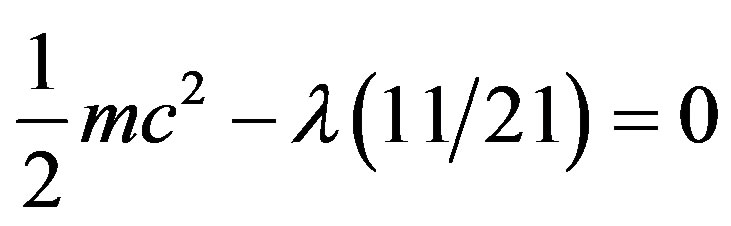 (7)
(7)
Solving for 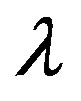 one finds
one finds
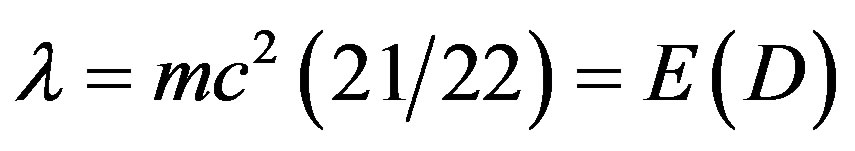 (8)
(8)
Thus dark energy is a scaling of Einstein’s famous equation 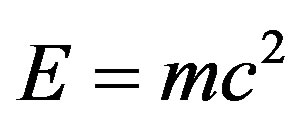 using a Weyl-Nottale scaling [7,19] exponent equal to
using a Weyl-Nottale scaling [7,19] exponent equal to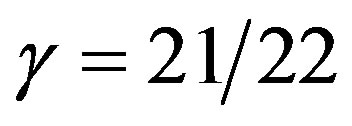 .
.
Furthermore, we gain a new and marvellous equation resulting from summing up ordinary energy E(O) and dark energy E(D) and finding Einstein’s energy
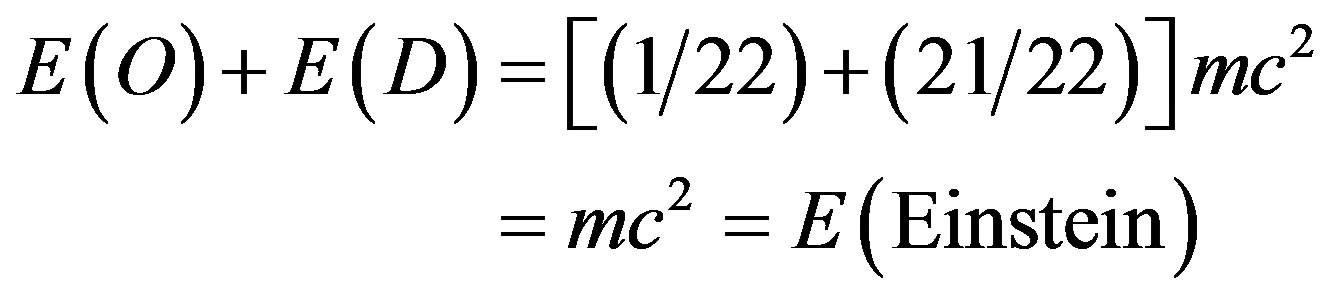 (9)
(9)
exactly as we hoped and quite honestly as we expected from the outset [9,16].
3.4. The Transfinitely Exact Analysis
To arrive at the exact expression for dark energy density which we know from the set-theoretical E-Infinity quantum mechanics to be [16,31]
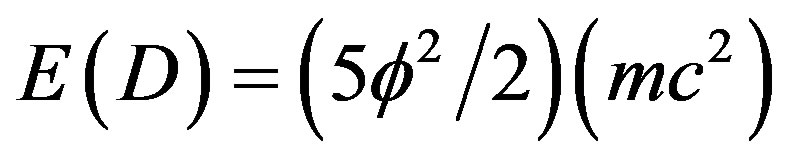 (10)
(10)
and derive this formula without resorting to our fundamental result, namely that ordinary energy is the energy of the quantum particle while dark energy is the energy of the quantum wave as per the wave-particle duality, we proceed as follows:
From fractal logic [34] we know that the fractal weight of the number of the 12 gauge bosons of the standard model is not 12 but the transfinite fuzzy value 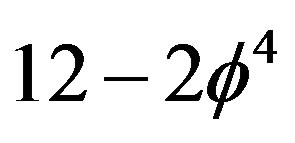 which means [19,34]
which means [19,34]
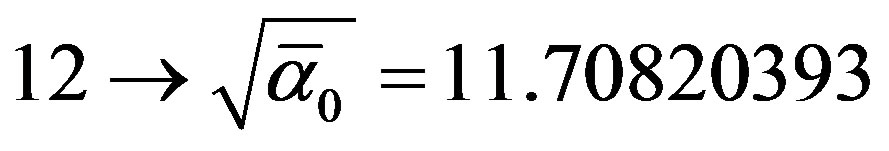 (11)
(11)
In addition the photon is given by the fractal weight number 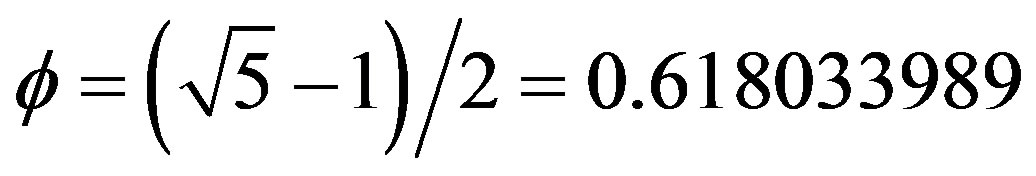 rather than the classical unity [19, 34]. Consequently one finds [34]
rather than the classical unity [19, 34]. Consequently one finds [34]
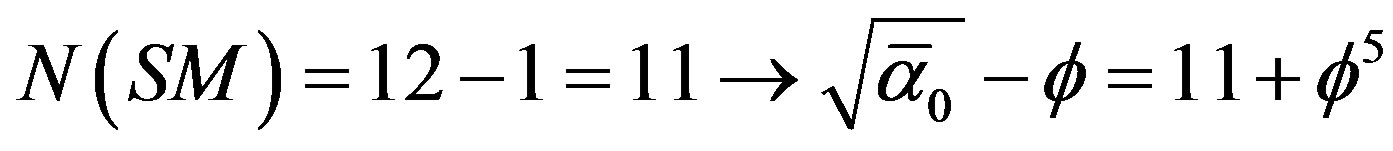 (12)
(12)
where 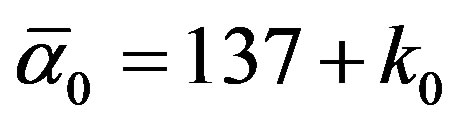 is the inverse theoretical electromagnetic fine structure constant,
is the inverse theoretical electromagnetic fine structure constant, 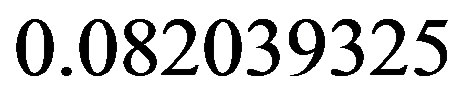
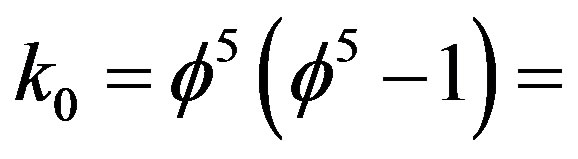 and
and 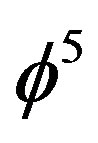 is Hardy’s probability of quantum entanglement [20,23,25]. Similarly, the 26 bosonic string dimensions are actually 26 + k where
is Hardy’s probability of quantum entanglement [20,23,25]. Similarly, the 26 bosonic string dimensions are actually 26 + k where 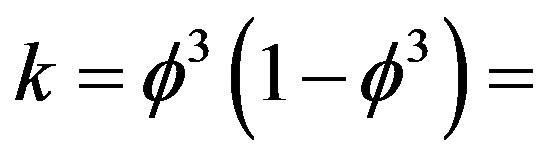
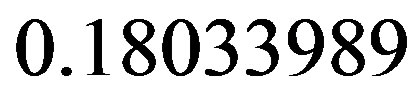 which translate to [33]
which translate to [33]
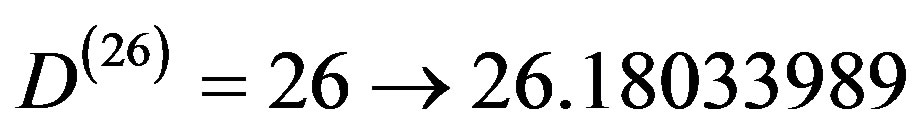 (13)
(13)
Proceeding as in the integer analysis but using our new transfinite fractal weight values, we find the corresponding Lagrangian
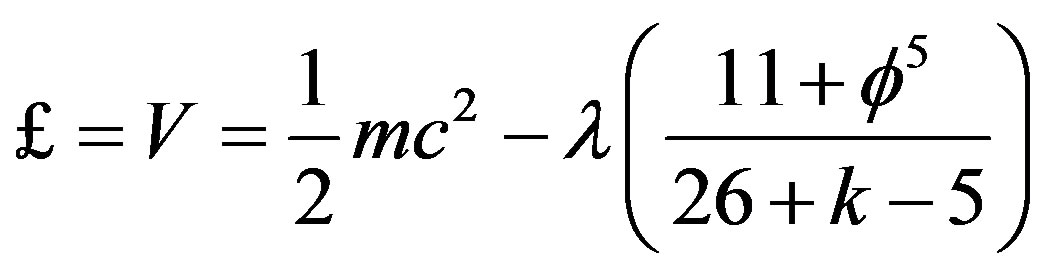 (14)
(14)
Consequently 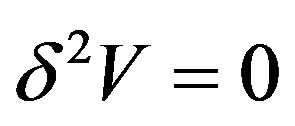 gives
gives
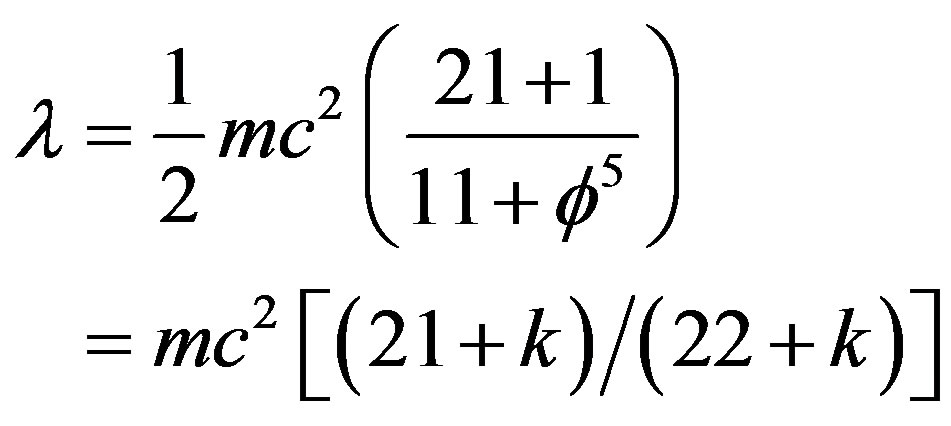 (15)
(15)
In other words the dark energy density is given by
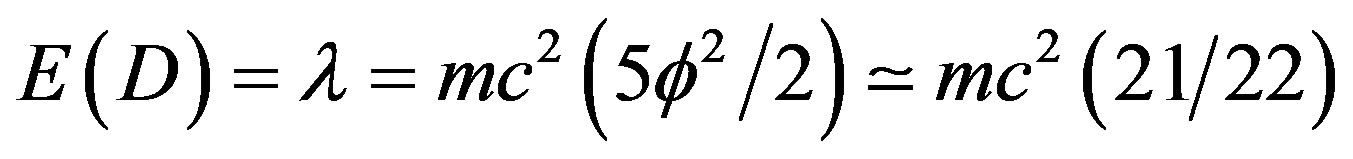 (16)
(16)
in full harmony with our previous integer approximation analysis of Section 3.3. The result given by (16) is confirmation of the fact that dark energy is the energy of the Schrödinger quantum wave [32]. This has considerable implications on both the theoretical and experimental level.
4. Conclusions
A method for determining the dark energy density of the cosmos is presented based on the concept of gauge boson density in a D = 5 Kaluza-Klein spacetime combined with 26 dimensional bosonic string space and using Noether’s theorem. It was found that the multiplier 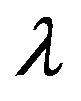 constraining the corresponding Lagrangian is equal to the dark energy density
constraining the corresponding Lagrangian is equal to the dark energy density
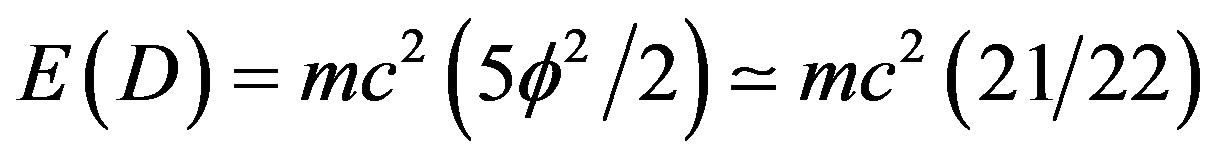 (17)
(17)
This is the complementary energy of the quantum particle and refers exclusively to the absolute value of the negative energy of the quantum wave [32]. The result is in superb agreement with the measurement executed by the research teams of the three 2011 Nobel Laureates of dark energy [1,4,11]. Finally it is vital to note that dark energy is of opposite sign to ordinary energy. Noting that ordinary energy is obviously connected to attracting gravity, it follows logically that dark energy is the cause of anti-gravity, i.e. it is behind the observed puzzling increase in the rate of cosmic expansion [1-4,10-12]. In other words 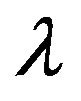 plays the role of a cosmological constant without putting anything by hand as in some alternative theories [2,3,5]. Finally we should stress that our failure to measure dark energy is basically connected to the measurement problem of quantum mechanics [5,25]. Since measurement collapses the quantum wave [5] there is currently no means for a direct measurement of the dark energy of the wave unless we find a way for a collapse free measurement. This maybe the most important lesson we could learn from the entire problem of the missing dark energy of the cosmos [1-4,9-12,16,32].
plays the role of a cosmological constant without putting anything by hand as in some alternative theories [2,3,5]. Finally we should stress that our failure to measure dark energy is basically connected to the measurement problem of quantum mechanics [5,25]. Since measurement collapses the quantum wave [5] there is currently no means for a direct measurement of the dark energy of the wave unless we find a way for a collapse free measurement. This maybe the most important lesson we could learn from the entire problem of the missing dark energy of the cosmos [1-4,9-12,16,32].
REFERENCES
- S. Perlmutter, et al., The Astrophysical Journal, Vol. 517, 1999, pp. 565-585. doi:10.1086/307221
- E. J. Copleand, M. Sami and S. Tsujikawa, “Dynamics of Dark Energy,” 2006. arxiv:hep-th/06030573.
- L. Amendola and S. Tsujikawa, Dark Energy: Theory and observations, Cambridge University Press, Cambridge. 2010. doi:10.1017/CBO9780511750823
- M. Planck, “Spacecraft,” Wikipedia, 2012.
- R. Penrose, “The Road to Reality,” Jonathan Cape, London, 2004.
- Y. Baryshev and P. Terrikorpi, “Discovery of Cosmic Fractals,” World Scientific, Singapore, 2002.
- L. Nottale, “Scale Relativity,” Imperial College Press, London, 2011.
- J. Mageuijo, “Faster than the Speed of Light,” William Heinemann, London, 2003.
- M. S. El Naschie, International Journal Modern Nonlinear Theory and Application, Vol. 2, 2013, pp. 43-54. doi:10.4236/ijmnta.2013.21005
- R. Panek, “Dark Energy: The Biggest Mystery in the Universe,” The Smithsonian Magazine, 2010. http://www.smithsonianmagazine.com/science-nature/Dark-Energy.
- E. Komatsu, et al., The Astrophysical Journal Supplement, 192, Vol. 18, 2011. arxiv: 1001.4538[astro-ph.co]
- A. G. Reiss, et al., The Astronomical Journal, Vol. 116, 1998, pp. 1009-1032.
- C. Rovelli, “Quantum Gravity,” Cambridge Press, Cambridge, 2004.
- D. R. Finkelstein, “Quantum Relativity,” Springer, Berlin, 1996. doi:10.1007/978-3-642-60936-7
- H. Saller, “Operational Quantum Theory,” Springer, Berlin, 2006.
- M. S. El Naschie, Journal of Quantum Information Science, Vol. 3, 2013, pp. 23-26. doi:10.4236/jqis.2013.31006
- J. Polchinski, “String Theory. Vol. I & II,” Cambridge University Press, Cambridge, 1998.
- M. Duff, “The World in Eleven Dimensions,” IOP Publication, Bristol, 1999.
- M. S. El Naschie, Chaos, Solitons & Fractals, Vol. 19, 2004, pp. 209-236. doi:10.1016/S0960-0779(03)00278-9
- L. Hardy, Physical Review Letters, Vol. 7, 1993, pp. 1665-1668. doi:10.1103/PhysRevLett.71.1665
- D. F. Styer, “The Strange World of Quantum Mechanics,” Cambridge University Press, Cambridge, 2000, pp. 54-55.
- J. Mageuijo and L. Smolin, “Lorenz Invariance with an Invariant Energy Scale,” 18 December 2001. Arxiv: hep.th/0112090v2
- D. Mermin, American Journal of Physics, Vol. 62, 1999, pp. 880-887. doi:10.1119/1.17733
- P. Davis, “The New Physics,” Cambridge University Press, Cambridge, 1989.
- M. S. El Naschie Journal of Quantum Information Science, Vol. 1, 2011, pp. 50-53. doi:10.4236/jqis.2011.12007
- P. Halpern, “The Great beyond, Higher Dimensions, Parallel Universes and the Extraordinary Search for a Theory of Everything,” John Wiley, New Jersey, 2004.
- M. S. El Naschie, Chaos, Solitons & Fractals, Vol. 37, 2008, pp. 16-22. doi:10.1016/j.chaos.2007.09.079
- A. Connes, “Non-Commutative Geometry,” Academic Press, New York, 1994, pp. 88-93.
- M. S. El Naschie, Chaos, Solitons & Fractals, Vol. 26, 2005, pp. 247-254. doi:10.1016/j.chaos.2005.01.016
- M. S. El Naschie, Chaos, Solitons & Fractals, Vol. 36, 2009, pp. 808-810. doi:10.1016/j.chaos.2007.09.019
- J. H. He, International Journal of Modern Nonlinear Theory and Application, Vol. 2, 2013, pp. 55-59. doi:10.4236/ijmnta.2013.21006
- L. Marek-Crnjac, et al., International Journal of Modern Nonlinear Theory and Application, Vol. 2, 2013, pp. 78- 88. doi:10.4236/ijmnta.2013.21A010
- C. Lanzos, “The Variational Principles of Mechanics,” 4th Edition, University of Toronto Press, Toronto, 1949.
- M. S. El Naschie, International Journal of Modern Nonlinear Theory and Application, Vol. 1, 2012, pp. 84-92. doi:10.4236/ijmnta.2012.13012
- W. Rindler, “Relativity,” Oxford University Press, Oxford, 2001.
- J. Hsu and L. Hsu, “A Broader View of Relativity,” World Scientific, Singapore, 2006.
- J. Hartle, “Gravity,” Addison Wesley, New York, 2003.

