Journal of Modern Physics
Vol.4 No.5(2013), Article ID:31594,7 pages DOI:10.4236/jmp.2013.45085
Extra Dimensions Corrections for Fermionic Casimir Effect in Three Dimensional Box
Theoretical Physics and Natural Philosophy Laboratorium, Sepuluh Nopember Institute of Technology, Surabaya, Indonesia
Email: herusukamto@physics.its.ac.id, purwanto@physics.its.ac.id
Copyright © 2013 Heru Sukamto, Agus Purwanto. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 27, 2013; revised March 28, 2013; accepted April 25, 2013
Keywords: Casimir; Fermionic; Extra Dimensions
ABSTRACT
We want to show extra-dimensions corrections for Fermionic Casimir Effect. Firstly, we determined quantization fermion field in Three dimensional Box. Then we calculated the Casimir energy for massless fermionic field confined inside a three-dimensional rectangular box with one compact extra-dimension. We use the MIT bag model boundary condition for the confinement and M4 × S1 as the background spacetime. We use the direct mode summation method along with the Abel-Plana formula to compute the Casimir energy. We show analytically the extra-dimension corrections to the Fermionic Casimir effect to forward a new method of exploring the existence of the extra dimensions of the universe.
1. Introduction
Casimir effects, first discovered in 1948 [1], are manifestation of the zero-point energies of the quantum fields and have played an important role on a variety of fields of physics. It discovered by Hendrick Casimir. He showed that zero-point fluctuations in electromagnetic fields gave rise to an attractive force between parallel, perfectly conducting plates. Since spacetimes with extra dimensions are fundamental in most of theories of high energy physics, there have been intensive activities in investigating the Casimir effect in spacetime with extra dimensions. The case of a scalar field and electromagnetic field with various boundary conditions has been studied at either zero or finite temperature, for different extra-dimensional spacetimes such as Kaluza-Klein spacetime and RandallSundrum spacetime [2-3]. For fermionic field, there has been calculated Casimir energy in three-dimensional box [4]. There also has been calculated Casimir energy between parallel plates with compact dimensions [5]. Then, in this paper we investigate the extra-dimension correction to fermionic Casimir energy in three-dimensional box to explore the existence of extra-dimensions of our universe.
This article is organized as follows: In Section 2 we present the solution to the Dirac equation in 5D subject to the MIT bag model boundary condition in all the surfaces. Then we compute the Casimir energy by performing a direct sum over all modes of the field using the Abel-Plana summation formula. As we shall show, there will be no need for any analytic continuation techniques in this case. There will be influenced from extra dimension on the nature of Casimir energy between the configuration boundary that confine the field in the spacetimes with extra dimensions.
2. The Dirac Field 5D Confined in Three-Dimensional Cube
We consider a quantum fermionic field  on (3 + 1 + 1)-dimensional spacetimes with
on (3 + 1 + 1)-dimensional spacetimes with 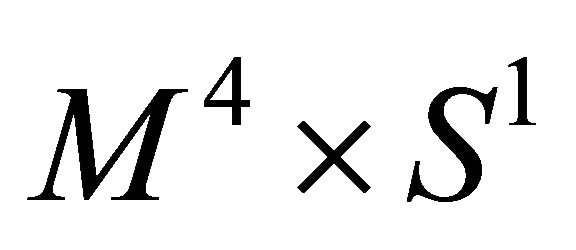 manifold.
manifold.
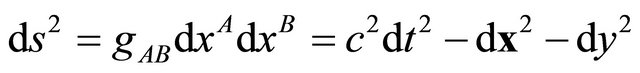 (1)
(1)
The field  is assumed to satisfy the general compactification
is assumed to satisfy the general compactification
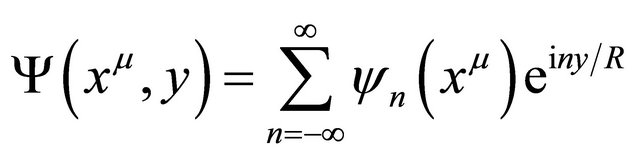 (2)
(2)
where R is the size of extra dimension. The field Ψ satisfy 5D Dirac equation
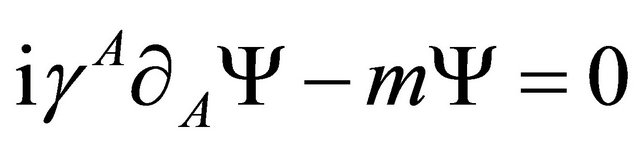 (3)
(3)
using the chiral representation of Dirac matrices
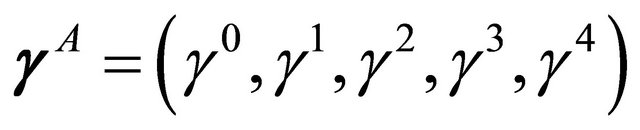 (4)
(4)
with 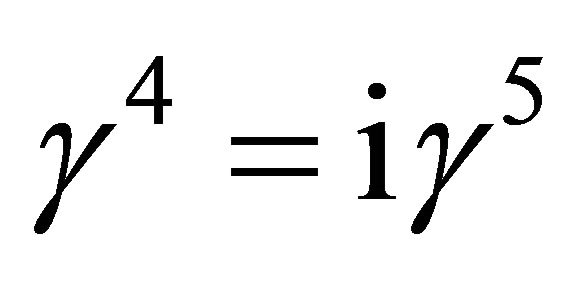 [6]. The positive energy solution of the 5D Dirac equation can be written respectively as
[6]. The positive energy solution of the 5D Dirac equation can be written respectively as
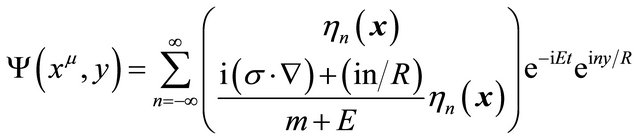 (5)
(5)
Spinor 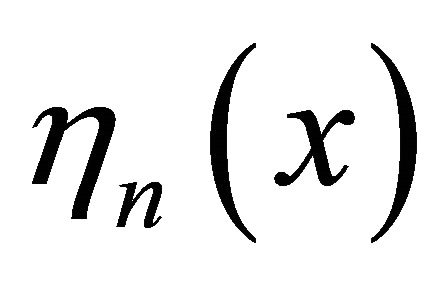 are given by
are given by
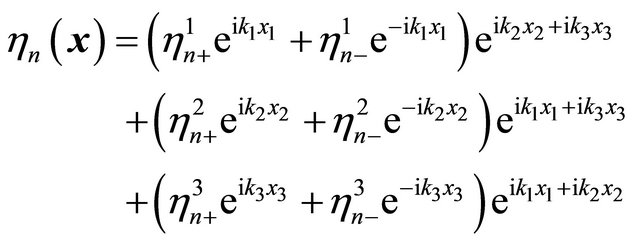 (6)
(6)
Then we have
 (7)
(7)
The MIT bag model boundary condition is usually said to imply that there is no flux of fermions through the boundary. The prevalent form of the MIT bag model boundary condition is as follows:
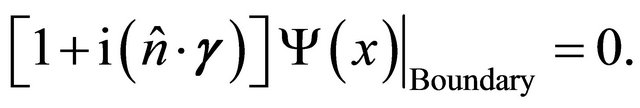 (8)
(8)
This boundary condition for our special case becomes
 (9)
(9)
where 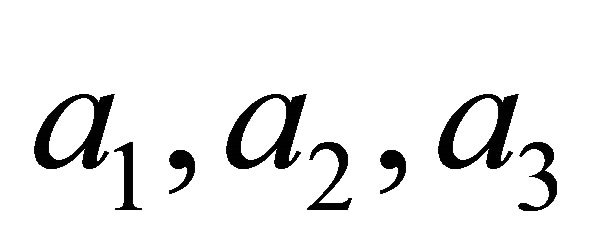 denote the lengths of the sides of the box. Subtituting Equations (6) and (7) into Equation (9) we obtain, for example, the following two equation for
denote the lengths of the sides of the box. Subtituting Equations (6) and (7) into Equation (9) we obtain, for example, the following two equation for  surface:
surface:
 (10)
(10)
for , we get
, we get
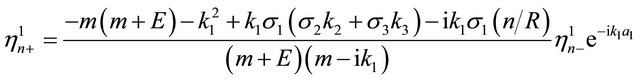 (11)
(11)
and for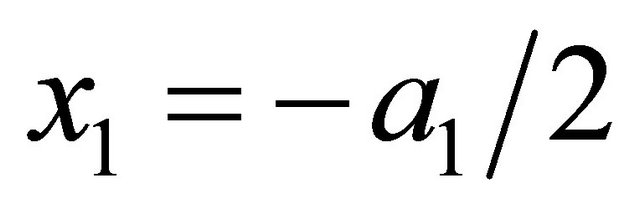 , we get
, we get
 (12)
(12)
Comparing (11) with (12), we find that in order to have nontrivial solutions for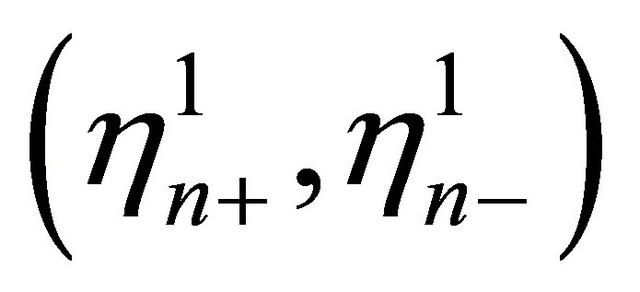 , one requires k1 to satisfy a transcendental equation
, one requires k1 to satisfy a transcendental equation
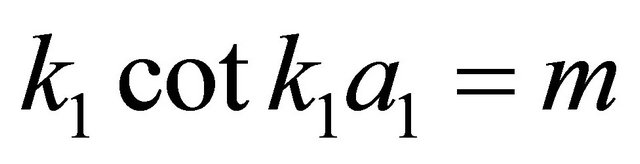 (13)
(13)
by setting 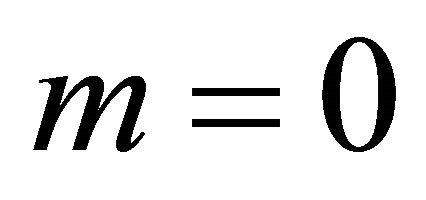 for massless Dirac field, the quantization condition Equation (13) yields
for massless Dirac field, the quantization condition Equation (13) yields
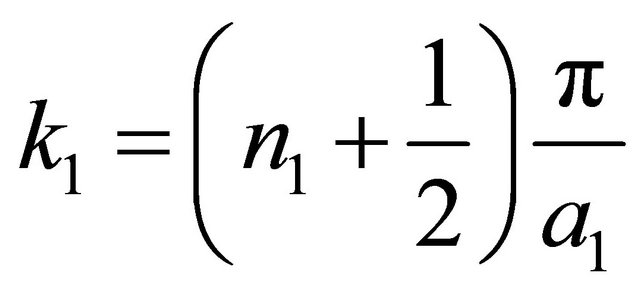 (14)
(14)
3. Casimir Fermionic Energy in Three-Dimensional Cube at M4 × S1
From this point, we concentrate on the massless case with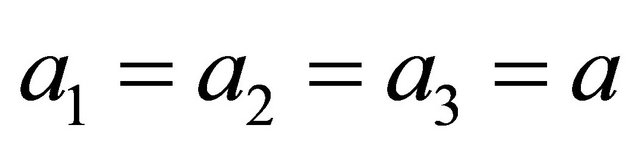 , for simplicity. By using the second quantized form of Dirac field, the vacuum expectation value of the free Hamiltonian can be expressed in the form
, for simplicity. By using the second quantized form of Dirac field, the vacuum expectation value of the free Hamiltonian can be expressed in the form
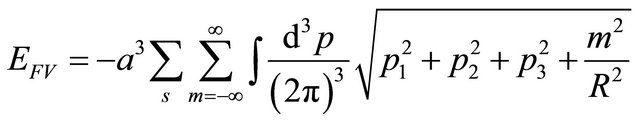 (15)
(15)
where summation index runs over the spin states and subscripts FV stands for free vacuum. In the presence of the boundaries, all of components of the momentum are subjected to quantization condition Equation (14). Therefore the integrals turn into summations:
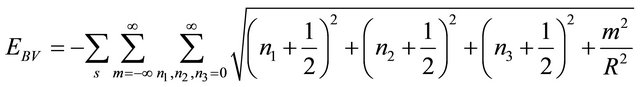 (16)
(16)
where EBV denotes the vacuum energy in the presence of the boundaries. Obviously, in both situations the vacuum energy is divergent. However, the Casimir energy, which is the difference between these two quantities, is usually expected to be finite. One usually needs to utilize a regulation prescription to give a physical meaning to such a difference. In this paper we choose a modified form of the Abel-Plana formula, which is useful for the summation over half-integer numbers
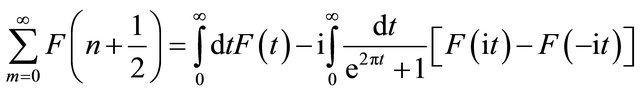 (17)
(17)
where F(z) is assumed to be an analytic function in the right half-plane. The first term is the main term of turning a sum into an integral. The second term is called branchcut term. Since we have a four sum over for Equation (16), we need to apply the Abel-Plana formula four times. The details are given in the Appendix. The final result is
 (18)
(18)
with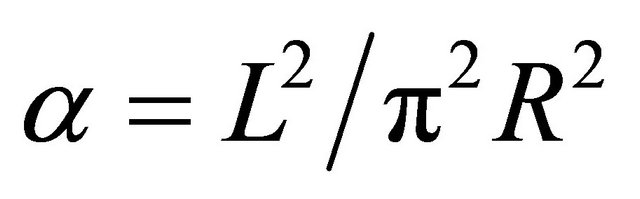 . It is extremely important to note that the only divergent quantity in Equation (18) is the first term, which is precisely the free vacuum energy
. It is extremely important to note that the only divergent quantity in Equation (18) is the first term, which is precisely the free vacuum energy 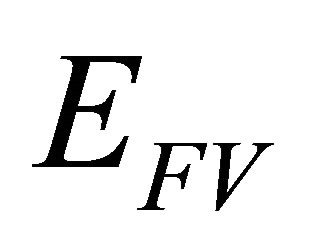 and is supposed to be subtracted from
and is supposed to be subtracted from  in order to obtain the Casimir energy. Second, fourth, and fifth term related to extra dimension corrections.
in order to obtain the Casimir energy. Second, fourth, and fifth term related to extra dimension corrections.
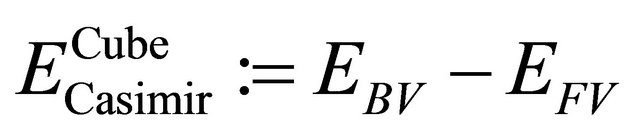 (19)
(19)
As a check on our procedure we have computed the Casimir energy for a fermionic field between two parallel plates in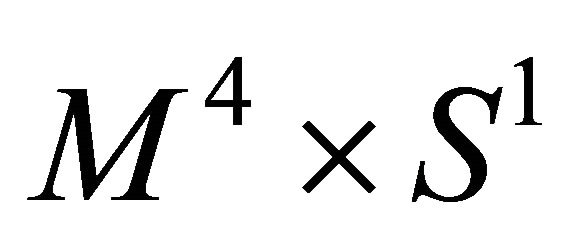 , separated by a distance a, and extradimensional size R, we obtain
, separated by a distance a, and extradimensional size R, we obtain
 (20)
(20)
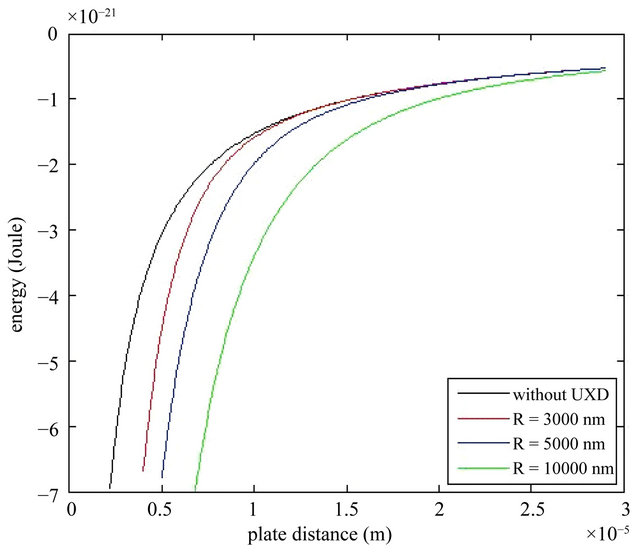
Figure 1. Fermionic Casimir energy with and without a compact dimension as a function of the plates separation.
Figure 1 depicts the dependence of the Fermionic Casimir energy in a Three-dimensional box on a radius of extra dimension and the size of the box. It is showed that corrections’ factors increase proportional to the size of extra dimensions. For extra dimension correction, we deduce from Equation (20) that

If there are no extra dimension, then the term αm2 vanishes. Then casimir energy will become as be shown by [4].
4. Conclusion
In this paper, we have investigated the extra dimensional corrections for Casimir energy in a three-dimensional box in 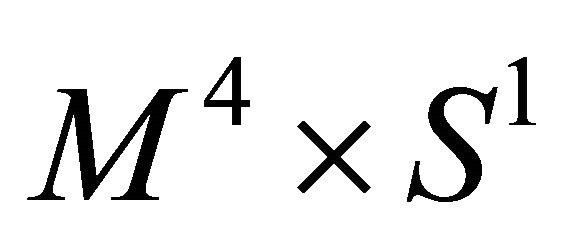 due to the vacuum fluctuations of massless fermionic field with MIT bag boundary conditions. The Casimir energy is computed using generalized AbelPlana summation formula. The most important result we obtain in this letter is that Fermionic Casimir energy depends on the size of extra dimensions.
due to the vacuum fluctuations of massless fermionic field with MIT bag boundary conditions. The Casimir energy is computed using generalized AbelPlana summation formula. The most important result we obtain in this letter is that Fermionic Casimir energy depends on the size of extra dimensions.
REFERENCES
- H. B. G. Casimir, Koninklijke Nederlandse Akademie van Wetenschappen, Vol. 51, 1948, p. 793
- K. A. Milton, “The Casimir Effect: Physical Manifestations of Zero-Point Energy,” World Scientific, River Edge, 2001.
- L. P. Theo, “Casimir Effect in Spacetime with Extra Dimensions-From Kaluza-Klein to Randall Sundrum Models.” ArXiv:hep-th/0907.2989v3
- A. Seyedzahedi, R. Saghian and S. S. Gousheh, Physical Review A, Vol. 82, 2010, Article ID: 032517. http://dx.doi.org/10.1103/PhysRevA.82.032517
- F. S. Khoo and L. P. Theo, Physics Letters B, Vol. 703, 2011, pp. 199-207. http://dx.doi.org/10.1016/j.physletb.2011.07.072
- P. Alejandro Sanchez, M. Anabitarte and M. Bellini, “Dirac Equation in a de Sitter Expansion for Massive Neutrinos from Modern Kaluza-Klein Theory,” 2012. ArXiv:hep-th/1112.5183v4
- K. Poppenhaeger, S. Hossenfelder, S. Hosmann and M. Bleicher, “The Casimir Effect in the Presence of Compactified Universal Extra Dimensions,” 2003. ArXiv:hep-th/0309066v2
Appendix: Abel-Plana Formula in Calculating the Casimir Energy
In this appendix we present the details of the calculations leading to our main expression for the casimir energy of a massless fermionic field confined inside cube with one extra dimension via MIT bag model boundary condition. In order to apply the Abel-Plana formula to four sum in Equation (16), we first define
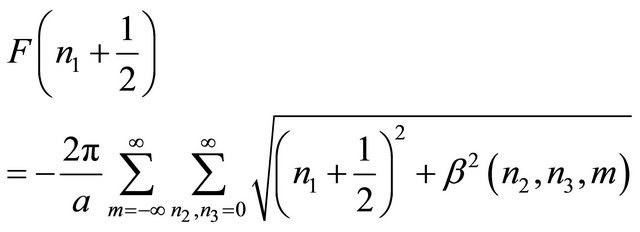 (A1)
(A1)
with
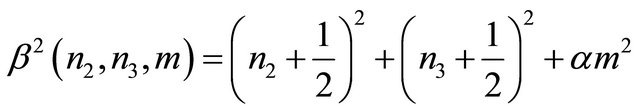
The factor 2 is associated with the spin multiplicity. The branch-cut term can be calculated using the following:
 (A2)
(A2)
By using Equations (17) and (A2), Equation (16) turns into
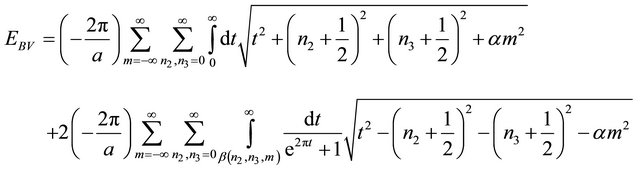 (A3)
(A3)
The first term is infinite and we have to use the Abel-Plana formula again for the first term. We obtain
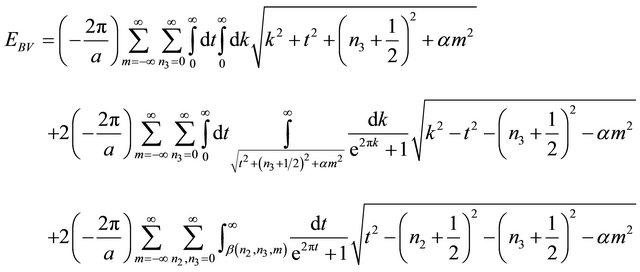 (A4)
(A4)
Again the first term is infinite and we must apply the Abel-Plana formula to obtain
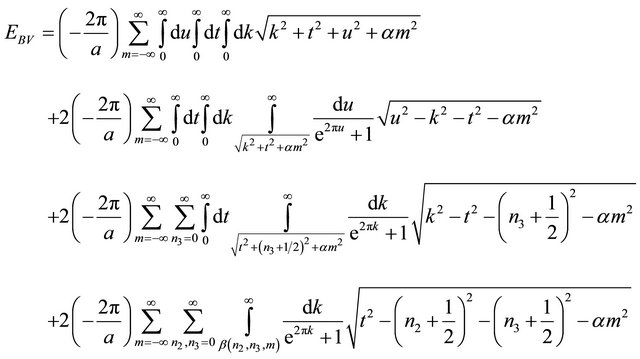 (A5)
(A5)
Note that all of branch cut terms is finite. On other hand the free vacuum energy is
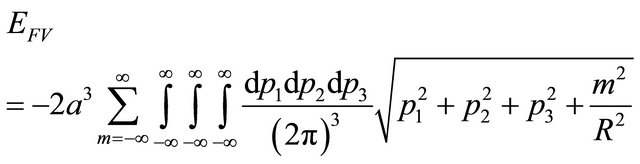 (A6)
(A6)
Making appropriate changes of variables, we obtain
 (A7)
(A7)
Therefore when we compute the Casimir energy these two terms precisely cancel each other. That is,
 (A8)
(A8)
here we explain the details of the calculation of the last term and then outline the calculation for remaining terms. We expand the denominator as follows:
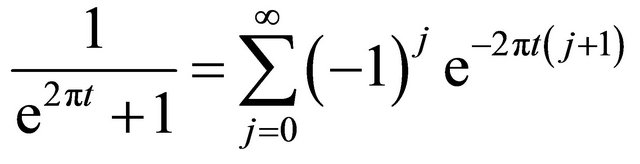 (A9)
(A9)
The last term turn into
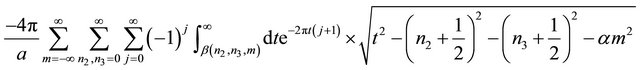 (A10)
(A10)
by using the identity
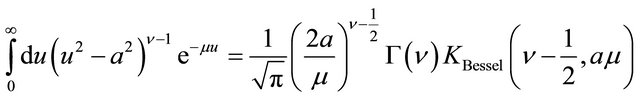 (A11)
(A11)
then we have
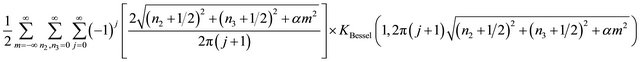 (A12)
(A12)
In order to compute the second term of Equation (A8) we first interchange the order of integrations to obtain
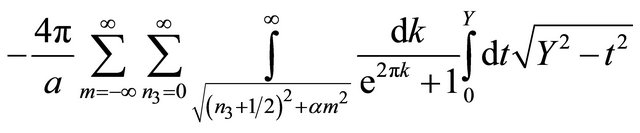 (A13)
(A13)
where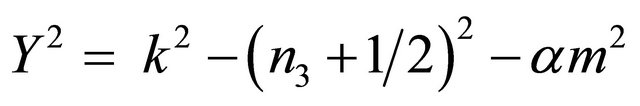 . Now using Equations (A9) and (A11) we obtain
. Now using Equations (A9) and (A11) we obtain
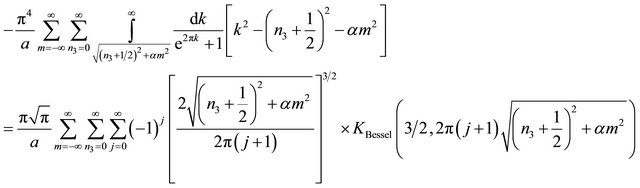 (A14)
(A14)
Going through this same procedure, we can compute the first branch-cut term in Equation (A8) as follows:
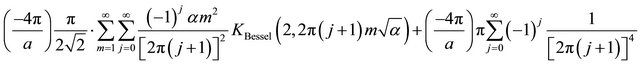 (A15)
(A15)
Finally, we arrive at
 (A16)
(A16)

