Journal of Modern Physics
Vol.4 No.3A(2013), Article ID:29352,4 pages DOI:10.4236/jmp.2013.43A061
Stair Magnetism: Distinct Magnetic States of Co5C5 Carbide Isomers
ATG:biosynthetics, Merzhausen, Germany
Email: kuznet61@gmail.com
Received October 22, 2012; revised November 22, 2012; accepted December 2, 2012
Keywords: The Metal Cluster; Carbon Shell; Magnetization; Emergence of Atypical Properties
ABSTRACT
Ruffle magnetic landscape of transition metals (TM) is a trouble of material science that makes it hard to predict properties of nanomagnets [1,2]. It is not quite clear, whether jumps in magnetic activity is the intrinsic property of TM complexes or a controversy of computational experiments. To solve this problem, isomers of Co5C5 carbide with various positions of carbon atoms on the vertices of Co5 cluster were investigated in DFT (Density Functional Theory) computer simulations. It was found that magnetic moments of the carbide isomers increased with the decreasing number of Co–C bonds. However, C-2 isomers have three Co–C bonds demonstrated distinctive magnetic states. The Co5C5 carbide system showed a discrete magnetism. It was supposed that similar magnetic arrangements take place in endohedral metallofullerenes and filled nanotubes.
1. Introduction
Interaction of transition metals (TM) with carbon atoms [3,4] is a significant interest for material science because the contact between Meand C-atoms can affect electronic properties of metals, in particular their magnetic characteristics [5]. Even this kind of interaction could lead to a new property of a whole metal-carbon complex [6].
Several papers were recently published on the putative endohedral metallofullerenes Men@Cm obtained by an encapsulation of transition-metal clusters (Fe, Co, Ni, Tc, n = 2 - 7) into carbon fullerenes (m = 60, 70, 80, 82, 90) in the frame of quantum mechanical simulations employing Density Functional Theory (DFT) [2,7-9]. The “encapsulation” means the merging of available or previously calculated atomic coordinates for the TM cluster and the fullerene with the following structural optimization and prediction of physical characteristics. Those reports presented rough magnetic plots for fullerenes with introduced metal clusters of increasing size. I called this phenomenon “Dragon’s Teeth (DT) problem”. This effect is not restricted only by metallofullerenes. For example, the DFT study on binding of Co clusters (n = 2 - 19) with chitosan molecules demonstrated an even more ruffle magnetic landscape [10], which caused me to think about the DT-problem.
Following those experiments, I investigated carbides in addition to metallofullerenes [11,12] to distinguish the effects of exchange-correlation functionals in DFT, as well as the efficiency of structural relaxation to ground state, and the role of carbon atoms covering a magnetic cluster. To be mentioned, it was demonstrated before that there is no difference in usage between Perdew and Wang (PW91) as well as Perdew, Burke, and Ernzerhof (PBE) functionals in case Tcn@C60 (n = 2 - 7) complexes [7]. In my own experiments, the local density (LDA) and generalized gradient (GGA) approximations yield similar results for carbides and endohedral metalofullerenes on the basis of Co5 and Co13 clusters. The gradient and subspace optimization methods did not always allow reaching a ground state, rather than that they finished sometimes at local minima in case of large Co13 systems [11]. The data obtained from Co5 systems allowed me to report on the reduction of magnetism for cobalt clusters encapsulated in fullerenes [12]. As was shown, the magnetic moment of a metallofullerene depended on the orientation of metal cluster in fullerene, particularly on the distances between Cand Me-atoms. That gave me a possibility to speculate upon the role of Me-C binding in the spin-orbit coupling between electrons, leading to a silencing of the total spin magnetic moment for the Me-C complex. Nevertheless, the “ruffle” magnetism of metallofullerenes as a result of possible emergent effect is still a puzzle.
To decompose the problem, I supposed that a small TM cluster covered by few C-atoms could mimic a behavior of the same cluster inserted in a fullerene. A simple model of the Co5 metallic cluster covered by five carbon atoms in various positions was used to demonstrate discrete magnetic properties of Co5C5 carbide isomers that may clear up the DT-problem.
2. Experimental Procedure
The Co5 cluster was enclosed by carbons using Avogadro v.1.0 software [13]. Density Functional Theory [14] was implemented within the OpenMX v.3.5 code [15-18]. The calculation was made using the generalized gradient approximation of Perdew-Burke-Ernzerhof (GGA-PBE) [19] with parameters fitted to d-orbitals of Co-atoms. Structural relaxation was performed by direct inversion iterative sub-space optimization (DIIS) [20]. The atomic species were defined as C4.0-s1p1 and Co5.5-s2p2d2f1 [21] with energy cutoff 200.0 Ryd. The energy convergence criterion (SCF) was set to 1.0e−6 Hartree, electronic temperature was 300.0 K.
3. Results and Discussion
Table 1 shows twelve isomers of Co5C5 carbide divided into two groups depending on the arrangements of carbon atoms at the apexes (a) or at the equator (b) of the trigonal bipyramid Co5 cluster.
From Figure 1, one finds a trend of the increasing magnetic moment with the reducing number of Co–C bonds in the investigated compounds. The fully carbon covered C-0 compound demonstrated 23.08% of the magnetic activity of a reference, i.e. the pure Co5 cluster. Reducing the number of the Co–C bonds led to 38.48% for C-1 compounds on the one hand and in general to 84.62% for C-3 and C-4 compounds on the other side of the progression.
That is interesting, the magnetism changed not monotonically nor smoothly, but particularly stepwise like a stair with about 15.4% discrepancy between each of six separate magnetic states. I found that isomers of C-2 compound with two reduced Co–C bonds can occupy the three different magnetic levels, such as about 53.79%, 69.25% and 84.62% of initial activity of the pure cobalt cluster.
The most interesting isomer b-C-2”, with two reduced apical Co–C bonds and carbon atoms disposed near the
Table 1. Examples of Co5C5 carbide isomers with magnetism related to pure Co5 cluster (%).
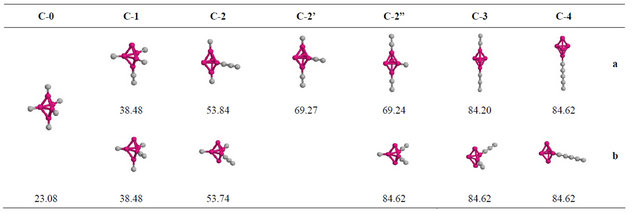
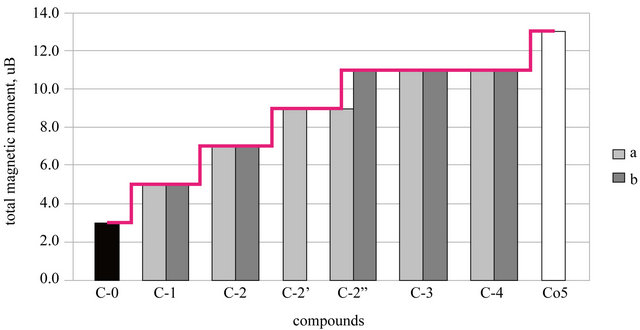
Figure 1. Total spin magnetic moments of Co5C5 carbide isomers (µB).
equator, demonstrated “atypical” high magnetic activity similar to C-3 and C-4 compounds with reduced three and four Co–C bonds, respectively.
It should be pointed out that the rough “Dragon’s Teeth” appeared in calculations of spin magnetic moments of covered metal clusters via both VASP [2,7] and OpenMX [8,9] software, as well as LDA + U [10], GGAPW91 [7], or GGA-PBE [2,7-9] functionals. Vienna ab initio Simulation Package (VASP) using the projector augmented wave (PAW) method is one of the most accurate packages, which is also considered as a state of the art in DFT codes [22-25]. OpenMX’s basis set is mainly designed to simulate large systems [15-17], but its basis set is less accurate than the plane-wave basis set in PAW method, which is implemented in VASP. A priori, VASP code would be more correct than OpenMX code for small systems like small magnetic clusters. However, this difference was not apparent in computational experiments on metallofullerenes. Both kind of code generated similar “Dragon’s Teeth” within various approximations.
To avoid the DT-problem in earlier experiments [11, 12], I carefully planned the experimental set of metal clusters and carbon fullerenes. Unambiguous results were obtained on alternative orientations of the same cluster in the same fullerene cage [12]. Functional dependence of magnetism on average Me–C distances and number of Me–C bonds was found [11]. I also observed “smooth” suppression of magnetism for carbides with an increasing number of covering C-atoms. Nevertheless, as we can see now, I lost evidences about quantum magnetism. It should be mentioned that Ni-atom clusters (n = 2 - 6) demonstrated the similar stair magnetic trend in a gas phase and in fullerene cages (m = 60, 70, 80, 90), however, authors did not emphasize this interesting fact [2].
4. Conclusion
The set of Co5C5 carbide isomers allowed me to shed light on the “Dragon’s Teeth” problem. From the experiment presented here it follows that the C-2 isomers with the same number of Co–C bonds showed distinctive magnetic moments depending on the arrangements between cobalt and carbon atoms. This control setup demonstrated the quantum feature of magnetism at atomic level and the absence of injective relations between isomer conformations and magnetic states. Thus, I suspect even more sophisticated behavior in magnetisation of complex systems like fullerenes and nanotubes by doping magnetic clusters. It will be interesting to see if the same features are found in real nanomagnets.
5. Acknowledgements
I would like to express many thanks to Heinz Eikmeyer and anonymous referees for suggestions.
REFERENCES
- I. Garg, H. Sharma, N. Kapila, K. Dharamvir and V. K. Jindal, “Transition Metal Induced Magnetism in Smaller Fullerenes (Cn for n ≤ 36),” Nanoscale, Vol. 3, No. 1, 2011, pp. 217-224. doi:10.1039/c0nr00475h
- P. Tereshchuk and J. L. F. Da Silva, “Encapsulation of Small Magnetic Clusters in Fullerene Cages: A Density Functional Theory Investigation within van der Waals Corrections,” Physical Review B, Vol. 85, No. 19, 2012, Article ID: 195461. doi:10.1103/PhysRevB.85.195461
- B. I. Swanson, S. I. Hamburg and R. R. Ryan, “Bonding in Divalent Transition Metal Cyanides. Crystal Structure of Dicesium Magnesium Hexacyanoferrate (II),” Inorganic Chemistry, Vol. 13, No. 7, 1974, pp 1685-1687. doi:10.1021/ic50137a028
- E. A. Robinson, “Interpretation of Bond-Length Data for Transition-Metal-Acetylene Complexes, in Particular the Complex [C5H5NH][TaCI,(PhC=CPh)(NC5H5)],” Journal of the Chemical Society, Dalton Transactions, No. 12, 1981, pp. 2373-2375. doi:10.1039/dt9810002373
- P. Susmita, Ch. Sayan, Ph. Manh-Huong, M. Pritish and S. Hariharan, “Carbon Nano Straws: Nanotubes Filled with Superparamagnetic Nanoparticles,” Nanotechnology, Vol. 20, No. 48, 2009, Article ID: 485604. doi:10.1088/0957-4484/20/48/485604
- C. Soldano, F. Rossella, V. Bellani, S. Giudicatti and S. Kar, “Cobalt Nanocluster-Filled Carbon Nanotube Arrays: Engineered Photonic Bandgap and Optical Reflectivity,” ACS Nano, Vol. 4, No. 11, 2010, pp. 6573-6578. doi:10.1021/nn101801y
- P. F. Weck, E. Kim, K. R. Czerwinski and D. Tomanek, “Structural and Magnetic Properties of Tcn@C60 Endohedral Metalofullerenes: First-Principles Predictions,” Physical Review B, Vol. 81, No. 12, 2010, Article ID: 125448. doi:10.1103/PhysRevB.81.125448
- M. B. Javan, N. Tajabor, M. Rezaee-Roknabadi and M. Behdani, “First Principles Study of Small Cobalt Clusters Encapsulated in C60 and C82 Spherical Nanocages,” Applied Surface Science, Vol. 257, No. 17, 2011, pp. 7586-7591. doi:10.1016/j.apsusc.2011.03.132
- M. B. Javan and N. Tajabor, “Structural, Electronic and Magnetic Properties of Fen@C60 and Fen@C80 (n = 2 - 7) Endohedral Metallofullerene Nano-Cages: First Principles Study,” Journal of Magnetism and Magnetic Materials, Vol. 324, No. 1, 2012, pp. 52-59. doi:10.1016/j.jmmm.2011.07.034
- P. L. Tereshchuk, “Energetic and Magnetic Properties of Chitosan with Embedded Co Clusters,” Computational Materials Science, Vol. 50, No. 3, 2011, pp. 991-997. doi:10.1016/j.commatsci.2010.10.038
- A. Kuznetsov, “From Carbides to Co5 and Co13 Metallofullerenes: First-Principles Study and Design,” American Journal of Biomedical Engineering, Vol. 2, No. 1, 2012, pp. 32-38. doi:10.5923/j.ajbe.20120201.05
- A. Kuznetsov, “Magnetic Properties of Endohedral Complexes Co5@Cn Depending upon the Size and Symmetry of Fullerenes as well as Orientation of Cobalt Cluster,” Computational Materials Science, Vol. 54, 2012, pp. 204- 207. doi:10.1016/j.commatsci.2011.09.034
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, “Visualization, and Analysis Platform,” Journal of Cheminformatics, Vol. 4, 2012, pp. 1-17. http://www.jcheminf.com/content/4/1/17 doi:10.1186/1758-2946-4-17
- P. Hohenberg and W. Kohn, “Inhomogeneous Electron Gas,” Physical Review B, Vol. 136, No. 3B, 1964, pp. B864-B871. doi:10.1103/PhysRev.136.B864
- T. Ozaki, “Variationally Optimized Atomic Orbitals for Large-Scale Electronic Structures,” Physical Review B, Vol. 67, No. 15, 2003, Article ID: 155108. doi:10.1103/PhysRevB.67.155108
- T. Ozaki and H. Kino, “Numerical Atomic Basis Orbitals from H to Kr,” Physical Review B, Vol. 69, No. 19, 2004, Article ID: 195113. doi:10.1103/PhysRevB.69.195113
- T. Ozaki and H. Kino, “Efficient Projector Expansion for the ab Initio LCAO Method,” Physical Review B, Vol. 72, No. 4, 2005, Article ID: 045121. doi:10.1103/PhysRevB.72.045121
- OpenMX, http://www.openmx-square.org/
- P. Perdew, K. Burke and M. Ernzerhof, “Generalized Gradient Approximation Made Simple,” Physical Review Letters, Vol. 77, No. 18, 1996. pp. 3865-3868. doi:10.1103/PhysRevLett.77.3865
- P. Császár and P. Pulay, “Geometry Optimization by Direct Inversion in the Iterative Subspace,” Journal of Molecular Structure, Vol. 114, 1984, pp. 31-34. doi:10.1016/S0022-2860(84)87198-7
- http://www.jaist.ac.jp/~t-ozaki/vps_pao2006/vps_pao.html
- G. Kresse and J. Hafner, “Ab Initio Molecular Dynamics for Open-Shell Transition Metals,” Physical Review B, Vol. 48, No. 17, 1993, pp. 13115-13118. doi:10.1103/PhysRevB.48.13115
- G. Kresse and J. Furthmüller, “Efficient Iterative Schemes for ab Initio Total-Energy Calculations Using a PlaneWave Basis Set,” Physical Review B, Vol. 54, No. 16, 1996, pp. 11169-11186. doi:10.1103/PhysRevB.54.11169
- E. Blöchl, “Projector Augmented-Wave Method,” Physical Review B, Vol. 50, No. 24, 1994, pp. 17953-17979. doi:10.1103/PhysRevB.50.17953
- G. Kresse and D. Joubert, “From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method,” Physical Review B, Vol. 59, No. 3, 1999, pp. 1758-1775. doi:10.1103/PhysRevB.59.1758

