Journal of Modern Physics
Vol.3 No.7(2012), Article ID:21113,8 pages DOI:10.4236/jmp.2012.37076
Guiding of Waves between Absorbing Walls
Institute for Laser Science, University of Electro-Communications, Tokyo, Japan
Email: {dima, morinaga}@ils.uec.ac.jp
Received May 5, 2012; revised June 9, 2012; accepted June 29, 2012
Keywords: Zeno effect; atom optics; waveguides; suppression of Amplified Spontaneous Emission
ABSTRACT
Guiding of waves between parallel absorbing walls is considered. The principal mode is constructed; its absorption is estimated. The agreement with previous results about reflection of waves from absorbing walls is discussed. Roughly, the effective absorption of the principal mode is proportional the minus third power of the distance between walls, minus 1.5d power of the wavenumber and minus 0.5d power of the local absorption of the wave in the wall. This estimate is suggested as hint for the design of the atomic waveguides, and also as tool for optimization of attenuation of the amplified spontaneous emission (and suppression of parasitic oscillations) in high power lasers.
1. Introduction
The consideration of reflection of waves from absorbing walls had been stimulated by the experiments with ridged mirrors [1] and their interpretation in terms of the Zeno effect [2,3]. The Zeno approximation [2] showed good agreement with experiments in wide range of parameters [3,4]; it describes reflection of waves of any origin. In particular, it applies to the atomic waves and to the optical waves.
In addition to the atom optics (discussed in [2]), the reflection and guiding of waves may affect the suppression of the Amplified Spontaneous Emission (ASE) that is considered as serious problem [5-9]. At the scaling-up the power, the efficient suppression of ASE becomes more important, and the unwanted guiding of ASE by the absorber (which is supposed to suppress it) might take place. The estimates of the conditions of such a guiding is necessary tool for the design of powerful devices.
In this article, the wave function of a particle (atom, photon) between two absorbing walls is constructed. The effective absorption of such a mode is estimated and compared to the previous results. The results are expected to have applications in both the atom optics (wanted guiding of neutral particles by the absorbing walls) and the design of powerful lasers (estimates of conditions of the unwanted guiding of the ASE by the walls that are supposer to absorb the ASE, and optimization of suppression of the ASE).
This article is organized in the following way:
In section 2, the phenomenological absorbing Schrö- denger equation is suggested. The case with absorbing walls corresponds to the pure anti Hermitian potential. The frequency of decay is denotes with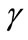 . The special system of units is used in such a way that
. The special system of units is used in such a way that  and the energy of the particle in vacuum is assumed to be square of its wavenumber.
and the energy of the particle in vacuum is assumed to be square of its wavenumber.
In section 3, the special case of uniform absorption is considered; this gives relations between parameters of the wave function and the physical quantities that can be determined experimentally. Such physical quantities are energy 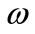 of the particle and its absorpfion
of the particle and its absorpfion 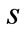 in the material of the wall; this quantities are assumed to be independent parameters.
in the material of the wall; this quantities are assumed to be independent parameters.
In section 4, the case of channeling is considered; parameters of the principal mode (transversal wavenumber , decay
, decay 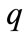 and the damping
and the damping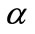 ) are defined and expressed through the holomorphic function
) are defined and expressed through the holomorphic function  , its inverse function
, its inverse function 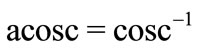 and
and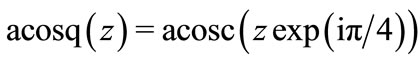 ; properties of these functions are discussed and the efficient C++ implementations are indicated.
; properties of these functions are discussed and the efficient C++ implementations are indicated.
In section 5, the example of the principal mode is considered; the real and imaginary parts of the wave functions are built through the trigonometric function of complex argument and complex exponential for the damping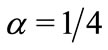 . The amplitude and phase of the principal mode are shown for
. The amplitude and phase of the principal mode are shown for 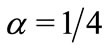 and for
and for 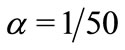 .
.
In section 6, the asymptotic behavior of parameters at small damping is considered; this is realistic case of good guiding conditions.
In section 7, the estimates for the effective absorption of the principal mode are compared with the previous results; the agreement is interpreted as confirmation of the validity of the analysis.
In section 8, the special case is suggested for physically realistic parameters of the experimental conditions of realization of the guiding of waves between absorbing walls.
In section 9 (Conclusion), the asymptotic estimate of the effective absorption  of the guided mode through the real and imaginary parts
of the guided mode through the real and imaginary parts ,
,  of the wavenumber in the wall is suggested. This main result is expected to be confirmed (or rejected) by the physical experiments with photons, atoms or any other wave of any origin.
of the wavenumber in the wall is suggested. This main result is expected to be confirmed (or rejected) by the physical experiments with photons, atoms or any other wave of any origin.
2. Schrödinger Wave and the Absorption
In this case the dimension less Schrödinger equation is considered in the paraxial approximation.
For simplicity, in this section the special system of units is used such that  and mass of the atom is half. Then, the Schrödinger equation for the wave function
and mass of the atom is half. Then, the Schrödinger equation for the wave function 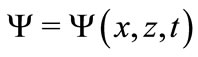 can be written as follows
can be written as follows
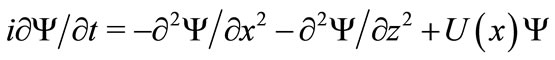 (1)
(1)
where the potential 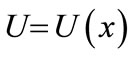 depends only on the transversal coordinate
depends only on the transversal coordinate 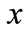 (and does not depend on time
(and does not depend on time  in the direction of propagation).
in the direction of propagation).
In the simplest approximation, the entangling with numerous degrees of freedom of scattered (or relaxed) atom can be taken into account with non Hermitian potential. Such an approximation is considered, in particular, in the interpretation of the quantum reflection in therms of the Zeno effect [2]. For the wave guide, the absorption correspond to complex values of 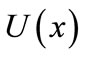 at
at , where
, where  is half-width of the channel between the mirrors.
is half-width of the channel between the mirrors.
Consider the quasi-monochromatic solution, assuming the exponential dependence on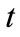 ; let
; let
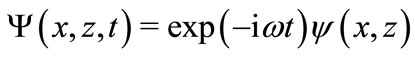 (2)
(2)
Then, instead of (1) we get the stationary Schrödinger equation
 (3)
(3)
below, the two cases of the solution are considered: for
 (4)
(4)
and for
 (5)
(5)
where 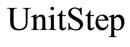 is the conventional unit step function implemented in various programming languages including Mathematica, and
is the conventional unit step function implemented in various programming languages including Mathematica, and 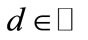 is constant, that has sense of half-width of the channel that confines the particle.
is constant, that has sense of half-width of the channel that confines the particle.
3. Uniform Absorption
In order to understand the physical sense to the constant , consider the case of the uniform absorption of the plane wave at
, consider the case of the uniform absorption of the plane wave at  by (4); let
by (4); let  does not depend on the first argument, id est,
does not depend on the first argument, id est,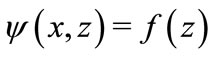 . Then, for
. Then, for  we get the equation
we get the equation
 (6)
(6)
At positive values of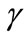 , the decaying in the direction
, the decaying in the direction 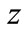 solution has form
solution has form
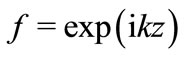 (7)
(7)
where  is solution of equation
is solution of equation
 (8)
(8)
Assuming ,
, 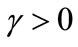 , wavenumber
, wavenumber 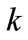 can be expressed as follows:
can be expressed as follows:
 (9)
(9)
For the compactness of notations, let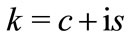 , where
, where 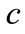 and
and  are real parameters. Then
are real parameters. Then
 (10)
(10)
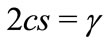 (11)
(11)
Alternatively, we may consider the absorption of wave in the medium, id est, 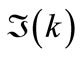 as initial parameter. Making estimates for the ridged atomic mirror with distance
as initial parameter. Making estimates for the ridged atomic mirror with distance  between ridges, the absorption by intensity can be approximated as
between ridges, the absorption by intensity can be approximated as , and the absorption by amplitude is of order of
, and the absorption by amplitude is of order of
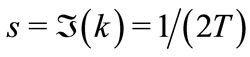 (12)
(12)
Real part of 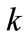 is determined by the mass and the energy of the particle we intent to reflect or to guide, or just
is determined by the mass and the energy of the particle we intent to reflect or to guide, or just , where
, where  is vacuum wavelength of the waves (perhaps, ASE) that could be guided, and
is vacuum wavelength of the waves (perhaps, ASE) that could be guided, and 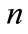 is the refraction index of the medium.
is the refraction index of the medium.
In order to avoid additional guiding by the step of the refraction index, the real part of the refraction index of the wall is supposed to be matched to that of the central region; but some reflection still may happen due to the imaginary part. Then, the real and imaginary parts of the swiare o wavenumber 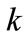 can be expressed as follows:
can be expressed as follows:
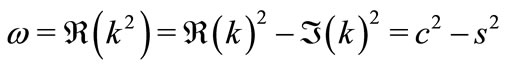 (13)
(13)
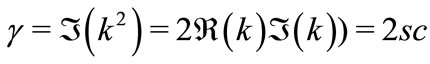 (14)
(14)
Parameter  has sense of the energy of the particle, and also sense of the square of wavenumber, while
has sense of the energy of the particle, and also sense of the square of wavenumber, while 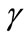 has sense of the decay rate at the time scale, if a wave would be uniform in the space. For the estimates, the term with
has sense of the decay rate at the time scale, if a wave would be uniform in the space. For the estimates, the term with 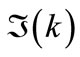 in (13) can be neglected; however it is kept in the deduction that may be applied not only to atoms, but also to other kinds of waves (optical, acoustical, waves on the surface of a liquid, etc.) For optics (both atom optics and conventional optics), the typical case is of low absorption; waves rather propagate than absorb, to,
in (13) can be neglected; however it is kept in the deduction that may be applied not only to atoms, but also to other kinds of waves (optical, acoustical, waves on the surface of a liquid, etc.) For optics (both atom optics and conventional optics), the typical case is of low absorption; waves rather propagate than absorb, to,
 (15)
(15)
In this case, for the estimate of the primary parameters, we may use the approximation
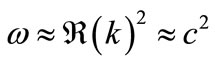 (16)
(16)
and treat 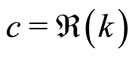 and
and  as initial parameters of the model describing the absorption of the wave inside the walls.
as initial parameters of the model describing the absorption of the wave inside the walls.
On the other hand, one may consider as “given” the energy 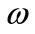 of the particle and the absorption
of the particle and the absorption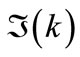 . Then,
. Then,
 (17)
(17)
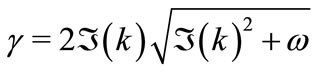 (18)
(18)
In the following consideration, parameters  and
and  and
and 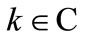 are supposed to be known. These parameters determine behavior of the wave inside the absorbing wall.
are supposed to be known. These parameters determine behavior of the wave inside the absorbing wall.
For the atom optics, id est, for the atom wave, the absorption 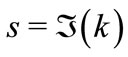 should be positive. For the optical wave, in principle, the absorption may be negative (gain medium), but the amplified spontaneous emission (unavoidable in the gain medium) limits the application of the formalism to very short distance of propagation. For this reason, the channeling in the pumped region may have more applications. In such a way, this section gives the sense to the parameters
should be positive. For the optical wave, in principle, the absorption may be negative (gain medium), but the amplified spontaneous emission (unavoidable in the gain medium) limits the application of the formalism to very short distance of propagation. For this reason, the channeling in the pumped region may have more applications. In such a way, this section gives the sense to the parameters 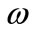 and
and 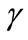 that appear in the equations (3) and (5) , that describe the channeling of a particle by the potential
that appear in the equations (3) and (5) , that describe the channeling of a particle by the potential 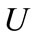 by (5). This channeling is considered in the next section. Then, the effective propagation constant
by (5). This channeling is considered in the next section. Then, the effective propagation constant  is estimated in terms of
is estimated in terms of  and half-width
and half-width  of the channel.
of the channel.
4. Channeling
For the case of potential  by (5), search the solution
by (5), search the solution 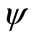 in the following form:
in the following form:
 (19)
(19)
where 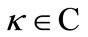 is constant.
is constant.
For the experimental realization, 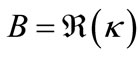 is expected to be of order of
is expected to be of order of , determined in the previous section. As for the imaginary part,
, determined in the previous section. As for the imaginary part,  is expected to be small compared to
is expected to be small compared to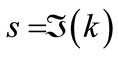 , and
, and 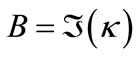 is expected to decrease as
is expected to decrease as  increases, allowing the interpretation in terms of the Zeno effect [2]: the stronger is the absorption in the region of the “observation” (id est,
increases, allowing the interpretation in terms of the Zeno effect [2]: the stronger is the absorption in the region of the “observation” (id est, ), the better is the channeling.
), the better is the channeling.
Substitution of (19) to (3) gives the equation for  in the following form:
in the following form:
 (20)
(20)
Search the solution of (20) as the combination of the cosinusoidal and the exponential, let
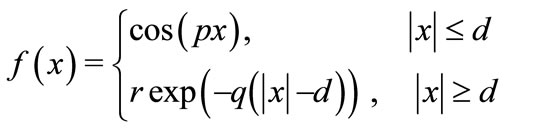 (21)
(21)
where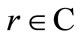 ,
,  ,
,  ,
, 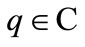 are constant parameters. From the physical reasons (almost free propagation inside the channel), parameter
are constant parameters. From the physical reasons (almost free propagation inside the channel), parameter  is expected to be of order of wavenumber
is expected to be of order of wavenumber 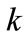 from the previous section.
from the previous section.
The substitution of (21) into (20) determines that
 (22)
(22)
 (23)
(23)
From the physical reasons, it is expected that 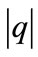 is small compared to
is small compared to  and, therefore,
and, therefore, .
.
The continuity of 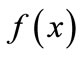 at
at 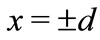 and the continuity of
and the continuity of 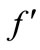 give the relations
give the relations
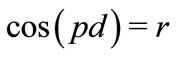 (24)
(24)
 (25)
(25)
The four equations (22), (23), (24), (25) allows to express new parameters 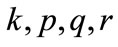 in terms of the already defined parameters
in terms of the already defined parameters  and
and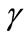 .
.
Subtraction of (23) from (22) gives
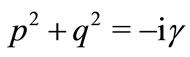 (26)
(26)
Dividing of (25) by (24) gives
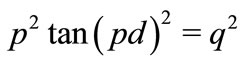 (27)
(27)
The combination of (26) and (27) gives
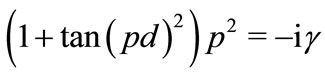 (28)
(28)
Using the relation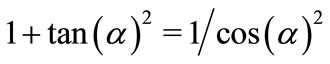 , equation (28) can be written as
, equation (28) can be written as
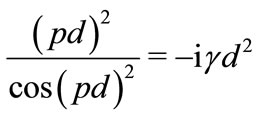 (29)
(29)
then
 (30)
(30)
This equation can be written as follows:
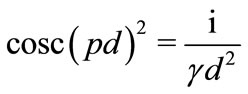 (31)
(31)
where for all complex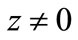 ,
,
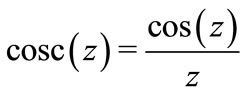 (32)
(32)
Complex map of function cosc is shown in the left hand side of figure 0; properties of this function and its inverse function 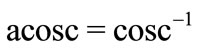 are described in TORI [10]. The name of function cosc is chosen in analogy with well established name of function sinc [11], defined with
are described in TORI [10]. The name of function cosc is chosen in analogy with well established name of function sinc [11], defined with
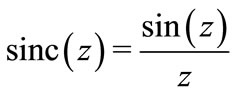 (33)
(33)
As usually, the name of the inverse function is created adding prefix “a” or “arc”.
Equation for one of solutions with 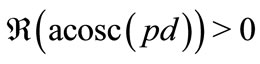 can be written as follows:
can be written as follows:
 (34)
(34)
Equation (34) can be “inverted”, giving
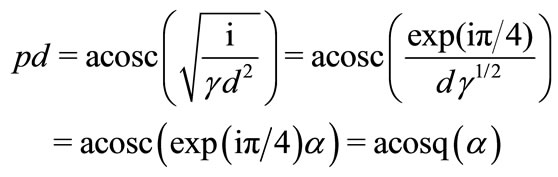 (35)
(35)
where 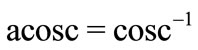 is inverse function of cosc. Damping
is inverse function of cosc. Damping  is dimensionless parameter determining the efficiency of channeling,
is dimensionless parameter determining the efficiency of channeling,
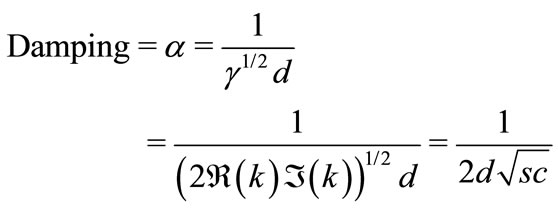 (36)
(36)
Properties of function acosc are described at TORI; the efficient implementation in C++ is suggested [10]. The complex map of acosc is show in the right hand side of figure 1 with levels of constant real part and levels of constant imaginary part. Behavior of real and imaginary parts of function acosq of real argument is shown in fthe left hand side of figure 2.
The decay rate of mode in the region with absorption is determined with parameter . Once
. Once  is determined, from equation (27),
is determined, from equation (27),
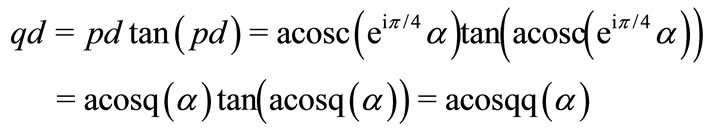 (37)
(37)
Function acosqq is shown in the right hand part of figure 2.

Figure 1. Complex map of function  by (32) , left, and that of
by (32) , left, and that of  by [10], right, in the
by [10], right, in the ,
,  plane. Levels
plane. Levels 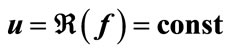 and levels
and levels 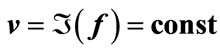 are shown.
are shown.
Figure 2.  and
and  by (35), left;
by (35), left;  and
and  by (35), right.
by (35), right.
5. Assembling of Mode, Example
The damping  by (36) determines the properties of the mode with given distance
by (36) determines the properties of the mode with given distance  between walls and given real and imaginary parts of the wavenumber
between walls and given real and imaginary parts of the wavenumber  that determines the propagation of wave in the material of the wall. With tools defined above, the principal mode of wave guided between absorbing walls is expressed with equation (21). Parameters
that determines the propagation of wave in the material of the wall. With tools defined above, the principal mode of wave guided between absorbing walls is expressed with equation (21). Parameters ,
, 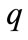 and
and 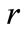 are defined with equations (35), (37), (24).
are defined with equations (35), (37), (24).
As an example of the assembling of such a mode, the case  is presented in figure 3; the real and imaginary parts of the components of function
is presented in figure 3; the real and imaginary parts of the components of function  are plotted versus dimensionless product
are plotted versus dimensionless product . In this case,
. In this case,
 (38)
(38)
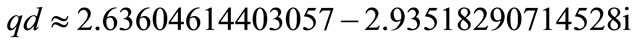 (39)
(39)
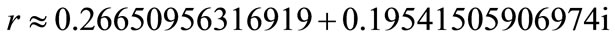 (40)
(40)
The amplitude and phase of the mode 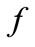 for
for  and
and 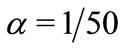 are shown in figure 4. for
are shown in figure 4. for , the parameters are
, the parameters are
 (41)
(41)
 (42)
(42)
 (43)
(43)
With functions ArcCosq and ArcCosqq implemented in TORI through [10], one can easy assemble the principal mode for other values of the damping parameter  with minimal modification of the codes supplied there.
with minimal modification of the codes supplied there.
6. Application to Atomic Waves and the Asymptotic
The effective absorption of a guided mode is one of most important parameters of any waveguide. This section consider the case of low damping and, correspondently, strong channeling.
According to (19) the effective absorption is determined by parameter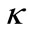 ,
,
 (44)
(44)
From equation (22),
 (45)
(45)
The real and imaginary parts of 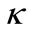 determine the effective wavenumber and absorption of the guided mode “exactly” in the mathematical sense. As for the physical applications, the case of strong guiding (and low absorption) is of interest. This case corresponds to the small values of the damping parameter
determine the effective wavenumber and absorption of the guided mode “exactly” in the mathematical sense. As for the physical applications, the case of strong guiding (and low absorption) is of interest. This case corresponds to the small values of the damping parameter , and the asymptotic behavior of the absorption of the guided mode is considered in this section.
, and the asymptotic behavior of the absorption of the guided mode is considered in this section.
For the strong guiding, the propagation constant  can be expanded as follows:
can be expanded as follows:
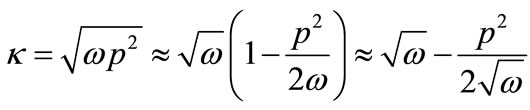 (46)
(46)
then, the absorption 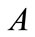 of the mode can be expressed as follows:
of the mode can be expressed as follows:
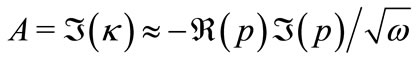 (47)
(47)
In order to provide the flux of probability from the center of mode to the absorbing walls, the imaginary part of the transversal wavenumber should be negative,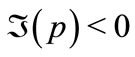 . The expansion of funciton acocq at zero gives:
. The expansion of funciton acocq at zero gives:
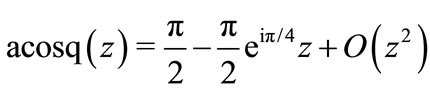 (48)
(48)
This gives the approximation for the transversal wavenumber 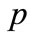 in the following form:
in the following form:
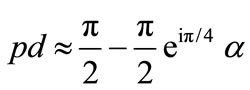 (49)
(49)
and the estimate for the effective absorption
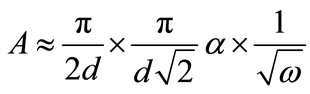 (50)
(50)
Then, 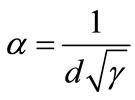 by (36) and
by (36) and 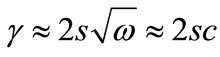 should be used, giving
should be used, giving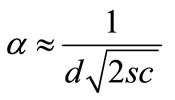 . Then, the effective absorption of the mode
. Then, the effective absorption of the mode
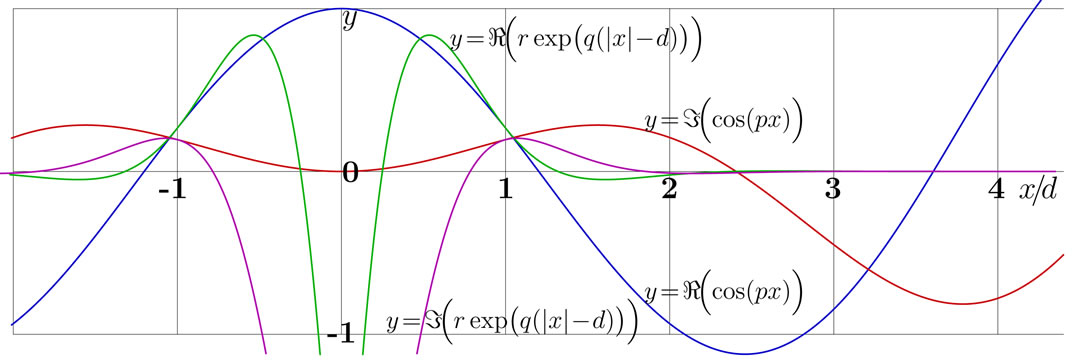
Figure 3. Combination of mode (21) from the cosinusoidal and the exponents for α = 1/4.

Figure 4. Amplitude and phase of the mode f by (21) for α = 1/4 and for α = 1/50.
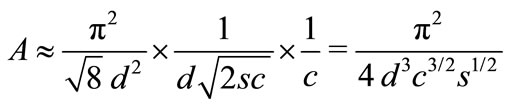 (51)
(51)
where 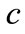 has sense of wavenumber, and
has sense of wavenumber, and 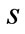 is the absorption in the wall.
is the absorption in the wall.
In the similar way, the highest modes can be constructed. For the mth transversal mode, the transversal wavenumber scales proportionally to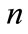 ; and the absorption of mode scales proportionally to
; and the absorption of mode scales proportionally to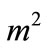 .
.
7. Comparison to Previous Results
The absorption of mode can be interpreted also in terms of the multiple reflection of guided wave from the walls. The coefficient of reflection  is estimated in the description of the ridged mirrors in terms of the Zeno effect [2],
is estimated in the description of the ridged mirrors in terms of the Zeno effect [2],
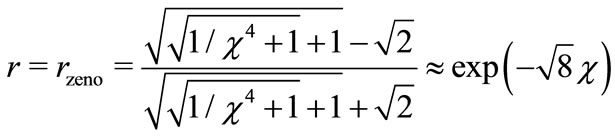 (52)
(52)
where
 (53)
(53)
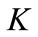 is wavenumber and can be replaced to
is wavenumber and can be replaced to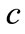 ; while
; while 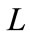 is distance between idealized absorbers that can be approximated as
is distance between idealized absorbers that can be approximated as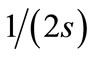 , and
, and  is the grazing angle. (Notation
is the grazing angle. (Notation 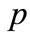 of [2] is not used here, to keep letter
of [2] is not used here, to keep letter 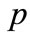 denoting the transversal wavenumber; so, in (52) and (53) , notation
denoting the transversal wavenumber; so, in (52) and (53) , notation  is used instead.)
is used instead.)
For the good channeling conditions, the effective absorption can be approximated with
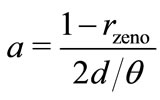 (54)
(54)
where 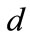 is half-width of the channel and
is half-width of the channel and  is ratio of the transversal wavenumber
is ratio of the transversal wavenumber
 (55)
(55)
to the wavenumber . At the reflection of wave from a ridged mirror,
. At the reflection of wave from a ridged mirror,  plays role of the grazing angle.
plays role of the grazing angle.
Substitution of (52) and (55) into (54) gives the following expression for the absorption
 (56)
(56)
The grazing angle can be approximated with
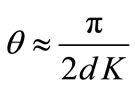 (57)
(57)
giving the estimate for the efficient absorption
 (58)
(58)
For the comparison to the previous result, 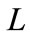 should be replaced to
should be replaced to 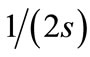 and
and  should be replaced to
should be replaced to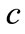 , giving the absorption by probability
, giving the absorption by probability
 (59)
(59)
This expression should be compared to (51).
In the first approximation, the consideration of the multiple reflection from absorbing walls and the consideration of mode guided between the absorbing walls give the same prediction about effective absorption of this mode. The consideration of the multiple reflection from absorbing walls and the consideration of mode guided between the absorbing walls give the same prediction about effective absorption of this mode.
8. Numerical Example
Consider the application of the estimate (59) for the guiding of the realistic laser beam. Assume, the absorption in the walls
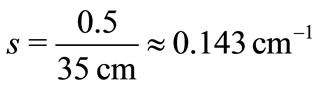 (60)
(60)
Following the ideology of the Zeno interpretation of absorbing walls [2], such an absorption may be approximated with series of slits separated by distance 35 mm.
Let the wavenumber is
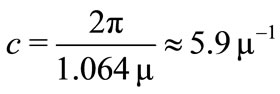 (61)
(61)
Let the halfwidth of the channel
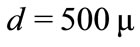 (62)
(62)
This gives the estimate for the absorption of guided modes,
 (63)
(63)
For the principal mode ( ), after to propagate distance
), after to propagate distance , the attenuation factor is of order of
, the attenuation factor is of order of
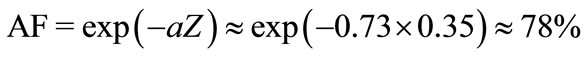 (64)
(64)
that means, that the most of the initial power of the guided mode is still delivered. As for the second mode, its attenuation
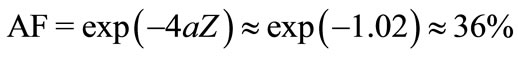 (65)
(65)
that means significant dicrimination of the second mode.
Using the approximation of the set of absorbers as a continuous medium [2], the example above may correspond to transfer of near infra-red light through the set of 10 slits separated with distance 35 mm. Roughly, the amplitude of field after the set of slits can be approximates with the cosinusoidal profile. However, the presence of the highest modes, as well as the diffraction of the tails of the mode on the edges should make the similarity qualitative. Similar result one may expect to observe at propagation of light through the set of pinholes of radius . The similarity with the idealized cosinusoidal or Besseliean mode should improve at the increase of number of slits or pinholes; a hundred of silts or pinholes may be sufficient to get the quantitative agreement with the idealized cosinusoidal or Besselian profile.
. The similarity with the idealized cosinusoidal or Besseliean mode should improve at the increase of number of slits or pinholes; a hundred of silts or pinholes may be sufficient to get the quantitative agreement with the idealized cosinusoidal or Besselian profile.
The accurate consideration of the discrete character of the absorbing walls, as well as construction of the mode for the case with circular symmetry may be continuation of this work. For the paraxial case, the estimates are universal and are not sensitive to the origin of waves. In particular, the results are expected to apply to the electromagnetic waves as well as to the cold atoms, exhibiting the wave properties.
9. Conclusions
Guiding of wave of any origin between absorbing walls is considered. Wavenumber  and the amplitude absorption
and the amplitude absorption  of wave in the wall, and the half-width
of wave in the wall, and the half-width 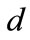 of the channel are considered as given parameters.
of the channel are considered as given parameters.
The dimensionless damping parameter 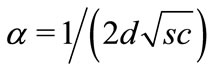 by (36) is suggested to characterize the scale of the effect.
by (36) is suggested to characterize the scale of the effect.
The first (principal) mode (21) with lowest absorption is explicitly constructed. The transversal wavenumber  of the mode is expressed through the function acosc of complex argument; properties of this function are described and the numerical implementation is supplied [10]. The propagation constant
of the mode is expressed through the function acosc of complex argument; properties of this function are described and the numerical implementation is supplied [10]. The propagation constant 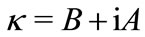 is expressed with equation (45); the asymptotic estimate (51) of the absorption
is expressed with equation (45); the asymptotic estimate (51) of the absorption  of the mode is suggested. The estimate agrees with that on the base of the Zeno reflection of the waves from the absorbing medium reported earlier [2].
of the mode is suggested. The estimate agrees with that on the base of the Zeno reflection of the waves from the absorbing medium reported earlier [2].
The estimates above are important in the design of the suppression of the amplified spontaneous emission (ASE) in the high power lasers. The guiding of modes by the absorption walls happens whenever the engineers want this effect or not. Similar estimate is valid for the highest modes. For the mth transversal mode, the asymptotic estimate is suggested for the absorption
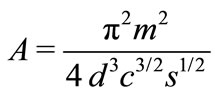 (66)
(66)
through the half-width 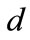 of the channel, wavenumber
of the channel, wavenumber  and absorption
and absorption 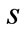 of wave in the walls.
of wave in the walls.
Similar estimate (with slightly higher absorption) correspond to the case with circular symmetry, that can be treated in the similar way; the mode is expressed with the Bessel function, parameter  plays role of the radius of the channel. At small value of damping
plays role of the radius of the channel. At small value of damping 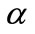 by (36), the transversal wavenumber
by (36), the transversal wavenumber 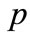 is almost real.
is almost real.
The result should be useful in both, wanted guiding of cold neutral particles by their detection (absorption) and the efficient suppression of the unwanted guiding of waves, for example, ASE in powerful optical amplifiers, and optimization of the ASE absorbers.
10. Acknowledgements
Authors are grateful to Dr. Hilmar Oberst and Prof. Fujio Shimizu and Prof. Kazuko Shimizu for the collaboration.
REFERENCES
- F. Shimizu and J. Fujita, “Giant Quantum Reflection of Neon Atoms from a Ridged Silicon Surface,” Journal of the Physical Society of Japan, Vol. 71, No. 1, 2002, pp. 5-8. doi:10.1143/JPSJ.71.5
- D. Kouznetsov and H. Obrest, “Reflection of Waves from a Ridged Surface and the Zeno Effect,” Optical Review, Vol. 12, No. 5, 2005, pp. 363-366. doi:10.1007/s10043-005-0363-9
- D. Kouznetsov and H. Oberst, “Scattering of Waves at Ridged Mirrors,” Physical Review A, Vol. 72, No. 1, 2005, p. 013617. doi:10.1103/PhysRevA.72.013617
- D. Kouznetsov, H. Oberst, K. Shimizu, A. Neumann, Y. Kuznetsova, J.-F. Bisson, K. Ueda and S. R. J. Brueck, “Ridged Atomic Mirrors and Atomic Nanoscope,” Journal of Physics B, Vol. 39, No. 7, 2006, pp. 1605-1616. doi:10.1088/0953-4075/39/7/005
- J. Itatani, J. Faure, M. Nantel, G. Mourou and S. Watanabe, “Suppression of the Amplified Spontaneous Emission in Chirped-Pulse-Amplification Lasers by Clean HighEnergy Seed-Pulse Injection,” Optics Communications, Vol. 148, No. 1-3, 1998, pp. 70-74.
- H. Yagi, J. F. Bisson, K. Ueda and T. Yanagitani, “Y3Al5O12 Ceramic Absorbers for the Suppression of Parasitic Oscillation in High-Power Nd:YAG Lasers,” Journal of Luminescence, Vol. 121, No. 1, 2006, pp. 88-94. http://www.sciencedirect.com/science/article/pii/S0022231305002504
- K. Ertel, C. Hooker, S. J. Hawkes, B. T. Parry and J. L. Collier, “ASE Suppression in a High Energy Titanium Sapphire Amplifier,” Optics Express, Vol. 16, No. 11, 2008, pp. 8039-8049. doi:10.1364/OE.16.008039
- L. A. Hackel, T. F. Soules, S. N. Fochs, M. D. Rotter and S. A. Letts, “A Method for Suppressing ASE and Parasitic Oscillations in a High Average Power Solid-State Laser,” Patent US7463660, 2008. http://www.google.com/patents/US20050254536
- A. K. Sridharan, S. Saraf, S. Sinha and R. L. Byer, “Zigzag Slabs for Solid-State Laser Amplifiers: Batch Fabrication and Parasitic Oscillation Suppression,” Applied Optics, Vol. 45, No. 14, 2006, pp. 3340-3351. doi:10.1364/AO.45.003340
- http://tori.ils.uec.ac.jp/TORI/index.php/ArcCosc
- http://mathworld.wolfram.com/SincFunction.html

