Journal of Modern Physics
Vol.3 No.3(2012), Article ID:18200,6 pages DOI:10.4236/jmp.2012.33035
New Approach to Simulating the Absorption of Gamma Radiations Using the Monte-Carlo Method: A Computational Study
Institute for Advanced Studies, Tehran, Iran
Email: *mohammadalighorbani1983@yahoo.com
Received October 31, 2011; revised December 13, 2011; accepted December 27, 2011
Keywords: Simulation; Photon Transport; Material; Monte-Carlo Method; Klein-Nishina Distribution
ABSTRACT
Simulating the absorption of gamma radiations through the Monte-Carlo is a method that has been widely employed to compute the absorption of these radiations in various materials and shapes. In such simulations, the method of sampling the photons’ scattering angle from the Klein-Nishina distribution is of particular significance. In this paper, to apply the Klein-Nishina distribution to the photons’ scattering, a method of weighing is proposed that possesses higher accuracy and velocity in comparison to other existing methods, and it is applicable to all the photons with energy higher than 1 keV. Through this method, a fraction of photons’ energy absorbed into the different-sized spheres made of water is calculated and compared with the results achieved using other methods. Since the results are excellently consistent with the weighing method’s results, it can be substituted for the other methods.
1. Introduction
The simulation of photon transport in material through the Monte-Carlo method is a method that is applied to the computations of the design of the essential shielding against X-ray and gamma-ray sources, the design of the detectors with appropriate size and material for detecting this type of radiations, and the nuclear medicine to determine the dose absorbed into the body’s different tissues due to consuming radioactive materials. In such calculations, to determine the radiant energy absorbed into the material containing radioactive source or the material sitting in front of the source, a photon with specified energy is produced in a random trajectory, and its story is defined during the following steps [1]:
1) The distance x the photon traverses to interact is randomly chosen (sampling) using the below equation:
 (1)
(1)
where p is the random number (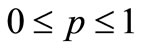 ), and µ is the linear attenuation coefficient of γ radiation (with the energy
), and µ is the linear attenuation coefficient of γ radiation (with the energy ) in the material.
) in the material.
2) If the location of interaction is outside the absorptive material, the story of photon will end, the energy absorbed into the material is considered zero, and the program starts from the beginning for another event.
3) If the location of interaction is inside the absorptive material, the type of interaction (photoelectric, Compton scattering, and pair production) is determined using random numbers and considering the values of respective cross sections.
4) If the type of interaction is photoelectric, the story of photon will end, and it is assumed that the total energy of photon is transferred to the absorptive body. Providing that the pair production occurs, 1.02 MeV of the incident photon energy, which is related to the next pair-annihilation process, is traced in material; it is assumed that the remnant of incident photon energy is absorbed into material.
5) If the type of interaction is Compton scattering, the respective differential cross section given by the KleinNishina equation is sampled; through using it, the new scattered photon trajectory is determined (the Klein-Nishina equation is introduced in the next section). Herein, the energy absorbed into this point of interaction is calculated, and then, the steps A to E are repeated for the scattered photons.
Therefore, photons are traced in material; with regards to the absorptive material’s dimensions, the below fraction is computed for each event:
 (2)
(2)
This process is repeated for a substantial number of photons, and the average value of absorbed fraction 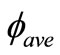 is computed.
is computed.
In the above steps, sampling the Klein-Nishina distribution is a sensitive section. It means that in each photon scattering by electron, the photon scattering angle (θ) should be selected so that the photons’ angular distribution for a large number of events conforms to the KleinNishina equation. Various methods of sampling the angle θ from the Klein-Nishina probability distribution are proposed that are mainly based inversion methods [2], approximate inversion methods [3-5], uniform rejection methods [6,7], and non-uniform rejection methods [8-13]. In the inversion methods, since the inverse solution to the collective density function, which is obtained through integrating the Klein-Nishina equation, is not analytically possible, the numerical methods such as the Newton’s method should be employed to solve it. This method is lengthy and time-consuming. Also, Koblinger [14] indicated that provided the energy of incident gamma ray is higher than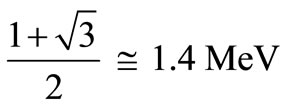 , the KleinNishina distribution function can be written as the sum of four positive functions whose collective density functions’ inverse solution is analytically possible. Therefore, if the gamma-ray energy is higher than 1.4 MeV, the scattering angle of photons can be directly sampled using this method. A comprehensive study of various methods conducted by Blomquist and Gelbard [15] indicates that the Kahn’s method [11-13] (a non-uniform rejection method) and Koblinger’s method [14] are respectively the most appropriate sampling methods at low energies and energies higher than 1.4 MeV (
, the KleinNishina distribution function can be written as the sum of four positive functions whose collective density functions’ inverse solution is analytically possible. Therefore, if the gamma-ray energy is higher than 1.4 MeV, the scattering angle of photons can be directly sampled using this method. A comprehensive study of various methods conducted by Blomquist and Gelbard [15] indicates that the Kahn’s method [11-13] (a non-uniform rejection method) and Koblinger’s method [14] are respectively the most appropriate sampling methods at low energies and energies higher than 1.4 MeV ( ). Le et al. [16] employed an approximate inversion method in the calculations of detections with limited dimensions. However, the approximate inversion methods are not applied in cases where high accuracy is required since these methods are not fairly accurate.
). Le et al. [16] employed an approximate inversion method in the calculations of detections with limited dimensions. However, the approximate inversion methods are not applied in cases where high accuracy is required since these methods are not fairly accurate.
In this paper, a novel method to consider the KleinNishina distribution for the scattering angle θ is proposed; how we compute  (absorbed fraction) using this method is described. Since a weight is calculated for each event, this method is termed the weighing method. This method is completely different from the weight methods used to compute integrals through Monte-Carlo and other weight methods provided in the reference [2].
(absorbed fraction) using this method is described. Since a weight is calculated for each event, this method is termed the weighing method. This method is completely different from the weight methods used to compute integrals through Monte-Carlo and other weight methods provided in the reference [2].
2. The Essential Equations and Weighing Method
2.1. The Essential Equations
In this section, we introduce the equations related to the photons’ scattering applied to the weighing method. When a photon with the energy 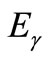 collides with an electron and scatters, the angular distribution of scattered photons conforms with the below equation (Klein-Nishina):
collides with an electron and scatters, the angular distribution of scattered photons conforms with the below equation (Klein-Nishina):
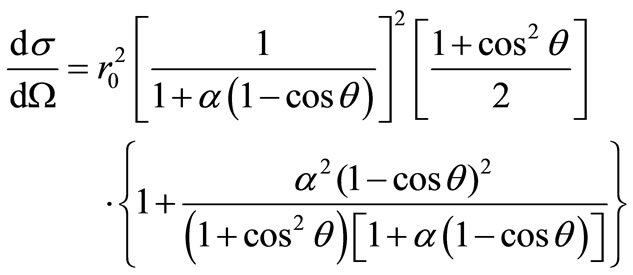 (3)
(3)
where θ is the angle between the scattered photons and incident photon direction, 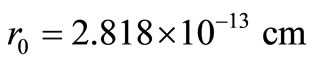 (classical electron radius), and α is the proportion of incident photon energy to electron rest energy (
(classical electron radius), and α is the proportion of incident photon energy to electron rest energy (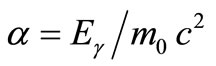 ). Through integrating the above equation over the whole space of cross section, Compton scattering (
). Through integrating the above equation over the whole space of cross section, Compton scattering (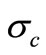 ) is achieved for an electron as the form below:
) is achieved for an electron as the form below:
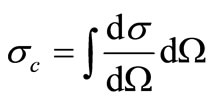 (4)
(4)
 (5)
(5)
In Compton scattering, the energy of scattered photon (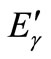 ) relates to the energy of radiant photon (
) relates to the energy of radiant photon (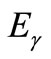 ) as the following equation:
) as the following equation:
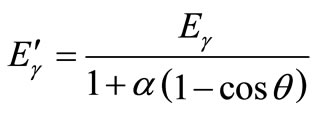 (6)
(6)
Therefore, in a Compton collision, in which the photon is scattered under the angle of θ, the energy received by the target electron is as follows:
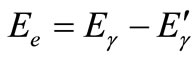 (7)
(7)
The energy distribution of target electrons is given by the equation below:
 (8)
(8)
and the energy of target electron according to the scattering angle is as the following form:
 (9)
(9)
The maximum energy the target electron can carry in a collision is as follows:
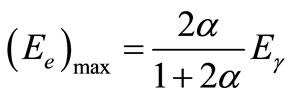 (10)
(10)
2.2. The Weighing Method
To study the Klein-Nishina non-uniform distribution function (Equation (3)) in the scattering of photons, a random number generator (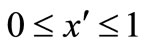 ) can be utilized,
) can be utilized, 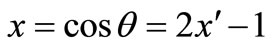 , a weight proportional to the value of Klein-Nishina function at the point x can be attributed to each event, and the next computations can be performed with regards to these weights. Therefore, since the attributed weight is proportional to the value of Klein-Nishina function, this non-uniform function is easily considered. The period of computation is shorter because there is not any rejected event. Consequently, in a shorter period of time, an acceptable statistical accuracy can be achieved through creating a substantial number of events.
, a weight proportional to the value of Klein-Nishina function at the point x can be attributed to each event, and the next computations can be performed with regards to these weights. Therefore, since the attributed weight is proportional to the value of Klein-Nishina function, this non-uniform function is easily considered. The period of computation is shorter because there is not any rejected event. Consequently, in a shorter period of time, an acceptable statistical accuracy can be achieved through creating a substantial number of events.
Each event’s weight can be obtained by the simple method below. In a uniform distribution of variable x changing within the range of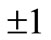 , the probability of x being between x and
, the probability of x being between x and  equals
equals . On the other hand, based on the Klein-Nishina distribution, the probability of x being between x and
. On the other hand, based on the Klein-Nishina distribution, the probability of x being between x and 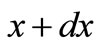 is as follows:
is as follows:
 (11)
(11)
To transform the uniform distribution into Klein-Nishina distribution,  can be multiplied by the weight W (as a function of x):
can be multiplied by the weight W (as a function of x):
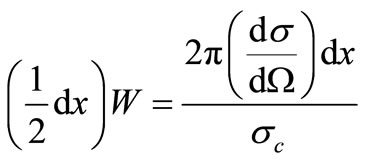 (12)
(12)
consequently,
 (13)
(13)
If the angle θ is substituted for x, and produced within the range of 0 to π, the respective weight should be as the following form:
 (14)
(14)
where . Equation (8) may be employedand x is considered as the energy of scattered electron that can change from zero to
. Equation (8) may be employedand x is considered as the energy of scattered electron that can change from zero to  (Equation (10)). The below weight can be attributed to each selected x:
(Equation (10)). The below weight can be attributed to each selected x:
 (15)
(15)
3. Results and Discussion
3.1. The Speed and Accuracy of Weighing Method
The angular distribution of scattered photons at several energies (50,000 events for each energy) is produced through various methods (weighing, Kahn [12,13], and Koblinger [14]); the mean relative deviation (MRD) of distribution achieved by the theoretical distribution (KleinNishina) is computed for each case. These computations’ results provided in Table 1 indicate that the weighing method, which is applicable throughout the gamma-ray energy range, is more accurate (for the same number of events) than the other methods. The above-mentioned mean relative deviation is defined as follows:
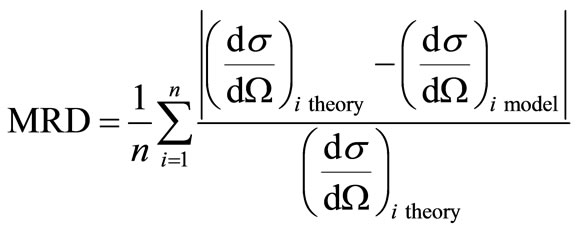 (16)
(16)
where n is the number of classes ( for the performed computations).
for the performed computations).
In sampling from the Klein-Nishina distribution through various methods, the period of running program for each case is recorded to observe and compare the speed of different methods. These observations’ results are illustrated in Figure 1. As can be seen, for , the Kahn’s method is quicker than the Koblinger’s method; for
, the Kahn’s method is quicker than the Koblinger’s method; for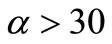 , considering that the efficiency of Kahn’s method dramatically declines, the Koblinger’s method can be considered quicker. These results are totally consistent with the results obtained by Blomquist and Gelbard [15]. This figure also indicates that, throughout the energy range, the weighing method is quicker than both methods of Kahn and Koblinger. For
, considering that the efficiency of Kahn’s method dramatically declines, the Koblinger’s method can be considered quicker. These results are totally consistent with the results obtained by Blomquist and Gelbard [15]. This figure also indicates that, throughout the energy range, the weighing method is quicker than both methods of Kahn and Koblinger. For , this method is far quicker than the Kahn’s method, and approximately two times quicker than the Koblinger’s method.
, this method is far quicker than the Kahn’s method, and approximately two times quicker than the Koblinger’s method.
3.2. The Computation of the Absorbed Fraction of Energy
The absorbed fraction of energy (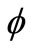 ) is calculated during the steps mentioned in the introduction. However, to compute it using the weighing method, the photons’ scattering angle based on a planar distribution (
) is calculated during the steps mentioned in the introduction. However, to compute it using the weighing method, the photons’ scattering angle based on a planar distribution ( ) is selected instead of sampling the Klein-Nishina distribution, a weight is attributed to each event, and the weighted average of absorbed fraction of energy for N events is calculated using the following equation:
) is selected instead of sampling the Klein-Nishina distribution, a weight is attributed to each event, and the weighted average of absorbed fraction of energy for N events is calculated using the following equation:
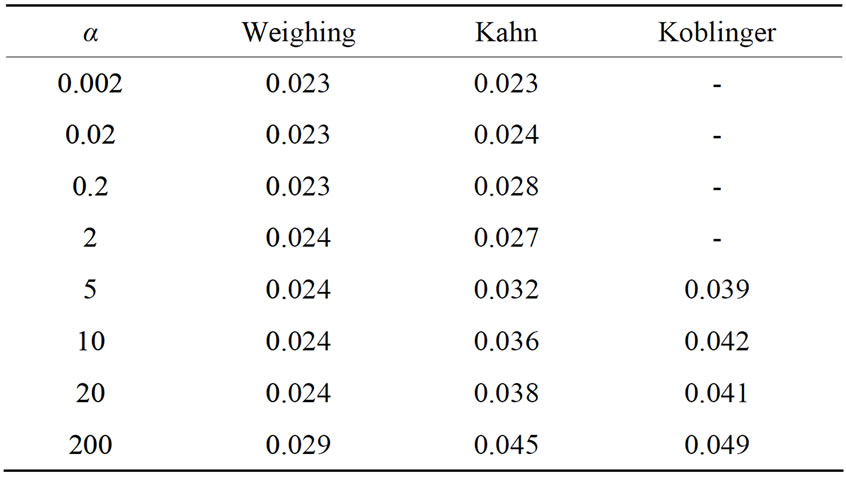
Table 1. The mean relative deviation (MRD) of different distributions from the Klein-Nishina distribution.
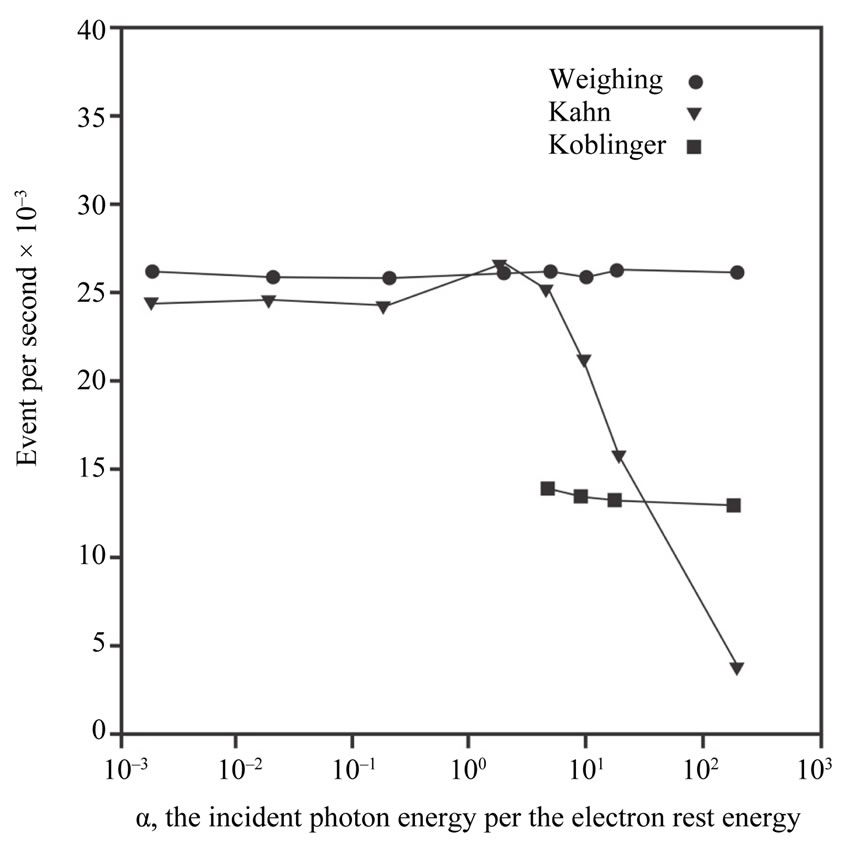
Figure 1. The different methods’ speed of sampling according to the incident photon energy.
 (17)
(17)
where 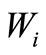 is the weight attributed to the ith event. Since each photon may have several interactions while it is moving through material, this weight is written as follows:
is the weight attributed to the ith event. Since each photon may have several interactions while it is moving through material, this weight is written as follows:
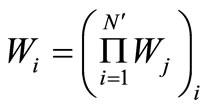 (18)
(18)
where  is the number of times the ith photon interacts while it is moving through material, and
is the number of times the ith photon interacts while it is moving through material, and 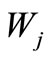 denotes the weight attributed to the jth interaction point. This weight of points where the type of interaction is Compton scattering is calculated through one of Equations (13), (14), or (15) with respect to the Klein-Nishina distribution in the respective energy, and otherwise this weight equals one.
denotes the weight attributed to the jth interaction point. This weight of points where the type of interaction is Compton scattering is calculated through one of Equations (13), (14), or (15) with respect to the Klein-Nishina distribution in the respective energy, and otherwise this weight equals one.
In the computations, we consider the gamma-ray point sources with different energies in the center of water spheres (they are very similar to the soft tissue in terms of mass density and electron density) and with different masses, and compute  through the weighing method for a large number of events (herein
through the weighing method for a large number of events (herein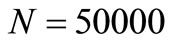 ). Some examples of these computations’ results are depicted in Figure 2. Through exploiting the cross sections used in the weighing method and the steps mentioned in the introduction,
). Some examples of these computations’ results are depicted in Figure 2. Through exploiting the cross sections used in the weighing method and the steps mentioned in the introduction, 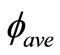 is reproduced through sampling the scattering angle of photons according to Kahn’s and Koblinger’s methods. These calculations’ results are completely consistent with the weighing method’s results. In order to compare these computations’ results with the weighing method’s results, some examples of them are illustrated in Figure 2. The Kahn’s method is compared with the weighing method at the energies either lower than 1.4 MeV (Figure 2(a)) or higher than 1.4 MeV (Figure 2(b)). The Koblinger’s method is compared with the weighing method only at the energies higher than 1.4 MeV (Figure 2(c)) since this method is solely applicable at the energies higher than this level.
is reproduced through sampling the scattering angle of photons according to Kahn’s and Koblinger’s methods. These calculations’ results are completely consistent with the weighing method’s results. In order to compare these computations’ results with the weighing method’s results, some examples of them are illustrated in Figure 2. The Kahn’s method is compared with the weighing method at the energies either lower than 1.4 MeV (Figure 2(a)) or higher than 1.4 MeV (Figure 2(b)). The Koblinger’s method is compared with the weighing method only at the energies higher than 1.4 MeV (Figure 2(c)) since this method is solely applicable at the energies higher than this level.
4. Conclusion
In this paper, for the first time, we proposed a novel analytical and numerical approach toward simulating the absorption of gamma radiations using the Monte-Carlo method. As stated in the introduction, in the simulation of photon transport in material, the photon’s scattering angle is generally sampled using the Kahn’s method at low energies, and the Koblinger’s method at energies higher than 1.4 MeV. In comparison with the methods of Kahn and Koblinger, the weighing method proposed in this paper is either more accurate (Table 1) or quicker throughout the energy range (Figure 1). In the weighing method, considering a weight that can be easily calculated for each event, the weighted average of absorbedinto-material fraction of gamma-ray energy can be computed through the mentioned method. Since the results obtained by the weighing method are completely consistent with the other recommended existing methods’ results (Figure 2), and considering the weighing method’s accuracy and speed, this method can be substituted for the other methods. In the rejection methods, since a number of events are rejected, the issue of efficiency is mooted (the ratio of the number of accepted events to the total number of produced events). At high energies, the rejection methods’ efficiency considerably decreases because increasing the gamma-ray energy changes the angular distribution of scattered photons so that a large number of events are rejected; accordingly, utilizing these methods at high energies is not recommended.
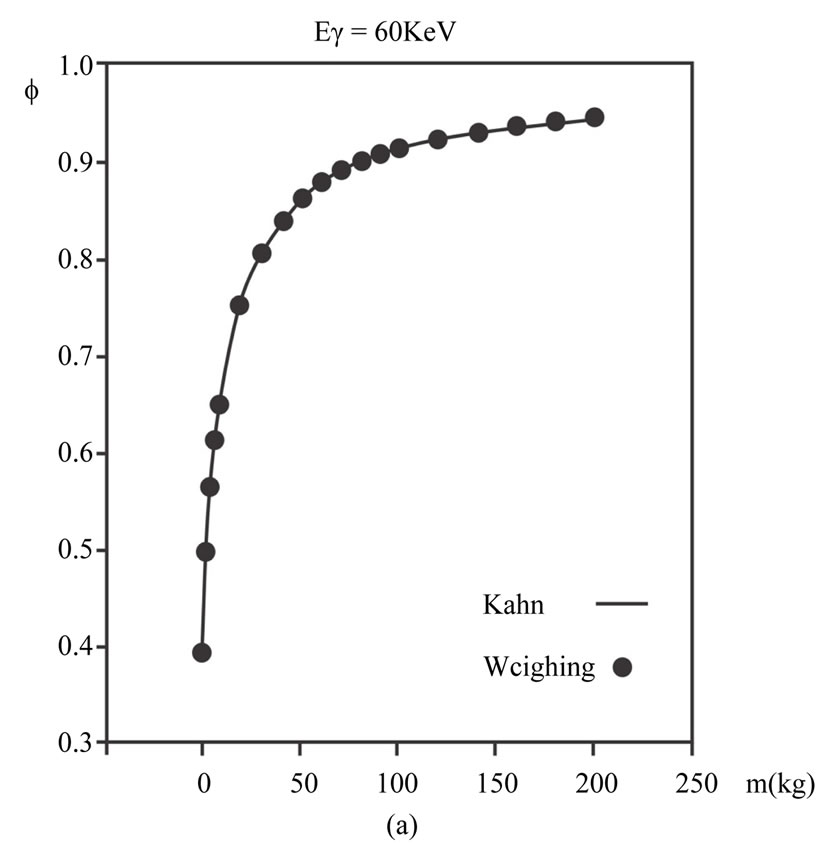
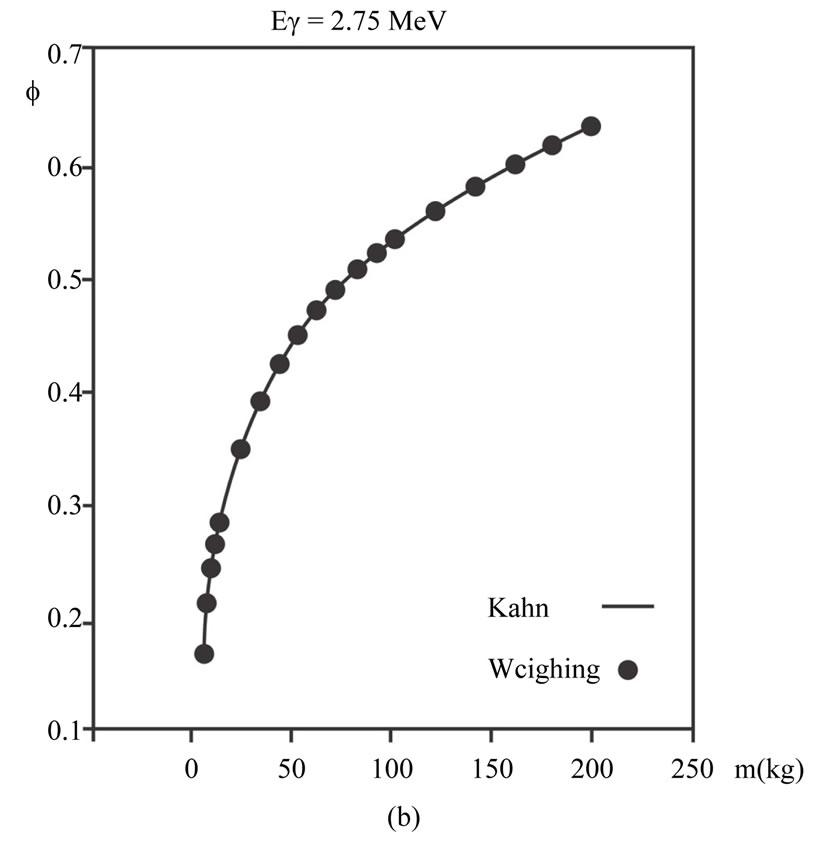
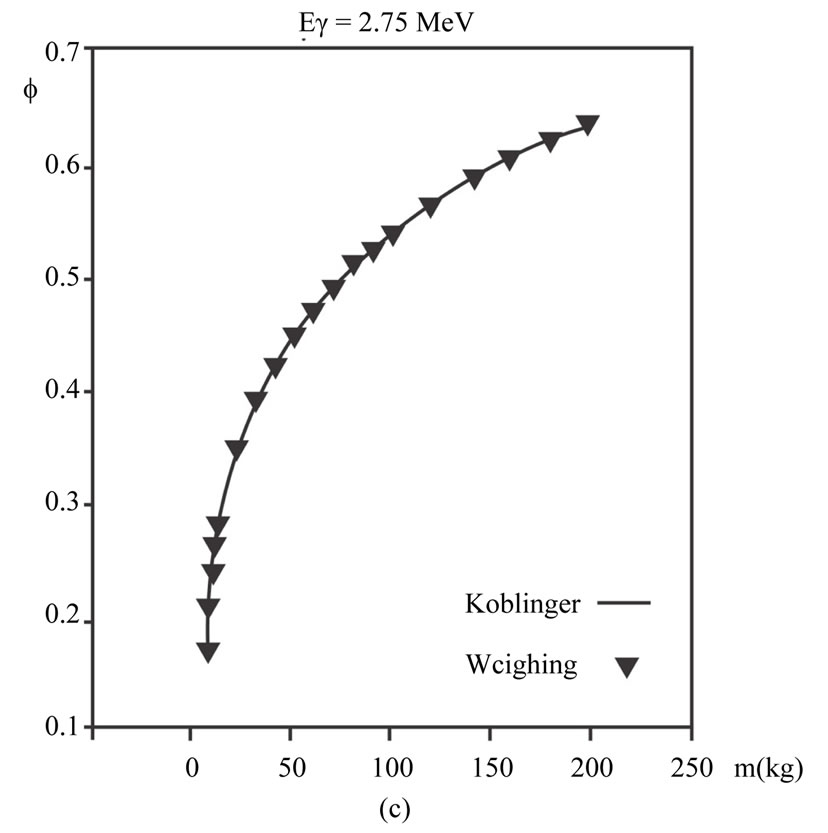
Figure 2. (a) The absorbed fraction of energy ( ) according to the water sphere’s mass, and the comparison with the methods of (b) Kahn and (c) Koblinger.
) according to the water sphere’s mass, and the comparison with the methods of (b) Kahn and (c) Koblinger.
5. Acknowledgements
The work described in this paper was fully supported by grants from the Institute for Advanced Studies of Iran. The authors would like to express genuinely and sincerely thanks and appreciated and their gratitude to Institute for Advanced Studies of Iran.
REFERENCES
- P. Andreo, “Monte Carlo Techniques in Medical Radiation Physics,” Physics in Medicine and Biology, Vol. 36, No. 7, 1991, p. 861. doi:10.1088/0031-9155/36/7/001.
- G. P. Gavanaugh and A. B. Chilton, “Angle Selection Techniques for Gamma Photons in Monte Carlo Calculations on Parellel Computers,” Nuclear Science and Engineering, Vol. 53, No. 2, 1974, pp. 256-261.
- C. J. Everett, E. D. Cashwell and G. D. Turner, “A New Method of Sampling the Klein-Nishina Probability Distribution for All Incident Photon Energies above 1 keV,” Los Alamos Scientific Laboratory, Los Alamos, 1971.
- C. J. Everett and E. D. Cashwell, “New Method of Sampling the Klein-Nishina Probability Distribution for All Incident Photon Energies above 1 keV (a Revised Complete Account). [Monte Carlo Method, Differential cross Sections],” Los Alamos Scientific Laboratory, Los Alamos, 1978. doi:10.2172/7075175.
- C. J. Everett, E. D. Cashwell and G. D. Turner, “Method of Sampling Certain Probability Densities without Inversion of Their Distribution Functions,” Los Alamos Scientific Laboratory, Los Alamos, 1973, doi:10.2172/4409123.
- A. E. Profio, D. R. Doiron and E. G. King, “Laser Fluorescence Bronchoscope for Localization of Occult Lung Tumors,” Medical Physics, Vol. 6, No. 6, 1979, pp. 523- 525.
- A. E. Profio, “Radiation Shielding and Dosimetry,” John Wiley and Sons, Inc., New York, 1979.
- Y. S. Horowitz, A. Dubi and B. B. Shahar, “Self-Shielding Factors for TLD-600 and TLD-100 in an Isotropic Flux of Thermal Neutrons,” Physics in Medicine and Biology, Vol. 21, No. 6, 1976, p. 976. doi:10.1088/0031-9155/21/6/009.
- Y. S. Horowitz, A. Dubi and S. Mordechai, “Contribution of Epithermal Activation in Neutron in Vivo Activation,” Physics in Medicine and Biology, Vol. 21, No. 2, 1976, p. 306. doi:10.1088/0031-9155/21/2/015.
- Y. S. Horowitz, A. Dubi and S. Mordechai, “New Direct Point Flux Monte Carlo Estimator Using Compensated Rotational Symmetry,” Nuclear Science and Engineering, Vol. 59, No. 4, 1976, pp. 427-429.
- H. Kahn, “Applications of Monte-Carlo,” National Technical Information Service, Springfield, 1956.
- C. D. Zerby and H. S. Moran, “A Monte Carlo Calculation of the Three-Dimensional Development of HighEnergy Electron-Photon Cascade Showers,” Oak Ridge National Laboratory, Oak Ridge, 1962. doi:10.2172/4743681.
- C. D. Zerby and H. S. Moran, “Studies of the Longitudinal Development of High-Energy Electron-Photon Cascade Showers in Copper,” Oak Ridge National Laboratory, Oak Ridge, 1962.
- L. Koblinger, “Direct Sampling from the Klein-Nishina Distribution for Photon Energies above 1.4 MeV,” Nuclear Science and Engineering, Vol. 56, 1975, pp. 218- 219.
- R. N. Blomquist and E. M. Gelbard, “An Assessment of Existing Klein-Nishina Monte Carlo Sampling Methods,” Nuclear Science and Engineering, Vol. 83, No. 3, 1983, pp. 380-384.
- D. Li, C. Shaohui, H. Zhengfeng and H. Jie, “A Monte Carlo Model for Gamma-Ray Klein-Nishina Scattering Probabilities to Finite Detectors,” Journal of Nuclear Science and Technology, Vol. 33, No. 9, 1996, pp. 736-740. doi:10.3327/jnst.33.736
NOTES
*Corresponding author.

