Journal of Modern Physics
Vol.3 No.2(2012), Article ID:17695,4 pages DOI:10.4236/jmp.2012.32024
Five Dimensional Bianchi Type-I String Cosmological Models in Lyra Manifold
1Mathematics Group, BITS Pilani-K. K. Birla, Goa Campus, Goa, India
2Department of Mathematics, Ghanashyam Hemalata Institute of Technology and Management, Puri, India
Email: {gauranga1981, smruti_math}@yahoo.com
Received August 16, 2011; revised September 28, 2011; accepted October 17, 2011
Keywords: Five Dimensions; Lyra Manifold; String Cosmology
ABSTRACT
In this paper we have constructed five dimensional Bianchi type-I cosmological model generated by a cloud of string with particles attached to them in Lyra manifold. Out of the two different cases, we obtained one case leads to the five dimensional vacuum universe in Lyra manifold while the other case yields a string cosmological model in Lyra manifold. Some physical and geometrical properties of the models are briefly discussed.
1. Introduction
Now a day cosmologists are interested to study cosmic strings in the framework of general theory of relativity as well as in alternative theory. Since the discovery of general theory of relativity by Einstein, there has been numerous modification of it. Lyra [1] proposed a modification of Riemannian geometry by introducing a gauge function in to the structure less manifold that bears close resemblances to Weyl’s [2] geometry. Subsequent investigations were done by several authors Sen [3], Sen and Dunn [4], Halford [5], Bhamra [6], Beesham [7], Soleng [8], Pradhan et al. [9], Agarwal et al. [10] in scalar tensor theory and cosmology within the framework of Lyra geometry. Singh and Singh [11-13] and Singh and Desickan [14] have studied Bianchi type-I, III, Kantowski-Sachs cosmological models with time dependent displacement field in the cosmological theory based on Lyra’s manifold. Soleng [8] has pointed out that the cosmologies based on Lyra’s geometry based with constant gauge vector 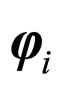 will either introduce creation field and be equal to Holy’s creation field cosmology or contain a special vacuum field which together with the gauge vector term may be considered as a cosmological term.
will either introduce creation field and be equal to Holy’s creation field cosmology or contain a special vacuum field which together with the gauge vector term may be considered as a cosmological term.
The concept of string theory was developed to describe events at the early stages of the evolution of the universe. So strings are important in the early stages of evolution of the universe before the particle creation. The present day observations do not rule out the possible existence of large scale networks of string in the early universe. Gauge theories with spontaneous symmetry breaking in elementary particle physics have given rise to anopontensive study of cosmic strings. It appears that after big bang the universe may have experienced a number of phase transitions Linde [15]. These phase transitions can produce vacuum domain structures such as domain walls, string and monopoles Kibble [16], Zel’dovich [17] of all these cosmological structures, cosmic strings have excited perhaps the most interest. Cosmic strings may act as gravitational lenses Vilenkin [18,19] and may give rise to density perturbations leading to formation of galaxies. Kibble [20] mentioned that the presence of strings in the early universe can be explained using grand unified theories. These are two major fields that the string theory ought to illuminate some day; particle physics and cosmology. Particle physics addresses the microscopic extreme while cosmology the microscopic extreme. Relativists and particle theorists have both identified the important problem of reconciling quantum theory with general relativity. The prospect of achieving this attracts both of them to string theory.
The unification of gravitational forces with other forces in nature is not possible in the usual four dimensional space times. So higher dimensional theory might be useful at very early stages of the evolution of the universe. In fact, as time evolves, the standard dimensions expand while the extra dimensions shrink to the Planckian dimension, which is beyond our ability to detect with the currently available experimental facilities Chatterjee et al. [21]. This fact has attracted many researchers to investigate the problems in the field of higher dimensions Appelquist et al. [22], Chodos and Detweller [23] constructed massive string cosmological model in higher dimensional homogeneous space time in general relativity. Krori et al. [24] constructed a Bianchi type-I string cosmological model in higher dimensional space time and obtained that matter and string coexist throughout the evolution of the universe. Venkateswarlu and Pavan Kumar [25] constructed higher dimensional string cosmological model in scale covariant theory of gravitation. Rahaman et al. [26] obtained exact solutions of the field equations for five dimensional space time in Lyra manifold when the source of gravitation is a massive string. Moanty and Samanta [27] constructed five dimensional axially symmetry string cosmological models with bulk viscous fluid In general theory of relativity. Recently Khadekar and Shelote [28] studied five dimensional FRW cosmological models with quark and strange quark matter. In this paper we constructed five dimensional Bianchi type-I string cosmological models in Lyra manifold.
2. The Metric and Field Equations
The five dimensional Bianchi type-I metric can be written as
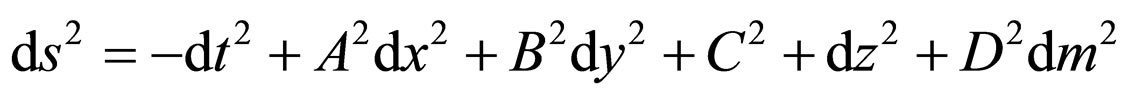 (1)
(1)
where A, B, C and D are function of cosmic time “t” only. Here the extra co-ordinate is taken to be space like.
The Einstein’s field equations based on Lyra manifold is proposed by Sen [3] and Sen and Dunn [4] in normal gauge may be written as
 (2)
(2)
where 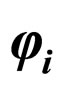 is the displacement vector and other symbols have their usual meanings as in the Riemannian geometry. The displacement vector
is the displacement vector and other symbols have their usual meanings as in the Riemannian geometry. The displacement vector 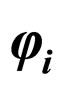 is taken in the form
is taken in the form
 (3)
(3)
The energy momentum tensor for a cosmic string is taken as
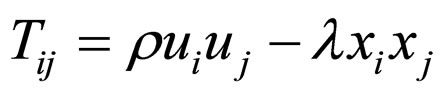 (4)
(4)
where 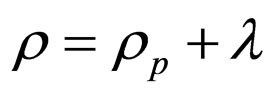 is the rest energy density of cloud of strings with particle attached to them,
is the rest energy density of cloud of strings with particle attached to them, 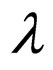 is the tension density of strings,
is the tension density of strings, 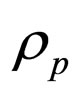 is the rest energy density of the particles,
is the rest energy density of the particles, 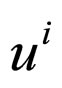 is the five velocity of particles and
is the five velocity of particles and
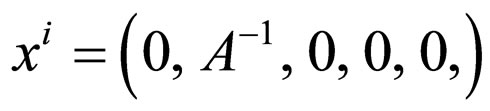 (5)
(5)
the direction of the string satisfies
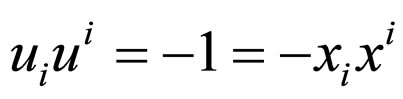 (6)
(6) 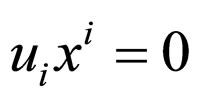
The field Equation (2) together with Equations (3)-(6) for the metric (1) yield the following equations
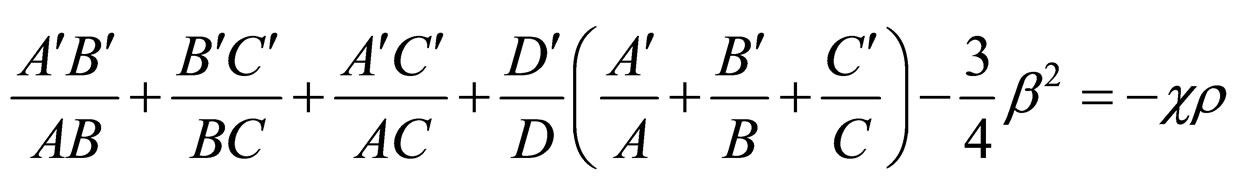 (7)
(7)
 (8)
(8)
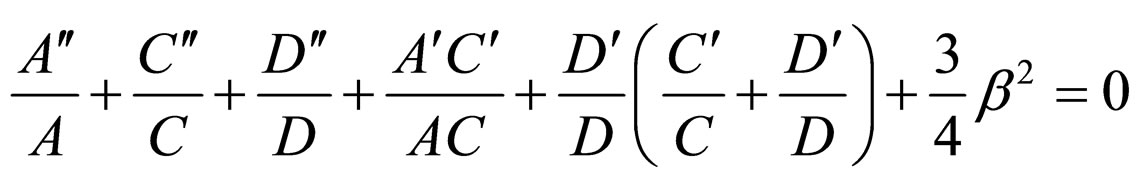 (9)
(9)
 (10)
(10)
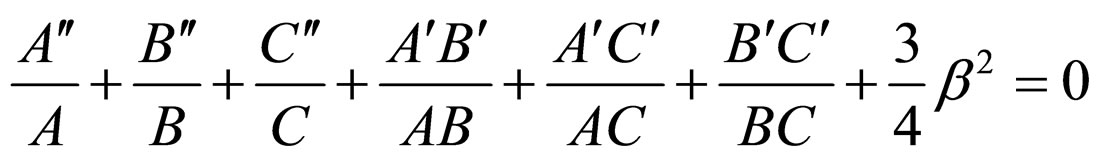 (11)
(11)
where dash denotes the differentiation with respect to “t”.
3. Cosmological Solutions
In this section we find physically meaningful solutions of the field Equations (7)-(11) by taking some simplifying assumptions.
As there is no independent equation for the gauge function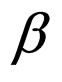 , so here we consider
, so here we consider
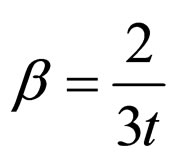 (12)
(12)
is the most suitable form to fit the observations.
3.1. Case-I (Isotropic Model)
Let
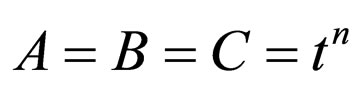 (13)
(13)
and
 (14)
(14)
where n and 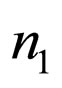 are arbitrary constants. By making use of Equations (12)-(14) in the field Equations (7)-(11) we get
are arbitrary constants. By making use of Equations (12)-(14) in the field Equations (7)-(11) we get
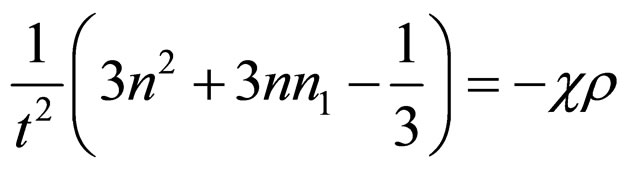 (15)
(15)
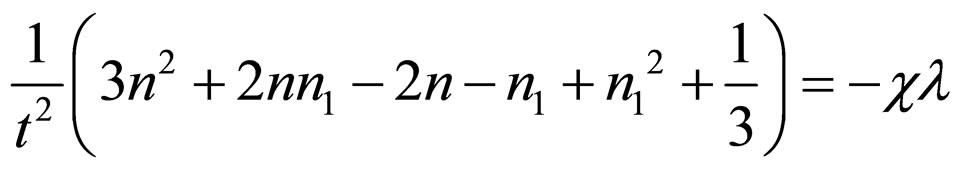 (16)
(16)
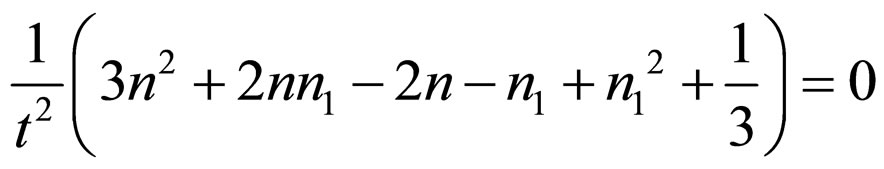 (17)
(17)
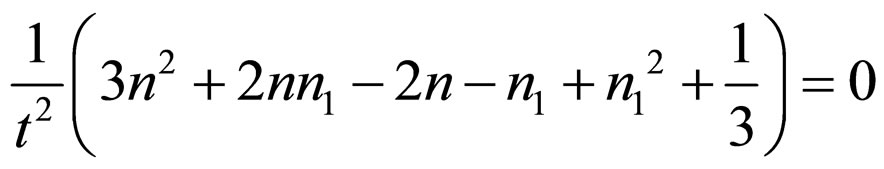 (18)
(18)
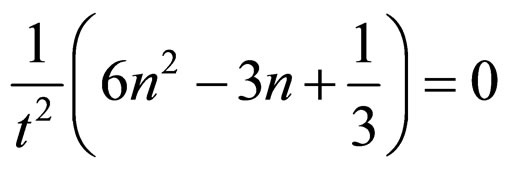 (19)
(19)
From Equation (19) we get n = 1/3 or n = 1/6 For n = 1/3 Using n = 1/3 in Equation (18) we obtained n1 = 0 or n1 = 1/3 For n = 1/6 Using n = 1/6 in Equation (18) we obtained n1 = 1/2 or n1 = 1/6 Equations (13) and (14) show that the universe expand indefinitely as t increases if n > 0 and the extra dimension contract to a Planckian length as 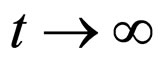 if
if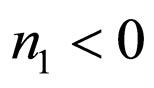 . Hence to get a physically realistic string cosmological model, we take n = 1/3 and n1 = 0.
. Hence to get a physically realistic string cosmological model, we take n = 1/3 and n1 = 0.
The geometry of the model described by the metric
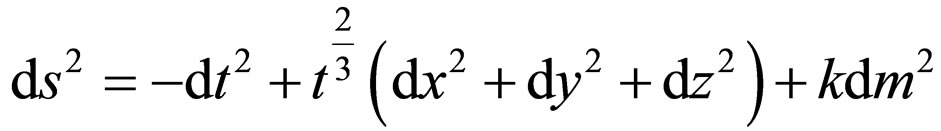 (20)
(20)
Now using n = 1/3 and n1 = 0 in Equations (15) and (16) we get
 (21)
(21)
 (22)
(22)
This shows that string does not survive for isotropic model in Lyra geometry.
The scalar expansion 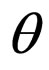 is obtained as
is obtained as
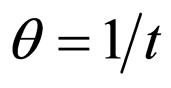 (23)
(23)
At initial epoch t = 0,  and
and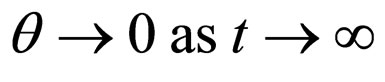 .
.
The shear scalar is obtained as
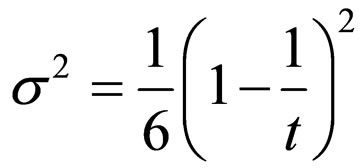 (24)
(24)
The spatial volume of the universe is obtained as
V = kt (25)
The deceleration parameter (q) is obtained as
q = 0 (26)
It is observed that the deceleration parameter “q” is identically equal to zero, earlier discussed by Venkateswarlu and Pavan Kumar [25].
3.2. Case-II (Anisotropic Model)
In this case we take
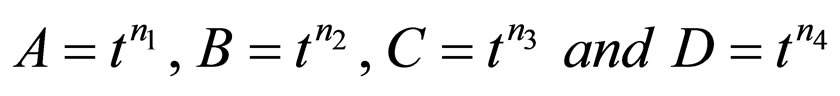 (27)
(27)
where 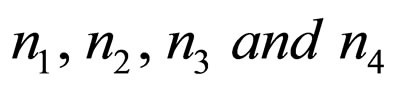 are arbitrary constants.
are arbitrary constants.
Now from Equations (7) and (8), by the use of Equations (12) and (27) we find
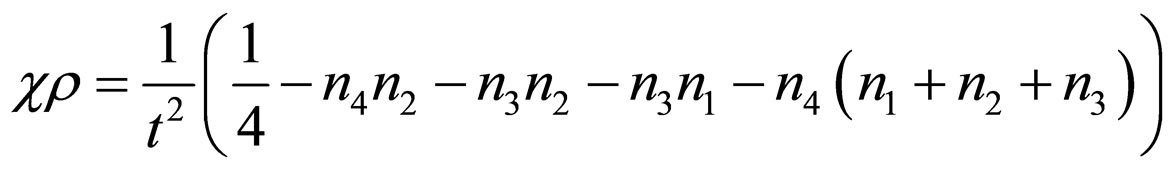 (28)
(28)
 (29)
(29)
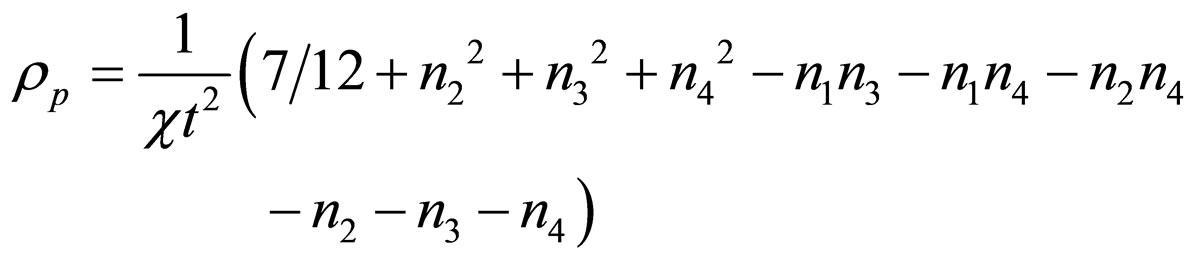 (30)
(30)
The rest energy density ( ) is given by Equation (28). It is observed that at initial epoch i.e. t = 0,
) is given by Equation (28). It is observed that at initial epoch i.e. t = 0,  ,
, 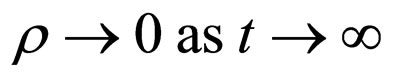 and
and  satisfies the reality condition when
satisfies the reality condition when
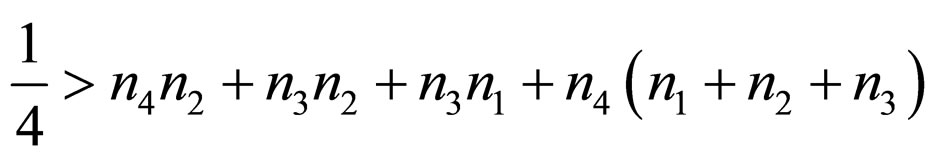
The string tension density (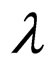 ) given by Equation (29) tends to zero as t tends to infinity. The particle density (
) given by Equation (29) tends to zero as t tends to infinity. The particle density (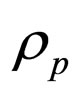 ) given by Equation (30) satisfy the reality condition when
) given by Equation (30) satisfy the reality condition when
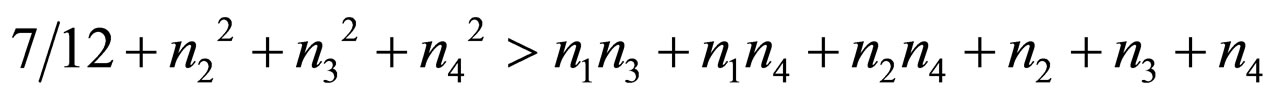
We observe that, the anisotropic three space will expand as 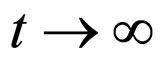 when
when  are all positive and the extra dimension will contract as
are all positive and the extra dimension will contract as 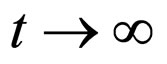 if
if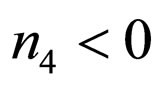 . By making use of the solutions given by Equations (27)- (29) in the field Equations (9)-(11), we conclude that
. By making use of the solutions given by Equations (27)- (29) in the field Equations (9)-(11), we conclude that
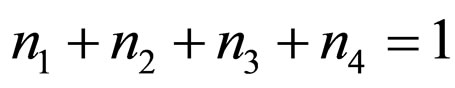
The geometry of the model described by the metric
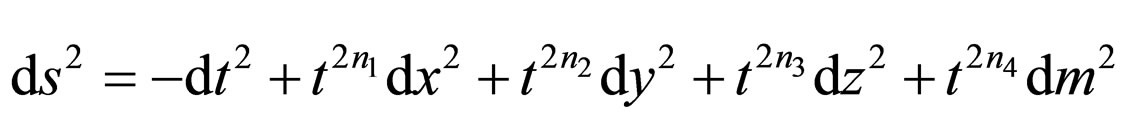 (31)
(31)
The scalar expansion (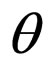 ), the shear (
), the shear (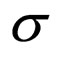 ), the spatial volume (V) and the deceleration parameter (q) for the model (31) are obtained as
), the spatial volume (V) and the deceleration parameter (q) for the model (31) are obtained as
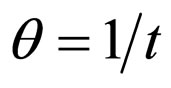 (32)
(32)
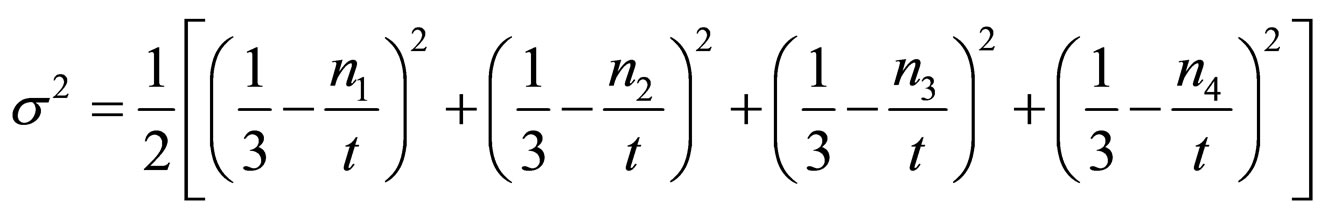 (33)
(33)
V = t (34)
q = 0 (35)
(Venkateswarlu and Pavan Kumar [25])
4. Conclusions
In this paper we constructed five dimensional Bianchi type-I cosmological models in the framework of Lyra geometry in the context of cosmic strings. From Case-I it is observed that, the isotropic Bianchi type-I higher dimensional cosmic strings do not survive. Hence we obtained higher dimensional vacuum isotropic Bianchi type-I string cosmological model in Lyra geometry. Further we observed that, the three spatial co-ordinates expand indefinitely as  while the extra dimension remains constant. It is also interesting to note that, the deceleration parameter (q) is identically equal to zero. Although the solutions obtained are special in nature.
while the extra dimension remains constant. It is also interesting to note that, the deceleration parameter (q) is identically equal to zero. Although the solutions obtained are special in nature.
From Case-II we obtained five dimensional anisotropic Bianchi type-I string cosmological model. At initial epoch i.e. t = 0, the rest energy density, tension density, particle density, scalar expansion and shear become infinity. Therefore we can say that, the model admit initial singularity. The spatial volume (V) becomes zero at t = 0 and this shows the expansion of the model with time . It is also interesting to note that, the deceleration parameter (q) is identically equal to zero.
. It is also interesting to note that, the deceleration parameter (q) is identically equal to zero.
5. Acknowledgement
The authors are extremely grateful to the referees for their valuable suggestions.
REFERENCES
- G. Lyra, “"Uber eine Modifikation der Riemannschen Geometrie,” Mathematische Zeitschrift, Vol. 54, No. 1, 1951, pp. 52-64. doi:10.1007/BF01175135
- H. Weyl, “Sber Preuss,” Academy Wiss, Berlin, 1918, pp. 465.
- D. K. Sen, “A Static Cosmological Model,” Zeitschrift für Physik A Hadrons and Nuclei, Vol. 149, No. 3, 1957, pp. 311-323.
- D. K. Sen and K. A. Dunn, “A Scalar-Tensor Theory of Gravitation in a Modified Riemannian Manifold,” Journal of Mathematical Physics, Vol. 12, 1971, pp. 578-586. doi:10.1063/1.1665623
- W. B. Halford, “Scalar-Tensor Theory of Gravitation in a Lyra Manifold,” Journal of Mathematical Physics, Vol. 13, No. 11, 1972, pp. 1699-1704. doi:10.1063/1.1665894
- K. S. Bhamra, “A Cosmological Model of Class One in Lyra’s Manifold,” Australian Journal of Physics, Vol. 27, No. 4, 1974, pp. 541-547.
- A. Beesham, “Vacuum Friedmann Cosmology Based on Lyra’s Manifold,” Astrophysics and Space Science, Vol. 127, No. 1, 1986, pp. 189-191. doi:10.1007/BF00637776
- H. H. Solenj, “Cosmologies Based on Lyra’s Geometry,” General Relativity and Gravitation, Vol. 19, No. 12, 1988, pp. 1213-1216. doi:10.1007/BF00759100
- A. Pradhan, H. Amirhashchi and H. Zainuddin, “A New Class of Inhomogeneous Cosmological Models with Electromagnetic Field in Normal Gauge for Lyra’s Manifold,” International Journal of Theoretical Physics, Vol. 50, No. 1, 2011, pp. 56-69. doi:10.1007/s10773-010-0493-0
- S. Agarwal, R. K. Pandey and A. Pradhan, “LRS Bianchi Type II Perfect Fluid Cosmological Models in Normal Gauge for Lyra’s Manifold,” International Journal of Theoretical Physics, Vol. 50, No. 1, 2011, pp. 296-307. doi:10.1007/s10773-010-0523-y
- T. Singh and G. P. Singh, “Bianchi Type-I Cosmological Models in Lyra’s Geometry,” Journal of Mathematical Physics, Vol. 32, No. 9, 1991, pp. 2456-2458. doi:10.1063/1.529495
- T. Singh and G. P. Singh, “Some Cosmological Models with Constant Deceleration Parameter,” IL Nuovo Cimento, Vol. 106, No. 6, 1991, pp. 617-622. doi:10.1007/BF02813228
- T. Singh and G. P. Singh, “Bianchi Type-III and Kantowski-Sachs Cosmological Models in Lyra’s Geometry,” International Journal of Theoretical Physics, Vol. 31, 1992, pp. 1433-1446. doi:10.1007/BF00673976
- G. P. Singh and K. Desikan, “A New Class of Cosmological Models in Lyra Geometry,” Pramana Journal of Physics, Vol. 49, No. 2, 1997, pp. 205-212. doi:10.1007/BF02845856
- A. D. Linde, “Phase Transitions in Gauge Theories and Cosmology,” Reports on Progesss in Physics, Vol. 42, No. 3, 1979, p. 389. doi:10.1088/0034-4885/42/3/001
- T. W. B. Kibble, “Some Implications of a Cosmological Phase Transition,” Physics Reports, Vol. 67, No. 1, 1980, pp. 183-199. doi:10.1016/0370-1573(80)90091-5
- Y. B. Zel’dovich, Monthly Notices of the Royal Astronomical Society, Vol. 192, 1980, p. 663.
- A. Vilenkin, “Cosmological Density Fluctuations Produced by Vacuum Strings,” Physical Review Letters, Vol. 46, 1981, pp. 1169-1172. doi:10.1103/PhysRevLett.46.1169
- A. Vilenkin, “Gravitational Beld of Vacuum Domain Walls and Strings,” Physical Review D, Vol. 28, No. 4, 1981, p. 852. doi:10.1103/PhysRevD.23.852
- T. W. B. Kibble, “Topology of Cosmic Domains and Strings,” Journal of Physics A, Vol. 9, No. 8, 1976, p. 1387. doi:10.1088/0305-4470/9/8/029
- S. Chatterjee, B. Bhui and A. Banerjee, “Higher Dimensional Cosmological Model with Homogeneous Perfect Fluid,” Physics Letters A, Vol. 149, No. 2-3, 1990, pp. 91-94. doi:10.1016/0375-9601(90)90531-R
- T. Appelquist, A. Chodos and P. G. O. Freund, “Modern Kaluza Klein Theories,” Addison Wesley, Boston, 1987.
- A. Chodos and S. Detweller, “Where Has the Fifth Dimension Gone?” Physical Review D, Vol. 21, No. 8, 1980, p. 2167. doi:10.1103/PhysRevD.21.2167
- K. D. Krori, T. Chaudhuri and C. R. Mahanta, “Strings in Some Bianchi Type Cosmologies,” General Relativity and Gravitation, Vol. 26, No. 3, 1994, pp. 265-274. doi:10.1007/BF02108006
- R. Venkateswarlu and K. Pavankumar, “Higher Dimensional String Cosmologies in Scale-Covariant Theory of Gravitation,” Astrophysics and Space Science, Vol. 298, No. 3, 2005, pp. 403-408. doi:10.1007/s10509-005-5830-z
- F. Rahaman, S. Chakraborty, S. Das, M. Hossain and J. Bera, “Higher-Dimensional String Theory in Lyra Geometry,” Pramana Journal of Physics, Vol. 60, No. 3, 2003, pp. 453-459. doi:10.1007/BF02706151
- G. Mohanty and G. C. Samanta, “Five Dimensional Axially Symmetric String Cosmological Models with Bulk Viscous Fluid,” International Journal of Theoretical Physics, Vol. 48, No. 8, 2009, pp. 2311-2318. doi:10.1007/s10773-009-0020-3
- G. S. Khadekar and R. Shelote, “Higher Dimensional Cosmological Model with Quark and Strange Quark Matter,” International Journal of Theoretical Physics, 2011. http://www.springerlink.com/content/468p520323284k2w/

