Journal of Modern Physics
Vol.2 No.11(2011), Article ID:8632,5 pages DOI:10.4236/jmp.2011.211159
Magnetic Studies of Spin Wave Excitations in Ni/Cu Multilayers
1Laboratoire de Mécanique, Productique et Génie Industriel (LMPGI), Ecole Superieure de Technologie, Université Hassan II, Casablanca, Maroc
2Laboratoire de Physique des Matériaux, Micro-Electronique, Automatique et Thermique (LPMMAT), Faculté des Sciences Ain Chock, Université Hassan II, Casablanca, Maroc
E-mail: *ha.salhi@gmail.com
Received July 12, 2011; revised August 16, 2011; accepted September 3, 2011
Keywords: Ni/Cu Multilayer, Magnetization, Spin Wave Excitations, Exchange Interactions
ABSTRACT
The magnetic properties of Ni/Cu multilayers, prepared by the electron beam evaporation method under ultra high vacuum conditions, have been systematically studied by magnetic measurements. The temperature dependence of the spontaneous magnetization M (T) is well described by a T3/2 law. A spin wave theory has been used to explain the magnetization versus temperature. Based on this theory, the approximate values for the exchange interactions have been obtained.
1. Introduction
Magnetic multilayers with artificial periodicity constitute a topic of active investigations, both on the fundamental research level as well as on the applied one. Several experimental and theoretical studies were carried out to understand the origin of the various interactions existing in this kind of systems, in particular in the interface since it presents magnetic properties different those of bulk [1-4]. Since multilayers are inherently metastable material on a nanometer scale, the introduction of the period, the number of layers and the relative thicknesses of the magnetic layers and nonmagnetic layers in multilayers will result in many interesting properties, which are sensitive to the microstructures [5-8]. The properties of these materials are mostly governed by the surface properties and hence the interface plays an important role. The discovery of coupled magnetic behavior between layer components in various magnetic multilayer systems has led to an increased interest in two-dimensional systems. To understand how the interlayer magnetic coupling between ferromagnetic layers through nonmagnetic layers affects the magnetic dynamics of such a coupled magnetic system, we carried out an investigation on a multilayer system. Furthermore, due to the immiscibility of Cu and Ni, the Ni/Cu system is an excellent one to investigate with nearly ideal artificially structures Ni/Cu multilayers with flat and sharp layer interfaces are possible using the electron beam evaporation.
In this paper we study the properties of spin waves in Ni/Cu multilayers prepared by evaporation under ultra high vacuum conditions. The comparison between the calculated and experimental magnetization enabled us to make a satisfactory estimate of the various exchange integral values.
2. Experimental
Ni/Cu multilayer was grown by evaporation in ultrahigh vacuum under controlled conditions using several electron guns. The pressure during the film deposition was maintained in the range 3 - 5 × 10–9 Torr. The deposition rate (about 0.3 Å/s) and the final thickness were monitored by precalibrated quartz oscillators. All the samples were deposited on glass substrate at 300 K on a nonmagnetic buffer layer 100 Å thick. The Ni-layer thickness tNi was varied from 14 to 50 Å and that of tCu were kept fixed at 20 Å.The number q of bi-layers were in the range 10 - 30. The x-ray diffraction in the high angle range 35˚ < 2q < 50˚ showed the existence of fcc Ni (111) peak. Magnetization M was measured using a vibrating sample magnetometer under magnetic fields up to 1T and in the temperature range 5 to 650 K.
3. Results and Discussion
The magnetization depended strongly on both the Ni and Cu layer thickness, for such thicknesses of the order of a few atomic planes. The low-temperature magnetization (per unit volume of the Ni content) was found to reach values up to about 15% higher than that of pure Ni, due to an enhancement of the Ni moment in Ni/Cu multilayer. Figure 1 shows the temperature dependence of M for several values of tNi thicknesses. It can be noticed that the Curie temperature TC decreases with decreasing Ni thickness due to reduced coordination. For three-dimensional magnetic films, the magnetization has a T3/2 dependence (for temperatures as high as TC/3) due to the classical spin-wave excitations. In such cases, according to spin-wave theory, the temperature dependence should follow the relation:
 (1)
(1)
This behavior is observed for temperatures less than TC/3.
The spin-wave constant B decreases from 86 × 10−6 K−3/2 for tNi = 14 Å to 30 × 10−6 K−3/2 for tNi = 50 Å for Ni/Cu multilayer. It is seen that B is much larger than the value of 7.5 × 10−6 K−3/2 found for bulk Ni.
The B versus 1/tNi is plotted for the samples with 14 £ tNi £ 50 Å in Figure 2. It is seen that the experimental points align well in a straight line. The values extrapolated to 1/tNi = 0 are in good agreement with those found for the bulk Ni. It was observed that the parameters B in Equation (1) depend on tNi according to:
 (2)
(2)
where B¥ is the bulk spin-wave parameter of Ni and BS is the surface spin-wave parameter value.
As the saturation magnetization decreases with decreasing layer thickness, so does the Curie temperature TC. These values of TC are much smaller than the bulk Ni value of 630 K. For ferromagnetic films the decrease of TC (tNi) as the layer thickness tNi is reduced and is usually described in the framework of finite-size scaling, which predicts in Equation (3) that TC (tNi) scales with tNi via a shift exponent λ [9]
 (3)
(3)
where C is a constant depending on the nature of the material.
The fit further results (Figure 3) in a “shift exponent”
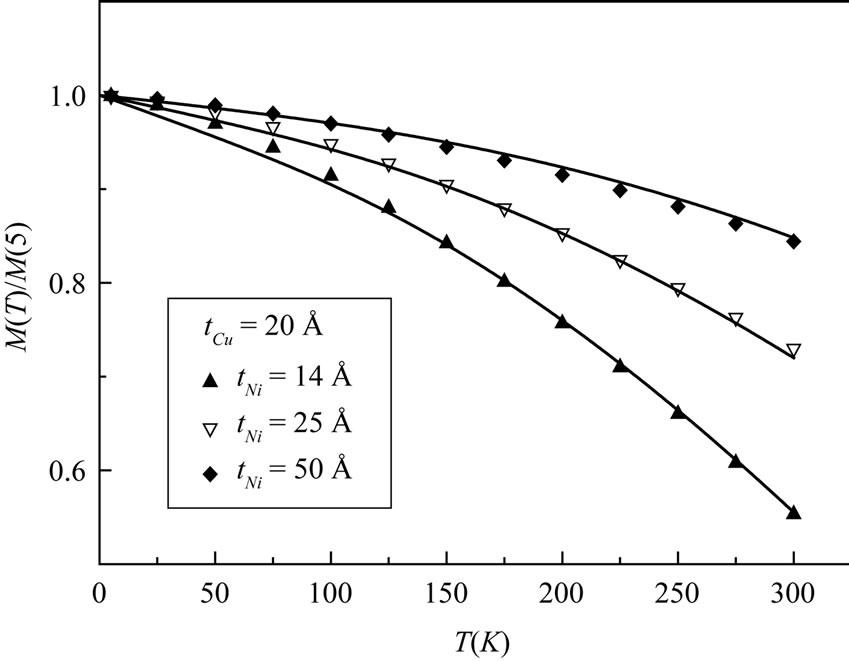
Figure 1. Calculated (continuous line) and measured (symbols) temperature dependence of the normalized magnetization of Ni/Cu multilayers versus Ni thicknesses.
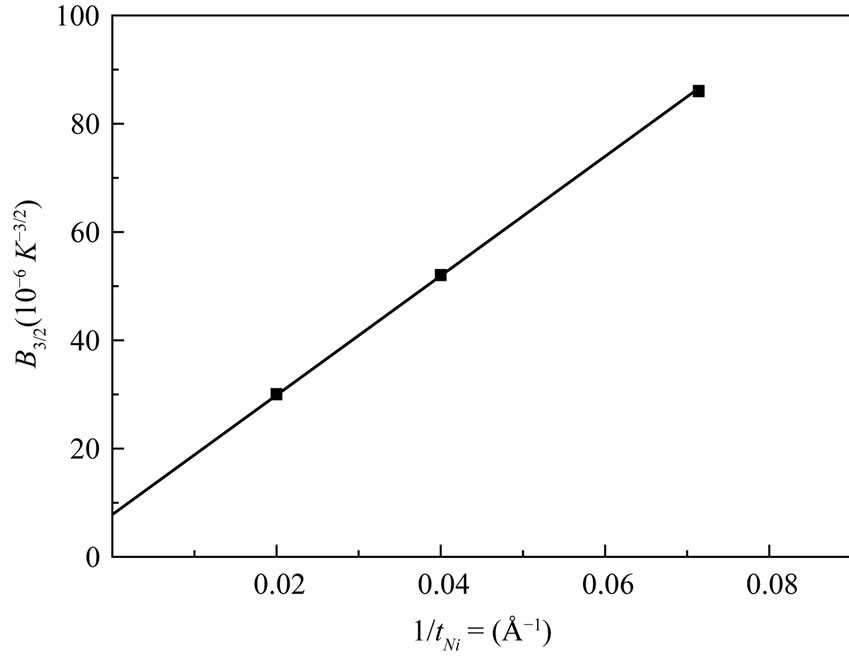
Figure 2. The spin wave constant B dependence of Ni/Cu multilayers versus inverse of Ni thicknesses.
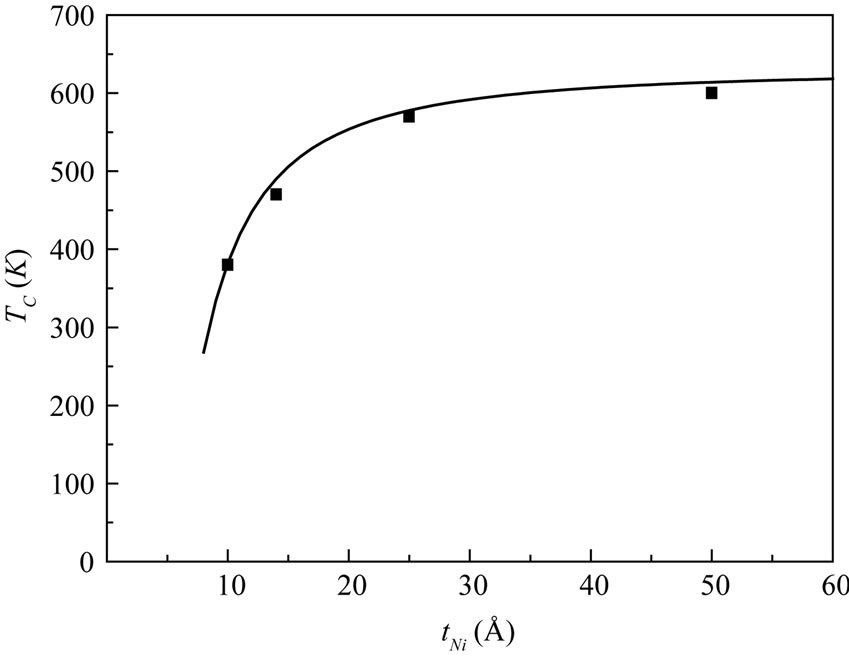
Figure 3. Curie temperature as a function of film thickness tNi.
λ = 1.7, which should be connected with the critical exponent ν of the correlation length by λ = 1/ν [9,10]; our results, obtained from multilayers, are in accordance with the value ν = 0.72 of the 3D Ising model.
To understand better how the exchange coupling between neighboring Ni layer affects the magnetic behavior of these films, we extended the model for spin waves in ferromagnetic thin films proposed by Pinnettes and Lacroix [11] to the ferromagnetic/nonmagnetic multilayers case. Here the multilayer (Xn/Ym)q is supposed to be formed by an alternate deposition of a magnetic layer (X) and nonmagnetic one (Y). The multilayer is characterized by the number q of bi-layers (X/Y), the number n of atomic planes in the magnetic layer µ and the number m of atomic planes in the nonmagnetic layer. We chose the lattice unit vectors (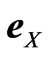 ,
, 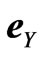 ,
,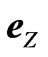 ) so that
) so that 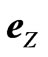 is perpendicular to the atomic planes. We note by
is perpendicular to the atomic planes. We note by ![]() the spin operator of the atom
the spin operator of the atom  in the plane
in the plane  of the magnetic layer
of the magnetic layer .
.
The system Hamiltonian is given by: H = He + Ha.
He describes the exchange interactions in the same magnetic layer (bulk and surface) as well as the exchange interactions between adjacent magnetic layers:
 (4)
(4)
where Jb and JS are the bulk and surface exchange interactions. JI is the interlayer coupling strength which depends on the number m of atomic planes in the nonmagnetic layer. The contribution of the surface anisotropy is given by:
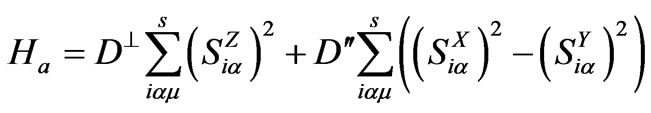 (5)
(5)
where D┴ and D// are the surface anisotropy parameters for the uniaxial out of plane and in plane componentsrespectively, and![]() .
.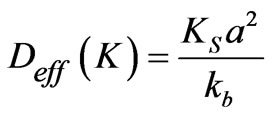 where a is the lattice constant and kb is the Boltzmann constant.
where a is the lattice constant and kb is the Boltzmann constant.
Further we denote by ΣΞ the summation on the sites of the bulk layer planes (Ξ = b), surface layer planes (Ξ = s) or the surfaces planes coupled via the nonmagnetic layer (Ξ = I). The symbol < > denotes the pairs of nearestneighbors atoms or adjacent magnetic planes.
In the Holstein-Primakoff formulation [12], the creation and annihilation operators (aiαµ and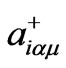 ) for each atomic spin are related to the spin operators by:
) for each atomic spin are related to the spin operators by:
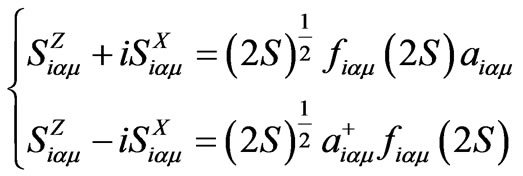 (6)
(6)
In the frame work of non interacting spin wave theory, the linear approximation of the Holstein-Primakoff method is sufficient to describe the main magnetic behavior and the correction terms are quite-small at low temperatures (T < TC/3) [3,7]. So, the value of  is fixed to 1.
is fixed to 1.
We replace the atomic variables (aiαµ, ) by the magnon variables (bkαµ,
) by the magnon variables (bkαµ, ) after a two-dimensional Fourier transformation. It gives:
) after a two-dimensional Fourier transformation. It gives:
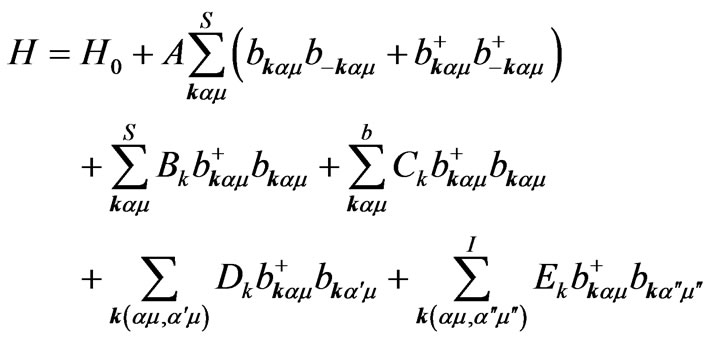 (7)
(7)
where:
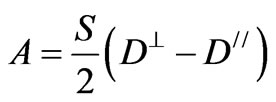
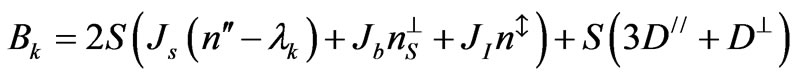
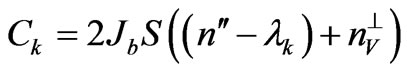
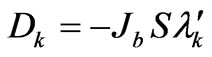

H0 is a constant term, the coefficients 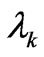 and
and 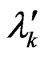 depend on the crystallographic structure of the magnetic layer. n// represents the number of nearest-neighbors sites in the same atomic plane, while
depend on the crystallographic structure of the magnetic layer. n// represents the number of nearest-neighbors sites in the same atomic plane, while 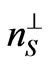 and
and 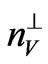 are the numbers of surface and volume nearest-neighbors in the adjacent plane in the same magnetic layer, respectively. For a given site in the surface plane of the magnetic layer, n↕ represents the number of the nearest neighbors sites in the adjacent layer across the nonmagnetic layer. For fcc (111) (
are the numbers of surface and volume nearest-neighbors in the adjacent plane in the same magnetic layer, respectively. For a given site in the surface plane of the magnetic layer, n↕ represents the number of the nearest neighbors sites in the adjacent layer across the nonmagnetic layer. For fcc (111) ( ,
,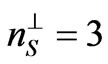 and
and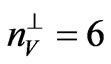 ) with the lattice constant a and in the case where the nonmagnetic layer does not disturb the succession order of the magnetic atomic planes (n↕ = 3):
) with the lattice constant a and in the case where the nonmagnetic layer does not disturb the succession order of the magnetic atomic planes (n↕ = 3):
 (8)
(8)
The motion equation is given by:
 (9)
(9)
The spin system is characterized by 2nq × 2nq equations, then the resulting secular equation:
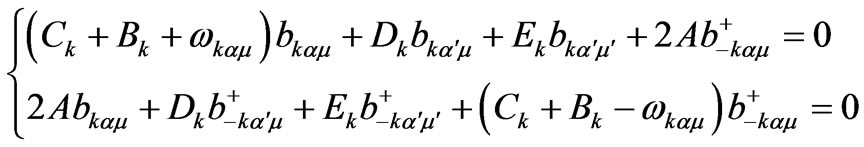 (10)
(10)
The secular equation that results from the Heisenberg equation of motion is given by 2n × 2n matrix:



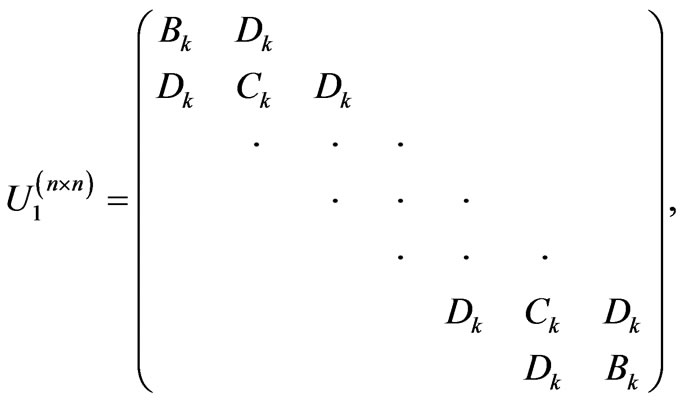
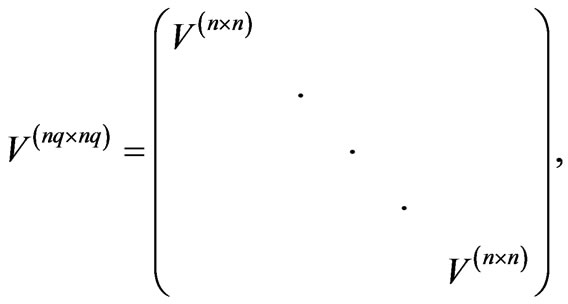
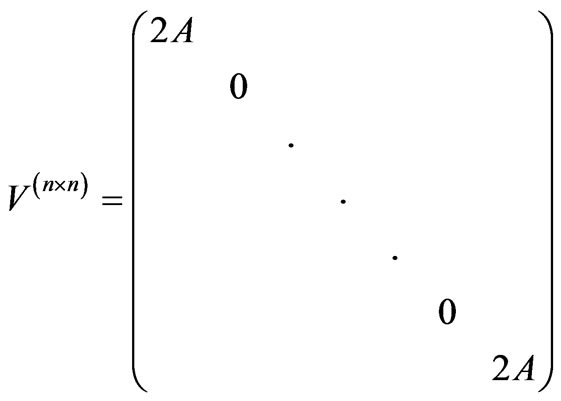

We consider the n × q positive ones which correspond to the n × q magnon excitation branches 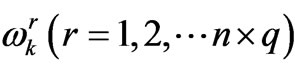 . These branches can be classified into n groups of q quasi-degenerate components in the usual case where JI remain sufficiently small compared to the effective intralayer exchange strength (Figure 4).
. These branches can be classified into n groups of q quasi-degenerate components in the usual case where JI remain sufficiently small compared to the effective intralayer exchange strength (Figure 4).
The reduced magnetization versus temperature is computed numerically from:
 (12)
(12)
The coefficient Nk indicates the number of k points taken in the first Brillouin zone.
Using Equation (12), satisfactory fits were obtained for the M (T) data for all of the Ni/Cu multilayer films. The M (T) theory curves obtained from the fits for all films are shown in Figure 1, well matching the experimental data points. Taken S = 0.3, and D┴ = 0 K, the values of Jb and JS obtained from the fits are listed in Table 1.
The derived bulk exchange interaction constants all consistently fall in the range expected for the bulk exchange interaction of Ni [3,7,13]. The interlayer coupling strength depend on the Ni thickness in the structure, the saturation magnetization (MS) of the layers and their respective fields (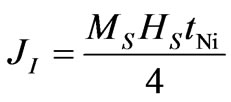 , where HS is the saturation field) [14]. Compared to the bulk exchange interaction coupling, however, the interlayer coupling is con-
, where HS is the saturation field) [14]. Compared to the bulk exchange interaction coupling, however, the interlayer coupling is con-

Figure 4. Spin-wave excitation spectrum ωk. kx (ky = kx ) for fcc (111) ferromagnetic multilayer with tNi = 14 Å, S = 0.3, JS = 77 K, Jb = 240 K, JI = 0 K, D// = 0.03 K, D┴ = 0 K; in the case: Jb/JS = 3.
) for fcc (111) ferromagnetic multilayer with tNi = 14 Å, S = 0.3, JS = 77 K, Jb = 240 K, JI = 0 K, D// = 0.03 K, D┴ = 0 K; in the case: Jb/JS = 3.

Table 1. The fitting results from Equation (12) for Ni/Cu. Jb is the bulk exchange interaction between neighboring Ni atoms and JS is the surface exchange interaction.
siderably weak. Nonetheless, its effect on the magnetic properties is rather significant. The Ni layers are coupled together by an interlayer exchange coupling, and that the spin waves extend across the whole multilayer sample. The propagation of spin waves through the Cu layers implies the existence of spin polarization within the Cu.
4. Conclusions
The temperature dependence of the magnetization has been investigated for Ni/Cu multilayer. It is seen that the spin-wave constant is much larger than the value found for bulk Ni. A simple model has allowed us to obtain numerical estimates for the exchange interactions and the interlayer coupling strength for Ni/Cu multilayer. Evidence of spin polarization of the nonmagnetic layers, related to the interlayer coupling, was obtained.
REFERENCES
- A. Ercole, “Temperature-Dependent Spin-Wave Behavior in Co/CoO Bilayers Studied by Brillouin Light Scattering,” Journal of Physical Review B, Vol. 62, No. 10, 2000, pp. 6429-6436. doi:10.1103/PhysRevB.62.6429
- A. Yoshihara, “Collective Spin Waves in an Ultrathin Fe Wedge: A Brillouin Scattering Study,” Journal of the Physical Society of Japan, Vol. 65, No. 5, 1996, pp. 1469-1474. doi:10.1143/JPSJ.65.1469
- H. Salhi, “Magnetic Studies of Spin Wave Excitations in Ni/Au Multilayers,” Journal of Physics of Condensed Matter, Vol. 405, No. 5, 2010, pp. 1312-1315. doi:10.1016/j.physb.2009.11.075
- A. Fahmi, “A Study of the Magnon Contribution to the Properties of the [Ni1−xFex/Cu] Alloy Super-Lattices,” Journal of Magnetism and Magnetic Materials, Vol. 303, No. 1, 2006, pp. 26-33. doi:10.1016/j.jmmm.2005.10.226
- X. Y. Zhu, “Microstructure and Mechanical Properties of Nanoscale Cu/Ni Multilayers,” Journal of Materials Science and Engineering, Vol. 4-5, 2010, pp. 1243-1248. doi:10.1016/j.msea.2009.09.058
- F. Wilhelm, “Layer-Resolved Magnetic Moments in Ni/Pt Multilayers,” Journal of Physical Review Letters, Vol. 85, No. 2, 2000, pp. 413-416. doi:10.1103/PhysRevLett.85.413
- K. Chafai, “Magnetic Studies in Evaporated Ni/Pd Multilayers,” Journal of Magnetism and Magnetic Materials, Vol. 323, No. 5, 2010, pp. 596-599. doi:10.1016/j.jmmm.2010.10.020
- H. Lassri, “Ferromagnetic Resonance Studies of Electrodeposited Ni/Cu Multilayers,” Journal of Thin Solid Films, Vol. 389, No. 1-2, 2001, pp. 245-249. doi:10.1016/S0040-6090(00)01920-9
- G. A. T. Allan, “Critical Temperatures of Ising Lattice Films,” Journal Physical Review B, Vol. 1, 1970, pp. 352-356. doi:10.1103/PhysRevB.1.352
- M. Abid, “Magnetic Properties of Ni/V Multilayers,” Journal of Magnetism and Magnetic Materials, Vol. 202, No. 2, 1999, pp. 335-341. doi:10.1016/S0304-8853(99)00359-5
- C. Pinettes, “Influence of Surface Anisotropy in Ferromagnetic Thin Films,” Journal of Magnetism and Magnetic Materials, Vol.166, No. 1-2, 1997, pp. 59-64. doi:10.1016/S0304-8853(96)00508-2
- T. Holstein, “Field Dependence of Intrinsic Domain Magnetization of a Ferromagnet,” Journal of Physical Review, Vol. 58, 1940, pp. 1098-1113.
- D. C. Jiles, “Introduction to Magnetism and Magnetic Materials,” Chapman and Hall, London, 1991.
- S. S. P. Parkin, “Systematic Variation of Strength and Oscillation Period Of Indirect Magnetic Exchange Coupling through the 3d, 4d and 5d Transition Metals,” Journal of Physical Review Letters, Vol. 67, 1991, pp. 3598- 3601.

