Journal of Modern Physics
Vol. 2 No. 8 (2011) , Article ID: 6676 , 9 pages DOI:10.4236/jmp.2011.28096
Early-Universe and Evolution of the Present Universe: Exact Solution Models
1Department of Mathematics, Sambalpur University, Orissa, India
2Department of Mathematics, Manipur University, Imphal, India
3Department of Mathematics, Ideal Girls’ College, (Manipur University), Imphal, India
E-mail:{drmanihar, jairamth}@rediffmail.com, pk_mathematics@yahoo.co.in
Particle Creation, Relativity
Received February 17, 2011; revised April 2, 2011; accepted May 4, 2011
Keywords: Evolution, Early Universe, Inflation, Radiation-Dominated Era, Big Bang, Phase Transition,
ABSTRACT
The evolution of the Robertson-Walker type universes consisting of radiating perfect fluid distribution coupled with zero-mass scalar field in which the gravitational parameter G varies with cosmic time t are studied. Unified descriptions of the early evolution of the universe consisting of different phases are investigated. The different properties of the cosmological solutions are discussed and the physical behaviour of the model universes during the radiation-dominated era and also during the big bang scenario are studied. Here we obtain models which are geometrically closed and are thereby ever expanding and evolve from rest from a nonsingular hot origin with maximum (finite) energy density and temperature and a small minimum (non-zero) gravitational coupling G.
1. Introduction
Though it is generally accepted that the Newtonian constant of gravity G plays the role of a coupling constant between geometry and matter in the Einstein field equations, it appears natural to look at this constant as a function of time in an evolving universe. There are extensions of Einstein’s theory of gravitation in which G is taken to vary with time [1]. In general relativity G plays the role of a coupling constant between geometry and matter in Einstein’s field equations. The value of G is to be constant, since G—constancy is in-built as a manifestation of the principle of equivalence. A breakdown from the principle of equivalence, in any form, would constitute a departure from Einstein’s general relativity. The time-dependence of G follows as a natural consequence of Dirac’s large number hypothesis [2]. The implication of time-varying G will become more important at the early stage of the evolution of the universe.
[3] studied the homogeneous and isotropic cosmological model in which the parameter gamma of “Gammalaw” equation of state p = (γ–1) ρ varies continuously with cosmic time t. He studied the evolution of the universe as it goes from an inflationary phase to a radiationdominated phase. [4] obtained a singularity-free model of the evolving universe with matter and studied the transition from the beginning to the radiation-dominated and matter-dominated periods of the universe.
Some workers studied the problem of the universe by linking the variation of G with that of the cosmological constant Λ leaving the form of the field equations unchanged and preserving the conservation of the energymomentum tensor of the matter content by [5-8]. The possibility of an increasing G was also suggested by [9]. The possibility of the creation field with G varying as some powers of t discussed by [8]. [10] also presented exact solutions for zero pressure Robertson-Walker cosmological models with G varying as some powers of R. A spatially flat FRW model wherein the vacuum energy density has been taken to vary as the radiation energy density discussed by [11,12] discussed about the effect of bulk viscosity on the early evolution of universe, [13] discussed about early universe with variable cosmological and gravitational constants in higher dimensional space time. [14,15] discussed about the cosmology of the very early universe and structures in the Universe by exact methods.
Here in this problem we study the evolution of the universe taking the Robertson-Walker models of radiating perfect fluid distribution in the presence of zero-mass scalar field in which the gravitational parameter G varies with cosmic time t. Solutions are obtained for inflationary phase and radiation-dominated phase. The physical behaviors of the cosmological solutions are discussed. Also we study the effects of incorporating a zero-mass scalar field which is operative during an instantaneous phase transition, and it is found that the presence of the scalar field is instrumental in avoiding the initial singularity and gives freedom to the choice of initial conditions, thus giving advantage of studying different scenarios. Its presence also results in particle creation and thereby influence the subsequent evolution of the universe find Robertson-Walker models starting either from a non-singular origin with a minimum, non-zero G or from a singularity with a vanishing G, where G increases continuously in the radiation dominated era and approaches a constant value as the universe turns matter-dominated, finally the models approaching the standard model. Such study of the evolution of the universe will be of great importance in revealing the many mysteries of the different astrophysical objects in general and the universe in particular.
2. Field Equations
The line element considered for this problem is
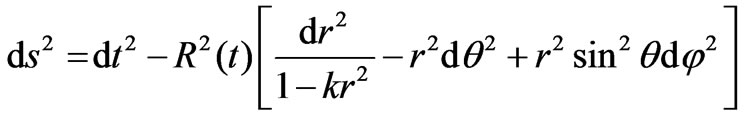 (1)
(1)
where R(t) is the scale factor and K, the curvature index which takes values +1, 0 and –1.
Considering perfect fluid distribution coupled with zero-rest mass scalar field the energy-momentum tensor takes the form
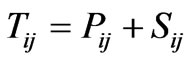 where Pij is the energy-momentum tensor due to a perfect fluid given by
where Pij is the energy-momentum tensor due to a perfect fluid given by
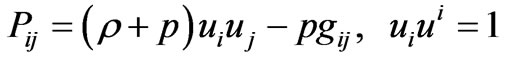 (2)
(2)
And Sij is the energy-momentum tensor due to zeromass scalar field given by
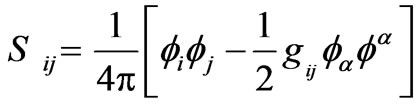 (3)
(3)
Where the scalar potential 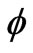 satisfies the equation
satisfies the equation
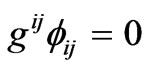 (4)
(4)
Thus from the Einstein field equation

We get
 (5)
(5)
and
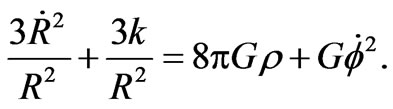 (6)
(6)
Now Equations (5) and (6) give
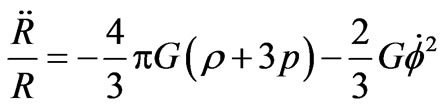 (7)
(7)
and
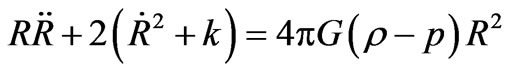 (8)
(8)
From Equation (4) we have
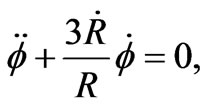
Which give us
 (9)
(9)
where 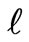 is an integration constant.
is an integration constant.
Again from Equations (7) and (8) we have, eliminating 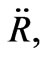
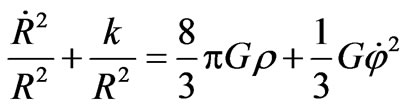 (10)
(10)
For the radiating universe we have the relation
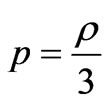 (11)
(11)
Thus Equations (8)-(10) give
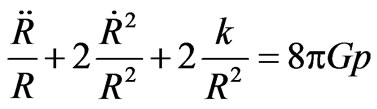 (12)
(12)
and
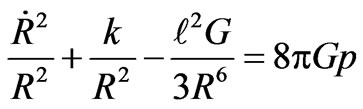 . (13)
. (13)
Now from Equations (12) and (13) we have
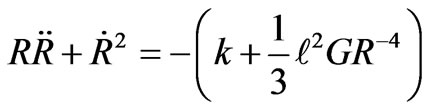 (14)
(14)
We consider underneath the different phases and scenario in the course of evolution of the universe.
Case I
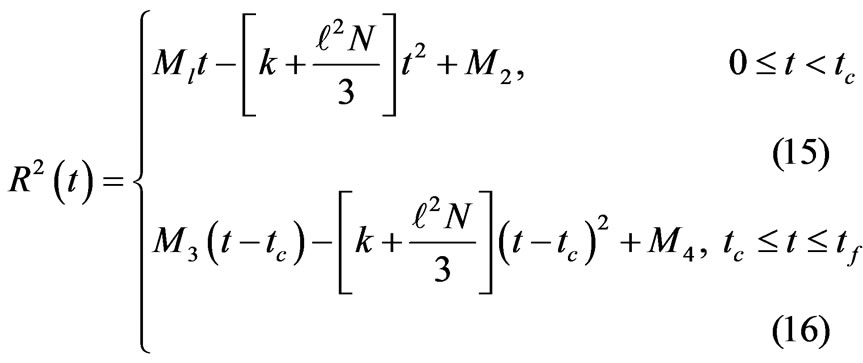 with G
with G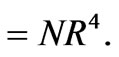 (17)
(17)
Thus we have here
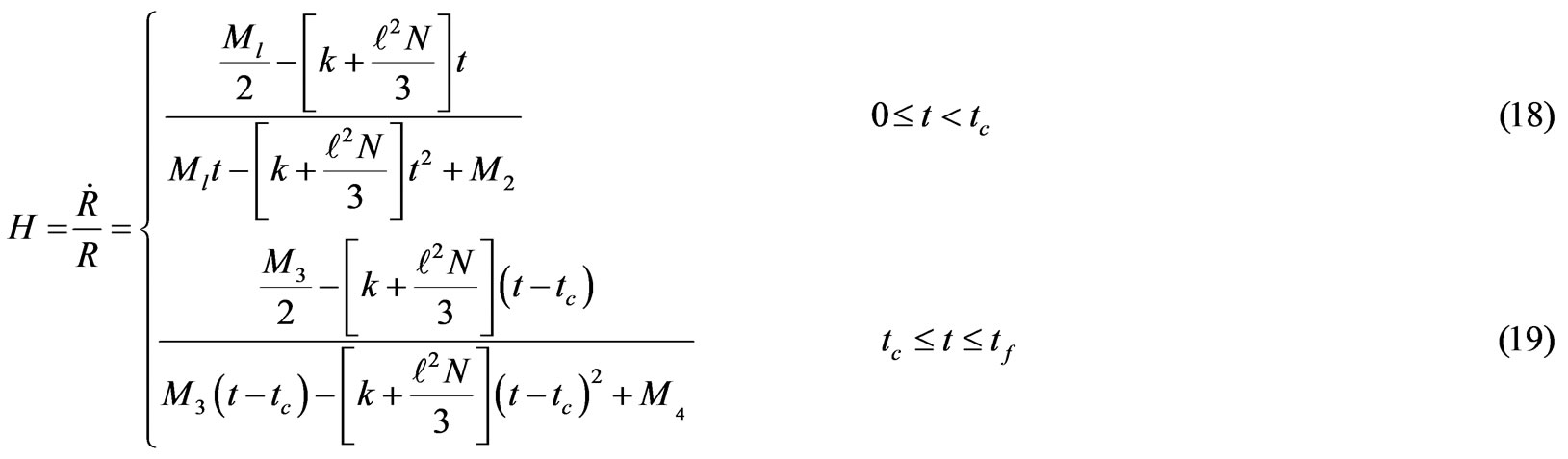
where in this paper 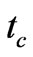 means the time at which the critical temperature occurs, that is at which a phase transition occurs and
means the time at which the critical temperature occurs, that is at which a phase transition occurs and  the time at which that particular phase ends.
the time at which that particular phase ends.
Case I (a): An Inflationary Phase
Now taking the initial condition as R = Ro at t = 0, we obtain from Equation (15)
 (20)
(20)
And from relation (18) we get
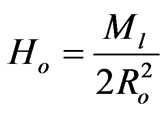 (21)
(21)
but
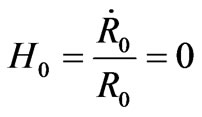 as
as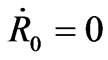 since
since 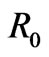 is a particular value of R at t = 0.
is a particular value of R at t = 0.
Thus Equation (10) with 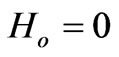 reduces to
reduces to
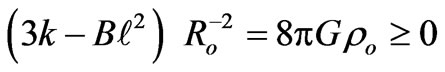
which shows that 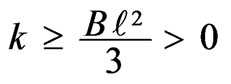 and thus k = 1.
and thus k = 1.
Therefore we get
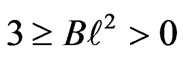 (22)
(22)
Equation (16) with the condition R(t) = Rc, at t = tc gives M4 =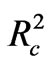 . And the continuity for R(t) across t = tc implies
. And the continuity for R(t) across t = tc implies
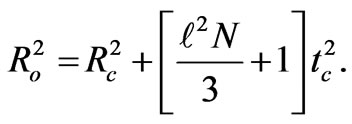 (23)
(23)
Now relations (18) and (19) give, in the limit 
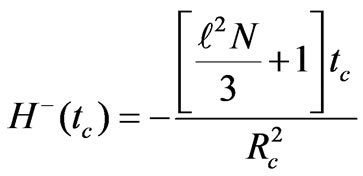 (24)
(24)
and
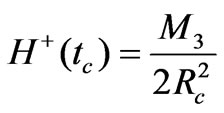 (25)
(25)
Thus the continuity in H due to phase transition, which arises due to presence of scalar field, is found to be
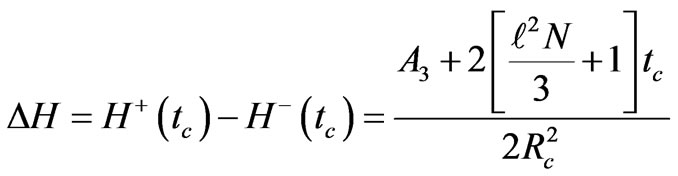 (26)
(26)
Since  H must vanish in the limit, we have
H must vanish in the limit, we have
 .
.
Hence Equations (15) and (16) reduce to (see (27)-(28)).
Equations (27)-(28) show that the expansion is endowed with a generalized inflation 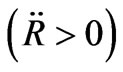 as long as
as long as 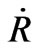 remains greater than
remains greater than
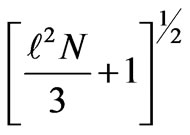
and turns deflationary as  becomes smaller than
becomes smaller than
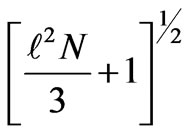 .
.
Case I (b) A Radiation—Dominated Phase
Now Equation (4) gives
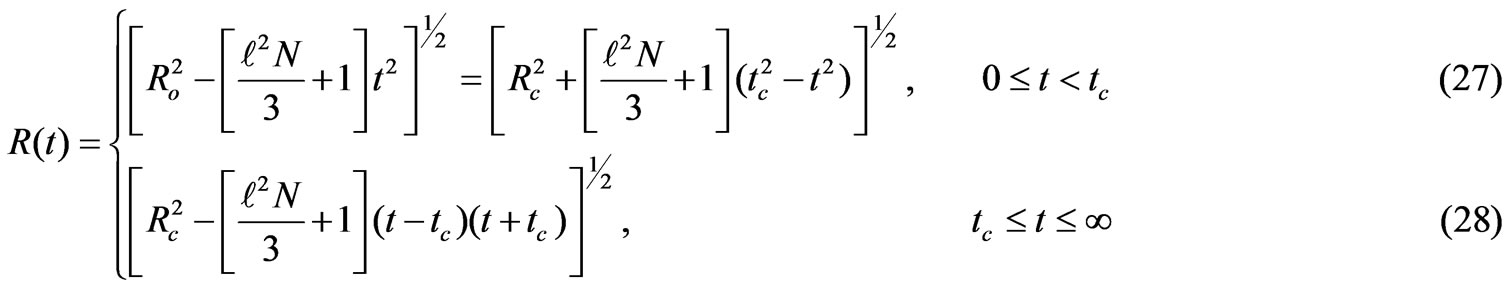
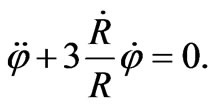 (29)
(29)
Also Equations (7) and (10) respectively give
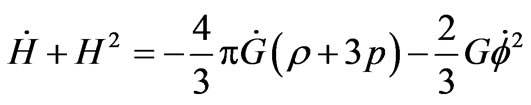 (30)
(30)
and
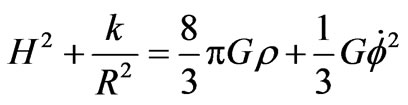 (31)
(31)
where H = 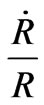 is the Hubble’s parameter.
is the Hubble’s parameter.
Thus from Equations (11) and (30) we get
 (32)
(32)
Now eliminating 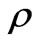 between Equations (31) and (32) we have
between Equations (31) and (32) we have
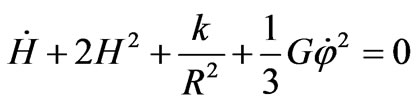 (33)
(33)
which can be rewritten as
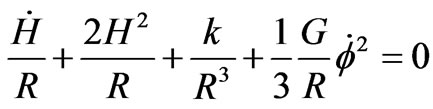
i.e. 
i.e. 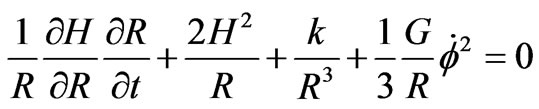
i.e. 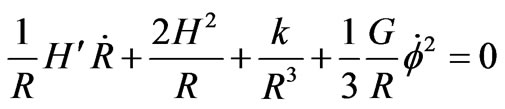
i.e. 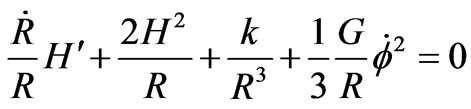
i.e.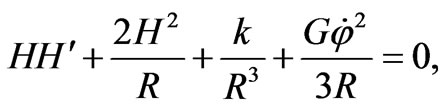 (34)
(34)
where a dash denotes differentiation w.r.t. R.
Considering zero-curvature Robertson-Walker metric, Equation (34) takes the form
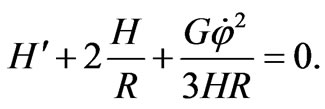 (35)
(35)
Now from relation (29) we get
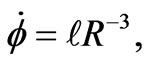 (36)
(36)
where 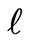 is integration constant.
is integration constant.
Making use of relation (36) in Equation (35) we get
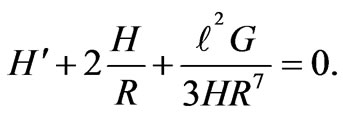 (37)
(37)
Without loss of generality we take the solution of Equation (37) as
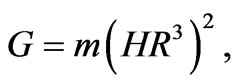 (38)
(38)
with
 (39)
(39)
where m and c are arbitrary constants.
If 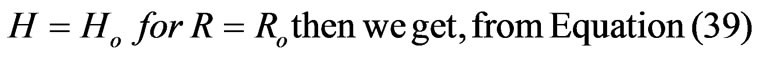
C = (40)
(40)
Thus Equation (39) takes the form
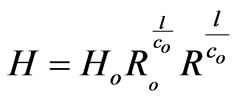 , (41)
, (41)
where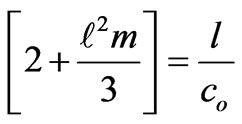 Now Equation (40) gives
Now Equation (40) gives
 (42)
(42)
Thus we have
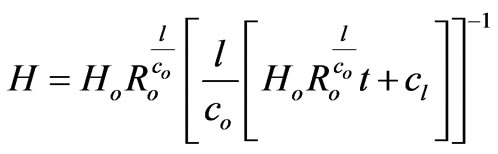 (43)
(43)
And from relations (38), (41) and (42) we get
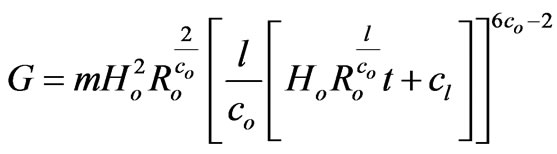 (44)
(44)
Also we have
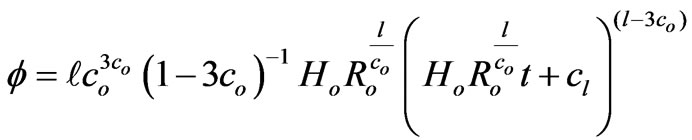 (45)
(45)
and
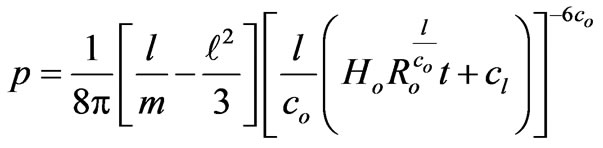 (46)
(46)
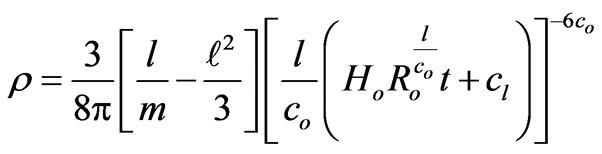 (47)
(47)
Here in this case, G is found to be an increasing function of time, whereas f is seen to be a decreasing function of time. In this phase or episode the pressure and density of the universe are found to decrease along with the increase of the cosmic age (of course, if the constants 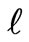 and m are so related that
and m are so related that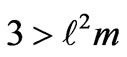 ). For this era R is seen to be an increasing function of time thus showing that during this era the universe is expanding.
). For this era R is seen to be an increasing function of time thus showing that during this era the universe is expanding.
Case II
Now another solution of Equation (14) is
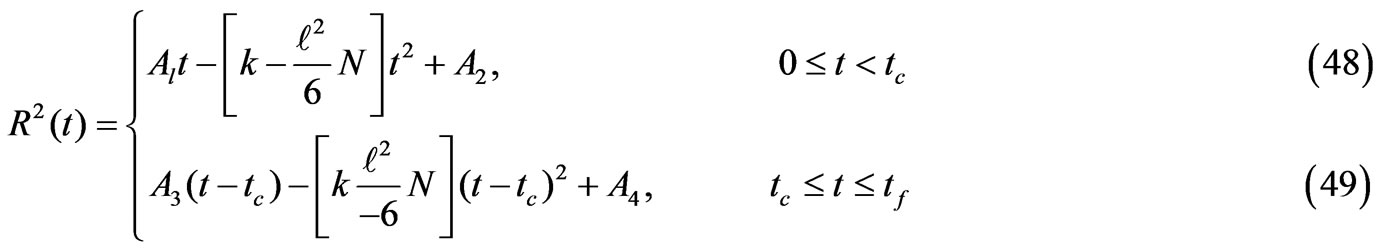
with
 (50)
(50)
This solution is quite different from the solution in Case-I; more particularly the value of G in this case is very much different from that value of G in Case-I. Thus in this case we will be getting another type of solution (universe) where the big bang scenario, the inflationary phase and the radiation-dominated phase will be quite distinct from that of the universe in Case-I.
From relations (48) and (49) we get
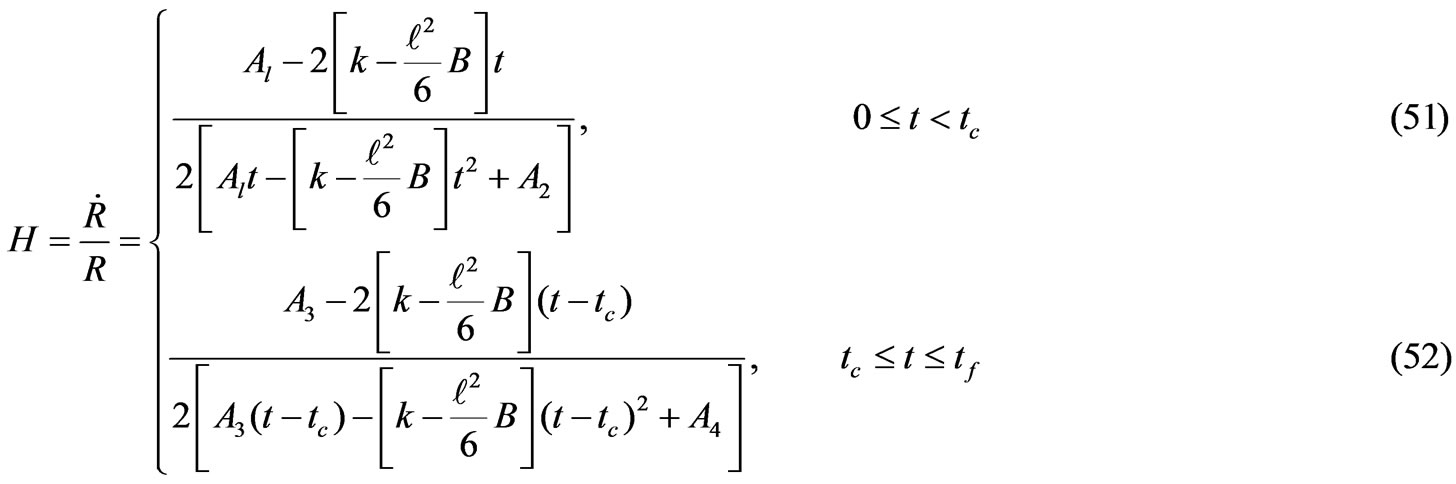
Case II (a) An Inflationary Type Solution
Taking the initial condition 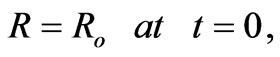 we obtain from relation (48)
we obtain from relation (48)
 (53)
(53)
And from relation (51) we get
 (54)
(54)
Equation (10) with  reduces to
reduces to
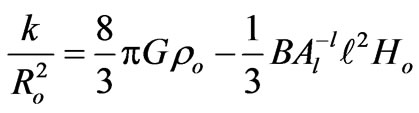
Thus 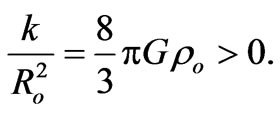 (55)
(55)
This shows that k > 0 which implies k = l.
Again Equation (49) with the condition R(t) = 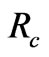 at t =
at t = 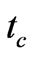 give
give .
.
And for continuity of R(t) across t =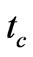 we must have
we must have
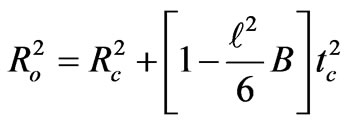 (56)
(56)
Now in the limit 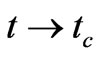 and relations (51) and (52) become
and relations (51) and (52) become
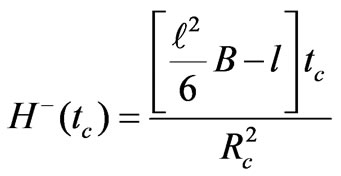 (57)
(57)
and
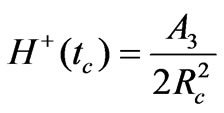 (58)
(58)
Thus the discontinuity in H due to the phase transition, which arises due to the presence of scalar field is found to be
 (59)
(59)
Now we can speculate that 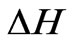 must vanish in the limit and this gives
must vanish in the limit and this gives
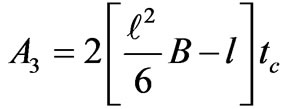 (60)
(60)
Then Equations (48) and (49) give
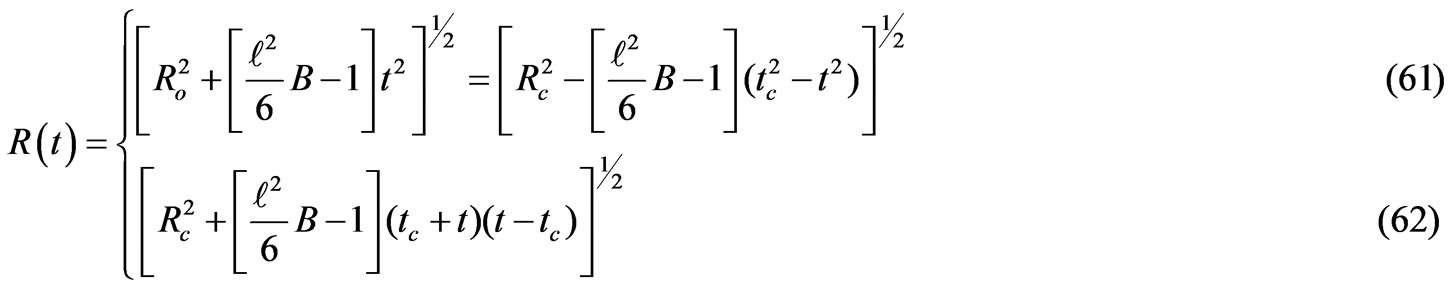
Thus showing that the expansion is endowed with a generalized inflation 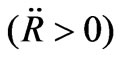 as long as
as long as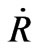 remains smaller than
remains smaller than
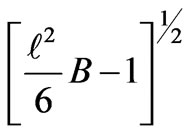
and turns deflationary as 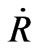 becomes larger than
becomes larger than
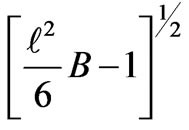
Also from Equation (61) we see that  although k = l. It may be taken as a significant deviation from the standard model which is resulted from the coupling of the scalar field.
although k = l. It may be taken as a significant deviation from the standard model which is resulted from the coupling of the scalar field.
Also in this case the radiation density is found to be
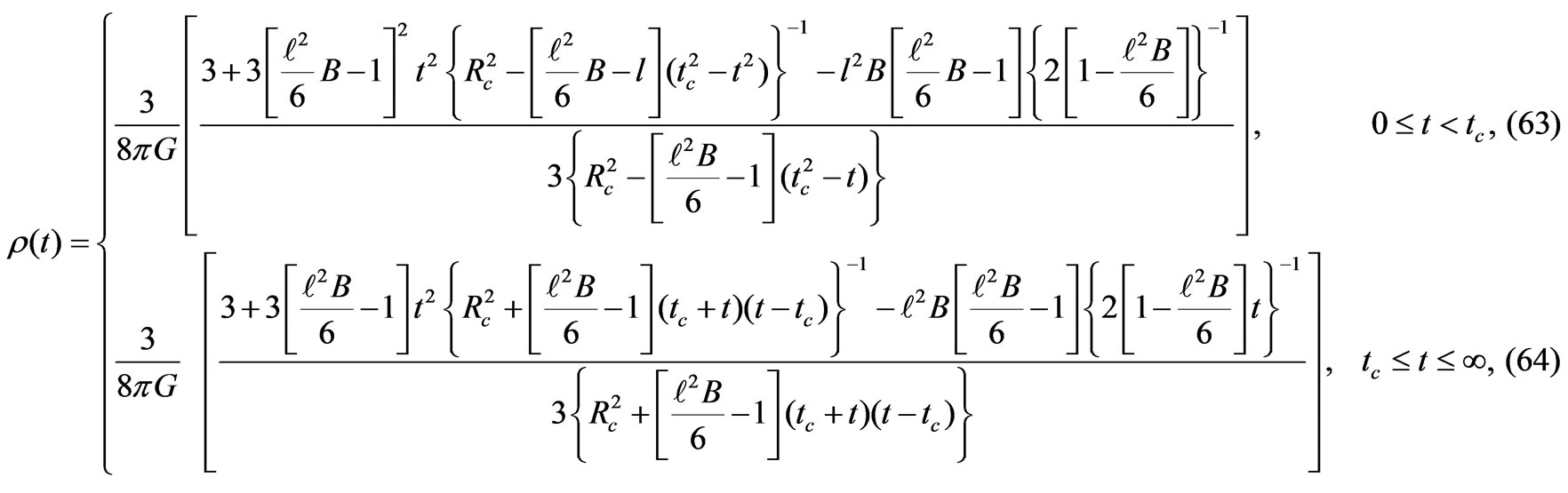
Case II (b) Big Bang Scenario
Considering the condition R(t) = 0 at t = 0 and R(t) = 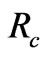 at
at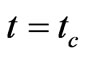 ,Equations (48) and (49) give
,Equations (48) and (49) give
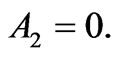 (65)
(65)
and
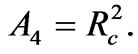 (66)
(66)
Thus for the continuity of R(t) at 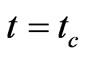 we must have
we must have
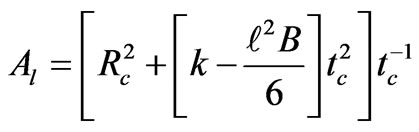 (67)
(67)
Therefore for the limit 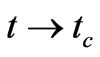 relations (51) and (52) become
relations (51) and (52) become
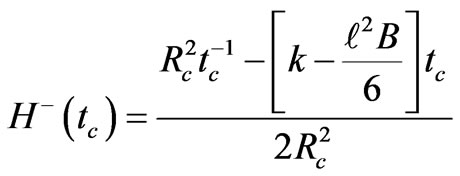 (68)
(68)
and
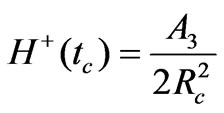 (69)
(69)
Thus the continuity in H(t) due to the phase transition follows from
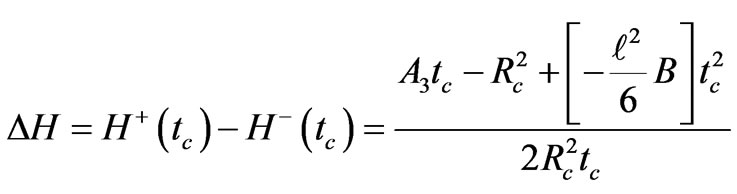 (70)
(70)
Therefore for 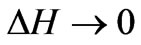 we obtain
we obtain
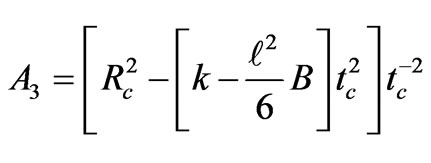 (71)
(71)
Hence we have
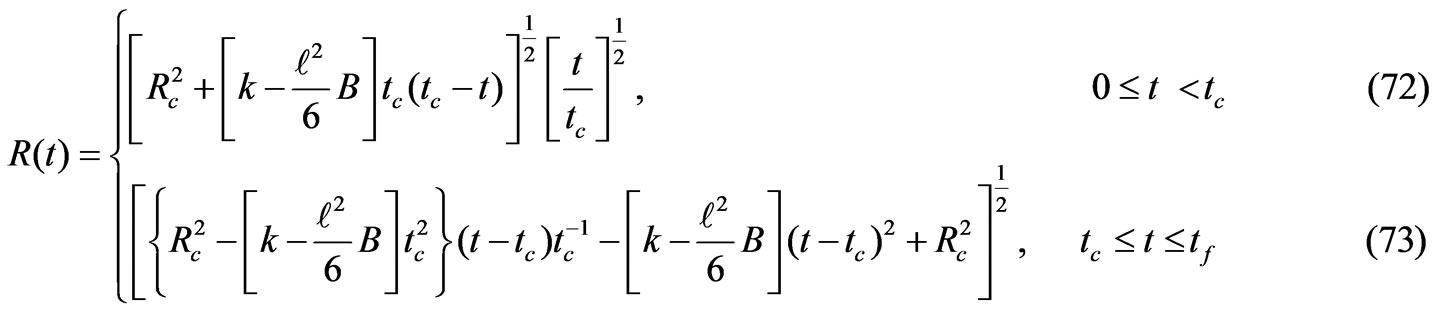
Underneath we shall study two different types of evolution one having the phase transition in the expanding phase and other in the collapsing phase depending upon whether .
.
Case II (b)*
We see from Equations (72) and (73) that the universe reaches its maximum radius at
 (74)
(74)
and
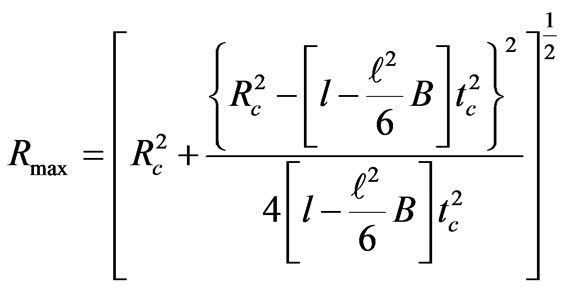 (75)
(75)
Then after that it collapses to a singularity at  give by
give by
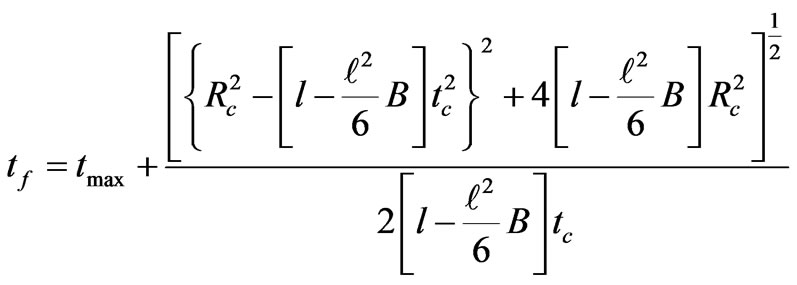 (76)
(76)
Here we see that the phase transition occurs in the expanding phase of evolution (before reaching the maximum radius) at 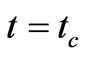 when there is a sudden rise in the rate of expansion. And the subsequent evolution is affected by the presence of the scalar field. The larger the value of
when there is a sudden rise in the rate of expansion. And the subsequent evolution is affected by the presence of the scalar field. The larger the value of 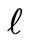 or in other words greater the strength of the scalar field the longer it will take for the universe to reach its maximum radius, and in this way the final collapse will be prolonged.
or in other words greater the strength of the scalar field the longer it will take for the universe to reach its maximum radius, and in this way the final collapse will be prolonged.
Case II (b)**
Here we take up the case
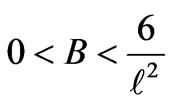 with
with .
.
In this case we see that the radius reaches a maximum before the transition takes place, as is clear from the examination of the Equations (72) and (73). This gives
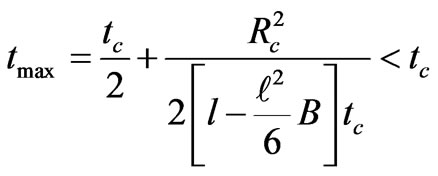 (77)
(77)
and
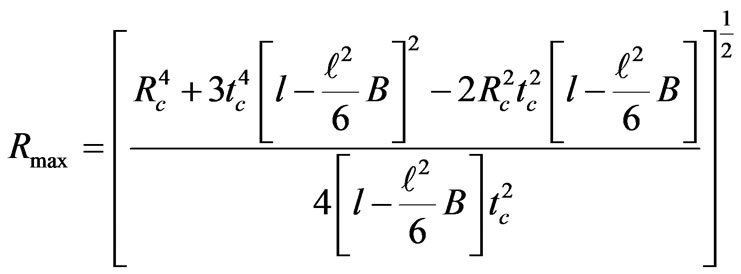 (78)
(78)
Here the universe seems to collapse to a singularity at
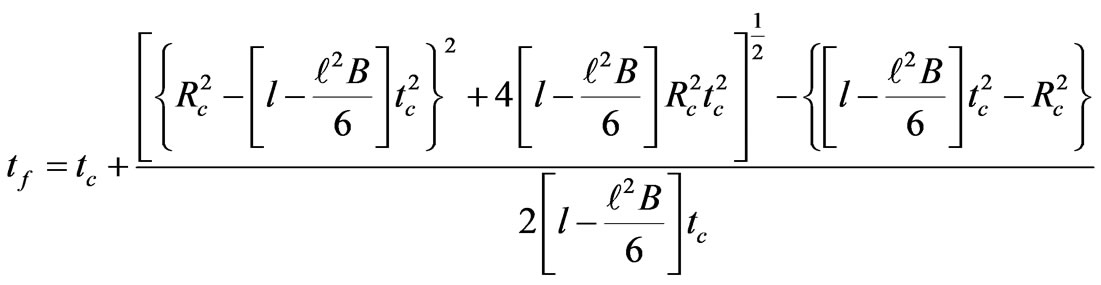 (79)
(79)
It is observed that the transition takes place in the collapsing phase of evolution 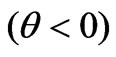 and the presence of scalar field therefore adds to the hydrostatic pressure (as
and the presence of scalar field therefore adds to the hydrostatic pressure (as 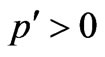 in the collapsing phase), and thereby to the inertial effects which make the universe to collapse back to singularity at a faster rate as clear from Equation (70).
in the collapsing phase), and thereby to the inertial effects which make the universe to collapse back to singularity at a faster rate as clear from Equation (70).
Moreover, the time variation of energy density in the different models may be obtained from Equation (10) by using the time dependence of the functions R(t) and H(t).
Thus we have here
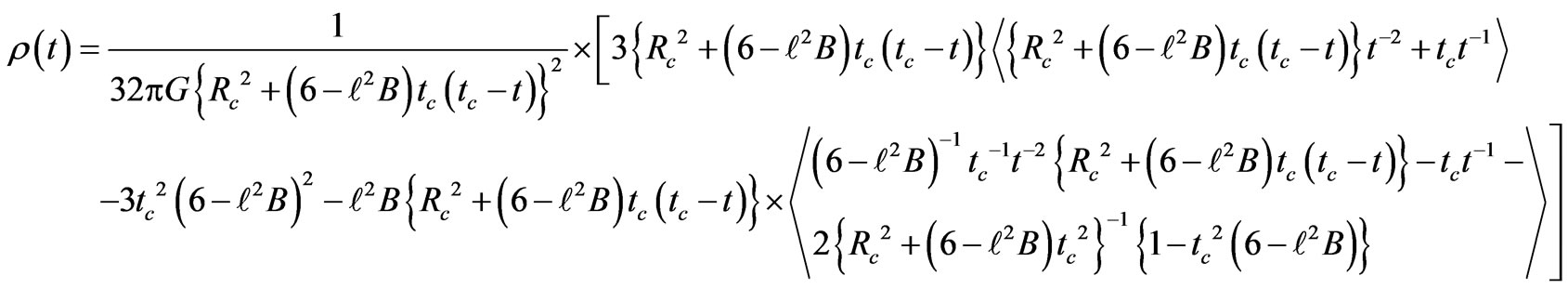
where  (80)
(80)
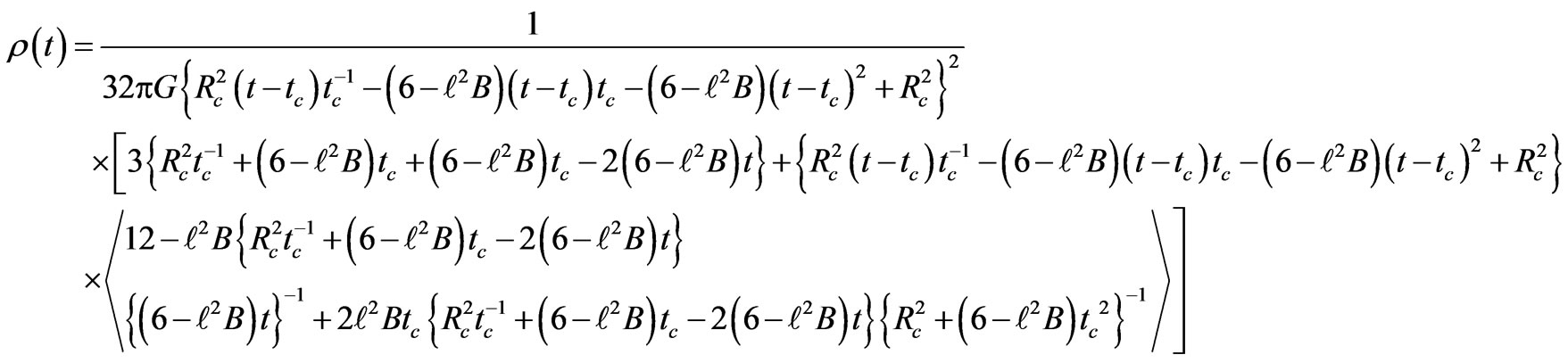
where
 (81)
(81)
Therefore, the discontinuity in the energy due to the phase transition occurring at  is given by
is given by
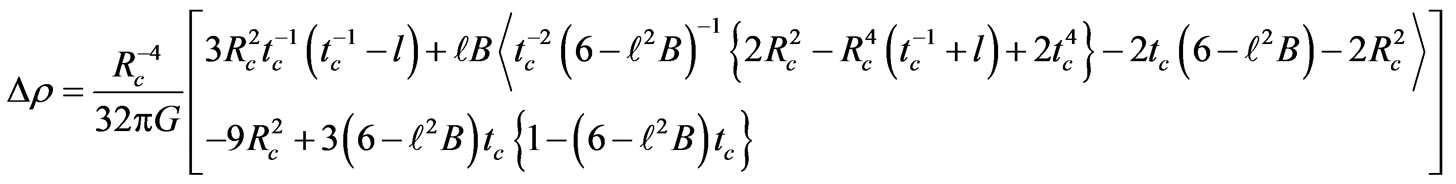 (82)
(82)
3. Conclusions
The models we obtain here are interesting as they ultimately evolve to the standard big bang models in the present era though their early scenarios are altogether different. Here solutions are obtained for spatially homogeneous and isotropic perfect fluid cosmological model in the presence of zero-mass scalar field which is one of the most acceptable models of the present universe. A unified description of early evolution of the universe is studied for two different periods where the gravitational constant is allowed to depend on cosmic time t. The models are expanding ones in each phase of evolution, and the solutions obtained in each phase are identically satisfied.
In case II (b)* we see that the phase transition occurs in the expanding phase of evolution (before reaching the maximum radius) at  when there is a sudden rise in the rate of expansion. And the subsequent evolution is affected by the scalar field. The larger the value of
when there is a sudden rise in the rate of expansion. And the subsequent evolution is affected by the scalar field. The larger the value of 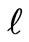 or in other words greater the strength of the scalar field the longer it will take for the universe to reach its maximum radius; and in this way the final collapse will be prolonged.
or in other words greater the strength of the scalar field the longer it will take for the universe to reach its maximum radius; and in this way the final collapse will be prolonged.
In Case II (b)** the model for

with k = l is an interesting one where the evolution for 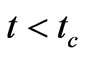 is akin to that of a standard Big Bang model with flat special sections. At
is akin to that of a standard Big Bang model with flat special sections. At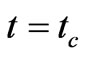 , the Hubble parameter suffers a sudden rise in its value which is due to a decrease in the hydrostatic pressure arising out of the presence of the scalar field. The subsequent evolution, therefore, starts with an increased rate of expansion. Here it is the presence of the scalar field which is instrumental in making the geometrically closed models ever expanding. Moreover relation (82) indicates that there is an instantaneous rise in the energy density after the phase transition in all ( k = 1,–1,0) big bang models, which may be interpreted as on account of generation of particles due to presence of scalar field.
, the Hubble parameter suffers a sudden rise in its value which is due to a decrease in the hydrostatic pressure arising out of the presence of the scalar field. The subsequent evolution, therefore, starts with an increased rate of expansion. Here it is the presence of the scalar field which is instrumental in making the geometrically closed models ever expanding. Moreover relation (82) indicates that there is an instantaneous rise in the energy density after the phase transition in all ( k = 1,–1,0) big bang models, which may be interpreted as on account of generation of particles due to presence of scalar field.
In case II (b) where a radiation-dominated phase is considered we see that both R and H are increasing functions of time thus showing that our universe is an expanding one. And also G is seen to be continuously increasing in this radiation-dominated phase.
Here the scalar field is found to exist only for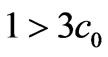 . Moreover the condition
. Moreover the condition  implies that the deceleration parameter q is greater than 2. Also in this case the pressure and energy density are found to be decreasing functions of time which shows that the evolving universe comes out to be one of the realistic models.
implies that the deceleration parameter q is greater than 2. Also in this case the pressure and energy density are found to be decreasing functions of time which shows that the evolving universe comes out to be one of the realistic models.
REFERENCES
- P. S. Wesson, “Gravity, Particles & Astrophysics,” D. Reidel, Dordrecht, 1980.
- P. A. M. Dirac, “A New Basis for Cosmology,” Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, Vol. 165, No. 921, pp. 199- 208.
- J. C. Carvalho, “Unified Description of the Early Universe,” International Journal of Theoretical Physics, Vol. 35, No. 9, 1996, pp. 2019-2028. doi:10.1007/BF02302426
- M. Israclit and N. Rosen, “A Singularity-Free Cosmological Model in General Relativity,” Astrophysical Journal, Vol. 342, 1989, pp. 627-632. doi:10.1086/167622
- D. Kalligas, P. Wesson and C. W. F. Everitt, “Flat FRW Models with Variable G and L,” General Relativity and Gravitation, Vol. 24, No. 4, 1992, pp. 351-357. doi:10.1007/BF00760411
- A. M. M. Abdel Rahman, “A Critical Density Cosmological Model with Varying Gravitational and Cosmological ‘Constants’,” General Relativity and Gravitation, Vol. 22, No. 6, 1990, pp. 655-657. doi:10.1007/BF00755985
- M. S. Berman, “Cosmological Models with a Variable Cosmological Term,” Physical Review D, Vol. 43, No. 4, 1991, pp. 1075-1078. doi:10.1103/PhysRevD.43.1075
- A. Beesham, “Variable-G Cosmology and Creation,” International Journal of Theoretical Physics, Vol. 25, No. 12, 1986, pp. 1295-1298. doi:10.1007/BF00670415
- L. S. Levit, “The Gravitational Constant at Time Zero,” Lettere Al Nuovo Cimento, Vol. 29, No. 1, 1980, pp. 23- 24. doi:10.1007/BF02745337
- R. F. Sistero, “Cosmology with G and L Coupling Scalars,” General Relativity and Gravitation, Vol. 23, No. 11, 1991, pp. 1265-1278. doi:10.1007/BF00756848
- K. Freese, F. C. Adams, J. A. Frieman and E. Mottola, “Cosmology with Decaying Vaccum Energy,” Nuclear Physics B, Vol. 287, 1987, pp. 797-814. doi:10.1016/0550-3213(87)90129-5
- C. P. Singh, “Bulk Viscous Cosmology in Early Universe,” Pramana, Vol. 71, No. 1, 2008, pp. 33-48. doi:10.1007/s12043-008-0139-4
- G. S. Khadekar, et al. “Early Viscous Universe with Variable Cosmological and Gravitational Constants in Higher Dimensional Space Time,” Physics and Astronomy, Vol. 47, No. 11, 2008, pp. 3057-3074. doi:10.1007/s10773-008-9741-y
- R. H. Brandenberger, “Cosmology of the Very Early Universe, 8 March 2010. arxiv: 1003. 1745VI [hep-th].
- C. G. Bohmer, K. Bolejko, A. Krasi´nski, C. Hellaby, M.-N. Célérier, “Structures in the Universe by Exact Methods,” Cambridge University Press, 2009, p. 256, GBP80.00, USD124.00, ISBN-13: 9780521769143 General Relativity and Gravitation, Vol. 43, No. 3, 2011, pp. 923-924. doi:10.1007/s10714-010-1126-x

