Applied Mathematics
Vol.07 No.15(2016), Article ID:70630,17 pages
10.4236/am.2016.715147
Rothe’s Fixed Point Theorem and the Controllability of the Benjamin-Bona-Mahony Equation with Impulses and Delay
Hugo Leiva1, Jose L. Sanchez2
1Department of Mathematics, Louisiana State University, Baton Rouge, USA
2Departamento de Matemática, Universidad de Los Andes, Caracas, Venezuela

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: May 7, 2016; Accepted: September 13, 2016; Published: September 16, 2016
ABSTRACT
For many control systems in real life, impulses and delays are intrinsic phenomena that do not modify their controllability. So we conjecture that under certain conditions the abrupt changes and delays as perturbations of a system do not destroy its controllability. There are many practical examples of impulsive control systems with delays, such as a chemical reactor system, a financial system with two state variables, the amount of money in a market and the savings rate of a central bank, and the growth of a population diffusing throughout its habitat modeled by a reaction-diffusion equation. In this paper we apply the Rothe’s Fixed Point Theorem to prove the interior approximate controllability of the following Benjamin-Bona-Mahony (BBM) type equation with impulses and delay
 where
where 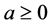 and
and 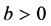 are constants,
are constants,  is a domain in
is a domain in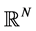 ,
, 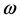 is an open non- empty subset of
is an open non- empty subset of ,
, 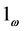 denotes the characteristic function of the set
denotes the characteristic function of the set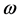 , the distributed control
, the distributed control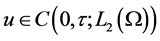 ,
, 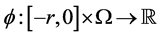 are continuous functions and the nonlinear functions
are continuous functions and the nonlinear functions  are smooth enough functions satisfying some additional conditions.
are smooth enough functions satisfying some additional conditions.
Keywords:
Interior Approximate Controllability, Benjamin-Bona-Mahony Equation with Impulses and Delay, Strongly Continuous Semigroup, Rothe’s Fixed Point Theorem

1. Introduction
For many control systems in real life, impulses and delays are intrinsic phenomena that do not modify their controllability. So we conjecture that under certain conditions the abrupt changes and delays as perturbations of a system do not destroy its controllability. There are many practical examples of impulsive control systems with delays, such as a chemical reactor system, a financial system with two state variables, the amount of money in a market and the savings rate of a central bank, and the growth of a population diffusing throughout its habitat modeled by a reaction-diffusion equation. One may easily visualize situations in these examples where abrupt changes such as harvesting, disasters and instantaneous stocking may occur. These problems can be modeled by impulsive differential equations with delays, and one can find information about impulsive differential equations in Lakshmikantham [1] and Samoilenko and Perestyuk [2] .
The controllability of impulsive evolution equations has been studied recently by several authors, but most of them study the exact controllability only. For example, D. N. Chalishajar [3] studied the exact controllability of impulsive partial neutral functional differential equations with infinite delay and S. Selvi and M. Mallika Arjunan [4] studied the exact controllability for impulsive differential systems with finite delay. For approximate controllability of impulsive semilinear evolution equation, Lizhen Chen and Gang Li [5] studied the approximate controllability of impulsive differential equations with nonlocal conditions, using measure of noncompactness and Monch Fixed Point Theorem, and assuming that the nonlinear term 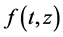 does not depend on the control variable. Recently, in [6] - [10] , the approximate controllability of semilinear evolution equations with impulses has been studied by applying Rothe’s Fixed Point Theorem, showing that the influence of impulses do not destroy the controllability of some known systems like the heat equation, the wave equation, the strongly damped wave equation. More recently, in [11] the approximate controllability of the heat equation with impulses and delay has been studied.
does not depend on the control variable. Recently, in [6] - [10] , the approximate controllability of semilinear evolution equations with impulses has been studied by applying Rothe’s Fixed Point Theorem, showing that the influence of impulses do not destroy the controllability of some known systems like the heat equation, the wave equation, the strongly damped wave equation. More recently, in [11] the approximate controllability of the heat equation with impulses and delay has been studied.
The approximate controllability of the linear part of the Benjamin-Bona-Mahony (BBM) equation was proved in [12] . This result was used to study the controllability of the nonlinear BBM equations in [13] , which could serve as a basis for studying the BBM equation under the influence of impulses and delays
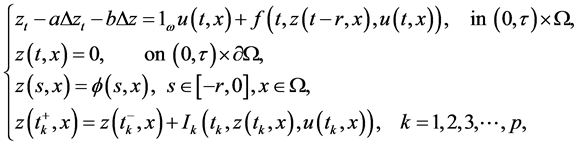 (1)
(1)
where  and
and 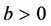 are constants,
are constants, 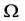 is a domain in
is a domain in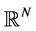 ,
, 











and
One natural space to work evolution equations with delay and impulses is the Banach space
where 

with
We shall denote by C the space of continuous functions:
endowed with the norm
Definition 1.1. (Approximate Controllability) The system (1) is said to be approximately controllable on 





where
As a consequence of this result we obtain the interior approximate controllability of the semilinear heat equation by putting 

We also study the approximate controllability of the corresponding linear system

by applying the classical Unique Continuation Principle for Elliptic Equations (see [14] ) and the following lemma.
Lemma 1.1. (see Lemma 3.14 from [15] , p. 62) Let 


if and only if
The approximate controllability of the system (1) follows from the approximate controllability of (4), the compactness of the semigroup generated by the associated linear operator, the conditions (2) and (3) satisfied by the nonlinear term 
Proposition 1.1. Let 




Theorem 1.1. (Rothe’s Fixed Theorem, [16] - [18] ) Let E be a Banach space and 

a) 
b) 


Then there is a point 
2. Abstract Formulation of the Problem
In this section we choose a Hilbert space where system (1) can be written as an abstract differential equation with impulses and delay; to this end, we consider the following notations:
Let 


The operator A has the following very well known properties (see N. I. Akhiezer and I. M. Glazman [19] ): the spectrum of A consists of eigenvalues

each one with finite multiplicity 
a) There exists a complete orthonormal set 
b) For all 

where 

So, 

c) 


Consequently, the system (1) can be written as abstract differential equations with impulses and delay in Z:

where








On the other hand, from conditions (2) and (3) we get the following estimates.
Proposition 2.1. Under the conditions (2)-(3) the functions





Since 



is invertible with bounded inverse

Therefore, the systems (11) and its linear part can be written as follows, for


Moreover, 



Therefore, if we put 



and the functions F defined above satisfy:

Now, we formulate two simple propositions.
Proposition 2.2. ( [12] ) The operators 



Moreover, the following estimate holds

where

Observe that, due to the above notation, systems (20)-(21) can be written as follows


where
3. Preliminaries on Controllability of the Linear Equation
In this section we prove the interior controllability of the linear system (28). To this end, notice that for an arbitrary 


admits only one mild solution given by

Definition 3.1. For the system (29) we define the following concept: The controllability map (for


whose adjoint operator 

The following lemma holds in general for a linear bounded operator 
Lemma 3.1. (see [15] [20] [21] and [22] ) The Equation (28) is approximately controllable on 
a)
b)
c)

d)
e)
f) For all 

So, 

Remark 3.1. The Lemma 3.1 implies that the family of linear operators 


is an approximate inverse for the right of the operator G in the sense that

Proposition 3.4. (see [21] ) If

Theorem 3.1. The system (28) is approximately controllable on




and the error of this approximation 
Proof. It is enough to show that the restriction 




whose adjoint operator 
Since B is given by the formula
and 


Suppose that
Then we have that
where

Hence, following the proof of Lemma 1.1, we obtain that
Now, putting
Then, from the classical Unique Continuation Principle for Elliptic Equations (see [14] ), it follows that
On the other hand, 


Therefore, 



Lemma 3.2. Let S be any dense subspace of


where 
Proof (Þ) Suppose 





Therefore, 


(Ü) This side is trivial. W
Remark 3.2 According to the previous Lemma, if the system is approximately controllable, it is approximately controllable with control functions in the following dense spaces of
Moreover, the operators G, 



and 

Also, the Controllability Grammian operator is still the same

Finally, the operators 


is an approximate inverse for the right of the operator G in the sense that

4. Main Result
In this section we prove the main result of this paper, the interior controllability of the semilinear BBM Equation with impulses and delay given by (1), which is equivalent to prove the approximate controllability of the system (27). To this end, observe that for all 


admits only one mild solution given by the formula

Now, we are ready to present and prove the main result of this paper, which is the interior approximate controllability of the Benjamin-Bona-Mahony (1) with impulses and delay.
Define the operator 
where

and

with 

Theorem 4.1. The nonlinear system (1) is approximately controllable on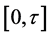




and the error of this approximation 
where

Proof. We shall prove this Theorem by claims. Before, we note that 

Claim 1. The operator 
and
define above are continuous. The continuity of 


On the other hand,
Therefore,
where 

The continuity of the operator 


Claim 2. The operator 


Therefore, 
Now, consider the following estimate:
Without lose of generality we assume that
and
Since 


Consequently, if we take a sequence 





Consider the sequence 




Continuing this process for the intervals






Claim 3.
where 

where
and
Therefore,
where 
Hence
and

Claim 4. The operator 


Hence, if we denote by 







Claim 5. The sequence 


On the other hand, from (48) we know for all 
Particularly, we have the following situation:
Now, applying Cantor’s diagonalization process, we obtain that
and from (49) we have that
which is evidently a contradiction. Then, the claim is true and there exists 
Therefore, without loss of generality, we can assume that the sequence 

Then,
Hence,
To conclude the proof of this Theorem, it enough to prove that
From Lemma 3.2.d) we get that
Now, from Proposition 3.1, we get that
Therefore, since 
Consequently,
Then,
Therefore,
and the proof of the theorem is completed. W
As a consequence of the foregoing theorem we can prove the following characterization:
Theorem 4.2. The Impulsive Semilinear System (1) is approximately controllable if for all states 




5. Conclusions
Our technique can be applied to those control systems whose linear parts generate a compact semigroup and are under the influence of impulses and delays, as well as the following examples which represent research problems.
Problem 1. It appears that our technique can also be applied to prove the interior controllability of the strongly damped wave equation with impulses and delay
in the space










Problem 2. Our technique may also be applied to a system given by partial differential equations modeling the structural damped vibrations of a string or a beam with impulses and delay
Here 








Acknowledgements
We thank the Editor and the referee for their comments. This research was funded by the BCV. This support is greatly appreciated.
Competing Interests
The authors declare that there is not competing of interests.
Cite this paper
Leiva, H. and Sanchez, J.L. (2016) Rothe’s Fixed Point Theorem and the Controllability of the Benjamin-Bona-Mahony Equation with Impulses and Delay. Applied Mathematics, 7, 1748- 1764. http://dx.doi.org/10.4236/am.2016.715147
References
- 1. Lakshmikantham, V., Bainov, D.D. and Simeonov, P.S. (1989) Theory of Impulsive Differential Equations. World Scientific, Singapore.
http://dx.doi.org/10.1142/0906 - 2. Samoilenko, A.M. and Perestyuk, N.A. (1995) Impulsive Differential Equations. World Scientific, Singapore.
http://dx.doi.org/10.1142/2892 - 3. Chalishajar, D.N. (2011) Controllability of Impulsive Partial Neutral Functional Differential Equation with Infinite Delay. International Journal of Mathematical Analysis, 5, 369-380.
- 4. Selvi, S. and Mallika Arjunan, M. (2012) Controllability Results for Impulsive Differential Systems with Finite Delay. The Journal of Nonlinear Science and Applications, 5, 206-219.
- 5. Chen, L.Z. and Li, G. (2010) Approximate Controllability of Impulsive Differential Equations with Nonlocal Conditions. International Journal of Nonlinear Science, 10, 438-446.
- 6. Carrasco, A., Leiva, H., Sanchez, J.L. and Tineo Moya, A. (2014) Approximate Controllability of the Semilinear Impulsive Beam Equation with Impulses. Transaction on IoT and Cloud Computing, 2, 70-88.
- 7. Leiva, H. (2014) Rothe’s Fixed Point Theorem and Controllability of Semilinear Nonautonomous Systems. System and Control Letters, 67, 14-18.
http://dx.doi.org/10.1016/j.sysconle.2014.01.008 - 8. Leiva, H. (2014) Controllability of Semilinear Impulsive Nonautonomous Systems. International Journal of Control, 88, 582-592.
http://dx.doi.org/10.1080/00207179.2014.966759 - 9. Leiva, H. and Merentes, N. (2015) Approximate Controllability of the Impulsive Semilinear Heat Equation. Journal of Mathematics and Applications, 38, 85-104.
- 10. Leiva, H. (2015) Approximate Controllability of Semilinear Impulsive Evolution Equations. Abstract and Applied Analysis, 2015, Article ID: 797439.
- 11. Leiva, H. (2015) Approximate Controllability of Semilinear Heat Equation with Impulses and Delay on the State. Nonautonomous Dynamical Systems, 2, 52-62.
- 12. Leiva, H., Merentes, N. and Sanchez, J. (2010) Interior Controllability of the Benjamin-Bona-Mahony Equation. Journal of Mathematics and Applications, 33, 51-59.
- 13. Leiva, H., Merentes, N. and Sanchez, J. (2012) Interior Controllability of the Semilinear Benjamin-Bona-Mahony Equation. Journal of Mathematics and Applications, 35, 97-109.
- 14. Protter, M.H. (1960) Unique Continuation for Elliptic Equations. Transaction of the American Mathematical Society, 95, No 1.
http://dx.doi.org/10.1090/S0002-9947-1960-0113030-3 - 15. Curtain, R.F. and Pritchard, A.J. (1978) Infinite Dimensional Linear Systems. Lecture Notes in Control and Information Sciences, Springer Verlag, Berlin.
- 16. Banas, J. and Goebel, K. (1980) Measures of Noncompactness in Banach Spaces. Lecture Notes in Pure and Applied Mathematics, Marcel Dekker, Inc., New York.
- 17. Isac, G. (2004) On Rothe’s Fixed Point Theorem in General Topological Vector Space. An. St. Univ. Ovidius Constanta, 12, 127-134.
- 18. Smart, J.D.R. (1974) Fixed Point Theorems. Cambridge University Press.
- 19. Akhiezer, N.I. and Glazman, I.M. (1993) Theory of Linear Operators in Hilbert Space. Dover Publications.
- 20. Curtain, R.F. and Zwart, H.J. (1995) An Introduction to Infinite Dimensional Linear Systems Theory. Text in Applied Mathematics, Springer Verlag, New York.
http://dx.doi.org/10.1007/978-1-4612-4224-6 - 21. Leiva, H., Merentes, N. and Sanchez, J. (2013) A Characterization of Semilinear Dense Range Operators and Applications. Abstract and Applied Analysis, 2013, Article ID: 729093.
- 22. Bashirov, A.E., Mahmudov, N., Semi, N. and Etikan, H. (2007) Partial Controllability Concepts. International Journal of Control, 80, 1-7.
http://dx.doi.org/10.1080/00207170600885489












































































