Applied Mathematics
Vol.07 No.07(2016), Article ID:66032,12 pages
10.4236/am.2016.77059
Thermal Diffusion Effect on MHD Heat and Mass Transfer Flow past a Semi Infinite Moving Vertical Porous Plate with Heat Generation and Chemical Reaction
Gurivireddy P.1, Raju M. C.2*, Mamatha B.3, Varma S. V. K. 3
1Department of Mathematics, S.B.V.R, Degree College, Badvel, India
2Department of Humanities and Sciences, Annamacharya Institute of Technology and Sciences (Autonomous), Rajampet, India
3Department of Mathematics, S. V. University, Tirupati, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 February 2016; accepted 25 April 2016; published 28 April 2016
ABSTRACT
The objective of present work is to study the thermo diffusion effect on an unsteady simultaneous convective heat and mass transfer flow of an incompressible, electrically conducting, heat generating/absorbing fluid along a semi-infinite moving porous plate embedded in a porous medium with the presence of pressure gradient, thermal radiation field and chemical reaction. It is assumed that the permeable plate is embedded in a uniform porous medium and moves with a constant velocity in the flow direction in the presence of a transverse magnetic field. It is also assumed that the free stream consists of a mean velocity, temperature and concentration over which are super imposed an exponentially varying with time. The equations of continuity, momentum, energy and diffusion, which govern the flow field, are solved by using a regular perturbation method. The behavior of the velocity, temperature, concentration, Skin-friction, rate of heat transfer and rate of mass transfer has been discussed for variations in the physical parameters. An increase in both Pr and R results a decrease in thermal boundary layer thick-ness. However, concentration decreases as Kr, Sc in-crease but it increases with an increase in both So and δ.
Keywords:
Heat Generation/Absorption, Chemical Reaction, MHD, Thermal Radiation, Thermal Diffusion, Heat and Mass Transfer, Semi-Infinite Vertical Plate

1. Introduction
The study of magneto hydrodynamic flows through porous media is of considerable interest because of its abundant applications in several branches of science and technology; such as in astrophysical, geo-physical problem and in developing magnetic generator for obtaining electrical energy at minimum cost. The theory developed by viscous flow through porous media is useful in analyzing the influence of temperature and pressure on the flow of soil water. The unsteady free convection flows over semi-infinite vertical plate was studied by Takhar et al. [1] . Thakar and Ram [2] also studies the MHD free porous convection heat transfer of water at 400C through a porous medium. Raju and Varma [3] considered the unsteady MHD free convection oscillatory Couette flow through a porous medium with periodic wall temperature. In the context of space technology in process involving high temperatures, the effects of radiation are of vital importance. Recent developments in hypersonic flights, missile, rocket combustion chambers, power plants for inter planetary flight and gas cooled nuclear reactors, have focused attention on thermal radiation as a mode of energy transfer, and emphasize the need for improved understanding of radiative transfer in these process. Several authors (Raju et al., [4] ; Nath et al., [5] ; Raptis and Perdikis, [6] ; Bakier, [7] ; Kim, [8] ; Chamkha and Khaled [9] ) have studied thermal radiating MHD boundary layer flows with applications in astrophysical fluid dynamics. Combined the heat and mass transfer problems with chemical reaction are of importance in many processors and have there-fore received a considerable amount of attention in recent years. Das et al. [10] have studied the effect of homogeneous first order chemical reaction on the flow past an impulsively started infinite vertical plate with uniform heat flux. Unsteady MHD free convection and chemically reactive flow past an infinite vertical porous plate was studied by Raju et al. [11] . Chamka [12] studied the MHD flow past a uniformly stretched vertical permeable surface in the presence of heat generation/absorption. As per, Mahdy and Ah-med [13] , the Soret effect, for instance, has been utilized for isotope separation, and in mixture between gases with very light molecular weight (H2, He). Raju et al. [14] analyzed the Soret effects due to natural convection between heated inclined plates with magnetic field. Recently Ablel-Rahman [15] studied the thermal diffusion effect on MHD combined free forced convection and mass transfer flow of a viscous fluid through a porous medium with heat generation. Thermo diffusion and chemical effects with simultaneous thermal and mass diffusion in MHD mixed convection flow with Ohmic heating was considered by Reddy, A. et al. [16] . Recently Sarma et al. [17] studied MHD free convection and mass transfer flow past an accelerated vertical plate with chemical reaction in presence of radiation. Ahmed and Batin [18] considered magneto-hydrodynamic heat and mass transfer flow with induced magnetic field and viscous dissipative effects. Mutuku-Njane and Makinde [19] investigated on hydromagnetic boundary layer flow of nanofluids over a permeable moving surface with Newtonian heating.
Motivated by the above studies, in this paper we have considered thermo diffusion effect on an unsteady simultaneous convective heat and mass transfer flow of an incompressible, electrically conducting, heat generating/absorbing fluid along a semi-infinite moving porous plate embedded in a porous medium with the presence of pressure gradient, thermal radiation field and chemical reaction. The novelty of this study is the consideration of a double diffusion fluid (mass diffusion and as we as thermal diffusion) along with chemical reaction and heat source of a radiating fluid past or through a porous plate in a conducting filed. In spite of that many authors contributed similar works, still there are many interesting aspects to be concentrated. Hence authors are interested to carry on this investigation.
2. Mathematical Analysis
Consider a two-dimensional unsteady flow of a laminar incompressible electrically conducting and heat generating/absorbing fluid with mass transfer, past a semi-infinite vertical porous plate embedded in a porous medium in the presence of thermal radiation, chemical reaction and thermal diffusion. A uniform magnetic field is applied perpendicular to the plate. There is no applied voltage which implies the absence of the electric field. The transversely applied magnetic field and magnetic Reynolds number are assumed to be small and hence the induced magnetic field is negligible. Since the plate is semi-infinite in length all the flow variables are functions of y and t only. Under the above conditions and the usual Boussinesq’s approximation the governing equations are given as:
Continuity equation:
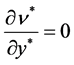 (1)
(1)
Momentum equation:
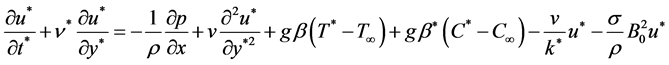 (2)
(2)
Energy equation:
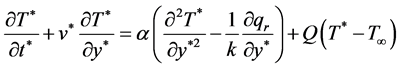 (3)
(3)
Species diffusion equation:
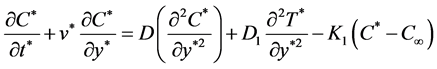 (4)
(4)
By using the Rosseland approximation the radiative heat flux in y direction is given by
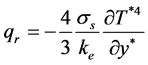 (5)
(5)
where σs and ke are the Stefan-Boltzmann constant and the mean absorption coefficient, respectively. It should be noted that by using the Rosseland approximation we limit our analysis to optically thick fluids. It is assumed that the temperature differences are small, then Equation (5) can be linearized by expanding T*4 into Taylor series about T∞, and neglecting higher order terms to give:
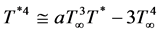 (Raju et al. (2012)) (6)
(Raju et al. (2012)) (6)
The heating due to viscous dissipation is neglected for small velocities in energy conservation Equation (3) and Boussinesq approximation is used to describe buoyancy force in Equation (2). It is assumed that the free stream velocity, the suction velocity, the plate temperature and the plate concentration follow an exponentially increasing or decreasing small perturbation law.
Under these assumptions, the appropriate boundary conditions for the velocity, temperature and concentration fields are
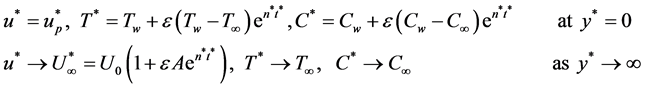 (7)
(7)
From the continuity equation, it is clear that the suction velocity normal to the plate is a function of time only and we shall take it in the form
 (8)
(8)
where A is a real positive constant, ε and εA are small less than unity, and V0 is scale of suction velocity which is a non-zero positive constant. Outside the boundary layer, Equation (2) gives
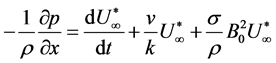 (9)
(9)
Now introduce non-dimensional parameters as follows
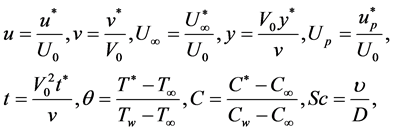
 (10)
(10)
After substituting boundary conditions and dimensionless parameters the governing Equations (2)-(5) reduce to
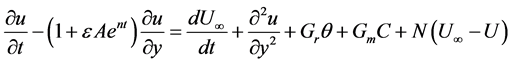 (11)
(11)
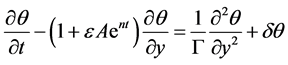 (12)
(12)
 (13)
(13)
where  and
and
The boundary conditions (7) are given by the following non-dimensional form

3. Solution of the Problem
In order to reduce the above system of partial differential equations to a system of ordinary differential equations in dimensionless form, for



Substituting these Equations (15)-(17) into Equations (11)-(13) and equating the harmonic and non-harmonic terms, also neglecting the coefficient of O(e2), we get the following pairs of equations.






Here primes denote differentiation with respect to y.
The corresponding boundary conditions are

The solutions of Equations (18)-(23) with satisfying boundary conditions (24) are given by









Given the velocity field in the boundary layer, we can now calculate the skin friction at the wall as

We calculate the heat transfer coefficient in terms of Nusselt number as follows

Similarly the mass transfer coefficient in terms of Sherwood number, as follows

4. Results and Discussion
In order to assess the accuracy of the numerical results, we have compared our results with accepted data sets for the velocity, temperature and concentration profiles for a stationary vertical porous plate corresponding to the case computed by Kim (2000). i.e., in the absence of the diffusion effects we observed that the effects of all parameters on velocity and temperature profiles are in good agreement with the comparison of Kim (2000).
Figure 1 illustrates the behavior of the velocity for different values of chemical reaction parameter Kr. It is seen that the velocity decreases with increasing chemical reaction parameter Kr. For large value of chemical reaction parameter effect on velocity is negligible as y increases. Figure 2 shows the velocity profiles for different values of magnetic parameter M and Grashof number Gr.
It is noticed that the velocity decreases slightly with the increase of magnetic parameter M, also observed that the velocity increases with thermal Grashoff number Gr. But when the value of Gr increases the effect of magnetic parameter on velocity has high impact. The effect of the porosity parameter K on the velocity profiles has been shown in Figure 3. It is observed that the velocity increases as porosity parameter increases along the boundary layer. For different values of Prandtl number Pr and radiation parameter R, the temperature profiles are plotted in Figure 4. The results show that an increase of both Prandtl number Pr and radiation parameter R results a decrease in the thermal boundary layer. Figure 5 displays the effects of heat generation and exponential index n on temperature profiles across the boundary layer. It is found that an increase in the value of n leads to an increase in the temperature distribution across the boundary layer. Also it is observed that the effect of increasing values of δ results in a decreasing temperature distribution. Figure 6 depicts the effect of Schmidt number Sc and chemical reaction parameter Kr on concentration profiles. The concentration decreases as the chemical reaction parameter Kr increases. Also the figure shows that an increase in Sc results in a decrease in the concentration distribution, because the smaller values of Sc are equivalent to increasing the chemical molecular diffusivity. The influence of Soret effect So and heat generation parameter δ on the concentration profiles are shown in Figure 7.
From this figure we see that the concentration increases with the increase of both Soret number So and heat generation parameter. We have also shown some Tables 1-3 of the skin-friction, rate of heat transfer and rate of mass transfer by the effects of the Gr, Gm, K, M, Pr, Sc, R, Kr, δ and So. From these tables it is noticed that the
Figure 1. Effects of chemical reaction parameter on velocity.
Figure 2. Effects of magnetic parameter on velocity.
Figure 3. Effects of porosity parameter K on velocity.
Figure 4. Effects of Prandtl number Pr and radiation parameter R on temperature.
Figure 5. Effects of heat generation parameter δ and exponential index n on temperature.
Figure 6. Effects of Schmidt number Sc and chemical reaction parameter Kr on concentration.
Figure 7. Effects of So and δ on concentration.
Table 1. Effects of R, δ and Pr on skin-friction, Nusselt number and Sherwood number.
Table 2. Effects of So, Sc, Kr on skin-friction and rate of mass transfer.
Table 3. Effects of Gr, Gm, K and M on skin-friction.
skin-friction at the wall increases as Grashoff number Gr or modified Grashoff number Gm or Soret number So or heat generation/absorption parameter δ increases. And it decreases with increasing Prandtl number Pr or Schmidt number Sc or radiation parameter R or chemical reaction parameter Kr or permeability parameter K or magnetic parameter M. From the analytical results, it can be seen that the rate of heat transfer depends on radiation parameter R, Prandtl number Pr and heat generation/absorption parameter δ and the rate of mass transfer depends on chemical reaction parameter Kr, Schmidt number Sc and Soret number So and the Prandtl, radiation, and heat generation/absorption as well.
The mentioned tables reveal that as Schmidt number or chemical reaction parameter increases, the rate of mass transfer (Sh) increases but it decreases with the increase of Prandtl number Pr or Soret number So or radiation parameter R. Also we observe that the rate of heat transfer (Nu) increases with the increase of Prandtl number or radiation parameter but it decreases with increasing heat generation parameter.
5. Conclusion
We have considered thermo diffusion effect on an unsteady simultaneous convective heat and mass transfer flow of an incompressible, electrically conducting, heat generating/absorbing fluid along a semi-infinite moving porous plate embedded in a porous medium with the presence of pressure gradient, thermal radiation field and chemical reaction.
1) An increase in K leads to a raise in the velocity but a reverse effect is seen in the case of Kr and M.
2) An increase in both Pr and R results a decrease in thermal boundary layer thickness. However, concentration decreases as Kr, Sc increase but it increases with an increase in both So and δ.
3) The skin-friction at the wall increases as Gr and Gm or M or So or δ increases and it decreases with increase in Pr or Sc or R or Kr or K.
4) As Sc or Kr increase, the rate of mass transfer increases but it decreases with the increase in Pr or So or R. Also we observe that the rate of heat transfer increases with the increase of Pr or R but it decreases with decreasing δ.
5) This work can be extended for other non-Newtonian fluids such as viscoelastic fluid, Rivlin Ericksen fluid, micropolar fluid etc.,
Acknowledgements
Authors are very much thankful to the anonymous reviewers for giving the constructive suggestion which helped us in improving the quality of the manuscript.
Cite this paper
Gurivireddy P.,Raju M. C.,Mamatha B.,Varma S. V. K., (2016) Thermal Diffusion Effect on MHD Heat and Mass Transfer Flow past a Semi Infinite Moving Vertical Porous Plate with Heat Generation and Chemical Reaction. Applied Mathematics,07,638-649. doi: 10.4236/am.2016.77059
References
- 1. Takhar, H.S, Ganesan, P., Ekambavahar, K. and Soundalgekar, V.M. (1997) Transient Free Convection past a Semi-Infinite Vertical Plate with Variable Surface Temperature. International Journal of Numerical Methods for Heat & Fluid Flow, 7, 280-296.
http://dx.doi.org/10.1108/09615539710165804 - 2. Takhar, H.S. and Ram, P.C. (1994) Magneto Hydrodynamics Free Convection Flow of Water at 400C through a Porous Medium. International Communications in Heat and Mass Transfer, 21, 371-376.
http://dx.doi.org/10.1016/0735-1933(94)90005-1 - 3. Raju, M.C. and Varma, S.V.K. (2011) Unsteady MHD Free Convection Oscillatory Couette Flow through a Porous Medium with Periodic Wall Temperature. Journal on Future Engineering and Technology, 6, 7-12.
- 4. Raju, M.C., Varma S.V.K. and Ananda Reddy, N. (2012) Radiation and Mass Transfer Effects on a Free Convection flow Through a Porous Medium Bounded by a Vertical Surface. Journal of Future Engineering and Technology, 7, 7-12.
- 5. Nath, O., Ojha, S.N. and Takhar, H.S. (1991) A Study of Stellar Point Explosion in a Radiative MHD Medium. Astro physics and Space Sciences, 183, 135-145.
- 6. Raptis, A. and Perdikis, C. (1999) Radiation and Free Convection Flow past a Moving Plate. Applied Mechanics and Engineering, 14, 817-821.
- 7. Bakier, A.Y. (2001) Thermal Radiation Effect on Mixed Convection from Vertical Surfaces in Saturated Porous Media. Indian Journal of Pure and Applied Mathematics, 32, 1157-1163.
- 8. Kim, Y.J. (2000) Unsteady MHD Convective Heat Transfer past a Semi-Infinite Vertical Porous Plate with Variable Suction. International Journal of Engineering Science, 38, 833-845.
http://dx.doi.org/10.1016/S0020-7225(99)00063-4 - 9. Hamkha, A.J. and Khaled, A.R.A. (2001) Similarity Solutions for Hydro Magnetic Simultaneous Heat and Mass Transfer by Natural Convection from an Inclined Plate with Internal Heat Generation or Absorption. Heat and Mass Transfer, 37, 117-123.
http://dx.doi.org/10.1007/s002310000131 - 10. Das, U.N., Dekha, R.K. and Soundalgekar, V.M. (1994) Effects of Mass Transfer on Flow Past an Impulsively Started Infinite Vertical Plate with Constant Heat Flux and Chemical Reaction. Forschung in Ingenieurwsen, 60, 284-287.
http://dx.doi.org/10.1007/BF02601318 - 11. Raju, M.C., Varma, S.V.K. and Rao, R.R.K. (2013) Unsteady MHD Free Convection and Chemically Reactive Flow past an Infinite Vertical Porous Plate. I-Manager Journal of Future Engineering and Technology, 8, 35-40.
- 12. Chamkha, A.J. (2000) Thermal Radiation and Buoyancy Effects on Hydro Magnetic Flow over an Accelerating Permeable Surface with Heat Source or Sink. International Journal of Heat and Mass Transfer, 38, 1699-1712.
- 13. Mahdy, A. and Ahmed, S.E. (2015) Thermosolutal Marangoni Boundary Layer Magnetohydrodynamic Flow with the Soret and Dufour Effects past a Vertical Flat Plate. Engineering Science and Technology, an International Journal, 18, 24-31.
- 14. Raju, M.C., Varma, S.V.K., Reddy, P.V. and Saha, S. (2008) Soret Effects Due to Natural Convection between Heated Inclined Plates with Magnetic Field. Journal of Mechanical Engineering, ME39, 43-48.
- 15. Ablel-Rahman, G.M. (2008) Thermal Diffusion and MHD Effects on Combined Free Forced Convection and Mass Transfer Flow of a Viscous Fluid Flow through a Porous Medium with Heat Generation. Chemical Engineering and Technology, 31, 554-559.
http://dx.doi.org/10.1002/ceat.200700487 - 16. Reddy, N.A., Raju, M.C. and Varma, S.V.K. (2009) Thermo Diffusion and Chemical Effects with Simultaneous Thermal and Mass Diffusion in MHD Mixed Convection Flow with Ohmic Heating. Journal of Naval Architecture and Marine Engineering, 6, 84-93.
- 17. Sarma, D., Ahmed, N. and Deka, H. (2014) MHD Free Convection and Mass Transfer Flow past an Accelerated Vertical Plate with Chemical Reaction in Presence of Radiation. Latin American Applied Research, 44, 1-8.
- 18. Ahmed, S. and Batin, A. (2014) Magnetohydrodynamic Heat and Mass Transfer Flow with Induced Magnetic Field and Viscous Dissipative Effects. Latin American Applied Research, 44, 9-17.
- 19. Mutuku-Njane, W.N. and Makinde, O.D. (2014) On Hydromagnetic Boundary Layer Flow of Nanofluids over a Permeable Moving Surface with Newtonian Heating. Latin American Applied Research, 44, 57-62.
Nomenclature
Appendix
NOTES
*Corresponding author.











