Applied Mathematics
Vol.07 No.09(2016), Article ID:66807,27 pages
10.4236/am.2016.79078
Regular Elements of 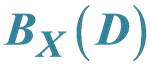 Defined by the Class
Defined by the Class 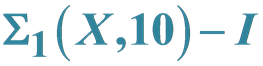
Yasha Diasamidze1, Nino Tsinaridze1, Neşet Aydn2, Ali Erdoğan3
1Shota Rustavelli University, Batumi, Georgia
2Çanakkale Onsekiz Mart University, Çanakkale, Turkey
3Hacettepe University, Ankara, Turkey

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 January 2016; accepted 24 May 2016; published 27 May 2016
ABSTRACT
In order to obtain some results in the theory of semigroups, the concept of regularity, introduced by J. V. Neumann for elements of rings, is useful. In this work, all regular elements of semigroup defined by semilattices of the class 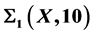 are studied. When X has finitely many elements, we have given the number of regular elements.
are studied. When X has finitely many elements, we have given the number of regular elements.
Keywords:
Semilattice, Semigroup, Binary Relation

1. Introduction
Let D be a nonempty set of subsets of a given set X, closed under union. Such a set D is called a complete X-semilattice of unions. For any map f from X to D, we define a binary relation.
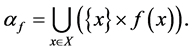
The set of all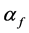 , denoted by
, denoted by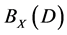 , is a subsemigroup of
, is a subsemigroup of 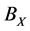 semigroup of all binary relations on X. (See [1] - [6] .)
semigroup of all binary relations on X. (See [1] - [6] .)
All notations, symbol and required definitions used in this work can be found in [7] . Recall the following results.
Lemma 1. [1] , Corollary 1.18.1. Let 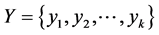 and
and 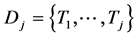 be two sets where
be two sets where 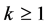 and
and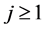 . Then the number
. Then the number 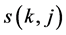 of all possible mappings from Y to subsets
of all possible mappings from Y to subsets 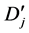 of
of 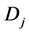 such that
such that 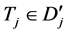 is given by
is given by![]() .
.
Theorem 1. [1] , Theorem 1.18.1. Let![]() . Let
. Let ![]() be nonempty sets. Then the number
be nonempty sets. Then the number
of mappings from X to ![]() such that
such that ![]() for some
for some ![]() is equal to
is equal to![]() .
.
2. Results
Let X be a nonempty set, D a X-semilattice of union with the conditions (see Figure 1);
![]() (1)
(1)
The class of X-semilattices where each element is isomorphic to D is denoted by![]() .
.
An element ![]() is called regular if
is called regular if ![]() for some
for some![]() . Our aim in this work is to identify all regular elements of
. Our aim in this work is to identify all regular elements of ![]() where D is given above.
where D is given above.
Definition 1. The complete X-semilattice of unions is called an XI-semilattice of unions if ![]()
and ![]() for any nonempty Z in D. Here
for any nonempty Z in D. Here ![]() is an exact lower bound of
is an exact lower bound of ![]() in D where
in D where
![]()
The following Lemma is well known (see [7] , Lemma 3).
Lemma 2. All semilattices in the form of the diagrams in Figure 2 are XI-semilattices.
![]()
Figure 1. Diagram of semilattice of unions D.
![]()
Figure 2. Diagram of all XI-subsemilattices of D.
Definition 2. Let ![]() and
and ![]() be two X-semilattices of unions. A one to one map from
be two X-semilattices of unions. A one to one map from ![]() to
to ![]() is said to be a complete isomorphism if
is said to be a complete isomorphism if
![]()
for ![]()
Definition 3. [1] , Definition 6.3.3. Let![]() . We say that a complete isomorphism
. We say that a complete isomorphism ![]() is a complete a-isomorphism if
is a complete a-isomorphism if
a) ![]()
b) ![]() for
for ![]() and
and ![]() for any
for any![]() .
.
The following subsemilattices are all XI-semilattices of the X-semilattices of unions D.
a)![]() , where
, where ![]() (see diagram 1 of the Figure 3);
(see diagram 1 of the Figure 3);
b) ![]() where
where ![]() and
and ![]() (see diagram 2 of the Figure 3);
(see diagram 2 of the Figure 3);
c) ![]() where
where ![]() and
and ![]() (see diagram 3 of the Figure 3);
(see diagram 3 of the Figure 3);
d) ![]() where
where ![]() and
and ![]() (see diagram 4 of the Figure 3);
(see diagram 4 of the Figure 3);
e) ![]() where
where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , (see diagram 5 of the Figure 3);
, (see diagram 5 of the Figure 3);
f) ![]() where
where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
(see diagram 6 of the Figure 3);
g)![]() , where
, where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (see diagram 7 of the Figure 3);
(see diagram 7 of the Figure 3);
h)![]() , where
, where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (see diagram 8 of the Figure 3);
(see diagram 8 of the Figure 3);
For each ![]() we set
we set ![]()
One can see that
![]()
Assume that ![]() and denote by the symbol
and denote by the symbol ![]() the set of all regular elements a of the semigroup
the set of all regular elements a of the semigroup
![]()
Figure 3. Diagram of all subsemilattices isomorphic to subsemilattices in Figure 2.
![]() , for which the semilattices
, for which the semilattices ![]() and
and ![]() are mutually a-isomorphic and
are mutually a-isomorphic and ![]() and
and
![]()
(see [1] , Definition 6.3.5).
The following results have the key role in this study.
Theorem 2. Let ![]() be the set of all regular elements of the semigroup
be the set of all regular elements of the semigroup![]() . Then the following state- ments are true:
. Then the following state- ments are true:
a) ![]() for any
for any ![]() and
and![]() ;
;
b)![]() ;
;
c) if X is a finite set, then ![]() (see [1] , Theorem 6.3.6).
(see [1] , Theorem 6.3.6).
Lemma 3. Let ![]() be isomorphism between
be isomorphism between ![]() and
and ![]() semilattices,
semilattices, ![]() ,
, ![]() and
and![]() . If X is a finite set and
. If X is a finite set and ![]()
![]() , then the following equalities are true:
, then the following equalities are true:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
f) ![]()
g) ![]()
h) ![]()
Proof. The propositions a), b), c) and d) immediately follow from ( [1] , Theorem 6.3.5 and Theorem 13.1.2), while the equalities e), f), g) and h) follow from ( [1] , Theorem 6.3.5, Corolaries 13.3.4-5-6 and 13.7.3). □
3. Regular Elements of the Complete Semigroups of Binary Relations of the Class ![]() , When
, When ![]() and
and ![]()
Theorem 3. Let ![]() and
and![]() . Then a binary relation a
. Then a binary relation a
of the semigroup ![]() whose quasinormal representation has the form
whose quasinormal representation has the form ![]() will be a
will be a
regular element of this semigroup iff there exist a complete a-isomorphism ![]() of the semilattice
of the semilattice ![]() on some subsemilattice
on some subsemilattice ![]() of the semilattice D which satisfies at least one of the following conditions:
of the semilattice D which satisfies at least one of the following conditions:
a)![]() , for some
, for some![]() ;
;
b)![]() , for some
, for some![]() ,
, ![]() and
and ![]() which satisfies the condi- tions:
which satisfies the condi- tions:![]() ,
,![]() ;
;
c)![]() , for some
, for some![]() ,
, ![]() , and
, and ![]() which satisfies the conditions:
which satisfies the conditions:![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
d)![]() , for some
, for some![]() ,
, ![]() and
and
![]() which satisfies the conditions:
which satisfies the conditions:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
e)![]() , where
, where![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() and satisfies the conditions:
and satisfies the conditions:![]() ,
,
![]() ,
, ![]() ,
,![]() ;
;
f)![]() , where,
, where, ![]() ,
,
![]() ,
, ![]() ,
, ![]() and satisfies the conditions:
and satisfies the conditions:![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
g)![]() , where
, where![]() ,
,
![]() ,
, ![]() ,
, ![]() , and satisfies the conditions:
, and satisfies the conditions:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
h)![]() , where
, where
![]() ,
, ![]() ,
, ![]() ,
, ![]() and satisfies the conditions:
and satisfies the conditions:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Proof. In this case from Lemma 2 it follows that diagrams 1-8 given in Figure 2 exhaust all diagrams of XI-subsemilattices of the semilattice D. A quasinormal representation of regular elements of the semigroup![]() , which are defined by these XI-semilattices, may have one of the form listed above. Then the validity of theorem immediately follows from ( [1] , Theorem 13.1.1, Theorem 13.3.1 and Theorem 13.7.1). □
, which are defined by these XI-semilattices, may have one of the form listed above. Then the validity of theorem immediately follows from ( [1] , Theorem 13.1.1, Theorem 13.3.1 and Theorem 13.7.1). □
Lemma 4. Let ![]() and
and![]() . Let
. Let ![]() be set of all regular elements of
be set of all regular elements of ![]() such that each element satisfies the condition of a) of Theorem 3. Then
such that each element satisfies the condition of a) of Theorem 3. Then![]() .
.
Proof. Let binary relation a of the semigroup ![]() satisfy the condition a) of Theorem 3. Then quasinormal representation of a binary relation a has a form
satisfy the condition a) of Theorem 3. Then quasinormal representation of a binary relation a has a form ![]() for some
for some![]() . It is easy to see that
. It is easy to see that ![]() for all
for all![]() , i.e. binary relation a is a regular element of the semigroup
, i.e. binary relation a is a regular element of the semigroup![]() . Therefore
. Therefore
![]() □
□
Now let binary relation a of the semigroup ![]() satisfy the condition b) of Theorem 3 (see diagram 2 of the Figure 3). In this case we have
satisfy the condition b) of Theorem 3 (see diagram 2 of the Figure 3). In this case we have ![]() where
where ![]() and
and![]() . By definition of the semi- lattice D it follows that
. By definition of the semi- lattice D it follows that
![]()
It is easy to see that there is only one isomorphism from ![]() to itself. That is
to itself. That is ![]() and
and![]() . If
. If
![]()
then
![]() (2)
(2)
Lemma 5. Let X be a finite set,
![]()
and![]() . Let
. Let ![]() be the set of all regular elements of
be the set of all regular elements of ![]() such that each element satisfies the condition b) of Theorem 3. Then
such that each element satisfies the condition b) of Theorem 3. Then
![]()
Proof. Let![]() ,
, ![]() ,
, ![]() and
and![]() . Then quasinormal representation of a binary relation a has a form
. Then quasinormal representation of a binary relation a has a form ![]() for some
for some ![]()
![]() ,
, ![]() and by state- ment b) of theorem 3 satisfies the conditions
and by state- ment b) of theorem 3 satisfies the conditions ![]() and
and![]() . By definition of the semilattice D we have
. By definition of the semilattice D we have ![]() and
and![]() , i.e.,
, i.e., ![]() and
and![]() . It follows that
. It follows that![]() . Therefore we have
. Therefore we have
![]() (3)
(3)
From this equality and by statement b) of Lemma 3 it immediately follows that
![]() □
□
Let binary relation a of the semigroup ![]() satisfy the condition c) of Theorem 3 (see diagram 3 of the Figure 3). In this case we have
satisfy the condition c) of Theorem 3 (see diagram 3 of the Figure 3). In this case we have![]() , where
, where ![]() and
and![]() . By definition of the semilattice D it follows that
. By definition of the semilattice D it follows that
![]()
It is easy to see ![]() and
and![]() . If
. If
![]()
then
![]() (4)
(4)
Lemma 6. Let X be a finite set,
![]()
and![]() . Let
. Let ![]() be the set of all regular elements of
be the set of all regular elements of ![]() such that each element satisfies the condition c) of Theorem 3. Then
such that each element satisfies the condition c) of Theorem 3. Then
![]()
where
![]()
Proof. Let ![]()
![]() be arbitrary element of the set
be arbitrary element of the set ![]() and
and![]() . Then quasinormal representation of a binary relation a has a form
. Then quasinormal representation of a binary relation a has a form ![]() for some
for some ![]()
![]() ,
, ![]() and by statement c) of Theorem 3 satisfies the conditions
and by statement c) of Theorem 3 satisfies the conditions![]() ,
, ![]() ,
, ![]() and
and![]() . By definition of the semilattice D we have
. By definition of the semilattice D we have![]() ,
,![]() . From this and by the condition
. From this and by the condition![]() ,
, ![]() ,
, ![]() ,
, ![]() we have
we have
![]()
i.e.![]() , where
, where![]() . It follows that
. It follows that![]() , From the last inclusion and by definition of the semilattice D we have
, From the last inclusion and by definition of the semilattice D we have ![]() for all
for all![]() , where
, where
![]()
Therefore the following equality
![]() (5)
(5)
holds. Now, let![]() ,
, ![]() and
and![]() . Then
. Then
for the binary relation a we have
![]()
From the last condition it follows that![]() .
.
1)![]() . Then we have that
. Then we have that![]() . But the inequality
. But the inequality ![]() contradicts the condition that representation of binary relation a is quasinormal. So, the equality
contradicts the condition that representation of binary relation a is quasinormal. So, the equality ![]() is true. From the last equality and by definition of the semilattice D we have
is true. From the last equality and by definition of the semilattice D we have ![]() for all
for all![]() , where
, where
![]()
2)![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() and
and ![]() are true. Then we have
are true. Then we have
![]()
and
![]()
respectively, i.e., ![]() or
or ![]() if and only if
if and only if
![]()
Therefore the equality ![]() is true. From the last equality and by definition of the semilattice D we have
is true. From the last equality and by definition of the semilattice D we have ![]() for all
for all![]() , where
, where
![]()
3)![]()
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() are true. Then we have
are true. Then we have
![]()
and
![]()
respectively, i.e., ![]() and
and ![]() if and only if
if and only if
![]()
Therefore the equality ![]() is true. From the last equality and by definition of the semilattice D we have
is true. From the last equality and by definition of the semilattice D we have
![]()
for all![]() , where
, where
![]()
Now, by equality (4) and conditions 1), 2) and 3) it follows that the following equality is true
![]()
where
![]() □
□
Lemma 7. Let![]() ,
, ![]() where
where ![]() and
and![]() . If quasinormal repre-
. If quasinormal repre-
sentation of binary relation a of the semigroup ![]() has a form
has a form ![]() for
for
some![]() ,
, ![]() and
and![]() , then
, then ![]() iff
iff
![]()
Proof. If![]() , then by statement c) of Theorem 3 we have
, then by statement c) of Theorem 3 we have
![]() (6)
(6)
From the last condition we have
![]() (7)
(7)
since ![]() by assumption.
by assumption.
On the other hand, if the conditions of (7) holds, then (6) immediately follows, i.e.![]() . Lemma is proved. □
. Lemma is proved. □
Lemma 8. Let![]() ,
, ![]() and X be a finite set. Then the following equality holds
and X be a finite set. Then the following equality holds
![]()
Proof. Let![]() , where
, where![]() . Assume that
. Assume that
![]() and a quasinormal representation of a regular binary relation a has a form
and a quasinormal representation of a regular binary relation a has a form ![]() for some
for some![]() ,
, ![]() and
and![]() . Then ac- cording to Lemma 7, we have
. Then ac- cording to Lemma 7, we have
![]() (8)
(8)
Further, let ![]() be a mapping of the set X in the semilattice D satisfying the conditions
be a mapping of the set X in the semilattice D satisfying the conditions ![]() for all
for all![]() .
.![]() ,
, ![]() ,
, ![]() and
and ![]() are the restrictions of the mapping
are the restrictions of the mapping ![]() on the sets
on the sets![]() ,
, ![]() ,
, ![]() ,
, ![]() respectively. It is clear that the intersection of elements of the set
respectively. It is clear that the intersection of elements of the set ![]() is an empty set, and
is an empty set, and![]() . We are going to find properties of the maps
. We are going to find properties of the maps![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
1)![]() . Then by the properties (1) we have
. Then by the properties (1) we have![]() , i.e.,
, i.e., ![]() and
and ![]() by definition of the set
by definition of the set![]() . Therefore
. Therefore ![]() for all
for all![]() .
.
2)![]() . Then by the properties (1) we have
. Then by the properties (1) we have![]() , i.e.,
, i.e., ![]() and
and ![]() by definition of the sets
by definition of the sets ![]() and
and![]() . Therefore
. Therefore ![]() for all
for all![]() .
.
By suppose we have that![]() , i.e.
, i.e. ![]() for some
for some![]() . If
. If![]() , then
, then![]() . Therefore
. Therefore![]() . That is contradiction to the equality
. That is contradiction to the equality![]() , while
, while ![]() by definition of the se- milattice D.
by definition of the se- milattice D.
Therefore ![]() for some
for some![]() .
.
3)![]() . Then by properties (1) we have
. Then by properties (1) we have![]() , i.e.,
, i.e., ![]() and
and ![]() by definition of the sets
by definition of the sets![]() ,
, ![]() and
and![]() . Therefore
. Therefore ![]() for all
for all![]() .
.
By suppose we have that![]() , i.e.
, i.e. ![]() for some
for some![]() . If
. If![]() , then
, then![]() . Therefore
. Therefore ![]() by definition of the set
by definition of the set ![]() and
and![]() . We have contradiction to the equality
. We have contradiction to the equality![]() .
.
Therefore ![]() for some
for some![]() .
.
4)![]() . Then by definition of a quasinormal representation of a binary relation a and by property (1) we have
. Then by definition of a quasinormal representation of a binary relation a and by property (1) we have![]() , i.e.
, i.e. ![]() by definition of the sets
by definition of the sets ![]() and
and![]() . There- fore
. There- fore ![]() for all
for all![]() .
.
We have seen that for every binary relation ![]() there exists ordered system
there exists ordered system ![]() . It is obvious that for disjoint binary relations there exist disjoint ordered systems.
. It is obvious that for disjoint binary relations there exist disjoint ordered systems.
Further, let
![]()
![]()
be such mappings that satisfy the conditions:
![]() for all
for all![]() ;
;
![]() for all
for all ![]() and
and ![]() for some
for some![]() ;
;
![]() for all
for all ![]() and
and ![]() for some
for some![]() ;
;
![]() for all
for all![]() .
.
Now we define a map f from X to the semilattice D, which satisfies the condition:
![]()
Further, let![]() ,
, ![]() ,
, ![]() and
and![]() . Then
. Then
binary relation ![]() may be represented by
may be represented by
![]()
and satisfies the conditions
![]() .
.
(By suppose ![]() for some
for some ![]() and
and ![]() for some
for some![]() ), i.e., by lemma 7 we have that
), i.e., by lemma 7 we have that![]() .
.
Therefore for every binary relation ![]() and ordered system
and ordered system ![]() there exists one to one mapping.
there exists one to one mapping.
By Lemma 1 and by Theorem 1 the number of the mappings ![]() are respectively
are respectively
![]()
Note that the number ![]() does not depend on choice of chains
does not depend on choice of chains
![]()
![]() of the semilattice D. Since the number of such different chains of the semilattice D is equal to 22, for arbitrary
of the semilattice D. Since the number of such different chains of the semilattice D is equal to 22, for arbitrary ![]() where
where![]() , the number of regular elements of the set
, the number of regular elements of the set ![]() is equal to
is equal to
![]() □
□
Therefore we obtain
![]() (9)
(9)
Lemma 9. Let X be a finite set, ![]() and
and![]() . Let
. Let ![]() be set of all regular elements of
be set of all regular elements of ![]() such that each element satisfies the condition c) of Theorem 3. Then
such that each element satisfies the condition c) of Theorem 3. Then
![]()
Proof. The given Lemma immediately follows from Lemma 6 and from the Equalities (5).
Now let a binary relation a of the semigroup ![]() satisfy the condition (d) of Theorem 3 (see diagram 4
satisfy the condition (d) of Theorem 3 (see diagram 4
of the Figure 3). In this case we have ![]() where
where ![]() and
and![]() . By de-
. By de-
finition of the semilattice D it follows that
![]()
It is easy to see ![]() and
and![]() . If
. If
![]()
then
![]() (10)
(10)
Lemma 10. Let X be a finite set,
![]()
and![]() . Let
. Let ![]() be set of all regular elements of
be set of all regular elements of ![]() such that each element satisfies the condition d) of Theorem 3. Then
such that each element satisfies the condition d) of Theorem 3. Then
![]()
Proof. Let![]() ,
, ![]() and
and![]() . Then
. Then
![]() , where
, where![]() ,
, ![]() and the following inclusions and inequalities are true
and the following inclusions and inequalities are true
![]()
From this it follows that
![]()
We consider the following cases.
1) ![]() or
or![]() . Then we have
. Then we have![]() . But the inequality
. But the inequality ![]() contradicts the condition that representation of binary relation a is quasinormal. So,
contradicts the condition that representation of binary relation a is quasinormal. So,
the equality ![]() holds. From the last equality and by definition of the semilattice D we have
holds. From the last equality and by definition of the semilattice D we have
![]() for all
for all![]() , where
, where
![]() (10a)
(10a)
2) ![]() or
or ![]() Then we have
Then we have ![]() or
or
![]() . But the inequality
. But the inequality ![]() or
or ![]()
contradicts the condition that representation of binary relation a is quasinormal. So, the equality ![]() holds. From the last equality and by definition of the semilattice D we have
holds. From the last equality and by definition of the semilattice D we have ![]() for all
for all![]() , where
, where
![]() (10b)
(10b)
By conditions (10a) and (10b) it follows that
![]()
From the last equality we have that the given Lemma is true. □
Now let a binary relation a of the semigroup ![]() satisfy the condition e) of Theorem 3 (see diagram 5 of the Figure 3). In this case we have
satisfy the condition e) of Theorem 3 (see diagram 5 of the Figure 3). In this case we have ![]() where
where ![]() and
and ![]() and
and![]() . By definition of the semilattice D it follows that
. By definition of the semilattice D it follows that
![]()
It is easy to see ![]() and
and![]() . If
. If
![]()
then
![]() (11)
(11)
Lemma 11. Let X be a finite set,
![]()
and![]() . Let
. Let ![]() be set of all regular elements of
be set of all regular elements of ![]() such that each element satisfies the condition e) of Theorem 3. Then
such that each element satisfies the condition e) of Theorem 3. Then
![]()
where
![]()
Proof. Let ![]() be arbitrary element of the set
be arbitrary element of the set ![]() and
and![]() . Then quasinormal representation of a binary relation a of the semigroup
. Then quasinormal representation of a binary relation a of the semigroup ![]() has a form
has a form
![]()
where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and by statement e) of Theorem 3 satisfies the following conditions
and by statement e) of Theorem 3 satisfies the following conditions
![]()
From this we have that the inclusions
![]()
are fulfilled. Therefore from the Equality (1) it follows that
![]() (12)
(12)
Let ![]() and
and ![]() be such elements of the set
be such elements of the set ![]() that
that ![]() and
and![]() . Then quasinormal representation of a binary relation a of the semigroup
. Then quasinormal representation of a binary relation a of the semigroup ![]() has a form
has a form
![]()
where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and by statement e) of Theorem 3 satisfies the following conditions
and by statement e) of Theorem 3 satisfies the following conditions
![]() ,
, ![]() ,
, ![]() and
and![]() .
.
Then by statement e) of Theorem 3 we have
![]()
From this conditions it follows that
![]()
For ![]() and
and ![]() we consider the following cases.
we consider the following cases.
1) ![]() or
or![]() . Then
. Then ![]() or
or ![]()
respectively. But the inequalities ![]() and
and ![]() contradict the condition that representation of binary relation a is quasinormal. So, the equality
contradict the condition that representation of binary relation a is quasinormal. So, the equality ![]() holds. From the last equality it follows that
holds. From the last equality it follows that ![]() for all
for all![]() , where
, where
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2) ![]() or
or![]() . Then by definition of the semilattice D it
. Then by definition of the semilattice D it
follows that the inequalities![]() ,
,
![]() or
or![]() ,
,
![]() are true respectively. But the inequalities
are true respectively. But the inequalities ![]()
and ![]() contradict the condition that representation of binary relation a is quasinormal. So,
contradict the condition that representation of binary relation a is quasinormal. So,
the equality ![]() holds. From the last equality, by definition of the semilattice D it follows
holds. From the last equality, by definition of the semilattice D it follows
that ![]() for all
for all![]() , where
, where
![]()
3) If![]() , then
, then
![]()
Then by definition of the semilattice D it follows that the inequalities
![]()
are true. But the inequalities ![]() contradict the condition that representation of binary relation a is quasinormal. So, the equality
contradict the condition that representation of binary relation a is quasinormal. So, the equality ![]() holds. From the last equality it follows that
holds. From the last equality it follows that![]() , where
, where
![]()
By similar way one can prove that ![]() for any
for any![]() .
.
4)![]() ,
, ![]() and
and ![]() are such elements of the set
are such elements of the set ![]() that
that![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() , then by statement e) of theorem 3 satisfies the following conditions:
, then by statement e) of theorem 3 satisfies the following conditions:
![]()
and
![]()
respectively, i.e., ![]() or
or ![]() if and only if
if and only if
![]()
Therefore, the equality ![]() is true. From the last equality by de- finition of the semilattice D it follows that
is true. From the last equality by de- finition of the semilattice D it follows that ![]() for all
for all![]() , where
, where
![]()
From the equalities ![]()
![]() and
and
![]()
![]() given above it follows that
given above it follows that
![]()
where
![]()
□
Lemma 12. Let ![]() and
and ![]() be arbitrary elements of the set
be arbitrary elements of the set![]() , where
, where![]() ,
, ![]() and
and![]() . If quasinormal representation of binary relation a
. If quasinormal representation of binary relation a
of the semigroup ![]() has a form
has a form![]() , for some
, for some
![]() ,
, ![]() ,
, ![]() and
and![]() , then
, then ![]() iff
iff
![]()
Proof. If![]() , then by statement e) of Theorem 3 we have
, then by statement e) of Theorem 3 we have
![]() (13)
(13)
From the last condition we have
![]() (14)
(14)
since ![]() and
and ![]() by supposition.
by supposition.
On the other hand, if the conditions of (14) hold, then the conditions of (13) follow, i.e.![]() .
.
□
Lemma 13. Let ![]() and
and ![]() be arbitrary elements of the set
be arbitrary elements of the set ![]() , where
, where![]() ,
, ![]() and
and![]() . Then the following equality holds:
. Then the following equality holds:
![]()
Proof. Let ![]() and
and ![]() be arbitrary elements of the set
be arbitrary elements of the set ![]() , where
, where![]() ,
, ![]() and
and![]() . If
. If![]() . Then quasinormal repre- sentation of a binary relation a of semigroup
. Then quasinormal repre- sentation of a binary relation a of semigroup ![]() has a form
has a form
![]()
for some![]() ,
, ![]() ,
, ![]() ,
, ![]() and by the lemma 12 satisfies the conditions
and by the lemma 12 satisfies the conditions
![]() (15)
(15)
Now, let ![]() be a mapping from X to the semilattice D satisfying the conditions
be a mapping from X to the semilattice D satisfying the conditions ![]() for all
for all![]() .
.![]() ,
, ![]() ,
, ![]() and
and ![]() are the restrictions of the mapping
are the restrictions of the mapping ![]() on the sets
on the sets ![]() respectively. It is clear that the intersection of elements of the set
respectively. It is clear that the intersection of elements of the set ![]() is an empty set and
is an empty set and
![]()
We are going to find properties of the maps![]() ,
, ![]() ,
, ![]() and
and![]() .
.
(1)![]() . Then by the properties (1) we have
. Then by the properties (1) we have
![]()
since ![]() i.e.,
i.e., ![]() and
and ![]() by definition of the set
by definition of the set![]() . Therefore
. Therefore ![]() for all
for all![]() .
.
(2)![]() . Then by the properties (1) we have
. Then by the properties (1) we have![]() , i.e.,
, i.e., ![]() and
and ![]() by definition of the set
by definition of the set ![]() and
and![]() . Therefore
. Therefore ![]() for all
for all![]() .
.
By suppose we have that![]() , i.e.
, i.e. ![]() for some
for some![]() . Then
. Then ![]() since
since![]() . If
. If![]() , then
, then![]() . Therefore
. Therefore![]() . That contradicts the equality
. That contradicts the equality![]() , while
, while ![]() and
and ![]() by definition of the semilattice D.
by definition of the semilattice D.
Therefore ![]() for some
for some![]() .
.
(3)![]() . Then by the properties (1) we have
. Then by the properties (1) we have![]() , i.e.,
, i.e., ![]() and
and ![]() by definition of the set
by definition of the set ![]() and
and![]() . Therefore
. Therefore ![]() for all
for all![]() .
.
By suppose we have that![]() , i.e.
, i.e. ![]() for some
for some![]() . Then
. Then ![]() since
since![]() . If
. If ![]() then
then![]() . Therefore
. Therefore![]() . That contradicts the equality
. That contradicts the equality![]() , while
, while ![]() and
and ![]() by definition of the semilattice D.
by definition of the semilattice D.
Therefore ![]() for some
for some![]() .
.
(4)![]() . Then by definition quasinormal representation of a binary relation a and by property (1) we have
. Then by definition quasinormal representation of a binary relation a and by property (1) we have![]() , i.e.
, i.e. ![]() by definition of the sets
by definition of the sets![]() ,
, ![]() and
and![]() . Therefore
. Therefore ![]() for all
for all![]() .
.
Therefore for every binary relation ![]() there exists ordered system
there exists ordered system![]() . It is obvious that for disjoint binary relations there exists disjoint ordered systems.
. It is obvious that for disjoint binary relations there exists disjoint ordered systems.
Further, let
![]()
![]()
be such mappings, which satisfy the conditions
![]() for all
for all![]() ;
;
![]() for all
for all ![]() and
and ![]() for some
for some![]() ;
;
![]() for all
for all ![]() and
and ![]() for some
for some![]() ;
;
![]() for all
for all![]() .
.
Now we define a map f from X to the semilattice D, which satisfies the condition
![]()
Further, let![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and
![]() . Then binary relation
. Then binary relation ![]() may be represented by
may be represented by
![]()
and satisfies the conditions
![]()
(By suppose ![]() for some
for some ![]() and
and ![]() for some
for some![]() ), i.e., by lemma 12 we have that
), i.e., by lemma 12 we have that![]() . Therefore for every binary relation
. Therefore for every binary relation ![]() and ordered system
and ordered system ![]() there exists one to one mapping.
there exists one to one mapping.
The number of the mappings![]() ,
, ![]() ,
, ![]() and
and ![]()
![]() are respectively
are respectively
![]()
Note that the number ![]() does not depend on choice of
does not depend on choice of
elements ![]() of the semilattice D, where
of the semilattice D, where![]() ,
, ![]() ,
, ![]() and
and![]() . Since the number of such different elements of the form
. Since the number of such different elements of the form ![]() of the semilattice D are equal to 24, the number of regular elements of the set
of the semilattice D are equal to 24, the number of regular elements of the set ![]() is equal to
is equal to
![]()
Lemma 14. Let X be a finite set,
□![]()
and![]() . Let
. Let ![]() be set of all regular elements of
be set of all regular elements of ![]() such that each element satisfies thecondition e) of Theorem 3. Then
such that each element satisfies thecondition e) of Theorem 3. Then![]() , where
, where
![]()
and
![]()
Proof. The given Lemma immediately follows from Lemma 11 and Lemma 13.
□Let binary relation a of the semigroup ![]() satisfy the condition g) of Theorem 3 (see diagram 7 of the Figure 3). In this case we have
satisfy the condition g) of Theorem 3 (see diagram 7 of the Figure 3). In this case we have![]() , where
, where![]() ,
, ![]() and
and![]() . By definition of the semilattice D it follows that
. By definition of the semilattice D it follows that
![]()
It is easy to see ![]() and
and![]() . If
. If
![]()
(see Figure 4).
![]()
Figure 4. Diagram of all subsemilattices isomorphic to 7 in Figure 2.
Then
![]() (16)
(16)
Lemma 15. Let X be a finite set, ![]() and
and![]() . Let
. Let
![]() be set of all regular elements of
be set of all regular elements of ![]() such that each element satisfies the condition f) of Theorem 3. Then
such that each element satisfies the condition f) of Theorem 3. Then
![]()
Proof. Let![]() ,
, ![]() and
and ![]() . Then quasinormal representation of a binary relation a of the semigroup
. Then quasinormal representation of a binary relation a of the semigroup ![]() has a form
has a form
![]()
where![]() ,
, ![]() and
and ![]() and by statement f) of theorem 3 satisfies the following conditions
and by statement f) of theorem 3 satisfies the following conditions
![]()
From this conditions it follows that
![]()
For ![]() and
and ![]() we consider the following case.
we consider the following case.
![]() or
or![]() . Then
. Then
![]()
or
![]()
But the inequality ![]() and
and ![]() contradict the condition that representation of binary relation a is quasinormal. So, the equality
contradict the condition that representation of binary relation a is quasinormal. So, the equality ![]() holds. From the last equality by definition of the semilattice D it follows that
holds. From the last equality by definition of the semilattice D it follows that ![]() for all
for all![]() , where
, where
![]() (17)
(17)
Now by Equalities (16) and by condition (17) it follows that
![]()
By statement f) of Lemma 3 the given Lemma is true.
□Now let binary relation a of the semigroup ![]() satisfy the condition f) of Theorem 3 (see diagram 6 of the Figure 3). In this case we have
satisfy the condition f) of Theorem 3 (see diagram 6 of the Figure 3). In this case we have![]() , where
, where![]() ,
, ![]() and
and![]() . By definition of the semilattice D it follows that
. By definition of the semilattice D it follows that
![]()
It is easy to see ![]() and
and![]() . If
. If
![]()
(see Figure 5).
Then
![]()
Lemma 16. Let X be a finite set, ![]() and
and![]() . Let
. Let ![]() be set of all regular elements of
be set of all regular elements of ![]() such that each element satisfies the condition g) of Theorem 3. Then
such that each element satisfies the condition g) of Theorem 3. Then
![]()
Proof. Let![]() ,
, ![]() and
and ![]() . Then quasinormal representation of a binary relation a of the semigroup
. Then quasinormal representation of a binary relation a of the semigroup ![]() has a form
has a form
![]()
Figure 5. Diagram of all subsemilattices isomorphic to 6 in Figure 2.
![]()
where![]() ,
, ![]() and
and ![]() and by statement g) of Theorem 3 satisfies the following conditions
and by statement g) of Theorem 3 satisfies the following conditions
![]()
From this conditions it follows that
![]()
For ![]() and
and ![]() we consider the following cases.
we consider the following cases.
1) ![]() or
or![]() . Then
. Then
![]()
or
![]()
But the inequalities ![]() and
and ![]() contradicts the condition that repre- sentation of a binary relation a is quasinormal. So, the equality
contradicts the condition that repre- sentation of a binary relation a is quasinormal. So, the equality ![]() holds. From the last equality by definition of the semilattice D it follows that
holds. From the last equality by definition of the semilattice D it follows that ![]() for all
for all![]() , where
, where
![]()
2) ![]() or
or![]() . Then
. Then
![]()
or
![]()
But the inequalities ![]() and
and ![]() contradicts the condition that repre- sentation of a binary relation a is quasinormal. So, the equality
contradicts the condition that repre- sentation of a binary relation a is quasinormal. So, the equality ![]() holds. From the last equality by definition of the semilattice D it follows that
holds. From the last equality by definition of the semilattice D it follows that ![]() for all
for all![]() , where
, where
![]()
3) ![]()
![]() or
or ![]()
![]() . Then
. Then
![]()
or
![]()
But the inequalities ![]() and
and ![]() contradicts the condition that repre- sentation of a binary relation a is quasinormal. So, the equality
contradicts the condition that repre- sentation of a binary relation a is quasinormal. So, the equality ![]() holds. From the last equality by definition of the semilattice D it follows that
holds. From the last equality by definition of the semilattice D it follows that ![]() for all
for all![]() , where
, where
![]()
Now by conditions 1), 2) and 3) it follows that
![]()
By statement (g) of Lemma 3 the given Lemma is true.
□Let binary relation a of the semigroup ![]() satisfy the condition h) of Theorem 3 (see diagram 8 of the Figure 3). In this case we have
satisfy the condition h) of Theorem 3 (see diagram 8 of the Figure 3). In this case we have![]() , where
, where![]() ,
,![]() . By definition of the semilattice D it follows that
. By definition of the semilattice D it follows that
![]()
It is easy to see ![]() and
and![]() . If
. If
![]()
(see Figure 6).
Then
![]()
Lemma 17. Let X be a finite set, ![]() and
and![]() . Let
. Let![]() be set of all regular elements of
be set of all regular elements of ![]() such that each element satisfies the condition h) of Theorem 3. Then
such that each element satisfies the condition h) of Theorem 3. Then
![]()
Figure 6. Diagram of all subsemilattices isomorphic to 8 in Figure 2.
![]()
Proof. Let![]() , where
, where![]() ,
,
![]() ,
, ![]() and
and![]() . Then quasinormal representation of a
. Then quasinormal representation of a
binary relation a of the semigroup ![]() has a form
has a form
![]()
where![]() ,
, ![]() ,
, ![]() and by statement g) of Theorem 3 sa- tisfies the following conditions
and by statement g) of Theorem 3 sa- tisfies the following conditions
![]()
From this conditions it follows that
![]()
For ![]() and
and ![]() we consider the following case.
we consider the following case.
![]() . Then
. Then![]() . But the inequality
. But the inequality
![]() contradicts the condition that representation of binary relation a is quasinormal. So,
contradicts the condition that representation of binary relation a is quasinormal. So,
the equality ![]() holds. From the last equality by definition of the semilattice D it follows that
holds. From the last equality by definition of the semilattice D it follows that
![]() for all
for all![]() , where
, where
![]()
Therefore we have
![]()
By statement h) of Lemma 3 the given Lemma is true. □
Let us assume that
![]()
Theorem 4. Let![]() ,
,![]() . If X is a finite set and
. If X is a finite set and ![]() is a set of all regular elements of the semigroup
is a set of all regular elements of the semigroup ![]() then
then![]() .
.
Proof. This Theorem immediately follows from Theorem 2 and Theorem 3. □
Example 1. Let![]() ,
,
![]()
![]()
Then![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
![]()
We have![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Cite this paper
Yasha Diasamidze,Nino Tsinaridze,Neşet Aydn,Neşet Aydn,Ali Erdoğan, (2016) Regular Elements of Bx(D) Defined by the Class ∑1(X,10)-I. Applied Mathematics,07,867-893. doi: 10.4236/am.2016.79078
References
- 1. Diasamidze, Ya. and Makharadze, Sh. (2013) Complete Semigroups of Binary Relations. Cityplace Kriter, Country- Region Turkey, 520 p.
- 2. Diasamidze, Ya. and Makharadze, Sh. (2010) Complete Semigroups of Binary Relations. (Russian) Sputnik+, Cityplace Moscow, 657 p.
- 3. Diasamidze, Ya. (2002) To the Theory of Semigroups of Binary Relations. Proceedings of A. Razmadze Mathematical Institute, 128, 1-15.
- 4. Diasamidze, Ya. (2002) Right Units in the Semigroups of Binary Relations. Proceedings of A. Razmadze Mathematical Institute, 128, 17-36.
- 5. Diasamidze, Ya.I. (2003) Complete Semigroups of Binary Relations. Journal of Mathematical Sciences (New York), 117, 4271-4319.
http://dx.doi.org/10.1023/A:1025030132270
- 6. Diasamidze, Ya.I., Makharadze, Sh.I. and Diasamidze, I.Ya. (2008) Idempotents and Regular Elements of Complete Semigroups of Binary Relations. Algebra and Geometry. Journal of Mathematical Sciences (New York), 153, 481-494.
http://dx.doi.org/10.1007/s10958-008-9132-1
- 7. Makharadze, Sh., Aydin, N. and Erdogan, A. (2015) Complete Semigroups of Binary Relations Defined by Semilattices of the Class ∑1(X,10). Applied Mathematics, 6, 274-294.
http://dx.doi.org/10.4236/am.2015.62026
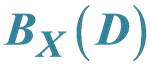 Defined by the Class
Defined by the Class 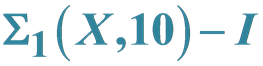




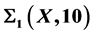 are studied. When X has finitely many elements, we have given the number of regular elements.
are studied. When X has finitely many elements, we have given the number of regular elements.
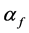 , denoted by
, denoted by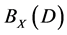 , is a subsemigroup of
, is a subsemigroup of 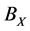 semigroup of all binary relations on X. (See [1] - [6] .)
semigroup of all binary relations on X. (See [1] - [6] .)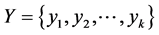 and
and 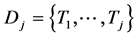 be two sets where
be two sets where 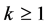 and
and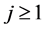 . Then the number
. Then the number 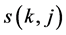 of all possible mappings from Y to subsets
of all possible mappings from Y to subsets 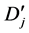 of
of 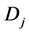 such that
such that 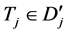 is given by
is given by




















































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































