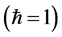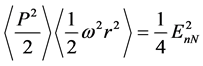Applied Mathematics
Vol.07 No.06(2016), Article ID:64939,10 pages
10.4236/am.2016.76047
Uncertainty Relations for Some Central Potentials in N-Dimensional Space
Sami M. AL-Jaber
Department of Physics, An-Najah National University, Nablus, Palestine

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 December 2016; accepted 21 March 2016; published 24 March 2016
ABSTRACT
We study the uncertainty relation for three quantum systems in the N-dimensional space by using the virial theorem (VT). It is shown that this relation depends on the energy spectrum of the system as well as on the space dimension N. It is pointed out that the form of lower bound of the inequality, which is governed by the ground state, depends on the system and on the space dimension N. A comparison between our result for the lower bound and recent results, based on information-theoretic approach, is pointed out. We examine and analyze these derived uncertainties for different angular momenta with a special attention made for the large N limit.
Keywords:
Heisenberg Uncertainty Relation, Central Potentials in N-Dimensions, Confined Particle, Hydrogen Atom, Harmonic Oscillator

1. Introduction
Generally, uncertainty relations form an important part in the foundations of quantum mechanics and play a crucial role in the development of quantum information and computation [1] [2] . These relations establish the existence of an irreducible lower bound for the uncertainty in the results of simultaneous measurements of non- commuting observables. In other words, the precision with which incompatible physical observables can be prepared is limited by an upper bound. In particular, the Heisenberg uncertainty principle (HUP) [3] represents one of the fundamental properties of a quantum system. It gives an irreducible lower bound on the uncertainty in the outcomes of simultaneous measurements of position and momentum. Originally, HUP came from a thought experiment about measurements of the position and momentum, but later Kennard [4] derived a mathematical formulation of HUP by considering inherent quantum fluctuations of position and momentum without any reference to measurement process and which was then generalized by Robertson [5] for arbitrary incompatible observables. Recently, Fujikawa [6] proposed a universally valid uncertainty relation which incorporated both the intrinsic quantum fluctuations and measurement effects. There has been a continual interest in utilizing HUP in different settings. For example, it has been used in the study of central potentials [7] - [11] and others consider its connection to geometry [12] [13] . Furthermore, it has been generalized to describe a minimal length as a minimal uncertainty in position measurement [14] - [18] through the modification of Heisenberg commutation relation into a generalized form. The existence of a minimal length has long been suggested in quantum gravity and string theory [19] - [24] , and has been proposed to describe, as an effective theory, non-point like particles like hadrons, quasi-particles or collective excitations [25] . In its original formulation, HUP is expressed in terms of variances of position and momentum of a particle. Such variances do not necessarily exist, and if they do, they describe the quantum probability distribution relative to a specific point of the probability domain. Therefore, various alternative formulations have been suggested by the use of information-theoretic uncertainty measures like the Shannon entropy [26] [27] , Renyi entropies [28] [29] , Tsallis entropies [30] , entropic moments [31] [32] and Fisher information [32] - [36] . During the past years, the generalization of three dimensional quantum problems to higher space dimensions receives a considerable development in theoretical and mathematical physics. For example, the central potentials, as hydrogen-like atoms [37] - [42] and harmonic oscillators [43] - [46] are being used as prototypes for other purposes in N-dimensional physics. Furthermore, the confined harmonic oscillator [45] and the confined hydrogen atom [47] have been discussed. The purpose of the present paper is to de-
rive and discuss the uncertainty product 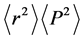 for three quantum systems in N-dimensional space: the harmonic oscillator, the hydrogen atom, and a confined particle in an impenetrable symmetrical spherical well.
for three quantum systems in N-dimensional space: the harmonic oscillator, the hydrogen atom, and a confined particle in an impenetrable symmetrical spherical well.
The lower bound for this product is analyzed and compared with other previous results that have been obtained by other methods. Our method is based on the virial theorem applied to the harmonic oscillator and the hydrogen atom systems to obtain the uncertainty product, while for the spherical well, the zeros of spherical Bessel functions are used for finding numerical results for the uncertainty product. Over the last years, the virial theorem technique has been employed in the study of physical quantities [48] [49] . Interesting features for the lower bound are discussed with a special attention explored for the large space dimension limit for the spherical well system. The organization of the paper is as follows: In section 2, we outline theoretical background. Then, we evaluate the uncertainty product for the harmonic oscillator quantum system in Section 3, for the hydrogen atom in Section 4, and for the spherical well in Section 5. We present conclusions and discussion of our work in Section 6.
2. Theoretical Background
The quantum mechanical state of a particle in the N-dimensional space with a central potential 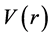 is governed by Schrödinger equation (setting
is governed by Schrödinger equation (setting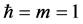 )
)
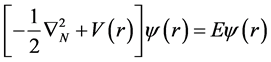 (1)
(1)
where 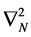 is the Laplacian operator on
is the Laplacian operator on 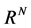 and is given by [50]
and is given by [50]
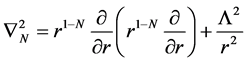 (2)
(2)
with 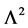 is a partial differential operator which depends on the angular coordinates
is a partial differential operator which depends on the angular coordinates
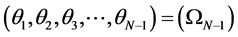
as
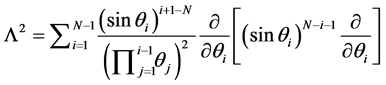 , (3)
, (3)
and satisfies [50]
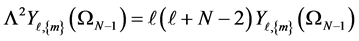 , (4)
, (4)
where 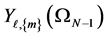 are the hyperspherical harmonics characterized by
are the hyperspherical harmonics characterized by 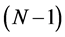 quantum numbers
quantum numbers 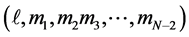 with the condition
with the condition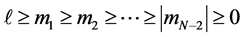 . The separation of variables yields the radial part of Schrödinger equation that satisfies
. The separation of variables yields the radial part of Schrödinger equation that satisfies
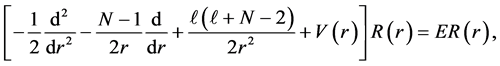
which, by letting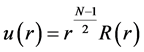
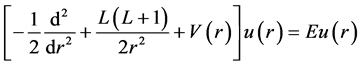
The above equation is the analogue to the one-dimensional Schrödinger equation with the grand orbital angular momentum, L given by
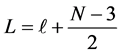
It is straight forward to write Equation (6) as
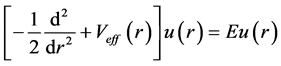
where the effective potential, 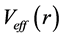

It is worth to note, as seen from Equation (7), the isomorphism between the space dimension N and the orbital angular momentum ℓ, which means that an orbital angular momentum 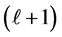
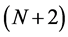
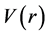
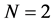
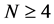
3. Isotropic Harmonic Oscillator in N-Dimensions
The potential for a harmonic oscillator is given by
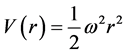
The virial theorem states that
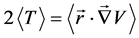
where T is the kinetic energy and the average is taken over an energy eigenstate of the system. The substitution of Equation (10) into Equation (11) gives

where the energy eigenvalues, 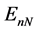
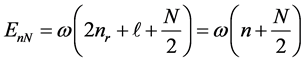
Using 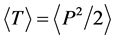
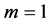
and thus the uncertainty product is
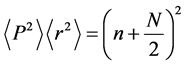
which obviously increases with both the quantum number n and the space dimension N. It is observed that the above product does not depend on the strength of the potential. The lower bound corresponds for the ground state 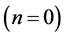
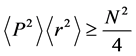
which saturates (equality is achieved) for nodeless harmonic oscillator wave function (ground state). Our results in Equation’s (14) and (15) are the same as those obtained by means of the Fisher’s information entropies [32] [33] , by Stamp’s principle [51] and by Shannon’s entropy [26] . Our method is more straight forward and simpler. The lower bound in Equation (15) reduces to the three-dimensional one, namely 9/4. Furthermore, our result in Equation (14) shows that the lower bound of the uncertainty product (for the ground state) in N-dimension is the
same as the lower bound of the 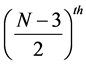
tainty product for a state with angular momentum 
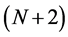
4. The Hydrogen Atom in N Dimensions
In this case, the potential is the coulomb potential,
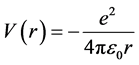
The application of the virial theorem gives 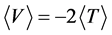
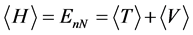
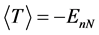
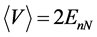

The energy eigenvalues for the eigenstates of a hydrogen atom in N dimensions are given by [37]
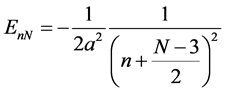
where a is Bohr radius. Therefore, 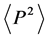
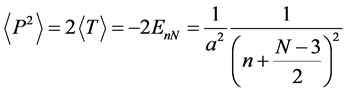
In order to find the average of the moments of position of different powers we use Kramer’s relation in N- dimensions [52]
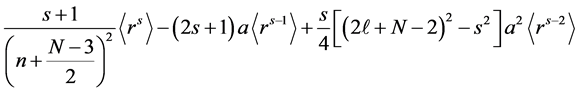
The successive application of the above relation for 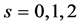

The above relation and Equation (18) yield the uncertainty product for position and momentum;
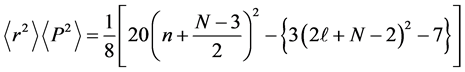
It is clear to notice that the uncertainty product increases as the quantum number n increases and decreases as the orbital angular momentum ℓ increases. One can easily verify that the uncertainty product increases as the space dimension increases.
The lower bound of the above uncertainty is achieved by setting 

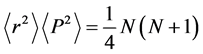
In what follows, we will consider the uncertainty product given in Equation (20) for some special cases:
1) For the three-dimensional case (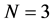
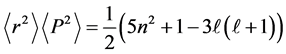
2) For any state n with ℓ has its maximum value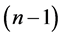
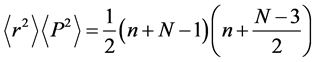
In this case, the uncertainty product has its minimum value since ℓ has its maximum value, which means the certainty has its highest value. This result is a natural consequence of the quantum centrifugal potential which tries to repel the particle away from the nucleus. In fact, it was pointed out by AL-Jaber [37] that the radial probability density has its maximum value when the orbital angular momentum has its maximum value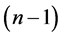
3) For any state n with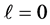

which corresponds to the maximum value of the uncertainty product, since ℓ has its minimum value. One may expect this result in the light of what we mentioned in the previous case.
4) The large space dimension limit: For large N, Equation (21) gives us the result
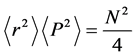
which is equal to the lower bound for the ground state of the harmonic oscillator in N-dimensions as we found in the previous section. This clearly shows that in the large N limit the lower bound for any state becomes saturated and equals to that of the ground state lower bound of the harmonic oscillator.
5) The uncertainty product difference between a state with 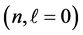
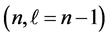
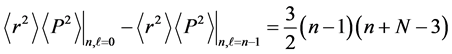
The above equation gives, for a given state n, the uncertainty product difference between minimum and maximum angular momenta for that state. This difference increases with both n, and N. This shows how much the particle becomes delocalized due to maximum orbital angular momentum.
6) Spherically symmetric infinite potential well
In this section, we consider a particle that is confined in an infinite impenetrable spherical well so that the potential is given by
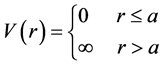
The substitution of the above potential into Equation (6) and letting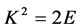
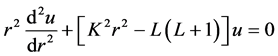
whose solution is the spherical Bessel function of order L, (the second solution has been dropped out since it diverges at the origin) and thus, the radial wave function is
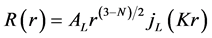
where AL is a normalization constant. The allowed energies can be obtained by requiring
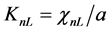
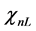
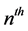
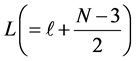
successive zeros of 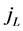
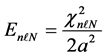
The integer n is the principal quantum number, which is the number of the root of spherical Bessel function in order of increasing magnitude. Since

On the other hand, the average value, 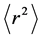
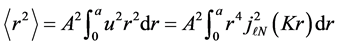
Following Grypeos [48] , we get

which, upon the substitution for L from Equation (7), becomes

The uncertainty product is now readily obtained using Equations (31) and (34), namely
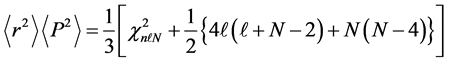
Again, the uncertainty product increases with both ℓ and N. The lower bound limit corresponds to ground state, 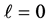
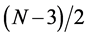
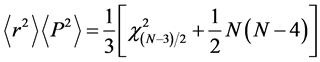
The above result shows that the uncertainty product increases with space dimension N, but is independent of the size of the well. It is instructive to calculate the above lower limit for different values of space dimension and compare its values with those for the harmonic oscillator and the hydrogen atom. This is shown in Table 1.
The numerical values for the lower bound for the three systems, presented in Table 1, show that the harmonic oscillator has the smallest values for all space dimension. We also note that the hydrogen atom has higher lower bound value than that of the spherical well for space dimension 3 and 4, but beyond that the spherical well has higher values than those for hydrogen atom.
Table 1. Lower bound for the uncertainty product for the spherical well, harmonic oscillator, and the hydrogen atom as function of space dimension N.
It is interesting to check the large N limit of the lower bound of these systems: For the hydrogen atom, the lower bound behaves as 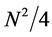

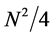
5. Conclusion
In this paper, we have derived the uncertainty product for position and momentum for harmonic oscillator, hydrogen atom, and spherically symmetric infinite well in N-dimensional space. We have found that this product depends on the orbital angular momentum and space dimension but independent of the strength of the potential. Our derivation relies on the virial theorem and Kramer’s relation for the harmonic oscillator and the hydrogen atom. Our results for the lower bound of the uncertainty product for each of the three systems agree with reported results for the three dimensional case. An interesting feature of our results is that in the large space dimension limit, the lower bound of the product for the hydrogen atom and the spherical well converge to that for the harmonic oscillator, namely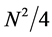
that the lower limit of the product in N-dimensions has the same value as that for the 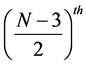
three dimensions. Furthermore, the product for a state with angular momentum 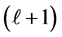

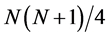
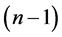
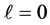
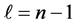
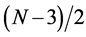
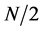

Cite this paper
Sami M.AL-Jaber, (2016) Uncertainty Relations for Some Central Potentials in N-Dimensional Space. Applied Mathematics,07,508-517. doi: 10.4236/am.2016.76047
References
- 1. Price, W.C. and Chissick, S.S. (1997) The Uncertainty Principle and Foundations of Quantum Mechanics. Wiley, New York.
- 2. Neilson, M.A. and Chuang, I.L. (2000) Quantum Computation and Quantum Information. Cambridge University Press, Cambridge.
- 3. Heisenberg, W. (1927) über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Zeitschrift für Physik, 43, 172-198.
http://dx.doi.org/10.1007/BF01397280 - 4. Kennard, E.H. (1927) Zur Quantenmechanik einfacher Bewegungstypen. Zeitschrift für Physik, 44, 326-352.
http://dx.doi.org/10.1007/BF01391200 - 5. Robertson, H.P. (1929) The Uncertainty Principle. Physical Review, 34, 163.
http://dx.doi.org/10.1103/PhysRev.34.163 - 6. Kujikawa, K. (2012) Universally valid Heisenberg Uncertainty Relation. Physical Review A, 85, Article ID: 062117.
http://dx.doi.org/10.1103/PhysRevA.85.062117 - 7. Kuo, C.D. (2005) The Uncertainties in Radial Position and Radial Momentum of an Electron in the Non-Relativistic Hydrogen-Like Atom. Annals of Physics, 316, 431-439.
http://dx.doi.org/10.1016/j.aop.2004.09.005 - 8. Chen, C.-Y., You, Y., Lu, F.-L. and Dong, S.-H. (2013) The Position-Momentum Uncertainty Relations for a Pöschl-Teller Type Potential and Its Squeezed Phenomena. Physics Letters A, 377, 1070-1075.
http://dx.doi.org/10.1016/j.physleta.2013.02.043 - 9. Rudnicki, L. (2012) Heisenberg Uncertainty Relations for Position and Momentum beyond Central Potentials. Physical Review A, 85, Article ID: 022112.
- 10. Bracher, C. (2011) Uncertainty Relations for Angular Momentum Eigenstates in Two and Three Spatial Dimensions. American Journal of Physics, 79, 313.
http://dx.doi.org/10.1119/1.3534840 - 11. Patil, S.H. and Sen, K.D. (2007) Uncertainty Relations for Modified Isotropic Harmonic Oscillator and Coulomb Potentials. Physics Letters A, 362, 109-114.
http://dx.doi.org/10.1016/j.physleta.2006.11.045 - 12. Kryukov, A. (2007) Geometric Derivation of Quantum Uncertainty. Physics Letters A, 370, 419-422.
http://dx.doi.org/10.1016/j.physleta.2007.09.038 - 13. Anastopoulos, C. and Savvidou, N. (2003) The Role of Phase Space Geometry in Heisenberg’s Uncertainty Relation. Annals of Physics, 308, 329-353.
http://dx.doi.org/10.1016/S0003-4916(03)00145-3 - 14. Akhoury, R. and Yao, V.P. (2003) Minimal Length Uncertainty Relation and the Hydrogen Spectrum. Physics Letters B, 572, 37-42.
http://dx.doi.org/10.1016/j.physletb.2003.07.084 - 15. Pedram, P. (2012) A Higher Order GUP with Minimal Length Uncertainty and Maximal Momentum II: Applications. Physics Letters B, 718, 638-645.
http://dx.doi.org/10.1016/j.physletb.2012.10.059 - 16. Pedram, P. (2012) Nonperturbative Effects of the Minimal Length Uncertainty on the Relativistic Quantum Mechanics. Physics Letters B, 710, 478-485.
http://dx.doi.org/10.1016/j.physletb.2012.03.015 - 17. Sprenger, M., Nicolini, P. and Bleicher, M. (2012) Physics on the Smallest Scales: An Introduction to Minimal Length Phenomenology. European Journal of Physics, 33, 853.
http://dx.doi.org/10.1088/0143-0807/33/4/853 - 18. Hassanabadi, H., Hooshnand, P. and Zarrinkamar, S. (2015) The Generalized Uncertainty Principle and Harmonic Interaction in Three Spatial Dimensions. Few-Body Systems, 56, 19-27.
http://dx.doi.org/10.1007/s00601-014-0910-7 - 19. Maggiore, M. (1994) Quantum Groups, Gravity, and the Generalized Uncertainty Principle. Physics Review D, 49, 5182.
http://dx.doi.org/10.1103/PhysRevD.49.5182 - 20. Maggiore, M. (1993) A Generalized Uncertainty Principle in Quantum Gravity. Physics Letters B, 304, 65-69.
http://dx.doi.org/10.1016/0370-2693(93)91401-8 - 21. Garay, L.J. (1995) Quantum Gravity and Minimum Length. International Journal of Modern Physics A, 10, 145-165.
http://dx.doi.org/10.1142/S0217751X95000085 - 22. Majumder, B. (2011) Quantum Black Hole and the Modified Uncertainty Principle. Physics Letters B, 701, 384-387.
http://dx.doi.org/10.1016/j.physletb.2011.05.076 - 23. Amati, D., Gialfaloni, M. and Veneziano, G. (1989) Can Spacetime Be Probed Below the String Size? Physics Letters B, 216, 41-47.
http://dx.doi.org/10.1016/0370-2693(89)91366-X - 24. Hossenfelder, S. (2013) Minimal Length Scale Scenarios for Quantum Gravity. Living Reviews in Relativity, 16, 2.
http://dx.doi.org/10.12942/lrr-2013-2 - 25. Brau, F. (1999) Minimal Length Uncertainty Relation and the Hydrogen Atom. Journal of Physics A: Mathematical and General, 32, 7691-7696.
http://dx.doi.org/10.1088/0305-4470/32/44/308 - 26. Bialynicki-Birula, I. and Mycielski, J. (1975) Uncertainty Relations for Information Entropy in Wave Mechanics. Communications in Mathematical Physics, 44, 129-132.
http://dx.doi.org/10.1007/BF01608825 - 27. Rudnicki, L., Sanchez-Moreno, P. and Dehesa, J.S. (2012) The Shannon-Entropy-Based Uncertainty Relation for D-Dimensional Central Potentials. Journal of Physics A: Mathematical and Theoretical, 45, Article ID: 225303.
http://dx.doi.org/10.1088/1751-8113/45/22/225303 - 28. Zozor, S. and Vigant, C. (2007) On Classes of Non-Gaussian Asymptotic Minimizers in Entropic Uncertainty Principles. Physica A, 375, 499-517.
http://dx.doi.org/10.1016/j.physa.2006.09.019 - 29. Zozor, S., Portesi, M. and Vigant, C. (2008) Some Extensions of the Uncertainty Principle. Physica A, 387, 4800-4808.
http://dx.doi.org/10.1016/j.physa.2008.04.010 - 30. Rajagobal, A.K. (1995) The Sobolev Inequality and the Tsallis Entropic Uncertainty Relation. Physics Letters A, 205, 32-36.
http://dx.doi.org/10.1016/0375-9601(95)00500-3 - 31. Massen, H. and Uffink, J.B.M. (1988) Generalized Entropic Uncertainty Relations. Physical Review Letters, 60, 1103-1106.
http://dx.doi.org/10.1103/PhysRevLett.60.1103 - 32. Toranzo, I.V., Lopez-Rosa, S., Esquivel, R.O. and Dehesa, J.S. (2015) Heisenberg-Like and Fisher-Information-Based Uncertainty Relations for N-Electron d-Dimensional Systems. Physical Review A, 91, Article ID: 062122.
http://dx.doi.org/10.1103/PhysRevA.91.062122 - 33. Sánchez-Moreno, P., González, R. and Dehesa, J.S. (2006) Improvement of the Heisenberg and Fisher-Information-Based Uncertainty Relations for D-Dimensional Central Potentials. New Journal of Physics, 8, 330.
http://dx.doi.org/10.1088/1367-2630/8/12/330 - 34. Romero, E., Sánchez, P. and Dehesa, J.S. (2006) Uncertainty Relation for Fisher Information of D-Dimensional Single-Particle Systems with Central Potentials. Journal of Mathematical Physics, 47, Article ID: 103504.
http://dx.doi.org/10.1063/1.2357998 - 35. Hamilton, L.P. and Mosna, R.A. (2010) Fisher Information and Kinetic Energy Functionals: A Dequantization Approach. Journal of Computational and Applied Mathematics, 233, 1542-1547.
http://dx.doi.org/10.1016/j.cam.2009.02.087 - 36. Gibilisco, P., Imparato, D. and Isola, T. (2007) Uncertainty Principle and Quantum Fisher Information. II. Journal of Mathematical Physics, 48, Article ID: 072109.
http://dx.doi.org/10.1063/1.2748210 - 37. AL-Jaber, S.M. (1998) Hydrogen Atom in N Dimensions. International Journal of Theoretical Physics, 37, 1289-1298.
http://dx.doi.org/10.1023/A:1026679921970 - 38. AL-Jaber, S.M. (2002) Ground-State Energy of the N-Dimensional Two-Electron Atoms. IL Nuovo Cimento B116, No.5 (2001), 593.
- 39. Kirchberg, A., Lange, J.D. and Wiph, A. (2003) Algebraic Solution of the Supersymmetric Hydrogen Atom in d Dimensions. Annals of Physics, 3003, 359-388.
http://dx.doi.org/10.1016/S0003-4916(03)00003-4 - 40. Nouri, S. (1999) Generalized Coherent States for the d-Dimensional Coulomb Problem. Physical Review A, 60, 1702-1705.
http://dx.doi.org/10.1103/PhysRevA.60.1702 - 41. AL-Jaber, S.M. and Lombard, R.J. (2005) Connection between the Spectrum and the Moments of the Ground-State Density in N-Dimensional Space. Journal of Physics A: Mathematical and General, 38, 4637-4644.
http://dx.doi.org/10.1088/0305-4470/38/21/009 - 42. AL-Jaber, S.M. (2013) Solution of the Radial N-Dimensional Schrödinger Equation Using Homotopy Perturbation Method. Romanian Journal of Physics, 58, 247-259.
- 43. Demirlap, E. (2005) Bound States of n-Dimensional Harmonic Oscillator Decorated with Dirac Delta Functions. Journal of Physics A: Mathematical and General, 38, 4783-4794.
http://dx.doi.org/10.1088/0305-4470/38/22/003 - 44. Ghosh, S. and Majhi, B.R. (2008) Crypto-Harmonic Oscillator in Higher Dimensions: Classical and Quantum Aspects. Journal of Physics A: Mathematical and Theoretical, 41, Article ID: 065306.
http://dx.doi.org/10.1088/1751-8113/41/6/065306 - 45. AL-Jaber, S.M. (2008) A Confined N-Dimensional Harmonic Oscillator. International Journal of Theoretical Physics, 47, 1853-1864.
- 46. Montgomery, H.E., Gampoy, G. and Aquino, N. (2010) The Confined N-Dimensional Harmonic Oscillator Revisited. Physica Scripta, 81, Article ID: 045010.
http://dx.doi.org/10.1088/0031-8949/81/04/045010 - 47. Shaqqor, M.A. and AL-Jaber, S.M. (2009) A Confined Hydrogen Atom in Higher Space Dimensions. International Journal of Theoretical Physics, 48, 2462-2472.
http://dx.doi.org/10.1007/s10773-009-0041-y - 48. Grypeos, M.E., Koutroulos, C.G., Oyewumi, K.J. and Petridou, T.A. (2004) The HVT Technique and the “Uncertainty” Relation for Central Potentials. Journal of Physics A: Mathematical and General, 37, 7895-7908.
http://dx.doi.org/10.1088/0305-4470/37/32/005 - 49. Grypeos, M.E., Koutroulos, C.G., Oyewumi, K.J. and Petridou, T.A. (2002) The HVT Technique and the Treatment of Two Basic Inequalities. Journal of Physics A: Mathematical and General, 35, 2223-2228.
http://dx.doi.org/10.1088/0305-4470/35/9/312 - 50. Avery, J. (2000) Hyperspherical Harmonics and Generalized Sturmians. Kluwer, Dordrecht.
- 51. Romera, E. (2002) Stam’s Principle D-Dimensional Uncertainty-Like Relationships and Some Atomic Properties. Molecular Physics, 100, 3325-3329.
http://dx.doi.org/10.1080/00268970210148778 - 52. Griffiths, D.J. (1995) Introduction to Quantum Mechanics. Prentice-Hall, New York.