Received 5 September 2015; accepted 24 October 2015; published 27 October 2015

ABSTRACT

In this paper, we establish the existence of at least four distinct solutions to an elliptic problem with singular cylindrical potential, a concave term, and critical Caffarelli-Kohn-Nirenberg exponent, by using the Nehari manifold and mountain pass theorem.

Keywords:

Singular Cylindrical Potential, Concave Term, Critical Caffarelli-Kohn-Nirenberg Exponent, Nehari Manifold, Mountain Pass Theorem

1. Introduction

In this paper, we consider the multiplicity results of nontrivial nonnegative solutions of the following problem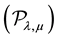

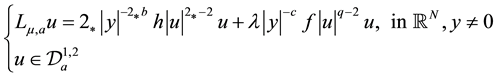
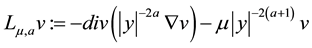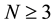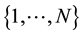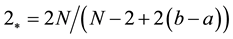
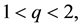
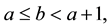
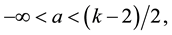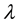
where, where each point x in is written as a pair where k and N are integers such that and k belongs to, is the critical Caffarelli-Kohn-Nirenberg exponent, , 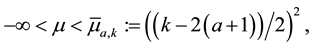is a real parameter, 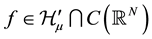, h is a bounded positive function on. is the dual of, where and will be defined later.

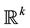Some results are already available for in the case, see for example [1] [2] and the references

therein. Wang and Zhou [1] proved that there exist at least two solutions for with,

and, under certain conditions on f. Bouchekif and Matallah [3] showed the

existence of two solutions of under certain conditions on functions f and h, when, , and, with a positive constant.

Concerning existence results in the case, we cite [4] [5] and the references therein. Musina [5] con- sidered with instead of a and, also with, , , with and. She established the existence of a ground state solution when and

for with instead of a and. She also showed that with, , does not admit ground state solutions. Badiale et al. [6] studied with, , and. They proved the existence of at least a nonzero nonnegative weak solution u, satis- fying when and. Bouchekif and El Mokhtar [7] proved that ad- mits two distinct solutions when, with, , and

where is a positive constant. Terracini [8] proved that there is no positive solutions of with, when, and. The regular problem corresponding to and has been considered on a regular bounded domain by Tarantello [9] . She proved that, for, the dual of, not identically zero and satisfying a suitable condition, the problem considered admits two distinct solutions.

Before formulating our results, we give some definitions and notation.

We denote by and, the closure of with respect to the norms

and

respectively, with for.

From the Hardy-Sobolev-Maz’ya inequality, it is easy to see that the norm is equivalent to. More explicitly, we have

for all.

We list here a few integral inequalities.

The starting point for studying, is the Hardy-Sobolev-Maz’ya inequality that is particular to the cylindrical case and that was proved by Maz’ya in [4] . It states that there exists positive constant such that

(1.1)

for any.

The second one that we need is the Hardy inequality with cylindrical weights [5] . It states that

(1.2)

It is easy to see that (1.1) hold for any in the sense

(1.3)

where positive constant, , , and in [10] , if the embedding is compact, where is the weighted space with norm

Since our approach is variational, we define the functional J on by

with

A point is a weak solution of the equation if it satisfies

with

Here denotes the product in the duality,.

Let

From [11] , is achieved.

Throughout this work, we consider the following assumptions:

(F) there exist and such that, for all x in.

(H)

Here, denotes the ball centered at a with radius r.

In our work, we research the critical points as the minimizers of the energy functional associated to the problem on the constraint defined by the Nehari manifold, which are solutions of our system.

Let be positive number such that

where.

Now we can state our main results.

Theorem 1. Assume that, , , (F) satisfied and verifying, then the system has at least one positive solution.

Theorem 2. In addition to the assumptions of the Theorem 1, if (H) hold and satisfying, then has at least two positive solutions.

Theorem 3. In addition to the assumptions of the Theorem 2, assuming, there exists a positive real such that, if satisfy, then has at least two positive solution and two opposite solutions.

This paper is organized as follows. In Section 2, we give some preliminaries. Sections 3 and 4 are devoted to the proofs of Theorems 1 and 2. In the last Section, we prove the Theorem 3.

2. Preliminaries

Definition 1. Let, E a Banach space and.

i) is a Palais-Smale sequence at level c ( in short) in E for I if

where tends to 0 as n goes at infinity.

ii) We say that I satisfies the condition if any sequence in E for I has a convergent sub- sequence.

Lemma 1. Let X Banach space, and verifying the Palais-Smale condition. Suppose that and that:

i) there exist, such that if, then;

ii) there exist such that and;

let where

then c is critical value of J such that.

Nehari Manifold

It is well known that J is of class in and the solutions of are the critical points of J which is not bounded below on. Consider the following Nehari manifold

Thus, if and only if

(2.1)

Note that contains every nontrivial solution of the problem. Moreover, we have the following results.

Lemma 2. J is coercive and bounded from below on.

Proof. If, then by (2.1) and the Hölder inequality, we deduce that

(2.2)

Thus, J is coercive and bounded from below on.

Define

Then, for

(2.3)

Now, we split in three parts:

We have the following results.

Lemma 3. Suppose that is a local minimizer for J on. Then, if, is a critical point of J.

Proof. If is a local minimizer for J on, then is a solution of the optimization problem

Hence, there exists a Lagrange multipliers such that

Thus,

But, since. Hence. This completes the proof.

Lemma 4. There exists a positive number such that for all, verifying

we have.

Proof. Let us reason by contradiction.

Suppose such that. Then, by (2.3) and for, we have

(2.4)

Moreover, by the Hölder inequality and the Sobolev embedding theorem, we obtain

(2.5)

and

(2.6)

From (2.5) and (2.6), we obtain, which contradicts an hypothesis.

Thus. Define

For the sequel, we need the following Lemma.

Lemma 5.

i) For all such that, one has.

ii) For all such that, one has

Proof. i) Let. By (2.3), we have

and so

We conclude that.

ii) Let. By (2.3), we get

Moreover, by (H) and Sobolev embedding theorem, we have

This implies

(2.7)

By (2.2), we get

Thus, for all such that, we have.

For each with, we write

Lemma 6. Let real parameters such that. For each with, one has the following:

i) If, then there exists a unique such that and

ii) If, then there exist unique and such that, , ,

Proof. With minor modifications, we refer to [12] .

Proposition 1 (see [12] )

i) For all such that, there exists a sequence in.

ii) For all such that, there exists a a sequence in.

3. Proof of Theorems 1

Now, taking as a starting point the work of Tarantello [13] , we establish the existence of a local minimum for J on.

Proposition 2. For all such that, the functional J has a minimizer and it satisfies:

i)

ii) is a nontrivial solution of.

Proof. If, then by Proposition 1 (i) there exists a sequence in, thus it bounded by Lemma 2. Then, there exists and we can extract a subsequence which will denoted by such that

(3.1)

Thus, by (3.1), is a weak nontrivial solution of. Now, we show that converges to strongly in. Suppose otherwise. By the lower semi-continuity of the norm, then either and we obtain

We get a contradiction. Therefore, converge to strongly in. Moreover, we have. If not, then by Lemma 6, there are two numbers and, uniquely defined so that and. In particular, we have. Since

there exists such that. By Lemma 6, we get

which contradicts the fact that. Since and, then by Lemma 3, we may assume that is a nontrivial nonnegative solution of. By the Harnack inequality, we conclude that and, see for exanmple [14] .

4. Proof of Theorem 2

Next, we establish the existence of a local minimum for J on. For this, we require the following Lemma.

Lemma 7. For all such that, the functional J has a minimizer in and it satisfies:

i)

ii) is a nontrivial solution of in.

Proof. If, then by Proposition 1 ii) there exists a, sequence in, thus it bounded by Lemma 2. Then, there exists and we can extract a subsequence which will denoted by such that

This implies

Moreover, by (H) and (2.3) we obtain

(4.1)

where,. By (2.5) and (4.1) there exists a positive number

such that

(4.2)

This implies that

Now, we prove that converges to strongly in. Suppose otherwise. Then, either . By Lemma 6 there is a unique such that. Since

we have

and this is a contradiction. Hence,

Thus,

Since and, then by (4.2) and Lemma 3, we may assume that is a nontrivial nonnegative solution of. By the maximum principle, we conclude that.

Now, we complete the proof of Theorem 2. By Propositions 2 and Lemma 7, we obtain that has two positive solutions and. Since, this implies that and are distinct.

5. Proof of Theorem 3

In this section, we consider the following Nehari submanifold of

Thus, if and only if

Firsly, we need the following Lemmas

Lemma 8. Under the hypothesis of theorem 3, there exist, such that is nonempty for any and.

Proof. Fix and let

Clearly and as. Moreover, we have

If for, for , then there exists

where

and

and there exists such that. Thus, and is nonempty for any.

Lemma 9. There exist M, positive reals such that

and any verifying

Proof. Let, then by (2.1), (2.3) and the Holder inequality, allows us to write

where. Thus, if

and choosing with defined in Lemma 8, then we obtain that

(5.1)

Lemma 10. Suppose and. Then, there exist r and posi- tive constants such that

i) we have

ii) there exists when, with, such that.

Proof. We can suppose that the minima of J are realized by and. The geometric conditions of the mountain pass theorem are satisfied. Indeed, we have

i) By (2.3), (5.1) and the fact that, we get

Exploiting the function and if, we obtain that for. Thus, there exist, such that

ii) Let, then we have for all

Letting for t large enough. Since

we obtain. For t large enough we can ensure.

Let and c defined by

and

Proof of Theorem 3.

If

then, by the Lemmas 2 and Proposition 1 ii), J verifying the Palais-Smale condition in. Moreover, from the Lemmas 3, 9 and 10, there exists such that

Thus is the third solution of our system such that and. Since is odd with res- pect u, we obtain that is also a solution of.

Cite this paper

Mohammed El MokhtarOuld El Mokhtar, (2015) On Elliptic Problem with Singular Cylindrical Potential, a Concave Term, and Critical Caffarelli-Kohn-Nirenberg Exponent. Applied Mathematics,06,1891-1901. doi: 10.4236/am.2015.611166

References