Applied Mathematics
Vol.06 No.12(2015), Article ID:61293,31 pages
10.4236/am.2015.612179
A Thermal-Hydraulic Coolant Channel Module (CCM) for Single- and Two-Phase Flow
Alois Hoeld
Retired from Gesellschaft fuer Anlagen- und Reaktorsicherheit (GRS), Munich, Germany

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 June 2015; accepted 17 November 2015; published 20 November 2015
ABSTRACT
A theoretical “drift-flux based thermal-hydraulic mixture-fluid coolant channel model” is presented. It is the basis to a corresponding digital “Coolant Channel Module (CCM)”. For this purpose derived “Separate-Region Mixture Fluid Approach” should yield an alternative platform to the currently dominant “Separate-Phase Models” where each phase is treated separately. Contrary to it, a direct procedure could be established with the objective to simulate in an as general as possible way the steady state and transient behaviour of characteristic parameters of single- and/or (now non-separated) two-phase fluids flowing within any type of heated or non-heated coolant channels. Their validity could be confirmed by a wide range of verification and validation runs, showing very satisfactory results. The resulting universally applicable code package CCM should provide a fundamental element for the simulation of thermal-hydraulic situations over a wide range of complex systems (such as different types of heat exchangers and steam generators as being applied in both conventional but also nuclear power stations, 1D and 3D nuclear reactor cores etc). Thereby the derived set of equations for different coolant channels (distinguished by their key numbers) as appearing in these systems can be combined with other ODE-s and non-linear algebraic relations from additional parts of such an overall model. And these can then to be solved by applying an appropriate integration routine. Within the solution procedure, however, mathematical discontinuities can arise. This due to the fact that along such a coolant channel transitions from single- to two-phase flow regimes and vice versa could take place. To circumvent these difficulties it will in the presented approach be proposed that the basic coolant channel (BC) is subdivided into a number of sub-channels (SC-s), each of them being occupied exclusively by only a single or a two-phase flow regime. After an appropriate nodalization of the BC (and thus its SC-s) and after applying a “modified finite volume method” together with other special activities the fundamental set of non-linear thermal-hydraulic partial differential equations together with corresponding constitutive relations can be solved for each SC separately. As a result of such a spatial discretization for each SC type (and thus the entire BC) the wanted set of non-linear ordinary differential equations of 1st order could be established. Obviously, special attention had to be given to the varying SC entrance or outlet positions, describing the movement of boiling boundaries or mixture levels along the channel. Including even the possibility of SC-s to disappear or be created anew during a transient.
Keywords:
Applied Mathematics, Non-Linear Partial Differential Equations of First Order, Thermal-Hydraulics of Single- and Two-Phase Flow, Separate-Region Mixture-Fluid Model Concept

1. Introduction
A large number of thermal-hydraulic (TH) models and, based on them, effective computer codes have been developed and are still in development being needed for the theoretical and computational description of heat and fluid transport along different types of sometimes very complex technical systems. Their objective is to describe both the steady state and transient behaviour of characteristic key parameters of a single- or two-phase fluid flowing along different types of loops of such a system in an adequate way. Various forms of heated or non- heated coolant channels play an important part within these loops. As, for example, being demanded in the most nuclear but also conventional power plants.
Due to the presence of discontinuities in the first principle of mass conservation of a two-phase flow model, caused at the transition from single- to two-phase flow and vice versa, it was obvious that the direct solution of the basic conservation equations for single and mixture fluid along such a coolant channel could get very complicated. Obviously many discussions have and will continue to take place among experts as to which sort of theoretical approach should be chosen for the correct description of such thermal-hydraulic two-phase problems when looking at the wide range of applications. What is thus the most appropriate way to deal with such a special thermal-hydraulic problem?
1.1. Separate-Phase Model Concept
With the introduction of a “Separate-Phase Model Concept” already very early an efficient way has been found how to circumvent such upcoming difficulties. This by proposing a solution method with the intention to separate the two-phases within the basic equations of such a mixture-flow either partially or even completely from each other. Hence, approaches where each phase is treated separately. This yields a system of 4, 5 or sometimes even 6 equations by splitting each of the conservation equations into two so-called “field equations”. Compared to the four independent parameters characterising the mixture fluid the separate-phase systems demand a much higher number of additional variables and often very speculative assumptions. This has the additional consequence that a number of very complex relations had to be incorporated into the theoretical description of such a module. An enormous amount of CPU-time has to be expended for the solution of the resulting sets of differential and analytical equations in a computer code.
Obviously, based on such assumptions, the interfacial relations both between the (heated or cooled) wall but also between each of the two phases have to be completely rearranged too. This raises the difficult question of how to describe in a realistic way the direct heat input into and between the phases and the movement resp. the friction of the phases between them. In such separate-phase approaches this problem is solved by introducing corresponding exchange (=closure) terms between the equations based on special transfer (=closure) laws. Since they can, however, not be based on fundamental laws or at least on experimental measurements this approach requires a significant effort to find an adequate formulation of the exchange terms between the phases. It must therefore be recognised that the quality of these basic equations (and especially their boundary conditions) will be intimately related to the (rather artificial and possibly speculative) assumptions adopted if comparing them with the original conservation laws of the basic 3-equation system and their constitutive equations as well. The problem of a correct description of the interfacial reaction between the phases and the wall remains. Hence, very often when comparing diverse separate-phase models with each other due to their underlying differing assumptions only very poor consistency between them can be stated.
Another problem arises from the fact that special methods have to be foreseen to describe the moving boiling boundary or mixture level (or at least to estimate their “condensed” levels) in such a mixture fluid (see, for example, the “Level Tracking” method in TRAC [1] ). Additionally, these methods show often deficiencies in describing extreme situations such as the treatment of single- and two-phase flow at the ceasing of natural circulation, the power situations if decreasing to zero etc. The codes are sometimes very inflexible, especially if they have to provide to a very complex physical system also elements which belong not to the usual class of “thermal-hydraulic coolant channels”. These can, for example, be nuclear kinetic considerations, heat transfer out of a fuel rod or through a tube wall, pressure build-up within a compartment, time delay during the movement of an enthalpy front along a downcomer, natural circulation along a closed loop, parallel channels, inner loops etc.
However, the “Separate-Phase Models” have become (despite of these difficulties) increasingly fashionable and dominant in the last decades of thermal-hydraulics as demonstrated by the widely-used codes TRAC [1] [2] , CATHENA [3] , RELAP [4] [5] , CATHARE [6] , ATHLET [7] [8] .
1.2. Separate-Region Mixture Fluid Model Concept
Obviously among other international institutes also at the Gesellschaft für Anlagen- und Reaktorsicherheit (GRS) at Garching/Munich very early activities within the scope of reactor safety research have been started with the aim to develop thermal-hydraulic models and digital codes which could have the potential to describe in a detailed way the overall transient and accidental behaviour of fluids flowing along a reactor core but also within the main components of different Nuclear Power Plant (NPP) types. For one of these components, namely the natural circulation U-tube steam generator together with its feedwater and main steam system an own theoretical model and a first version of the digital code UTSG [9] has been derived. Based on the experience of many years of application both at the GRS and a number of other institutes in different countries but also due to the rising demands coming from the safety-related research studies this UTSG theory and code has been continuously extended, ending finally in the establishment of a very satisfactory and mature code version UTSG-2 [10] . This could be used both in a stand-alone way but also as part of more comprehensive transient codes, such as the thermal-hydraulic GRS system code ATHLET [11] . Together with a high level simulation language GCSM (General Control Simulation Module) it could be taken care of a manifold of balance-of-plant (BOP) actions too.
During the research work for the development of an enhanced version of the code UTSG-2 it arose finally the idea to establish an own basic module which makes it possible to simulate the thermal-hydraulic mixture-fluid situation within any geometrical set-up of cooled or heated channels in an as general as possible way. This with the aim to be applicable for any modular construction of complex thermal-hydraulic assemblies of pipes and junctions. Thereby, in contrast to the above mentioned class of “separate-phase” modular codes and instead of separating the phases of a mixture fluid within the entire coolant channel an alternative theoretical approach has been foreseen, differing both in its form of application but also in its theoretical background.
Thereby a special and unique concept could be found how to circumvent the above mentioned difficulties due to discontinuities resulting from the spatial discretization of a coolant channel, arising eventually from nodes where a transition from single- to two-phase flow and vice versa can take place. By assuming each coolant channel to be seen as a (basic) channel (BC) which can, according to their different flow regimes, be subdivided into a number of sub-channels (SC-s). It is clear that each of these SC-s can consist of only two types of flow regimes. A SC with just a single-phase fluid, containing exclusively either sub-cooled water, superheated steam or supercritical fluid, or a SC with a two-phase mixture. The theoretical considerations of this “Separate-Region Approach” can then (within the class of mixture-fluid models) be appointed to only these two regimes. Hence, for each SC type, the “classical” three conservation equations for mass, energy and momentum can be treated in a direct way (and now without mathematical restrictions). In the case of a SC with mixture flow these basic equations had to be supported by a drift flux correlation (which should, however, also take care of stagnant or counter-current flow situations), yielding an additional relation for the appearing fourth variable, namely the steam mass flow.
The problem of the application of such an approach has thus shifted to the fact that now also varying SC entrance and outlet boundaries (marking the time-varying phase boundary positions) have to be considered. And causing in special situations the additional difficulty that along a channel such a SC can even disappear or be created anew. The solution procedure is based on the fact that after an appropriate nodalization of such a BC (and thus also it’s SC-s) a “modified finite volume method” (among others based on the Leibniz Integration Rule) had to be derived for the spatial discretization of the fundamental (non-linear) partial differential equations (PDE-s) of first order which represent the basic conservation equations of thermal-hydraulics for each SC.
Additionally, to link within the integration procedure the resulting mean nodal with their nodal boundary function values an adequate quadratic polygon approximation method (PAX) had to be established.
This special PAX method represents a central part of the here presented “Separate-Region Approach”. And this besides the suggestion to subdivide a (basic) channel into regions of different flow type, together with the very thoroughly tested packages for drift flux and single- and two-phase friction factors. Thus yielding an elegant method how to solve this essential thermal-hydraulic problem in a direct way.
The procedure should establish at the start of a calculation for each SC (and finally also the entire BC) a set of steady state non-linear algebraic equations and then for the following case of thermal-hydraulic transients at each time step the wanted set of non-linear ordinary differential equations (ODE-s) of 1-st order. All of them supported with their algebraic constitutive relations.
For more details see Section 8, comparing there these two approaches with each of them.
1.3. Remarks
The here presented article is part and the continuation of a publication series of three papers being already published in two INTECH Open Access Books ( [12] - [14] ). It is, according to a continuous research work, updated to the newest status in this field and concentrated in an advanced and very condensed form mainly to the theoretical background of this basic coolant channel model and to the special (and generally applicable) mathematical methods to solve this sort of resulting system of equations in a corresponding digital module.
2. Fundamental Equations for a Thermal-Hydraulic Drift-Flux Based Mixture Fluid Approach
Thermal-hydraulic single-phase or mixture-fluid models for coolant channels or their sub-channels are based on a number of fundamental physical laws, i.e., they obey genuine conservation equations for mass, energy and momentum. They are controlled at single-phase flow conditions by the three independent parameters: total mass flow G, temperature T and pressure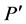 . For two-phase flow one more variable is asked, namely the total and steam mass flow G and GS, void fraction α and pressure
. For two-phase flow one more variable is asked, namely the total and steam mass flow G and GS, void fraction α and pressure . And they are supported by adequate constitutive equations, such as packages for thermo-dynamic and transport properties of water and steam, for single- and two-phase friction coefficients and (in case of two-phase flow) for drift flux.
. And they are supported by adequate constitutive equations, such as packages for thermo-dynamic and transport properties of water and steam, for single- and two-phase friction coefficients and (in case of two-phase flow) for drift flux.
2.1. Thermal-Hydraulic Conservation Equations
2.1.1. Mass Balance (Single- and Two-Phase Flow)
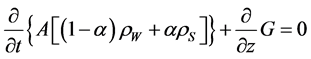 (1)
(1)
containing density terms 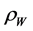 for sub-cooled or saturated water and
for sub-cooled or saturated water and 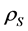 for saturated or superheated steam, the void fraction α and the cross flow area A which can (as discussed in Section 7) eventually be changing along the coolant channel. It determines, after a nodalization, the total mass flow
for saturated or superheated steam, the void fraction α and the cross flow area A which can (as discussed in Section 7) eventually be changing along the coolant channel. It determines, after a nodalization, the total mass flow 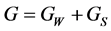 at node outlet in dependence of its node entrance values.
at node outlet in dependence of its node entrance values.
2.1.2. Energy Balance (Single- and Two-Phase Flow)
 (2)
(2)
with enthalpy terms hW for sub-cooled or saturated water and hS for saturated or superheated steam. As boundary values either the “linear power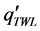 ”, the “heat flux
”, the “heat flux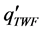 ” along the heated (or cooled) tube wall (with its heated perimeter UTW) or the local “power density term
” along the heated (or cooled) tube wall (with its heated perimeter UTW) or the local “power density term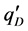 ” (transferred into the coolant channel with its cross Section A) are demanded to be known. The power terms having a positive sign if they are directed into the coolant (See also Sections 6.1, 6.4.2 and 9.1).
” (transferred into the coolant channel with its cross Section A) are demanded to be known. The power terms having a positive sign if they are directed into the coolant (See also Sections 6.1, 6.4.2 and 9.1).
2.1.3. Momentum Balance (Single- and Two-Phase Flow)
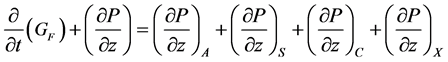 (3)
(3)
describing either the pressure differences (at steady state) or (in the transient case) the change in total mass flux 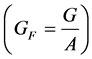 along a channel (See Section 6.5).
along a channel (See Section 6.5).
The general pressure gradient 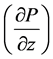 can be determined in dependence of terms for
can be determined in dependence of terms for
・ mass acceleration
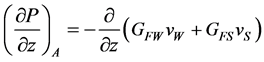 (4)
(4)
with vS and vW denoting steam and water velocities (definition see nomenclature)
・ static head
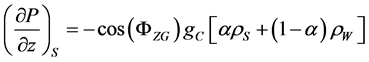 (5)
(5)
with 

・ the single- and/or two-phase friction relation

with a friction factor derived from corresponding constitutive equations (see Section 2.2.2) and finally
・ the direct perturbations 
2.2. Constitutive Equations
For the exact description of the steady state and the transient behaviour of single- or two-phase fluids a number of mostly empirical constitutive correlations are, besides the above mentioned conservation equations, demanded. To bring a structure into the manifold of existing correlations established by various authors, to find the best fitting ones for the different fields of application and to get a smooth transfer from one to another of them special and effective correlation packages had to be developed. Their validities can be and has been tested out-of-pile by means of adequate driver codes. Obviously, by means of this method improved correlations can easily be incorporated into the existing theory.
2.2.1. Thermodynamic and Transport Properties of Water and Steam
The different thermodynamic properties for water and steam (and their derivatives with respect to P and T, but also P and h) as demanded by the conservation and constitutive equations have to be determined by applying adequate water/steam tables. Additionally, since from the constitutive equations also the time-derivatives of these thermodynamic properties are asked which can be represented as

Corresponding thermodynamic transport properties such as the “dynamic viscosity” and “thermal heat conductivity” (and thus the “Prantl number”) are needed too. This is, for light-water systems, realized in the code packages MPP ( [15] , see also [12] ) containing the code packages MPPWS and MPPETA. All of them have been derived on the basis of tables given by [16] and [17] .
Obviously, the CCM code is also applicable for other coolant systems (heavy water, gas, oil) if adequate thermodynamic tables for this type of fluids are available.
2.2.2. Single- and Two-Phase Friction Factors
The friction factor fR needed in (6) can in case of single-phase flow be set, as proposed by [18] , equal to the Darcy-Weisbach single-phase friction factor.
The corresponding (Martinelli-Nelson) coefficient for two-phase flow has to be extended by means of a two-phase multiplier 
2.2.3. Drift Flux Correlation
Due to an additional independent variable appearing in the conservation Equations (1)-(3) for two-phase flow the set has to be completed by an additional relation. This can be achieved by any two-phase correlation, acting thereby as a “bridge” between GS and α. For example, by a slip correlation. However, to take care of stagnant or counter-current flow situations too an effective drift-flux correlation seemed here to be more appropriate. For this purpose an own package has been established, named MDS (see [20] - [23] ).
Regarding the different requirements in the application of CCM it turned out that it has many advantages to choose the Sonnenburg “flooding-based full-range” correlation [20] as applied for MDS. This correlation combines the common drift-flux procedure being formulated by Zuber-Findlay [24] and expanded by Ishii-Mishima [25] and (Ishii [26] ) etc. with the modern envelope theory. The correlation in the final package MDS had, however, to be rearranged in such a way that also the special cases of 

The resulting package MDS presents in case of a vertical non-heated or, for the case of low void fractions, heated wall (LHEATB = 0 or =1) a relation for the drift velocity vD with respect to the void fraction α

with respect to the (dimensionless) coefficient

and in combination with
・ adequate correlations for the phase distribution parameter C0 with their limit values if




and
・ relations for the limit velocities vSLIM and vWLIM dependent on α (independently of the total mass flow G, a fact which is important for the theory below)
All of them are also dependent on the input values “system pressure P”, the “hydraulic diameter
From the drift flux theory above finally also interrelations between different two-phase parameters can be established (now already in dependence of G) by starting from their definition equations. The steam mass flow (or flux) can, for example, be represented by

the steam velocity by


if introducing the coefficient

The relations of all the other characteristic two-phase parameters are given in more detail in [22] [23] . These could be the “phase distribution parameter








will play (as shown, for example, in (57)) an important part, if looking to the special situation that the entrance or outlet position of a SC can cross a BC node boundary (with 

For some application cases it seems to be reasonable to have the possibility to avoid counter-current flow (CCF) situations. This can be achieved by limiting within the general drift-flux theory the steam quality value of the X-α curve by a value XLIM which remains within the range

In a steady state situation then with respect to the solution possibilities of the basic (algebraic) set of equations the steam mass flow term GS has to act as an independent variable (instead of the void fraction α). The same is the case after an injection of a two-phase mixture coming from a “porous” channel or an abrupt change in steam mass flux GFS, as this can take place after a change in total mass flow or in the cross flow area at the entrance of a following BC. Then the total and the steam mass flow terms G and GS have to be taken as the basis for further two-phase considerations. The void fraction α and other two-phase parameters (vD, C0) can now be determined from an inverse (INV) form of this drift-flux correlation (with GS now as input).
3. Coolant Channel Geometry Data (BC and SC-s)
A “basic” coolant channel (BC) will be assumed to consists, as sketched in Figure 1, of a cylindrical tube of an as general as possible geometrical form, with its total length

tions



The theoretical considerations will, as already pointed-out, take advantage of the fact that, as sketched in Figure 1, a “basic” coolant channel (BC) can according to their flow regimes and (characterized by the logical LFTYPE) be subdivided into a number (NSCT) of sub-channels (SC-s). Each of these SC-s will be distinguished by their characteristic key numbers (NSC). Thereby it has, obviously, to be taken into account that their entrance and outlet SC-s can now have variable entrance and/or outlet positions.
Figure 1. Subdivision of a “basic channel (BC)” into “sub-channels (SC-s)” according to their flow regimes and their discretization.
As a consequence of the discretization of the BC each of the sub-channels (SC-s) is then subdivided too, now into a number of NCT SC nodes. Their geometry data are identical to the corresponding BC values, except, of course, at their entrance and outlet positions. The SC entrance position 



outlet position 


tion at the boiling boundary, a mixture level or the start position of a supercritical flow. Such a function follows from the given BC limit values and will, in the case of single-phase flow, be equal to the saturation temperature TSATCA or saturation enthalpies (














4. Mathematical Tools Needed for the Solution of (Non-Linear) PDE-s of 1st Order along a SC with Varying Entrance and Outlet Positions
For the realization of the theoretical thermal-hydraulic model in a corresponding digital code (module CCM) a special generally applicable integration procedures had to be derived.
4.1. Spatial Discretization of PDE-s of 1st Order (Modified Finite Element Method)
Based on the above presented nodalization the spatial discretization of the fundamental Equations (1)-(3) can be performed by means of a “modified finite element method”. This means that if a partial differential equation (PDE) of 1-st order having the general form with respect to a general solution function

is integrated over the length of a SC node three types of discretization elements can be expected:
・ Integrating a function 

・ Integrating over the gradient of a function 

and, finally,
・ Integrating over a time-derivative of a function (by applying the “Leibniz” rule)

This last rule plays for the here presented “separate-region mixture-fluid approach” an outstanding part. It allows (in combination with PAX) to determine in a direct way the time-derivatives of parameters which represent either a boiling boundary, mixture or a supercritical level. This procedure differs considerably from some of the “separate-phase methods” where, as already pointed out, very often only the collapsed levels of a mixture fluid can be calculated.
4.2. Quadratic Polygon Approximation Procedure PAX
According to the above described three different types of possible discretization elements the solution of the set of algebraic equations will in the steady state case yield directly function values (fNn) at node boundaries (zNn). On the basis of these values the also needed mean nodal functions (fMn) have then to be estimated by means of an adequate approximation procedure. On the other hand, the solution of the set of ordinary differential equations will (in the transient case) now yield the mean nodal functions fMn as a result of the integration. The also needed nodal boundary values fNn will then have to be estimated by the same procedure, now on the basis of fMn.
It is thus obvious that appropriate methods had to be developed which can help to establish relations between such mean nodal (fMn) and node boundary (fNn) function values. This is different to the “separate-phase” model approach where mostly a method is applied (called “upwind or donor cell differencing scheme”) with the mean parameter values to be shifted (in flow direction) to the node boundaries. In CCM a more ambitious approximation method is asked, giving to the entire procedure also a better “fine structure”. This is also demanded because, as to be seen later-on with regard to the relations of the Sections 6.2 to 6.4, not only absolute nodal SC boundary or mean SC nodal function values are required but as well also their nodal slopes 




Hence, for this purpose a special “quadratic polygon approximation” procedure, named “PAX”, had to be developed. It plays (together with the above presented Leibniz rule) an outstanding part in the development of the here presented “mixture-fluid model” and helps, in particular, to solve the difficult task of how to take care of varying SC boundaries (which can eventually cross BC node boundaries) in an appropriate and exact way.
4.2.1. Construction of an Adequate Approximation Function
The PAX procedure is based on the assumption that the solution function f(z) of a PDE (for example temperature or void fraction) along the SC part of a basic (=BC) coolant channel is split into a number of NCT nodal SC functions
・ The node entrance functions 

・ The mean function values fMn over each of the SC nodes have to be preserved (otherwise the balance equations could be hurt).
・ It is obvious that the gradients of the nodal entrance functions must not necessarily be equal to the gradients of the SC node outlets before (except for the last node entrance, i.e. at n = NCT). However, with the objective to guarantee stable behaviour of the approximated functions (for example in order to exclude “saw tooth-like behaviour” of them) it will, as a speciality of this approach, in an additional assumption be demanded that the outlet gradients of the first NCT - 1 nodes should be set equal to the slopes between their neighbour mean function values. The entrance gradient of the last node (n = NCT) should be either equal to the outlet gradient of the node before (if n = NCT > 1) or equal to a given SC input gradient (for the special case n = NCT = 1).
Thus one gets (together with relations resulting from the rearrangement of the definition equations)

This means, the corresponding approximation function do not reach only over the node n, its next higher one (n + 1) is included into the considerations. Except, of course, for the last one. There (in the case of NCT > 1) the quadratic approximation function (and thus also its corresponding approximation coefficients) are valid for both (the last and last but one) node.
The procedure has to take care also of the possibility that a SC can consist of only a single node (NCT = 1), with the (quadratic) approximation function having then to turn into a straight line. Hence, a special solution for such a single-node SC function is proposed, having the form

Thereby a variable slope is assumed which should) reflect two characteristic aspects. Namely to be, for the case that ΔzCA ® ΔzBA, equal to the slope (=gradient) 



These generally valid assumptions make the PAX procedure very effective (and stable). It is a conclusive onset in this method which helps to smooth the curve, guarantees that the gradients at the upper or lower SC boundary do not show abrupt changes for the case that a SC node boundary cross a BC one, avoids “saw-tooth” like behaviour of the parameters along the coolant channel and has the effect that perturbations at channel entrance do not directly affect corresponding parameters of the upper BC nodes.
4.2.2. Nodal Parameters Due to PAX
Mean nodal parameters resulting from PAX for the steady state case:
After having solved the basic set of non-linear algebraic equations (as presented later-on in the Sections 6.2 to 6.4) it is expected that as input to PAX the following nodal boundary parameters will have to be provided:
・ Geometry data such as the SC entrance (zCE) and node boundary positions (zNn) and thus also the SC outlet boundary zCA (as explained in Section 3) determining then in PAX the number of SC nodes (NCT),
・ The SC entrance function fN0 = fCE and (at least for the special case n = NCT = 1) its gradient
and
・ Finally the nodal boundary functions fNn (n = 1, NCT) with fCA = fNn at n = NCT (Note: fCA = fLIMCA if zCA < zBA).
Hence, with regard of inputs from steady state considerations the procedure PAX yields the wanted mean nodal function values

These functions can, in turn, then be applied as initial values for the transient case.
Nodal boundary parameters resulting from PAX as needed in the transient case:
After the integration of the set of non-linear ordinary differential equations (ODE-s) (as presented in the Sections 6.2 to 6.4) it can be expected that as input to PAX the SC outlet position (zCA = zNn) and thus also the total number NCT of SC nodes are directly available. Thereby it has to be distinguished (with regard to the transient situation) between two cases of possible input data sets available for PAX:
If this known SC outlet position is identical with the BC outlet (zCA = zBA) as input to PAX the mean nodal function values fMn for all NCT nodes (n = 1, NCT) are available
・ If this known SC outlet position is identical with the BC outlet (zCA = zBA) as input to PAX the mean nodal function values fMn for all NCT nodes (n = 1, NCT) are available
・ If this known SC outlet position is identical with the BC outlet (zCA = zBA) as input to PAX the mean nodal function values fMn for all NCT nodes (n = 1, NCT) are available
or, on the other hand,
・ if (due to the transient conditions) the SC outlet is moving within the BC (zCA < zBA) the corresponding SC outlet function is known, since restricted by a limit function, i.e. 
Hence, it follows for the transient case if the SC outlet is either moving within the BC

or, if not (and thus only for the last SC within the BC)

with fMn (n = 1, NCT) known from the integration procedure (except at n = NCT if zCA < zBA)
Final results for both cases:
All these nodal input function values can together with its input parameters fCE and the nodal positions zCE and zNn (at n = 1, NCT) then (in both cases) be applied as basic points for the PAX procedure. Yielding now, after rearranging the definition equations for the approximation functions in an adequate way, all the other not directly known nodal SC function parameters.
The slopes and gradients can finally be determined from (17), (18) and (20). They are indispensable for the special finite element method where they can due to the moving SC entrance or outlet boundaries cross BC
boundaries, i.e., their intervals can go to zero (

The corresponding time-derivative of the last mean node function which is needed for the determination of the SC boundary time-derivative (see Section 6.4) follows (as long as zCA < zBA) by differentiating (22)

with the coefficients


The time-derivative functions




to be estimated by establishing the time-derivatives of all the boundary functions at the nodes below NCT < 2. following a recursion procedure based on (22b).
4.2.3. Code Package PAX
Based on the above established set of equations a routine PAX had to be developed. Its objective was to calculate automatically either the nodal mean or nodal boundary values (in case of an either steady state or transient situation). The procedure should allow also determining the gradients and slopes at SC entrance and outlet (and thus also outlet values characterizing the entrance parameters of an eventually subsequent SC). Additionally, contributions needed for the calculation of the time-derivatives of the boiling boundary or mixture level can be gained (See later-on (70) and (71)).
Before incorporating the subroutine into the overall coolant channel module the validity of the presented PAX procedure has been thoroughly tested. By means of a special driver code (PAXDRI) different characteristic and extreme cases have been calculated. The resulting curves of such a characteristic example are plotted in Figure 2. It presents the two approximation curves of an artificially constructed void fraction distribution f(z) = α(z) along a SC with two-phase flow both for the steady state but also transient situation. The curves (on the basis of fMn and fNn) should be (and are) identical.
4.3. Decoupling of Mass and Energy Balance from Momentum Balance Equations
Treating the three conservation equations in a direct way would produce a set of “stiff” ODE-s. This is due to elements with fast pressure wave propagation (and thus being responsible for very small time constants). It has the consequence that their solution turns out to be enormously CPU-time consuming.
Hence, to avoid this costly procedure CCM has been developed with the aim to decouple the mass and energy from their momentum balance equations. This can be achieved by determining the thermodynamic properties of water and steam in the energy and mass balance equations on the basis of an estimated pressure profile P(z, t).
Figure 2. Approximation function f(z) along a SC for both steady state and transient conditions after applying PAX (example).
Thereby the pressure difference terms from a recursive (or a prior computational time step) will be added to an eventually time-varying system pressure PSYS(t), known from boundary conditions (See Section 6.5). After having solved the two conservation equations for mass and energy (now separately from and not simultaneously with the momentum balance) the different nodal pressure gradient terms can (by the then following momentum balance considerations) be determined according to (4)-(6).
It can additionally be assumed that according to the very fast (acoustical) pressure wave propagation along a coolant channel all the local pressure time-derivatives can be replaced by a given external system pressure time-derivative, i.e.,

By applying the above explained “intelligent” (since physically justified) simplification in CCM the small, practically negligible, error in establishing the thermodynamic properties on the basis of such an estimated pressure profile can be outweighed by the enormous benefit substantiated by two facts:
・ Avoidance of the very time-consuming solution of stiff equations,
・ The calculation of the mass flow distribution into different channels resulting from pressure balance considerations can, in a recursive way, be adapted already within each integration time step, i.e. there is no need to solve the entire set of differential equations for this purpose (See “closed channel” concept in Section 9.3).
5. BC Input Data Demanded by CCM
Besides the BC geometry data (as described in Section 3) obviously additional mostly BC function values are needed as inputs to CCM. Selected with the intention to apply only easily available BC values. They will then, within CCM, be automatically translated into corresponding SC values.
5.1. Initial Conditions
For the start of the transient calculations adequate steady state parameters have to be available as initial conditions.
5.2. Boundary Conditions and (Perturbation) Parameters at BC Entrance and/or Outlet
In the steady state case and especially (as boundary conditions) for transient calculations the following input parameters are expected to be known:
・ BC power profile. This means that either the nodal heat flux terms qFBE and qFBk (at BC entrance and each node k (=1, NBT).
or
・ qFBE and the nodal power terms QBMk are expected to be known, either directly from input or (as explained in Section 9.1) by solving the appropriate “Fourier heat conduction equation”. From the relation

then the other BC nodal terms (qFBk or QBMk, qLBk and qDBk) can be determined too [27] - [29] .
・ For normalization purposes at the starting calculation (i.e., at the steady state situation) as an additional parameter the total nominal (steady state) heat power QNOM,0 is asked.
・ Channel entrance temperature TBEIN (or enthalpy hBEIN)
・ System pressure PSYS and its time-derivative (dPSYS/dt), situated at a fixed position either along the BC (entrance, outlet) or even outside of the ensemble. Due to the fast pressure wave propagation each local pressure time-derivative can then be set equal to the change in system pressure (as described in Section 9.3).
・ Total mass flow GBEIN at BC entrance together with pressure terms at BC entrance PBEIN and outlet PBAIN. These three parameters are needed for steady state considerations (and partially used for normalization purposes). In the transient case only two of them are demanded as input. The third one will be determined automatically by the model. These allows then to distinguish between the situation of an “open” or “closed channel” concept as this will be explained in more detail in Section 9.3.
・ Steam mass flow GSBEIN at BC entrance (=0 or =GBEIN at single- or 0 < GSBEIN < GBEIN at two-phase flow conditions). The corresponding entrance void fraction αBE will then be determined automatically within the code by applying the inverse drift-flux correlation.
・ Eventually needed time-derivatives of such (perturbation) entrance functions can either be expected to be known directly from input or be estimated from their absolute values.
By choosing adequate boundary conditions then also thermal-hydraulic conditions of special situations can be simulated. For example, that of several channel assembles (of nuclear power plants, test loops etc.) which can consist of a complex web of pipes and branches (represented by different BC-s, all of them distinguished by their key numbers KEYBC). Obviously, also the case of an ensemble consisting of inner loops (as this is needed if describing parallel channels in a reactor core) can be treated in an adequate way by applying the concept of a “closed channel” procedure (see Section 9.3).
6. Theoretical Thermal-Hydraulic Separate-Region Approach
6.1. Power Profile along a SC
Knowing from input (as explained in Section 5.2) the nodal BC power QBMk together with the linear power term qLBE at BC entrance then also the corresponding power profile along each of the SC-s can be determined.
Hence, if assuming linear behaviour of the “linear nodal BC power terms” within the corresponding BC nodes it follows for the
“nodal linear SC power” term

and the “nodal SC power term”

In the transient case the SC outlet position zCA (and thus the length ΔzCA of its last node) is (for the case zCA < zBA) directly known from the integration procedure, i.e., QMCA follows then directly from the relation above. For steady state conditions it follows, on the other hand, now the term QMCA,0 directly from energy balance considerations ((44) and (63)) and the term ΔzCA,0 can now, in a reverse manner, be calculated as shown in (69)).
And finally one gets for the
“mean nodal” and “nodal boundary SC power density” terms


This terms are, since independent of ΔzNn, very useful for the solution of special relations where ΔzNn→ 0 (as demanded later-on by (36) and (53)).
Hence, the “total SC power” can be presented as

6.2. SC with Single-Phase Fluid (LFTYPE > 0)
Transient situation
The spatial integration of the two PDE-s of the conservation Equation (1) and Equation (2) over a (single-phase) SC node n yields (by taking into account the rules from Section 4.1, the relations from (7) and (27), the possibility of a locally changing nodal cross flow area along the BC and the fact that eventually VMn → 0) for the transient case relations for
・ the total nodal mass flow

and, if eliminating by inserting from the equation above the term GNn into the discretized energy balance equation
・ the time-derivative of the mean nodal coolant temperature:

containing the (also for the special situation of 


and the coefficients






In the transient case the mean nodal coolant temperature value TMn is at the begin of each (intermediate) time step known. This either from steady state considerations (in combination with PAX) or as a result of the integration procedure. Hence, other characteristic parameters needed in the relations above can be determined too. From the PAX procedure it follow also the SC nodal terms 



Among other results also the SC outlet position zCA is provided by the integration procedure, allowing then to determine the total number of SC nodes (NCT) too. The situation that zCA = zBA means the SC nodal boundary temperature values have, within the entire BC, not yet reached their limit values (TLIMNn = TSATNn) and NCT = NBCA with NBCA = NBT − NBCE. Otherwise, if zCA < zBA, this limit is reached (at node n), then NCT = n. Obviously, the procedure above yields also the time-derivative of the SC outlet position moving within this channel (As described in Section 6.4).
Steady state
The steady state part of the total nodal mass flow (charaterized by the index 0) follows from the basic non-linear algebraic Equation (34) if setting there the time-derivative equal to 0:

Treating (35) in a similar way and multiplying the resulting relation by VMn,0 yields the steady state nodal temperature resp. enthalpy terms

restricted by their saturation values. Then, as needed in (30) which results from energy balance considerations, the nodal power term for the last SC node has to obey the relation

Thus, for the steady state case, NCT is fixed too:

with similar relations for the case LFTYPE = 2.
From the resulting steady state enthalpy value hNn,0 then (by using the thermodynamic water/steam tables) the corresponding coolant temperature value TNn,0 follows (with TNn,0 = TSATNn,0 if n = NCT and zCA < zBA) and, by applying the PAX procedure, their mean nodal temperature and enthalpy values TMn,0 and hMn,0, parameters which are needed as start values for the transient calculations. Obviously, due to the non-linearity of the basic steady state equations, this procedure has to be performed in a recursive way.
It can additionally be stated that both the steady state and transient two-phase mass flow parameters get the trivial form


6.3. SC with Mixture Fluid (LFTYPE = 0)
The spatial integration of the two PDE-s of the conservation) Equation (1) and Equation (2) (now over the mixture-phase SC nodes n) can be performed by again taking into account the rules from Section 4.1, the relations from (7) and (27), by considering the possibility of locally changing nodal cross flow areas along the BC) and the fact that eventually VMn → 0. This yields then relations for
・ the total nodal mass flow term

with the coefficients (by neglecting thereby the small differences between mean and nodal saturation thermodynamic values)

and

・ the mean nodal void fraction time-derivative

and the coefficients




It can also be expected that at begin of each (intermediate) time step the mean nodal void fraction values 




If, in the transient case, the SC nodal boundary void fraction αNn does (within the entire BC) not reach its limit value (αLIMNn = 1 or 0) the total number of SC nodes is given as NCT = NBT − NBCE and zNn (at n = NCT) = zCA= zBT. Otherwise, if this limit is reached (at node n) then NCT = n and αNn = 1 (or =0) with zCA (
With regard to the drift-flux package [21] a relation for the steam mass flow gradient (as already derived in (13)) is required. It is based on the form

Eliminating in (49) the term 

The resulting “auxiliary” mass flow term GXn refers only to already known values (for example the power profile or parameters from the node before) and is thus directly available

A similar relation can be established from the drift flux correlation (10) by taking advantage of the fact that the needed drift velocity vDNn and the phase distribution parameter C0Nn are independent from the total mass flow GNn (and can thus be determined before knowing GNn). This term (GNn) results then by combining (58) and (10)

using the coefficient

All other characteristic two-phase parameters follow then from the drift flux correlation package [22] and [23] . These are especially the nodal steam mass flow GSNn and, eventually, the slope 


Obviously, at a mixture flow situation the mean nodal temperature and enthalpy terms are equal to their saturation values

and are only dependent on their local pressure value.
Relations for the steady state case follow by setting in (49) and (52) (resp. (53)) the time-derivatives equal to 0. For the total mass flow parameters a similar relation as already given for the single-phase flow (see (52)) is valid, yielding GNn,0 = GBE,0.
Hence, one obtains a relation for the (steady state) nodal steam mass flow

if knowing the term QMCA,0 = QMn,0 at n = NCT (see (30)).
Thus the total number (NCT) of SC nodes can be determinrd too:

and also the corresponding steam quality parameter

The nodal boundary void fraction values αNn,0 can now be determined by applying the inverse drift-flux correlation. The mean nodal void fraction value αMn,0 from the PAX procedure. All of them are needed as starting values for the transient calculation.
6.4. SC Entrance and Outlet Boundaries
6.4.1. SC Entrance Position
The SC entrance position zCE (=zNn at n = 0) is (for both the steady state but also transient case) either equal to BC entrance zBE (for the first SC within the BC) or equal to the outlet boundary of the SC before (See also Section 3).
6.4.2. SC Outlet Position
Steady state:
The SC (steady state) outlet position zCA,0 (=zNn at n = NCT), i.e. the boiling boundary zBB,0 or mixture level zML,0, can for the trivial case of 

Otherwise, the length of the last (SC) node (ΔzCA,0) and thus also

can be determined if taking into account that the corresponding steady state total number NCT of nodes of a (single- or two-phase) SC is already determined by (46) or (64). The nodal power term QMCA,0 of the last SC node are then given by (45) or (63). Hence, if dividing (30) by ΔzBkqLBk − 1,0 yields an algebraic quadratic equation of the form

yielding finally as solution

Then, from the relations in Section 6.1, also the other characteristic steady state power terms can be calculated.
Transient situation:
The transient SC outlet boundary zCA (=boiling boundary or mixture level) follows, as already pointed-out, directly from the integration procedure. Thus also ΔzCA and NCT are determined. A boundary which can move along the entire BC (and thereby also cross BC node boundaries). A SC can even shrink to a single node (NCT = 1), start to disappear or to be created anew. Then, if ΔzCA → 0, in the relations above the slope in the vicinity of such a boundary has to be replaced by a gradient (determined in PAX).
The mean nodal coolant temperature or, if LFTYPE = 0, void fraction of the last SC node is interrelated by the PAX procedure with the locally varying SC outlet boundary zCA. Hence, in a transient situation the time-derivative of only one of these parameters is demanded. The second one follows then after the integration from the PAX procedure.
If combining (in case of single-phase flow) (24) and (35) the wanted relation for the SC boundary time derivative can be expressed by

and if taking for the case of a mixture flow in a similar way (24) and (52) into account

If zCA < zBA, the corresponding time-derivatives 

inserting the terms above into (35) or (52). After the integration procedure then the SC outlet boundary zCA (=boiling boundary zBB or mixture level zML) and thus also the total number NCT of SC nodes are given.
Similar considerations can thus yield alkso corresponding relations for the time-behaviour of a supercritical fluid.
6.5. Pressure Profile along a SC (and thus also BC)
After having solved the mass and energy balance equations, separately and not simultaneously with the momentum balance, the now exact nodal SC and BC pressure difference terms (


and the part

comprising, as described in Section 2.1.3, terms from static head (ΔPSBT), mass acceleration (ΔPABT), wall friction (ΔPFBT) and external pressure accelerations (ΔPXBT due to pumps or other perturbations from outside) and an (only for transient situations needed) term, ΔPGBT, being represented as

This last term describes the influence of time-dependent changes in total mass flux along a BC (caused by the direct influence of changing nodal mass fluxes) and can be estimated by introducing a “fictive” mean mass flux term GFBMT (averaged over all NSCT SC-s of the entire BC) with

Its time derivative can then be represented by

Looking at the available friction correlations, there arises the problem how to consider correctly contributions from spacers, tube bends, abrupt changes in cross sections etc. as well. The entire friction pressure decrease (ΔPFBT) along a BC can thus never be described in a satisfactory manner solely by analytical expressions. To minimize these uncertainties a further friction term, ΔPDBT, had to be included into these considerations.
Since the total steady state BC pressure difference ΔPBT,0 = ΔPPBT,0 is known from input the corresponding steady state additive pressure difference term ΔPDBT,0 is (according to (73) and (74)) fixed. It seems, however, to be reasonable to treat this term as a “friction” (or at least the sum with ΔPFBT) and not as a “driving” force. Thus it must be demanded that these terms should remain negative. Otherwise, input terms such as the entire pressure difference along the BC or corresponding friction factors have to be adjusted in an adequate way.
Describing the general additive pressure difference term ΔPDBT as to have the form

means that ΔPDBT is either supplemented with a direct additive term (index FADD) or the friction part is provided with a multiplicative factor (fFMP,0 − 1). For the additive part it will be assumed to be the (1 − εDPZ)-th part of the total additional pressure difference term and to be proportional to the square of the total coolant mass flow, e.g., at BC entrance

with the input coefficient εDPZ = εDPZI governing from outside which of them should prevail.
From the known steady state total “additional” term ΔPDBT,0 the corresponding additive friction factor fADD,0 follows then directly from the equation above. From (77) then the multiplicative one

There arises now the question how the validity of both correction factors could be expanded to the transient case too. In the here presented approach this is done by assuming that these factors should remain time-inde- pendent, i.e., that fADD = fADD,0 and fFMP = fFMP,0. This allows finally also to determine the wanted nodal pressure decrease term ΔPDBT of (73) for the transient case.
By adding the resulting nodal BC pressure difference terms to the (time-varying) system pressure PSYS(t), given from outside as boundary condition with respect to a certain position (in- or outside of the BC), then finally also the absolute nodal pressure profile PBk along the BC can be established (This term is needed at the begin of the next time step within the constitutive equations).
7. Digital Coolant Channel Module CCM
Starting from the above presented “drift-flux based mixture-fluid theory” an universally applicable (1D) thermal-hydraulic coolant channel module, named CCM, could be established. It was derived with the intention to provide the authors of different and sometimes very complex multi-channel thermal-hydraulic codes with a general and easily applicable tool needed for the simulation of the steady state and transient behaviours of the most important single- and two-phase parameters along any type of heated or cooled coolant channel.
For the realization of the theoretical thermal-hydraulic model in the corresponding (digital) module CCM very specific methods had to be achieved by taking into account the following points:
・ The code has to be easily applicable, demanding only a limited amount of directly available input data. It should yield as output all the necessary time-derivatives and constitutive parameters of the basic coolant channels required for the establishment of an overall thermal-hydraulic code.
・ It was the intention of CCM to act as a complete system in its own right, requiring only BC (and not SC) related, and thus easily available input parameters (geometry data, initial and boundary conditions, parameters resulting from the integration etc.). The partitioning of BC-s into SC-s is done at the beginning of each recursion or time-step automatically within CCM, so no special actions are required of the user.
・ The quality of such a model is very much dependent on the method by which the problem of the varying SC entrance and outlet boundaries can be solved. Especially if they cross BC node boundaries during their movement along a channel. For this purpose a special “modified finite element-method” has been developed which takes advantage of the “Leibniz” rule for integration.
・ For the support of the nodalized differential equations along different SC-s a “quadratic polygon approximation” procedure (PAX) was constructed in order to interrelate the mean nodal with the nodal boundary functions. Providing additionally also nodal entrance gradients which are required for the calculation of varying SC entrance and outlet boundaries (See Section 4.2).
・ Several correlation packages such as, for example, packages for the thermodynamic properties of water and steam, single- and two-phase friction coefficients and drift flux correlations had to be developed and implemented (See Sections 2.2.1 to 2.2.3). And, for the case that the power distribution along the channel is not directly available also a heat transfer correlation package (See Section 9.1).
・ Knowing the characteristic parameters at all SC nodes (within a BC) then the single- and two-phase parameters at all node boundaries of the entire BC can be determined. And, in the transient case, also the corresponding time-derivatives of the characteristic averaged parameters of coolant temperatures resp. void fraction over these nodes. This yields a final set of (steady-state) algebraic resp. ODE-s and constitutive equations.
・ In order to be able to describe also thermodynamic non-equilibrium situations it can be assumed that each phase is represented by an own with each other interacting BC. For these purpose in the model the possibility of a variable cross flow area along the entire channel had to be considered as well.
Within the CCM procedure two further aspects play an important role. They are, however, not essential for the development of mixture-fluid models but can help enormously to enhance the computational speed and applicability of the resulting code when simulating natural circulation within a complex net of coolant pipes:
・ The solution of the energy and mass balance equations at each intermediate time step will be performed independently from momentum balance considerations (Section 4.3). Hence the heavy CPU-time consuming solution of stiff equations can be avoided.
・ The decoupling allows then also the introduction of an “open” and “closed channel” concept (see Section 9.3). Such a special method can be very helpful in describing complex physical systems with eventually inner loops. As an example see in [27] [28] , the simulation of a 3D compartment by parallel channels.
・ It represents thus a valuable and very generally applicable tool for the establishment of complex thermal-hydraulic computer codes. And this by being able to describe any physical system containing a variety of complicated single- and mixture fluid regions. Which can be represented by a number of different types of (basic) coolant channels. It provides automatically an overall set of nodal non-linear algebraic resp. ordinary differential equations and corresponding constitutive relations needed for each of these sub-channels and thus basic channels. Hence, this direct method can then be seen as a real counterpart to the currently preferred and dominant “separate-phase models”.
The application of a direct mixture-fluid technique follows a long tradition of research efforts. Ishii [26] , a pioneer of two-fluid modelling, states with respect to the application of effective drift-flux correlation packages in thermal-hydraulic models: “In view of the limited data base presently available and difficulties associated with detailed measurements in two-phase flow, an advanced mixture-fluid model is probably the most reliable and accurate tool for standard two-phase flow problems”. There is no new knowledge available to indicate that this view is invalid.
For more details about the construction of the module CCM see [29] - [34] and [13] .
8. Comparison between the “Separate-Region” and “Separate-Phase” Concepts
The here presented theoretical “separate-region” approach can thus disclose a new way in describing thermal- hydraulic problems. The resulting “mixture-fluid” technique can be regarded as a very appropriate way to circumvent the uncertainties apparent from the separation of the phases in a mixture flow. The starting equations are the direct consequence of the original fundamental physical laws for the conservation of mass, energy and momentum, supported by well-tested heat transfer and single- and two-phase friction correlation packages (and thus avoiding also the sometimes very speculative derivation of the “closure” terms). In a very comprehensive study [27] , a variety of arguments for the here presented type of approach is given.
Generally, the mixture-fluid approach is in line with Fabic [36] who names three strong points arguing in favour of this type of drift-flux based mixture-fluid models:
・ the application of (genuine) constitutive equations have the advantage that these relations are supported by a wealth of test data,
・ they do not require unknown or untested closure relations concerning mass, energy and momentum exchange between phases (they are mostly very speculative, influencing thus the reliability of the codes),
・ they are much simpler to apply,
and, it can be added,
・ discontinuities during phase changes can be avoided by having to concentrate to SC-s with one fluid type only and by deriving special solution procedures for the simulation of the movement of the SC entrance and outlet boundaries,
・ the possibility to circumvent a set of “stiff” ODE-s saves an enormous amount of CPU time which means that the other parts of the code can be treated in much more detail.
In contrast to the currently very dominant separate-phase models, the existing theoretical inconsistencies in describing a two-phase fluid flowing along a coolant channel if changing between single-phase and two-phase conditions and vice versa can be circumvented in the “separate-region” mixture-fluid approach presented here in a very elegant way. A very unique technique has been established built on the concept of subdividing a basic channel (BC) into different sub-channels (SC-s), thus yielding exact solutions of the basic drift-flux supported conservation equations. This type of approach shows, as discussed in [27] , distinct advantages vs. “separate phase” codes, especially if being aware of
・ the quality of the fundamental equations with basic conservation equations on the one side following directly from physical laws supported by experimentally based constitutive equations vs. split “field” equations on the other side with artificial closure terms,
・ the special solution methods due to the detailed interpolation procedure from PAX allowing to calculate the exact movement of boiling boundaries and mixture (or dry-out) levels, different to the “donor-cell averaging” methods yielding mostly only “condensed” levels,
・ the easy replacement of new and improved correlations within the different packages without having to change the basic equations of the theory (for example the complicated exchange terms of a “separate-phase” approach) ,
・ the possibility to take advantage of the “closed-channel concept” for an overall system (as explained in the next section), This concept can, for example, be needed for thermal-hydraulic 3D considerations, allowing thus to decouple a characteristic (“closed”) channel from other parts of a complex system of loops,
・ the speed of the computation,
・ the derivation of the theory in close and parallel connection with the establishment of the planned code by incorporating demands coming from both sides,
・ its easy applicability,
・ thermal non-equilibrium situations can be taken care too because of the introduction of varying cross sections along the BC into the concept. Two separate phases of such a fluid can then be simulated by two with each other interacting basic channels (for example if injecting sub-cooled water rays into a steam dome).
・ the maturity of the module, which is continuously enhanced by new application cases.
・ taking advantage of the considerable effort that has been done in verifying and checking CCM (besides an extensive V & V procedure), with respect to the applicability and adjustment and also for very extreme situations
・ and the benefits coming from the fact that most of the development work for the coolant channel thermal-hydraulics has already been shifted to establishment the here presented module, including the special provisions for extreme situations such as stagnant flow, zero power or zero sub-cooling, test calculations for the verification and validation of the code etc.).
The existence of the resulting widely verified and validated module CCM represents an important basic element for the construction of a variety of other comprehensive thermal-hydraulic models and codes as well. Such models and modules can be needed for the simulation of the steady state and transient behaviour of different types of steam generators, of 3D thermal-hydraulic compartments consisting of a number of parallel channels (reactor cores, VVER steam generators etc.). It shows special advantages in view of the determination of the mass flow distribution into different coolant channels after non-symmetric perturbations (see [27] [28] ), a problem which is far from being solved in many of the newest 3D studies.
It has, however, to be noted that there exist essential differences in applying these two types of approaches. The modular codes (such as TRAC, RELAP, ATHLET etc.) combine the different parts of a complex physical system by means of special input prescriptions. Being thus more susceptible to input errors. In the here presented separate-region approach the very well tested-out module CCM yields only for each compartment the needed characteristic algebraic and differential equations for the overall code (e.g. UTSG-3). Which allows more flexibility in describing a complicated physical system but demands also from the user that he is competent in establishing digital codes.
9. Overall Thermal-Hydraulic Multi-Channel Model and Digital Code
In order to be able to incorporate CCM in an overall thermal-hydraulic multi-channel code the interaction between the different compartments of the (sometimes very) complex physical system has to be defined. For example the heat transfer by means of boundary conditions.
And it has to be considered how the inner circles within this system work. For this purpose usually three more conservation laws have to be taken into account. They yield the necessary initial and boundary conditions to CCM with CCM providing, vice versa, the feedbacks in return.
The first two laws, namely the volume and mass balance relations, allow then to calculate the transient behaviour of the water (and steam volume) and of the pressure (and thus also system pressure PSYS) within a fixed (but also even a changing) overall volume VT.
The third physical law is based on the (trivial) fact that the sum of all pressure decrease terms along a closed loop must be zero. And thus in the transient case the entire pressure difference of at least one of the BC-s within this chain of loops is fixed. This allows then to determine the absolute values of the mass flow profile along the entire loop (for example at least at the entrance to this special BC to determine.
9.1. Power Profile along a Coolant Channel (Heat Transport into and out of a BC)
The nodal BC heat power terms QBMk (and the corresponding density qBCE at BC entrance) into or out of the coolant are needed (as explained in Section 6.1) as boundary condition for the energy balance equation (2) for each of the channels.
These terms can either be directly available (as this is the case for electrically heated loops) or be provided from other parts of the overall system.
In this later case the nodal power distribution (and the wall temperature TTW) have to be determined by solving the adequate Fourier heat conduction equations (a PDE of 2-nd order) at each BC node. Demanding thereby adequate boundary condition, such as, for example,

for the case of heat transfer out of a fuel rod resp. out or into a U-tube (with respect to a coolant having the temperature T). Such a procedure is, for example, presented in [13] [30] for the case of heat conduction through a U-tube wall).
For this purpose adequate heat transfer coefficients (αTW) are demanded. This means a method had to be found for getting these coefficients along a coolant channel at different flow regimes. In connection with the development of the UTSG code (and thus also of CCM) an own very comprehensive heat transfer coefficient package, called HETRAC [37] , has been established.
Obviously, since the resulting set of heat transfer coefficients can never represent the reality in a correct way the wetted surface of the involved heat transfer elements has, in view of the given nominal total steady state power value QNOM,0, to be provided with a corresponding correction factor. A factor which will be assumed to remain unchanged also in the transient case.
This classic method is different to a “separate-phase” concept where it has to be assumed that the heat is transferred both directly from the wall to each of the two possible phases but also exchanged between them. There arises then the question how the corresponding heat transfer coefficients for each phase should look like.
9.2. Mass and Volume Balance along the Entire Overall System
Calculating, as explaine above, the transient behaviour of the water (and steam volume) and of the system pressure PSYS. Together with the local pressure difference termss then also the pressure profile along each corresponding BC can be determined.
9.3. BC Entrance Mass Flow (“Open and Closed Channel Concept”)
It can be expected that at steady state conditions for each BC in a consecutive arrangement of BC-s the two pressure entrance and outlet values (PBE = PBEIN, PBA = PBAIN and the entrance mass flow GBE = GBEIN are known from input. The entire friction pressure decrease along a BC can, however, never be described in a satisfactory manner solely by analytical expressions as based only on the available friction correlations. Hence (as explained already in Section 6.3) in order to consider correctly contributions from spacers, tube bends, abrupt changes in cross sections etc. as well correction terms fFMP,0 and ΔPFADD,0 had to be introduced. In the case of parallel channels one of them will be taken as the representative one. Since it can usually be assumed that all these channels will have a common friction behaviour (otherwise a special procedure has to be foreseen), the correction factors for this channel can be assumed to be valid for all the other channels too This allows then to calculate also the different mass flow distribution into these channels (See for example [29] ).
In the transient case only two of the three characteristic variables (BC entrance mass flow, BC entrance and outlet pressure) can be expected to be known from input. Hence, in these considerations it will have to be distinguished between two special concepts. Is the mass flow at a BC entrance known as input, either as outside perturbation (resulting from a pump) or as an outlet value from a BC below) Yes or not? Assuming that in both cases the resulting (steady state) correction factors will remain unchanged then in the 1-st (“normal”) case (called the “Open Channel Concept”) the mass flow and pressure development along the channel (and thus also the missing pressure term at ether BC outlet or entrance) can be determined in the usual way (See Section 3). In the other case (named “Closed Channel Concept”) there has, however, to be found a method how to estimate an appropriate entrance mass flow value (or its time-derivative) by adjusting it to the given now fixed BC pressure difference.
This last case plays an important role in the simulation of the natural circulation behaviour of masses within the closed loops of complex physical systems. Due to the fact that the sum of the entire pressure decrease terms along such a closed circuit must be zero. Then the pressure difference (and thus also the absolute entrance and outlet values) are at least of one of the BC channels are defined. And with special methods the needed coolant mass flow terms can be determined
Usually, in the common thermal-hydraulic codes (see for example the “separate-phase” approaches) this problem is handled by solving the three (or more) fundamental equations for the entire complex system simultaneously. A procedure which affords mostly immense computational times and costs. In the here presented module (based on a separate treatment of momentum from mass and energy balance) a more elegant method could be established. Thus introducing an additional very efficient aspect into the theory of CCM.
This last and still very provisional method has been applied within the UTSG-3 code [13] for the simulation of the natural-circulation behaviour of the secondary steam generator loop. Similar considerations have been undertaken for a 3D case where the automatic mass flow distribution into different entrances of a set of parallel channels is asked (See e.g. [28] [29] ). The experience of such calculations should help to decide which of the different possible procedures should finally be given preference.
The “open/closed channel concept” makes sure that measures with regard to the entire closed loop do not need to be taken into account simultaneously but (for each channel) separately. Its application can be restricted to only one “characteristic” channel of a sequence of channels of a complex loop. This additional tool of CCM can in such cases help to handle the variety of closed loops within a complex physical system in a very comfortable way.
10. Solution Procedure
10.1. Steady State
The characteristic steady state parameters are determined in a direct way, i.e. calculated by setting all the time- derivatives equal to zero and solving the resulting set of non-linear algebraic equations for SC-s (as being presented in the Sections 6.2, 6.3 and 6.4). Thereby, due to the nonlinearities in the set of the (steady state) constitutive equations a recursive procedure in combination with and controlled by the main program has to be applied until a certain convergence in the solution vectors can be stated. The results are then combined to BC parameters and transferred again back to the main (=calling) program.
The (seemingly trivial) demand that the solution vectors should remain unchanged at the begin of calculation and still zero-power conditions is a very valuable and important check of the quality of the set of transient basic equations.
10.2. Transient Situation
For the transient case, as a result of the integration (performed within the calling program and thus outside of CCM) the solution parameters of the set of ODE-s are transferred after each intermediate time step to CCM. These are (as described in detail also in Section 7) mainly the mean nodal SC and thus BC coolant temperatures, mean nodal void fractions and the resulting boiling or superheating boundaries. These last two parameters allow then to subdivide the BC into SC-s number (NCT) of SC nodes. Finally, the needed SC (and thus BC) time-derivatives can then be determined within CCM yielding the corresponding constitutive parameters and the total and nodal length (zNn and ΔzNn) of these SC-s and thus also their total (as described in the Sections 6.2 to 6.4) and then transmitted again to the calling program where the integration for the next time step can take place.
11. Natural-Circulation Thermal-Hydraulic U-Tube Steam Generator Code UTSG-3
The construction of such an overall code has, for example, be exercised by establishing a new and advanced version of UTSG, now called UTSG-3, being based, similarly as in the previous code UTSG-2, on the same U-tube system layout (heat transfer through U-tubes, top plenum with the main steam system, downcomer (with feedwater injection) and natural circulation along the secondary loop included). But now replacing, among other essential improvements, the three characteristic channel elements of the code UTSG-2 (i.e. the primary and secondary side of the heat exchange zone and the riser) by adequate CCM modules.
The very successful application of the “separate-region coolant channel concept” within the code combination UTSG-3/CCM demonstrates the ability to find an exact and direct solution for the basic equations of a “non- homogeneous drift-flux based thermal-hydraulic mixture-fluid coolant channel model”. And it allows to check the performance and validity of the code package CCM and to verify it. For more details see [13] [31] [33] .
12. Verification and Validation (V & V) Procedures
During the course of development of the different versions of the code combination UTSG-3/CCM the module has gone through appropriate verification and validation (V & V) procedures (with continuous feedbacks being considered in the more and more advanced formulation of the theoretical model).
CCM is (similar as done in the separate-phase models) constructed with the objective to be used only as an element within an overall code. Hence, further V&V steps could be performed only in an indirect way, i.e. in combination with such overall codes. This has been achieved, as already explained in the section above, in a very successful way by means of the natural-circulation U-tube steam generator code UTSG-3. Thereby the module CCM could take advantage from the experiences been gained in decades of years work with the construction of an effective non-linear one-dimensional theoretical model and, based on it, corresponding digital code UTSG-2 for vertical, natural-circulation U-tube steam generators [9] - [11] [33] [34] [38] - [40] and now also the new advanced code version UTSG-3 [27] [28] .
The good agreement of the test calculations with similar calculations of earlier versions applied to the same transient cases demonstrates that despite of the continuous improvements of the code UTSG and the incorporation of CCM into UTSG-3 the newest and advanced version has still preserved its validity.
A more detailed description over these general V&V measures demonstrated on one characteristic test case can be found in [13] .
13. Conclusions
The universally applicable coolant channel module CCM has been established with the aim to describe the thermal-hydraulic situation of a coolant flowing up-, horizontal or downwards along any channel with fluids changing between sub-cooled, saturated, superheated and supercritical conditions. It must be recognized that it represents a complete system in its own right, which requires only BC-related, and thus easily available input values (geometry data, initial and boundary conditions, resulting parameters from integration). The partitioning of a basic channel into SC-s is done automatically within the module, requiring no special actions on the part of the user. At the end of a time-step, the characteristic parameters of all SC-s are transferred to the corresponding BC positions, thus yielding the final set of ODE-s together with the parameters following from the constitutive equations of CCM.
The resulting equations for different channels appearing in a complex physical system can be combined with other sets of algebraic equations and ODE-s coming from additional parts of such a complex model (heat transfer or nuclear kinetics considerations, top plenum, main steam system and downcomer of a steam generator etc.). The final overall set of ODE-s can then be solved by applying an appropriate time-integration routine [13] [27] [33] - [35] .
The enormous efforts already made in the verification and validation of the code UTSG-3, its application in a number of transient calculations at very extreme situations (fast opening of safety valves, dry out of the total channel with SC-s disappearing or created anew) brings the code and thus also CCM to a very mature and (what is important) easily applicable state.
There is, however, not yet enough experience to judge how the potential of the mixture -fluid models and especially of CCM can be expanded to other extreme cases (e.g., water and steam hammer). Is it justified to prefer separate-phase models versus the drift-flux based (and thus non-homogeneous) mixture fluid models? This depends, among other criteria, also on the quality of the special models and their exact derivation.
Considering the arguments presented above it can, however, be stated that in general the here presented “Separate-Region Mixture Fluid” concept offers a very satisfactory alternative to the currently dominant “Separate-Phase Model” concepts.
A very detailed derivation in this paper established set of characteristic model equations for both the polygon approximation procedure PAX (as a part of CCM) but also of the Coolant Channel Module CCM is given in [41] [42] .
Cite this paper
Alois Hoeld, (2015) A Thermal-Hydraulic Coolant Channel Module (CCM) for Single- and Two-Phase Flow. Applied Mathematics,06,2014-2044. doi: 10.4236/am.2015.612179
References
- 1. Liles, D.R., et al. (1988) TRAC-PF1/MOD1—Correlations and Models. NUREG/CR-5069, LA-11208-MS.
- 2. US-NRC (2001) TRAC-M / FORTRAN90. Version 3.0, Theory Manual, NUREG/CR-6724.
- 3. Hanna, B.N. (1998) CATENA. A Thermalhydraulic Code for CANDU Analysis. Nuclear Engineering and Design, 180, 113-131.
http://dx.doi.org/10.1016/S0029-5493(97)00294-X - 4. Shultz, R.R. (2003) RELAP5-3D Code Manual. Volume V: User’s Guidelines. INEEL-EXT-98-00084.
- 5. US-NRC (2001) RELAP5/ MOD3.3. Code Manual. NUREG/CR-5535.
- 6. Bestion, D. (1990) The Physical Closure Laws in CATHARE Code. Nuclear Engineering and Design, 124, 229-245.
http://dx.doi.org/10.1016/0029-5493(90)90294-8 - 7. Austregesilo, H., et al. (2003) ATHLET Mod 2.0, Cycle A, Models and Methods. GRS-P-1/Vol.4.
- 8. Lerchl, G., et al. (2009) ATHLET Mod 2.2, Cycle B, User’s Manual. GRS-P-1/Vol.1.
- 9. Hoeld, A. (1978) A Theoretical Model for the Calculation of Large Transients in Nuclear Natural Circulation U-Tube Steam Generators (Digital Code UTSG). Nuclear Engineering and Design, 47.
http://dx.doi.org/10.1016/0029-5493(78)90001-8 - 10. Hoeld, A. (1990) UTSG-2. A Theoretical Model Describing the Transient Behaviour of a PWR Natural-Circulation U-Tube Steam Generator. Nuclear Technology, 90, 98-118.
- 11. Hoeld, A. (1990) The Code ATHLET as a Valuable Tool for the Analysis of Transients with and without SCRAM. SCS Eastern MultiConference, Nashville, 23-26 April 1990.
- 12. Hoeld, A. (2011) Coolant Channel Module CCM. An Universally Applicable Thermal-Hydraulic Drift-Flux Based Separate-Region Mixture-Fluid Model. In: Uchanin, V., Ed., INTECH Open Access Book “Steam Generator Systems: Operational Reliability and Efficiency”, InTech, Austria.
http://www.intechopen.com/articles/show/title/the-thermal-hydraulic-u-tube-steam-generator-model-and-code-utsg-3-based-on-the-universally-applicable
http://www.intechopen.com/search?q=hoeld
http://dx.doi.org/10.5772/15979 - 13. Hoeld, A. (2011) The Thermal-Hydraulic U-Tube Steam Generator Model and Code UTSG3 (Based on the Universally Applicable Coolant Channel Module CCM). See INTECH Open Access Book Referred Above.
http://www.intechopen.com/search?q=hoeld
http://dx.doi.org/10.5772/15226 - 14. Hoeld, A. (2013) The Coolant Channel Module CCM—A Basic Element for the Construction of Thermal-Hydraulic Models and Codes. In: Guillen, D.P., Ed., INTECH Open Access Book “Nuclear Reactor Thermal Hydraulics and other Applications”, InTech, Croatia, 3-44.
http://www.intechopen.com/download/pdf/42936/
http://dx.doi.org/10.5772/53372 - 15. Hoeld, A. (1996) Thermodynamisches Stoffwertpaket MPP für Wasser und Dampf. GRS, Technische Notiz, TN-HOD-1/96, Mai.
- 16. Schmidt, E. and Grigull, U. (Ed.) (1982) Properties of Water and Steam in SI-Units. Springer-Verlag.
- 17. Haar, L., Gallagher, J.S., Kell, G.S. and Grigull, U. (1988) NBS/NRC Wasserdampftafeln. London/Paris/New York.
http://dx.doi.org/10.1007/978-3-642-52087-7 - 18. Moody, N.L.F. (1994) Friction Factors for Pipe Flow. Trans ASME, 66, 671. (See Also VDI-Wärmeatlas, 7 Auflage 1994,VDI-Verlag)
- 19. Martinelli, R.C. and Nelson, D.B. (1948) Prediction of Pressure Drop during Forced-Circulation of Boiling Water. Trans.ASME, 70, 695.
- 20. Sonnenburg, H.G. (1989) Full-Range Drift-Flux Model Based on the Combination of Drift-Flux Theory with Envelope Theory. NURETH-4, Karlsruhe, 10-13 October 1989, 1003-1009.
- 21. Hoeld, A., Jakubowska, E., Miro, J.E. and Sonnenburg, H.G. (1992) A Comparative Study on Slip and Drift-Flux Correlations. GRS-A-1879.
- 22. Hoeld, A. (2001) The Drift-Flux Correlation Package MDS. 9th International Conference on Nuclear Engineering (ICONE-9), Nice, 8-12 April 2001.
- 23. Hoeld, A. (2002) The Consideration of Entrainment in the Drift-Flux Correlation Package MDS. 10th International Conference on Nuclear Engineering (ICONE-10), Arlington, 14-18 April 2002.
http://dx.doi.org/10.1115/icone10-22692 - 24. Zuber, N. and Findlay, J.A. (1965) Average Volume Concentration in Two-Phase Flow Systems. Journal of Heat Transfer, 87, 453.
http://dx.doi.org/10.1115/1.3689137 - 25. Ishii, M. and Mishima, K. (1980) Study of Two-Fluid Model and Interfacial Area. NUREG/CR-1873 (ANL-80-111).
- 26. Ishii, M. (1990) Two-Fluid Model for Two-Phase Flow. Multiphase Sci. and Techn. 5.1, Hemisphere Publ. Corp.
- 27. Hoeld, A. (2004) A Theoretical Concept for a Thermal-Hydraulic 3D Parallel Channel Core Model. PHYSOR 2004, 25-29 April 2004, Chicago.
- 28. Jewer, S., Beeley, P.A., Thompson, A. and Hoeld, A. (2005) Initial Version of an Integrated Thermal-Hydraulic and Neutron Kinetics 3D Code X3D. ICONE13, 16-20 May 2005, Beijing. See also NED 236(2006), 1533-1546.
- 29. Hoeld, A. (1999) An Advanced Natural-Circulation U-Tube Steam Generator Model and Code UTSG-3. EUROTHERM-SEMINAR No. 63, 6-8 September 1999, Genoa.
- 30. Hoeld, A. (2002) A Steam Generator Code on the Basis of the General Coolant Channel Module CCM. PHYSOR 2002, 7-10 October 2002, Seoul.
- 31. Hoeld, A. (2000) The Module CCM for the Simulation of the Thermal-Hydraulic Situation within a Coolant Channel. International NSS/ENS Conference, Bled, 11-14 September 2000.
- 32. Hoeld, A. (2004) Are Separate-Phase Thermal-Hydraulic Models Better than Mixture-Fluid Approaches. It Depends. Rather Not. International Conference on Nuclear Engineering for New Europe, Portoroz, 6-9 September 2004.
- 33. Hoeld, A. (2005) A Thermal-Hydraulic Drift-Flux Based Mixture-Fluid Model for the Description of Single- and Two-Phase Flow along a General Coolant Channel. The 11th International Topical Meeting on Nuclear Reactor Thermal-Hydraulics (NURETH-11), Paper 144, Avignon, 2-6 October 2005.
- 34. Hoeld, A. (2007) Coolant Channel Module CCM. An Universally Applicable Thermal-Hydraulic Drift-Flux Based Mixture-Fluid 1D Model and Code. Nuclear Engineering and Design, 237, 1952-1967.
http://dx.doi.org/10.1016/j.nucengdes.2007.02.027 - 35. Hoeld, A. (2007) Application of the Mixture-Fluid Channel Element CCM within the U-Tube Steam Generator Code UTSG-3 for Transient Thermal-Hydraulic Calculations. 15th International Conference on Nuclear Engineering (ICONE-15), Paper 10206, Nagoya, April 22-26 2007.
- 36. Fabic, S. (1996) How Good Are Thermal-Hydraulics Codes for Analyses of Plant Transients. International ENS/HND Conference, Opatija, 7-9 October 1996, 193-201.
- 37. Hoeld, A. (1988) HETRAC: A Heat Transfer Coefficients Package. GRS-A-1446.
- 38. Hoeld, A. (1988) Calculation of the Time Behavior of PWR NPP during a Loss of a Feedwater ATWS Case. NUCSAFE 88, Avignon, 2-7 October 1988, 1037-1047.
- 39. Bencik, V. and Hoeld, A. (1991) Experiences in the Validation of Large Advanced Modular System Codes. SCS Simulation MultiConference, New Orleans, 1-5 April 1991.
- 40. Bencik, V. and Hoeld, A. (1993) Steam Collector and Main Steam System in a Multi-Loop PWR NPP Representation. Simulation MultiConference, Arlington, 29 March-1 April 1993.
- 41. Hoeld, A. (2015) Coolant Channel Module CCM (Detailed Derivation of the Characteristic Model Equations). Private Communication.
- 42. Hoeld, A. (2015) Quadratic Polygon Approximation Procedure PAX (Detailed Derivation of the Characteristic Model Equations). Private Communication.
Nomenclature
Subscripts
Superscripts
Acronyms






