Applied Mathematics
Vol.06 No.06(2015), Article ID:56860,8 pages
10.4236/am.2015.66088
Numerical Approximation of Quantum-Integrals Using the Appropriate Nodes and Weights
S. M. Hashemiparast1,2, D. A. Ghondaghsaz2, M. Maghasedi2
1School of Mathematics, KNT University of Technology, Tehran, Iran
2Department of Mathematics, College of Basic Sciences, Karaj branch Islamic Azad University, Alborz, Iran
Email: hashemiparast@kntu.ac.ir
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 April 2015; accepted 30 May 2015; published 2 June 2015
ABSTRACT
In this paper, we present a procedure for the numerical q-calculation of the q-integrals based on appropriate nodes and weights which are determined such that the error of q-integration is minimized; a system of linear and nonlinear set of equations respectively are prepared to obtain the nodes and weights simultaneously; the error of q-integration is considered to be minimized under this condition; finally some application and numerical examples are given for comparison with the exact solution. At the end, the related tables of approximations are presented.
Keywords:
q-Calculation, Numerical Approximation, q-Integration, q-Derivative

1. Introduction
Recently, much attention has been paid on q-calculus, especially on q-fractional calculus which finally most of them have changed to q-integral not easy and even possible to be solved analytically [1] . Although some series expansions have been developed for quantum integrals [2] and quantum differential equations and quantum difference equations [3] - [6] or q-fractional calculus [6] [7] , but because of small fractional power in the series expansion, one will expect a high degree of error in the truncated series [7] - [9] . The nominal numerical methods for approximating integrals do not seem to be appropriate for q-integrals. We could find less works for developing numerical procedures for accurate numerical solutions [9] - [14] . In this paper, we present a procedure for the numerical q-calculation of the q-integrals based on appropriate nodes and weights which are determined such that the error of q-integration is minimized. This study is organized such that in Section 2 we introduce the basic definitions and theorems related to the q-integrals; in Section 3, the main algorithm for the numerical approximation based on appropriate nodes and weights is introduced and the system of linear equations for the nodes and also nonlinear equations for the weights are established; in Section 4, numerical examples for illustration of the procedure are shown; finally, the related tables and graphs and conclusion are given.
2. Basic Definitions and Theorems
In this section we define the basic definitions and theorems related to the quantum integration
Jackson’s definition [15] for the q-integral is:
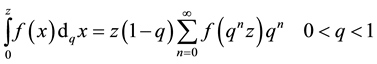 (1)
(1)
when 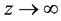
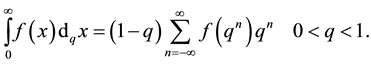 (2)
(2)
For the continuous function f in the interval [0, z] we have [8] :
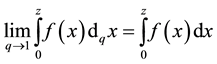 (3)
(3)
and
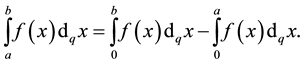 (4)
(4)
The generalized q-integral for 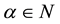 is defined as:
is defined as:
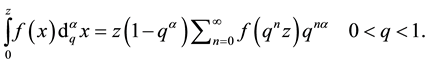 (5)
(5)
Similarly
 (6)
(6)
For the integer number n, the quantum integer is defined as a [n]q (bracket n) such that
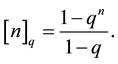 (7)
(7)
In [16] , for  q-derivative operator
q-derivative operator  is defined as:
is defined as:
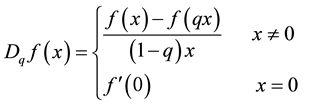 (8)
(8)
and the generalized q-derivative for 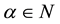 is defined as:
is defined as:
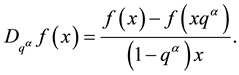 (9)
(9)
Similarly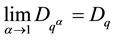 .
.
Analytical calculation of q-integrals similar to the ordinary integrals leads to extending these integrals as a series expansion, [10] applies q-taylor expansion, [17] introduces q-integrals inequalities and [16] takes advantage of hypergeometricpolynomials to express the q-integralas a series expansion, the inequalities in [17] help to find limit for q integrals, [12] generalizes the procedures of integral to some kind of q-integrals, and finally we generalize the procedure similar in [13] [18] .
3. Numerical Approximation of q-Integral
For a given value of q the following approximation can be established
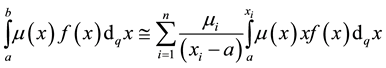 (10)
(10)
where



By calculating the limits in either side we get

Similar to the algorithm used in [5] we have the following theorem:
Theorem: The q-normal equations for 


Proof: Without losing the generality, for





Hence, we have the following system of equations

This can be summarized as the following matrix form such that for

where

is a Toeplitz matrix [10,11], whose entries are quantum numbers so, we call it quantum Toeplitz matrix, an especial form of n-diameter quantum matrix and keeps the non-singularity or singularity properties of the original matrix, because all elements of matrix have been changed simultaneously, positive Toplitz matrices, quantum matrices and Inversion of Toeplitz matrices are considered in [19] - [23] , so for having a unique solution, the same conditions for the original system of equations (q = 1) must be satisfied (12) for the different values of q, the elements of vector C and the nodes satisfy in the following characteristics equation [13]

Now, the roots of above characteristics equations are the appropriate nodes, satisfying in the system of simultaneous equations, then having these nodes the weighs μi can be evaluated, and by applying these values in (12) the system of Equation (13) will be obtained to evaluate the approximate values of the quantum integral, obviously the unknown in the system of equations depend upon the quantum parameter
In Section 3 we illustrate the algorithm for the numerical approximation of q-integral and some examples to illuminate the exactness of the method.
4. Algorithm for the Numerical Solution
We start the algorithm by the small values of n and similar method can be extended to any value of n, let n = 2, then for the evaluated values of xi s and μi

characteristic equation is

The system of equations is:


Then

different approximation can be expected for the different values of q, which for some values of q, 0 < q < 1, q-integral may have minimum error, if 




This gives

Then the characteristic equation is

Gives the following roots
By solving the linear system we obtain μ1, μ2

And the numerical q-integration formula for q = 0.1 can be evaluated from


Let n = 3, then for the evaluated values of xis and, xis

Characteristics equations is

For n = 3, the system of equations is


Similarly, for q = 0.1 numerical q-integration is

This gives

And a characteristics equation is:

With the roots as follows
Now, for calculating 

And we will have
Finally the numerical q-integration for q = 0.1 takes the following form

Tables 1-3 give the q-integral approximation for n = 2, 3, 4 respectively and some values of q.
Table 1. Give q-integral approximation for n = 2 and different values of q.
Table 2. Give the q-integral approximation for n = 3 and different values of q.
Table 3. Give the q-integral approximation for n = 4 and different values of q.
Table 4. Give the q-integral approximation for n = 2 and almost extreme value of q = 0.99999 for three different integrants in a specified interval.
5. Error Analysis and Application of q-Integral for Integral Approximation
The numerical values show for all values of n the error of q-integrations fluctuate for different values of q, it seems q = 0.70 gives the worse error almost for all values of n, the errors decreases as q approaches to the extreme values 0 and 1. Using this result and (3) the q-integral can be calculated for very large value of q approaching to 1 which will approximate the ordinary integrals whose q-integrals is easier than ordinary integrals by using q-integral approximation for n = 2 and different values of q, as illustrated in Table 4 and following the examples, where
6. Conclusion
In this paper, a new algorithm for the numerical approximation of q-integration based on q-calculation of appropriate nodes and weights is introduced. The evaluation of nodes and weight is based on q-integral error minimization, as expected in the numerical examples which give a good approximation in comparison with exact solutions for the given values of q and fixed n. As the q-fractional integration can be transferred to q-integrals, the procedure is also applicable for q-fractional integration, and also improper integrals for the large values of q.
References
- Rajkovic, P.M., Marinkovic, S.D. and Stankovic, M.S. (2007) Fractional Integrals and Derivatives in q-Calculus. Applicable Analysis and Discrete Mathematics, 1, 311-323. http://dx.doi.org/10.2298/AADM0701311R
- Bostan, A., Salvy, B., Chowdhury, M.F.I., Schost, E., Lebreton, R. and Max, E. (2014) Power Series Solution of Singular q-Differential Equations. Journal of Combinatorial Theory, Series A, 121, 45-63. http://dx.doi.org/10.1016/j.jcta.2013.09.005
- Kim, T. (2007) On the Analogs of Euler Number and Polynomials Associated with p-Adic q-Integral on Zp at q = −1. Journal of Mathematical Analysis and Applications, 331, 779-792. http://dx.doi.org/10.1016/j.jmaa.2006.09.027
- Lim, S.C., Eab, C.H., Mak, K.H., Li, M. and Chen, S.Y. (2012) Solving Linear Coupled Fractional Differential Equations by Direct Operational Method and Some Applications. Mathematical Problems in Engineering, 2012, Article ID: 653939. http://dx.doi.org/10.1155/2012/653939
- Foupouagnigni, M., Koepf, W. and Ronveaux, A. (2004) On Factorization and Solutions of q-Difference Equations Satisfied by Some Classes of Orthogonal Polynomials. Journal of Computational and Applied Mathematics, 162, 299- 326. http://dx.doi.org/10.1016/j.cam.2003.04.005
- Bowman, D. and Sohn, J. (1999) Partial q-Differences Equations for Basic Hypergeometric Function and Their q-Con- tinued Fractions. University of Illinois.
- De la Sen, M. (2014) On Nonnegative Solutions of Fractional q-Linear Time-Varying Dynamics. Hindawi Publisher Co. Abstract and Applied Analysis, 2014, Article ID: 247375. http://dx.doi.org/10.1155/2014/247375
- Simsek, Y. (2006) q-Dedekind Type Sums Related to q-Zeta Function and Basic L-Series. Journal of Mathematical Analysis and Applications, 318, 333-351. http://dx.doi.org/10.1016/j.jmaa.2005.06.007
- Abdeljavad, T., Benli, B. and Baleanu, D. (2012) A Generalized q-Mittag-Leffler Function by q-Captuo Fractional Linear Equations. Hindawi Publisher Co. Abstract and Applied Analysis, 2012, Article ID: 546062.
- Ismail, M.E.H. and Stanton, D. (2003) q-Taylor Theorems, Polynomial Expansions and Interpolation of Entire Functions. Journal of Approximation Theory, 123, 125-146. http://dx.doi.org/10.1016/S0021-9045(03)00076-5
- Stankovic, M.S., Rajkovic, P.M. and Marinkovic, S.D. (2006) Inequalities Which Includes q-Integrals. Bulletin: Classe des sciences mathematiques et natturalles, 133, 137-146.
- Wu, G.-C. and Baleanu, D. (2013) New Application of the Variation Iteration Method from Differential Equation to q-Fractional Difference Equations. Advanced in Difference Equation, 21.
- Hashemiparast, S.M. (2011) Numerical Solution of the Integrals by Using Appropriate Nodes and Weights. Proceedings of the ICMS Conference, Istanbul.
- Ernst, T. (2003) A Method for q-Calculus. Journal of Nonlinear Mathematical Physics, 10, 487-525. http://dx.doi.org/10.2991/jnmp.2003.10.4.5
- Jackson, F.H. (1910) On q-Definite Integrals. Quarterly Journal of Pure and Applied Mathematics, 41, 193-203.
- Koekoek, R., Alesky, P. and Swarrouw, R. (2010) Hyper Geometric Orthogonal Polynomials and Their q-Analogues. Cambridge University Press, Cambridge.
- Miao, Y. and Feng, Q. (2009) Several q-Integrals Inequalities. Journal of Mathematical Inequalities, 3, 115-121. http://dx.doi.org/10.7153/jmi-03-11
- Hashemiparast, S.M., Eslahchi, M.R. and Dehghan, M. (2007) Determination of Nodes in Numerical Integration Rules Using Difference Equations. Applied Mathematics and Computation, 176, 117-122.
- Rietsch, K. (2001) Totally Positive Toeplitz Matrices and Quantum Cohomology of Partial Flag Varieties. Journal of the American Mathematics Society, 16, 363-392.
- Andersen, J.E. and Berg, C. (2009) Quantum Hilbert Matrices and Orthogonal Polynomials. Journal of Computational and Applied Mathematics, 233, 723-729.
- Cooper, A.P. (2011) The Quantum Matrix. The Author and Copyrights ©2011.
- Gray, R.M. (2006) Toeplitz and Circulant Matrices: A Review. Department of Electrical Engineering, Stanford University, Stanford.
- Lv, X.-G. and Huang, T.-Z. (2007) A Note on Inversion of Toeplitz Matrices. Applied Mathematics Letters, 20, 1189- 1193. http://dx.doi.org/10.1016/j.aml.2006.10.008








