Applied Mathematics
Vol.06 No.03(2015), Article ID:54568,10 pages
10.4236/am.2015.63048
An Improved Approach of Surface Meshes
Bashar Zogheib, Ali El Saheli
Department of Mathematics and Natural Sciences, American University of Kuwait, Salmiya, Kuwait
Email: bzogheib@auk.edu.kw, aelsaheli@auk.edu.kw
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 February 2015; accepted 10 March 2015; published 11 March 2015
ABSTRACT
In this paper, various grid generation techniques are described, and the importance of control functions in elliptic grid generation is discussed. In particular, a new form of the control functions is proposed for surface mesh generation, based on successful representation for planar mesh ge- neration developed by [1] . These control functions are designed to enhance orthogonality of the mesh near the boundaries. Three examples are set up to illustrate the advantages of the proposed method. For each example, surface meshes are generated using several other well-established me- thods, including transfinite interpolation and elliptic differential equation systems. These methods can create meshes of reasonably good quality, but when compared to each other, the pre- sent method is the best one for giving very good quality meshes.
Keywords:
Mesh Generation, Surface, Grids, Quality, Boundaries

1. Introduction
Surface modeling and grid generation technologies have been long recognized as critical issues in practical applications of computational fluid dynamics [2] . For this reason tools have been developed to implement these geometry modeling technologies in a reasonably versatile and efficient manner.
Surface modeling and grid generation technologies, of course, do not produce a complete design. They are components of a complex design process. Surface grid generation is a time consuming step in the overall process. Surface models and grids are of value only so far as they allow high quality flow predictions to be made at an acceptable cost. The quality of the surface grid has a great impact on the overall quality of the final analysis product.
Researchers have shown that many methods do not ensure that the final surface grid points lie exactly on the original defined surface. It is at present very difficult to assess surface grid quality (orthogonality, curvature, stretching) by any means other than visual inspection. Inspection, of course, is not a systematic process. Further, there are very few absolute measures of quality. This approach leaves a high probability that defects will not be detected at the surface meshing stage, and they will remain in the surface grid to have a magnified impact in later steps of the process. Several methods have been constructed for the generation of good quality meshes on surfaces. The method of [1] for planar coordinates can be extended for surface meshing, as seen in this paper. In his paper, [3] proposed a method which is based on the construction of a continuously differentiable surface from a given control point set and on the algebraic generation of a mesh on this surface by mapping of a mesh in a parametric space. In his article, [4] developed a set of second order differential equations for the generation of coordinates in a given surface and then solved numerically to demonstrate its potential for surface coordinate generation. In their paper, [5] described a procedure for generating curved meshes, suitable for high-order finite element analysis. The strategy they adopted is based upon curving a generated initial mesh with planar edges and faces by using a linear elasticity analogy. The analogy employs boundary loads that ensure that nodes re- presenting curved boundaries lie on the true surface. They used several examples, to illustrate the performance of the proposed approach, and the quality of the generated meshes was analyzed in terms of a distortion measure. In their paper, [6] presented an automatic 3D method for constructing unstructured tetrahedral and hexahedral meshes for a composite domain made up of heterogeneous materials, where the boundaries of these material regions form non-manifold surfaces. An overview of surface and volume mesh generation techniques for creating valid meshes to carry out biomedical flows was provided by [7] . Applications discussed were hemodynamic in blood vessels and air flow in upper human respiratory tract. The described semi-automatic methods were designed to minimize distortion to a given domain boundary and to generate a triangular surface mesh first and then volume mesh (tetrahedrons) with high quality surface and volume elements. A new method for anisotropic surface meshing which generates a curvature-adapted mesh was created by [8] . The main idea of their work consists in transforming the 3d anisotropic space into a higher-dimensional isotropic space (typically 6d or larger). In this high dimensional space, the mesh is optimized by computing a Centroidal Voronoi Tessellation, the minimizer of a C2 objective function that depends on the coordinates at the vertices. They demonstrated their method with several examples comprising CAD and scanned meshes. A method to optimize triangular and quadrilateral meshes on parameterized surfaces was proposed by [9] . The optimization procedure presented by the authors relocates the nodes on the surface to improve the quality (smooth) and ensures that the elements are not inverted (untangle). This method was proved to be independent of the surface parameterization, and, therefore, it can optimize meshes on CAD surfaces defined by low-quality parameterizations.
In this paper, a new approach to create surface meshes is developed. This approach is based on [1] for planar grids. Three examples of different meshes are provided to show the quality of the proposed approach compared to some of the well known methods.
2. Surface Grid Generation Equations
Method of [1] for planar systems will be followed to derive the equations for surface grid generation and to evaluate the control functions 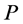 and
and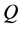 . If the surface itself is specified by
. If the surface itself is specified by 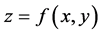 this surface then corresponds to one of the curvilinear coordinates (in 3D) being constant. Thus the curved surface can be mapped to a plane rectangular region, where the curves which bound the surface are mapped to straight boundaries in the computational space. Hence the problem is essentially the same as for 2D plane regions, the only difference being that the curvature of the surface will enter the generation equation.
this surface then corresponds to one of the curvilinear coordinates (in 3D) being constant. Thus the curved surface can be mapped to a plane rectangular region, where the curves which bound the surface are mapped to straight boundaries in the computational space. Hence the problem is essentially the same as for 2D plane regions, the only difference being that the curvature of the surface will enter the generation equation.
Using the notation of [10] of the 2D planar formulation, an elliptic grid on a surface can be generated from the system
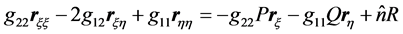 (1)
(1)
where 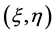 are coordinates on the surface
are coordinates on the surface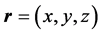 ,
, 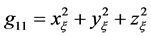 ,
, 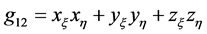 ,
, 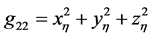 ,
,  is the unit normal to the surface and
is the unit normal to the surface and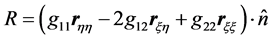 .
.
The control functions 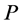 and
and 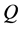 will be derived following the ideas of [1] [11] . Imposing the condition of orthogonality along the boundary curve
will be derived following the ideas of [1] [11] . Imposing the condition of orthogonality along the boundary curve  and taking the dot product of the grid generation Equations (1) with
and taking the dot product of the grid generation Equations (1) with , Equation (2) is obtained
, Equation (2) is obtained
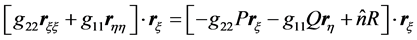 (2)
(2)
Given that
And since


Similarly if the dot product of Equation (1) with 

Equation (4) is obtained

Since 






With the assumption of orthogonality on the boundaries, it is known that

With the additional assumption of orthogonality in a thin layer of cells near the boundary, say



Since the spacing 



the analogous expression for 
3. Quality of Meshes
Orthogonality is one of the important features that determine the quality of a mesh. In many cases the aim is not really to produce a completely orthogonal grid, but rather to achieve near orthogonality throughout the region and true orthogonality at the boundaries. Several procedures can be used to check for orthogonality. The ones used in this paper are orthogonality functionals and area-orthogonality functionals. In their paper, [12] discuss these and other functionals which, when minimized, lead to various grid generation systems.
Recall that exact orthogonality at all grid points means that 

it can be shown [5] that the Euler-Lagrange equations for this functional are nonelliptic equations which often fail to generate a grid. Nevertheless, the minimum value of this functional can be viewed as a measure of orthogonality.
A second orthogonality functional is 
two tangent vectors and not their lengths. This functional is considered to be a good grid generator. In these two integrals, if the mesh is exactly orthogonal, then 



proportional to some given weight function. By taking a linear combination of area and orthogonality functionals, grid generators which simultaneously try to enforce equidistributed cell areas and orthogonality can be obtained. The name AO derives from the fact that the functional is halfway between the equal area and orthogonal-
ity functional. Two such functionals to be minimized are 
Another type of functional, with a guaranteed unique minimum, was proposed by Liao. The Modified Liao functional, designed to reduce the tendency for the grids to fold, is

For our purpose, we will evaluate these functionals for the grids generated by the above methods, and look for the method which produces the minimum value.
4. Examples
Three surface grids are created using the present method, method created by [11] , Laplace equations and algebraic methods. These examples are chosen in a way that surface grid features like orthogonality, smoothness, curvature, can be checked easily.
4.1. Example 1
In this example a mesh on a paraboloid surface with equation 





Figure 1. Algebraic method.
Figure 2. Laplace equations.
Figure 3. Present method.
Figure 4. Thomas’s & Middlecoff’s method.
Table 1. Mesh quality.
4.2. Example 2
In this example the paraboloid given in Example 1 is modified and a mesh is generated using the polynomial 

plane. The other three boundary curves are kept the same. The quality of the mesh and the number of iterations used by each method are shown in Table 2, and the meshes are shown in Figures 5-8.
From Table 2 it is clear that, among the elliptic methods, the present method gives the best mesh only in the sense of area-orthogonality squared while Thomas and Middlecoff does better on a strictly orthogonality criterion. Algebraic method gives the worst mesh in the sense of orthogonality. The tendency of the present method to equally distribute the cell areas can be seen from Figure 5, particularly near the right hand boundary.
4.3. Example 3
In this example the paraboloid given in Example 1 is modified and a mesh is generated using the intersection of two planes with the paraboloid to replace the circle 

where 


kept the same. The quality of the mesh and the number of iterations used by each method are shown in Table 3, and the meshes are shown in Figures 9-12.
From Table 3 it is clear that the present method is the best in the sense of orthogonality on all measures, while the Laplace system converges in less number of iterations than the other methods. Thomas and Middlecoff and the Laplace system are about the same in providing an orthogonal mesh. The algebraic method gives the worst mesh in the sense of orthogonality. Even though only the algebraic method gives grid points in the cusp
region near
a flow solver. To properly mesh the cusp region using these differential equations methods, multiblock approach can be used, drawing a block boundary curve from the cusp and distributing points along this curve.
5. Conclusions
A mesh can be generated using many methods. The methods used in this paper are algebraic methods, Laplace equations, Thomas and Middlecoff’s method and the extension of Barron’s method from planar regions to surfaces. To generate a rough mesh, algebraic method is the easiest to use because it creates a mesh in one iteration only. To create a smooth mesh one can use Laplace equations. Thomas and Middlecoff method can be used to obtain a good mesh in the sense of orthogonality and the number of iterations, but the best method to obtain a
Figure 5. Algebraic method.
Figure 6. Laplace equations.
Figure 7. Present method.
Figure 8. Thomas’s & Middlecoff’s method.
Figure 9. Algebraic method.
Figure 10. Laplace equations.
Figure 11. Present method.
Figure 12. Thomas’s & Middlecoff’s method.
Table 2. Mesh quality.
Table 3. Mesh quality.
more orthogonal mesh is the present method. The number of iterations for this method to converge is almost the same as that of Thomas and Middlecoff’s method.
Cite this paper
Bashar Zogheib,Ali El Saheli, (2015) Retraction: An Improved Approach of Surface Meshes. Applied Mathematics,06,510-519. doi: 10.4236/am.2015.63048
References
- 1. Barron, R. (1996) Improvements to Grid Quality and Cost of Multiblock Structured Grid Generation. Proceedings of CFD 96, 4th Annual Conference of CFD Society of Canada, CFD, Ottawa, 2-4 June 1996, 303-309.
- 2. NASA Conference Publications (1995) Surface Modeling, Grid Generation, and Related Issues in Computational Fluid Dynamic (CFD) Solutions. NASA CP 3291. NASA Lewis Research Center, Cleveland.
- 3. Desbois, F. and Jacquotte, O.O. (1991) Surface Mesh Generation and Optimization. In: Thompson, J.F., Ed., Numerical Grid Generation, North-Holland, 131-141.
- 4. Warsi, Z.U.A. (1986) Numerical Grid Generation in Arbitrary Surfaces through a Second-Order Differential-Geometric Model. Journal of Computational Physics, 64, 82-96.
http://dx.doi.org/10.1016/0021-9991(86)90019-7 - 5. Xie, Z.Q., Sevilla, R., Hassan, O. and Morgan, K. (2013) The Generation of Arbitrary Order Curved Meshes for 3D Finite Element Analysis. Computational Mechanics, 51, 361-374.
http://dx.doi.org/10.1007/s00466-012-0736-4 - 6. Zhang, Y., Hughesb, T.J.R. and Bajajc, C.L. (2010) An Automatic 3D Mesh Generation Method for Domains with Multiple Materials. Computer Methods in Applied Mechanics and Engineering, 199, 405-415.
http://dx.doi.org/10.1016/j.cma.2009.06.007 - 7. Sazonov, I. and Nithiarasu, P. (2012) Semi-Automatic Surface and Volume Mesh Generation for Subject-Specific Bio-medical Geometries. International Journal for Numerical Methods in Biomedical Engineering, 28, 133-157.
http://dx.doi.org/10.1002/cnm.1470 - 8. Levy, B. and Bonneel, N. (2013) Variational Anisotropic Surface Meshing with Voronoi Parallel Linear Enumeration. Proceedings of the 21st International Meshing Roundtable, Springer Berlin Heidelberg, Berlin, 349-366.
http://dx.doi.org/10.1007/978-3-642-33573-0_21 - 9. Gargallo-Peiró, A., Roca, X. and Sarrate, J. (2014) A Surface Mesh Smoothing and Untangling Method Independent of the CAD Parameterization. Computational Mechanics, 53, 587-609.
http://dx.doi.org/10.1007/s00466-013-0920-1 - 10. Thompson, J.F., Thames, F.C. and Mastin, C.W. (1974) Automatic Numerical Generation of Body-Fitted Curvilinear Co-ordinate System for Fields Containing Any Number of Arbitrary Two-Dimensional Bodies. Journal of Computational Physics, 15, 299-319.
http://dx.doi.org/10.1016/0021-9991(74)90114-4 - 11. Thomas, P. and Middlecoff, J. (1980) Direct Control of the Grid Point Distribution in Meshes Generated by Elliptic Equations. AIAA, 18, 652-656.
http://dx.doi.org/10.2514/3.50801 - 12. Knupp, P. and Steinberg, S. (1994) Fundamentals of Grid Generation. CRC Press, Boca Raton.

















