Applied Mathematics
Vol.06 No.02(2015), Article ID:53836,8 pages
10.4236/am.2015.62027
Thermal Radiation Effects on MHD Boundary Layer Flow over an Exponentially Stretching Surface
Santosh Chaudhary1, Sawai Singh2, Susheela Chaudhary2
1Department of Mathematics, Malaviya National Institute of Technology, Jaipur, Rajasthan, India
2Department of Mathematics, S. K. Govt. (P.G.) College, Sikar, Rajasthan, India
Email: d11.santosh@yahoo.com, dhayal.sawaisingh@yahoo.com, susheelamaths@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 January 2015; accepted 29 January 2015; published 5 February 2015
ABSTRACT
The steady two-dimensional laminar boundary layer flow and heat transfer of a viscous incompressible electrically conducting fluid over an exponentially stretching surface in the presence of a uniform magnetic field with thermal radiation are investigated. The governing boundary layer equations are transformed to ordinary differential equations by taking suitable similarity transformation and solved numerically by shooting method. The effects of various parameters such as magnetic parameter, radiation parameter, Prandtl number and Eckert number on local skin-fric- tion coefficient, local Nusselt number, velocity and temperature distributions are computed and represented graphically.
Keywords:
Thermal Radiation, MHD, Boundary Layer Flow, Exponentially Stretching Surface

1. Introduction
The study of boundary layer flow and its applications are vital for advancement in the field of technology and engineering. The computation and computer coordinated applications of flow over a stretching surface are playing a pivotal role in different realm of industrial products of aerodynamics, polymers and metallurgy, such as liquid films in condensation process, artificial fibers, glass fiber, metal spinning, the cooling process of metallic plate in a cooling bath and glass, wire drawing, paper production, aerodynamic extrusion of plastic sheets, crystal growing, cable coating and many others, to get end product of desired quality and parameters. Sakiadis [1] probably was the first who investigated boundary layer flow on a moving continuous solid surface. Crane [2] extended this concept to a linearly stretching plate whose velocity is linearly proportional to the distance from the slit and produced an exact analytical solution for the steady two-dimensional flow problems. Gupta and Gupta [3] , Carragher and Crane [4] , Grubka and Bobba [5] , Chen and Char [6] , Ali [7] , Andersson [8] , Ariel et al. [9] , Ishak et al. [10] , Jat and Chaudhary [11] [12] , Wang [13] and Nadeem et al. [14] analyzed the effects of heat transfer on a stretching surface taking into account different aspects of the problem.
Boundary layer flow and heat transfer over an exponentially stretching surface have wider applications in technology such as in case of annealing and thinning of copper wires. Magyari and Keller [15] obtained analytical and numerical solutions for boundary layer flow over an exponentially stretching continuous surface with an exponential temperature distribution. Many other problems on exponentially stretching surface under different physical situations were observed by Elbashbeshy [16] , Partha et al. [17] , Khan [18] , Sanjayanand and Khan [19] and El-Aziz [20] .
At higher operating temperature, the effects of thermal radiation and heat transfer play a pivotal role on the fluid flow problem of boundary layer. The application of controlled heat transfer in polymer industries is very important to get final product of desired parameters. The modern system of electric power generation, plasma, space vehicles, astrophysical flows and cooling of nuclear reactors are governed by applications of thermal radiation and heat transfer of fluid flow. Elbashbeshy [21] determined the effect of radiation on flow of an incompressible fluid along a heated horizontal stretching sheet. Sajid and Hayat [22] extended this concept by investigating the influence of thermal radiation on the boundary layer flow over an exponentially stretching sheet and solved the problem analytically. Recently, Bidin and Nazar [23] , Jat and Chaudhary [24] , Nadeem et al. [25] and Mukhopadhyay and Gorla [26] investigated various aspects of such problem either analytically or numerically.
With reference to above significant studies and in view of importance of MHD applications in various field of technologies, the objective of present paper is to investigate the effect of thermal radiation on an electrically conducting two-dimensional boundary layer incompressible viscous fluid flow over an exponentially stretching surface in the presence of uniform magnetic field by using Rosseland approximation. Numerical results of the momentum and energy equations are computed by using shooting method. The promising results of velocity and temperature distributions, local skin-friction coefficient and surface heat transfer are discussed for various physical parameters and simplified their effects for different conditions.
2. Problem Formulation
Consider the steady two-dimensional laminar boundary layer flow 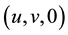 of a viscous incompressible electrically conducting radiative fluid over continuous exponentially stretching surface in the presence of an externally applied normal magnetic field of constant strength
of a viscous incompressible electrically conducting radiative fluid over continuous exponentially stretching surface in the presence of an externally applied normal magnetic field of constant strength . The x-axis is taken along the stretching surface in the direction of motion and y-axis is taken perpendicular to it. The stretching surface has a uniform temperature
. The x-axis is taken along the stretching surface in the direction of motion and y-axis is taken perpendicular to it. The stretching surface has a uniform temperature 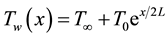 and a linear velocity
and a linear velocity  while temperature of flow external to the boundary layer is
while temperature of flow external to the boundary layer is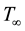 . The system of governing boundary layer equations (which model Figure 1) are given by:
. The system of governing boundary layer equations (which model Figure 1) are given by:
Figure 1. Sketch of the physical problem.
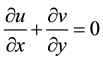 (1)
(1)
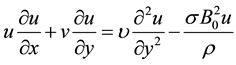 (2)
(2)
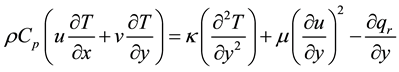 (3)
(3)
where T0 is the reference temperature, L is the reference length, U0 is the reference velocity,  is the coef-
is the coef-
ficient of kinematic viscosity,  is the coefficient of viscosity,
is the coefficient of viscosity, 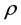 is the fluid density,
is the fluid density, 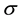 is the electrical conductivity, Cp is the specific heat at constant pressure, T is the temperature,
is the electrical conductivity, Cp is the specific heat at constant pressure, T is the temperature, 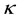 is the thermal conductivity and qr is the radiative heat flux. The other symbols have their usual meanings.
is the thermal conductivity and qr is the radiative heat flux. The other symbols have their usual meanings.
The boundary conditions are:
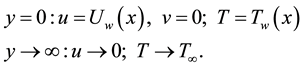 (4)
(4)
By using Rosseland approximation of the radiation for an optically thick boundary layer, the radiative heat flux qr is expressed (Bidin and Nazar [23] ) as:
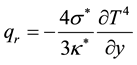 (5)
(5)
where 



Using Equation (5) and (6), equation (3) is reduced to:

3. Similarity Analysis
The continuity Equation (1) is identically satisfied if we defined stream function 

For the solution of momentum and energy Equations (2) and (7), introducing the following dimensionless variables:



Using Equations (8) to (11), Equations (2) and (7) are reduced to:


The boundary conditions are:

where prime (') denote differentiation with respect to η, 



4. Numerical Solution of the Problem
For numerical solution of the Equations (12) and (13), we use the following power series in terms of small magnetic parameter M as:


Substituting the values of 







The corresponding boundary conditions are:

The Equation (17) is same as that obtained by Bidin and Nazar [23] for non-magnetic case and the remaining equations from (18) to (22) are ordinary linear differential equations and have been solved numerically by Shooting method with boundary condition (23). The velocity and temperature distributions for various values of parameters are shown in Figures 2-6 respectively.
5. Local Skin Friction Coefficient and Local Nusselt Number
The important physical quantities are the local skin-friction coefficient Cf and the local Nusselt number Nu, which are defined as:
Figure 2. Velocity distribution against η for various values of M.
Figure 3. Temperature distribution against η for various values of M with K = 0.5, Pr = 1 and Ec = 0.0.
Figure 4. Temperature distribution against η for various values of K with M = 0.04, Pr = 1 and Ec = 0.0.
Figure 5. Temperature distribution against η for various values of Pr with M = 0.04, K = 0.5 and Ec = 0.0.
Figure 6. Temperature distribution against η for various values of Ec with M = 0.04, K = 0.5 and Pr = 1.

and

In the present case which can be expressed in dimensionless form as:

and

where 

values of 

6. Results and Discussion
Figure 2 shows variation of velocity distribution 

Figures 3-6 show the temperature distributions 


The values of the local skin-friction coefficient Cf and the local Nusselt number Nu in terms of 





Table 1. Variation of surface shear stress f'' (0) with M and surface heat transfer rate θ' (0) with M, K, Pr and Ec = 0.0.
7. Conclusion
The characteristic relationships among various parameters influencing viscous incompressible electrically conducting fluid over an exponentially stretching surface in the presence of a uniform magnetic field with thermal radiation have been analyzed and illustrated graphically. The similarity equations are determined and solved numerically by shooting method. It is observed that thickness of the velocity boundary layer, the local skin-friction coefficient and the local Nusselt number decreases with increasing value of the magnetic parameter. However, thickness of the thermal boundary layer increases with increasing value of the magnetic parameter. Further, it is observed that thickness of thermal boundary layer increases with increasing value of the radiation parameter or the Eckert number, whereas, reverse phenomenon observed for the Prandtl number. Moreover, the local Nusselt number decreases with increasing value of the radiation parameter, while reverse behaviour observed for the Prandtl number.
References
- Sakiadis, B.C. (1961) Boundary-Layer Behavior on Continuous Solid Surfaces: I. Boundary-Layer Equations for Two-Dimensional and Axisymmetric Flow. American Institute of Chemical Engineers Journal, 7, 26-28. http://dx.doi.org/10.1002/aic.690070108
- Crane, L.J. (1970) Flow past a Stretching Plate. Zeitschrift für Angewandte Mathematik und Physik, 21, 645-647. http://dx.doi.org/10.1007/BF01587695
- Gupta, P.S. and Gupta, A.S. (1977) Heat and Mass Transfer on a Stretching Sheet with Suction or Blowing. The Canadian Journal of Chemical Engineering, 55, 744-746. http://dx.doi.org/10.1002/cjce.5450550619
- Carragher, P. and Crane, L.J. (1982) Heat Transfer on a Continuous Stretching Sheet. Zeitschrift für AngewandteMathematik und Mechanik, 62, 564-565. http://dx.doi.org/10.1002/zamm.19820621009
- Grubka, L.J. and Bobba, K.M. (1985) Heat Transfer Characteristics of a Continuous, Stretching Surface with Variable Temperature. Journal of Heat Transfer, 107, 248-250. http://dx.doi.org/10.1115/1.3247387
- Chen, C.K. and Char, M.I. (1988) Heat Transfer of a Continuous, Stretching Surface with Suction or Blowing. Journal of Mathematical Analysis and Applications, 135, 568-580. http://dx.doi.org/10.1016/0022-247X(88)90172-2
- Ali, M.E. (1994) Heat Transfer Characteristics of a Continuous Stretching Surface. Heat and Mass Transfer, 29, 227- 234.
- Andersson, H.I. (2002) Slip Flow past a Stretching Surface. Acta Mechanica, 158, 121-125. http://dx.doi.org/10.1007/BF01463174
- Ariel, P.D., Hayat, T. and Asghar, S. (2006) The Flow of an Elastico-Viscous Fluid past a Stretching Sheet with Partial Slip. Acta Mechanica, 187, 29-35. http://dx.doi.org/10.1007/s00707-006-0370-3
- Ishak, A., Nazar, R. and Pop, I. (2006) Mixed Convection Boundary Layers in the Stagnation-Point Flow toward a Stretching Vertical Sheet. Meccanica, 41, 509-518. http://dx.doi.org/10.1007/s11012-006-0009-4
- Jat, R.N. and Chaudhary, S. (2008) Magnetohydrodynamic Boundary Layer Flow Near the Stagnation Point of a Stre- tching Sheet. Il Nuovo Cimento della Società Italiana di Fisica B: General Physics, 123, 555-566.
- Jat, R.N. and Chaudhary, S. (2009) MHD Flow and Heat Transfer over a Stretching Sheet. Applied Mathematical Sciences, 3, 1285-1294.
- Wang, C.Y. (2009) Analysis of Viscous Flow Due to a Stretching Sheet with Surface Slip and Suction. Nonlinear Analysis: Real World Applications, 10, 375-380. http://dx.doi.org/10.1016/j.nonrwa.2007.09.013
- Nadeem, S., Hussain, A. and Khan, M. (2010) HAM Solutions for Boundary Layer Flow in the Region of the Stagnation Point towards a Stretching Sheet. Communications in Nonlinear Science and Numerical Simulation, 15, 475-481. http://dx.doi.org/10.1016/j.cnsns.2009.04.037
- Magyari, E. and Keller, B. (1999) Heat and Mass Transfer in the Boundary Layers on an Exponentially Stretching Continuous Surface. Journal of Physics D: Applied Physics, 32, 577-585. http://dx.doi.org/10.1088/0022-3727/32/5/012
- Elbashbeshy, E.M.A. (2001) Heat Transfer over an Exponentially Stretching Continuous Surface with Suction. Archives of Mechanics, 53, 643-651.
- Partha, M.K., Murthy, P.V.S.N. and Rajasekhar, G.P. (2005) Effect of Viscous Dissipation on the Mixed Convection Heat Transfer from an Exponentially Stretching Surface. Heat and Mass Transfer, 41, 360-366. http://dx.doi.org/10.1007/s00231-004-0552-2
- Khan, S.K. (2006) Boundary Layer Viscoelastic Fluid Flow over an Exponentially Stretching Sheet. International Journal of Applied Mechanics and Engineering, 11, 321-335.
- Sanjayanand, E. and Khan, S.K. (2006) On Heat and Mass Transfer in a Viscoelastic Boundary Layer Flow over an Exponentially Stretching Sheet. International Journal of Thermal Sciences, 45, 819-828. http://dx.doi.org/10.1016/j.ijthermalsci.2005.11.002
- El-Aziz, M.A. (2009) Viscous Dissipation Effect on Mixed Convection Flow of a Micropolar Fluid over an Exponentially Stretching Sheet. Canadian Journal of Physics, 87, 359-368. http://dx.doi.org/10.1139/P09-047
- Elbashbeshy, E.M.A. (2000) Radiation Effect on Heat Transfer over a Stretching Surface. Canadian Journal of Physics, 78, 1107-1112. http://dx.doi.org/10.1139/p00-085
- Sajid, M. and Hayat, T. (2008) Influence of Thermal Radiation on the Boundary Layer Flow Due to an Exponentially Stretching Sheet. International Communications in Heat and Mass Transfer, 35, 347-356. http://dx.doi.org/10.1016/j.icheatmasstransfer.2007.08.006
- Bidin, B. and Nazar, R. (2009) Numerical Solution of the Boundary Layer Flow over an Exponentially Stretching Sheet with Thermal Radiation. European Journal of Scientific Research, 33, 710-717.
- Jat, R.N. and Chaudhary, S. (2010) Radiation Effects on the MHD Flow Near the Stagnation Point of a Stretching Sheet. Zeitschrift für angewandte Mathematik und Physik, 61, 1151-1154. http://dx.doi.org/10.1007/s00033-010-0072-5
- Nadeem, S., Zaheer, S. and Fang, T. (2011) Effects of Thermal Radiation on the Boundary Layer Flow of a Jeffrey Fluid over an Exponentially Stretching Surface. Numerical Algorithms, 57, 187-205. http://dx.doi.org/10.1007/s11075-010-9423-8
- Mukhopadhyay, S. and Gorla, R.S.R. (2012) Effects of Partial Slip on Boundary Layer Flow past a Permeable Exponential Stretching Sheet in Presence of Thermal Radiation. Heat and Mass Transfer, 48, 1773-1781. http://dx.doi.org/10.1007/s00231-012-1024-8








