Received 24 October 2014; revised 20 November 2014; accepted 16 December 2014

ABSTRACT

In the present paper we derived, with direct method, the exact expressions for the sampling probability density function of the Gini concentration ratio for samples from a uniform population of size n = 6, 7, 8, 9 and 10. Moreover, we found some regularities of such distributions valid for any sample size.

Keywords:

Gini Concentration Ratio, Uniform Distribution, Order Statistics, Probability Density Function

1. Introduction

In 1914 Corrado Gini [1] introduced the concentration ratio R for the measure of inequality among values of a frequency distribution. The Gini index is widely used in fields as diverse as sociology, health science, engineering, and in particular, economics to measure the inequality of income distribution.

Various aspects of the Gini index have been taken into account. One of the most interesting topics regards the estimation of the concentration ratio (Hoeffding, 1948 [2] ; Glasser, 1962 [3] ; Cucconi, 1965 [4] ; Dall’Aglio, 1965 [5] ). More recently, Deltas (2003) [6] discussed the sources of bias of the Gini coefficient for small samples. This has implications for the comparison of inequality among subsamples, some of which may be small, and the use of the Gini index in measuring firm size inequality in markets with a small number of firms. Barret and Donald (2009) [7] considered statistical inference for consistent estimators of generalized Gini indices. The empirical indices are shown to be asymptotically normally distributed using functional limit theory. Moreover, asymptotic variance expressions are obtained using influence functions. Davidson (2009) [8] derived an approximation for the estimator of the Gini index by which it is expressed as a sum of IID random variables. This approximation allows developing a reliable standard error that is simple to compute. Fakoor, Ghalibaf and Azarnoosh (2011) [9] considered nonparametric estimators of the Gini index based on a sample from length-bi- ased distributions. They showed that these estimators are strongly consistent for the Gini index. Also, they obtained an asymptotic normality for the corresponding Gini index.

Girone (1968) [10] focused on the study of the sampling distribution of the Gini index and in 1971 [11] derived the exact expression for samples drawn from an exponential population. In 1971 Girone [12] obtained, with direct method, the sampling distribution function of the Gini ratio for samples of size n ≤ 5 drawn from a uniform population.

In the present note (Section 2), we calculate the joint probability density function (p.d.f.) of the random sample of size n and, then, the joint p.d.f. of the n order statistics. Hence, we transform one of the order statistics in their average and the remaining n ‒ 1 order statistics are divided by the same average. We calculate the joint p.d.f. of the new n variables and integrating with respect to the average we obtain the joint p.d.f. of the other n ‒ 1 variables. One of these variables is transformed in the concentration ratio. We calculate the joint p.d.f. of the concentration ratio and of the other n ‒ 2 variables and at last we integrate this p.d.f. with respect to the n ? 2 variables obtaining the marginal p.d.f. of the concentration ratio. The main difficulty of this procedure consists in the identification of the region of integration of the n ‒ 2 variables, for two reasons: firstly the need to decompose this region into subregions which allow identifying directly the limits of integration and secondly the growing number of such subregions that makes the derivation heavy.

In Sections 3-7, using the software Mathematica, we derive the exact distributions of the concentration ratio for samples from a uniform distribution of size n = 6, 7, 8, 9 and 10. Moreover (Section 8), we find some regularities of such distributions valid for any sample size.

2. The Procedure to Derive the Distribution of the Concentration Ratio

Let random variables 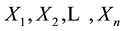from a uniform population have p.d.f.

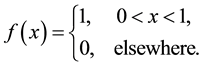(1)

The joint p.d.f. of the variables is

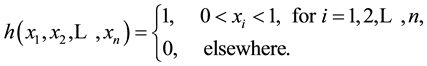(2)

The joint p.d.f. of the order statistics 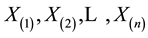is

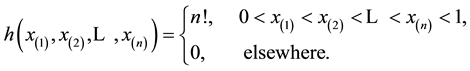(3)

By transforming the variables

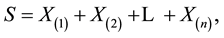
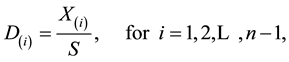
whose Jacobian is

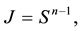
we obtain the joint p.d.f. of the variables S and 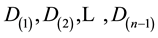that can be written as

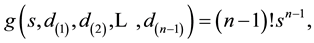(4)

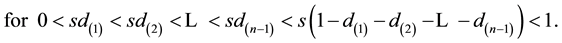
We integrate expression [4] with respect to the variable S and obtain the joint p.d.f. of the variables that can be written as

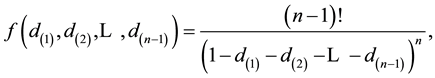(5)

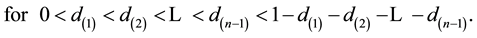
By transforming the variable 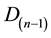in the variable R i.e. the concentration ratio

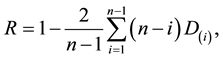
from which we get

the Jacobian of the transformation is

and the joint p.d.f. of the variable R and is

(6)

for

(7)

By integrating expression [6] with respect to the variables over the regions determined by inequalities [7] , we get the marginal p.d.f. of the concentration ratio R.

3. The Distribution of the Concentration Ratio for n = 6

The procedure indicated in Section 2 is used to obtain the following p.d.f. (Figure 1) of the concentration ratio for random samples of size n = 6:

Characteristic values of the distribution are:

mean

second moment

third moment

fourth moment

standard deviation

index of skewness

index of kurtosis

The distribution of the concentration ratio R for samples of size n = 6 from a uniform population shows a slight positive skewness and platykurtosis.

4. The Distribution of the Concentration Ratio for n = 7

The procedure indicated in Section 2 is used to obtain the following p.d.f. (Figure 2) of the concentration ratio R for random samples of size n = 7:

Characteristic values of the distribution are:

mean

second moment

third moment

fourth moment

standard deviation

index of skewness

index of kurtosis

The distribution of the concentration ratio R for samples of size n = 7 from a uniform population shows slight positive skewness and platykurtosis, both lower than those obtained for samples of size n = 6.

5. The Distribution of the Concentration Ratio for n = 8

The procedure indicated in Section 2 is used to obtain the following p.d.f. (Figure 3) of the concentration ratio R for random samples of size n = 8:

Characteristic values of the distribution are:

mean

second moment

third moment

fourth moment

standard deviation

index of skewness

index of kurtosis

The distribution of the concentration ratio R for samples of size from a uniform population shows slight positive skewness and platykurtosis, both lower than those obtained for samples of size and 7.

6. The Distribution of the Concentration Ratio for n = 9

The procedure indicated in Section 2 is used to obtain the following p.d.f. (Figure 4) of the concentration ratio R for random samples of size n = 9:

Characteristic values of the distribution are:

mean

second moment

third moment

fourth moment

standard deviation

index of skewness

index of kurtosis

The distribution of the concentration ratio R for samples of size n = 9 from a uniform population shows slight positive skewness and platykurtosis, both lower than those obtained for samples of size n = 6, 7 and 8.

7. The Distribution of the Concentration Ratio for n = 10

The procedure indicated in Section 2 is used to obtain the following p.d.f. (Figure 5) of the concentration ratio R for random samples of size n = 10:

Characteristic values of the distribution are:

mean

second moment

third moment

fourth moment

standard deviation

index of skewness

index of kurtosis

The distribution of the concentration ratio R for samples of size n = 10 from a uniform population shows slight positive skewness and platykurtosis, both lower than those obtained for samples of size.

8. Some Regularities of the Distributions

The analysis of the p.d.f. for shows some regularities:

● The p.d.f. of the concentration ratio R, for and for samples of size n, can be expressed by

● Furthermore, the p.d.f. of the concentration ratio R, for and for samples of size n, can be expressed by

● The density of the concentration ratio R, for and for samples of size n, is given by

● The density of the concentration ratio R, for and for samples of size n, is given by

● The jth term of the density of the concentration ratio R, denoted as verifies the following symmetry

The coefficients of the terms of the p.d.f. of the concentration ratio R for samples of size multiplied by become the coefficients of the terms of the same p.d.f. for sample of size n.

These results are valid for every sample size and may allow reducing the heavy calculation to determine the p.d.f. of the concentration ratio R.

9. Concluding Remarks

In the present paper we obtain the distributions of the Gini concentration ratio R for samples of size drawn from a uniform population. We use the same method used by Girone [12] to derive the same distributions for samples of size. We obtain the p.d.f. of the concentration ratio R calculating a multiple integral in dimensions for each region from to for. The limits of integration are defined by solving the inequalities of the order statistics divided by the sample mean and expressed in terms of the concentration ratio R for the values assumed in each of such regions. The calculation of the limits of integration is particularly heavy and requires a very long processing time.

The obtained results show that the p.d.f. of the concentration ratio R is given by hyperbolic splines with degree 2 and with nodes in for. Such distributions are unimodal with mean tending to, which is the value of the concentration ratio R for the population, and have decreasing standard deviation. Moreover, the distributions show a slight positive skewness and platykurtosis that tend to decrease as n increases.

Beyond the possibility to obtain similar results for samples of larger size, open problems are the derivation of the exact expression for the mean and the other features of the distribution of the concentration ratio R for random samples of size n drawn from a uniform population.

References