Applied Mathematics
Vol.05 No.19(2014), Article ID:51207,7 pages
10.4236/am.2014.519283
Two New Iterated Maps for Numerical Nth Root Evaluation
Charles Corrêa Dias1, Fernanda Jaiara Dellajustina2, Luciano Camargo Martins2*
1Department of Electrical Engineering, Universidade do Estado de Santa Catarina (UDESC), Joinville, Brazil
2Department of Physics, Universidade do Estado de Santa Catarina (UDESC), Joinville, Brazil
Email: charlamps@hotmail.com, fernandadellajustina@gmail.com, *luciano.martins@udesc.br
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 August 2014; revised 10 September 2014; accepted 6 October 2014
ABSTRACT
In this paper we propose two original iterated maps to numerically approximate the nth root of a real number. Comparisons between the new maps and the famous Newton-Raphson method are carried out, including fixed point determination, stability analysis and measure of the mean convergence time, which is confirmed by our analytical convergence time model. Stability of solutions is confirmed by measuring the Lyapunov exponent over the parameter space of each map. A generalization of the second map is proposed, giving rise to a family of new maps to address the same problem. This work is developed within the language of discrete dynamical systems.
Keywords:
Iterated Map, Nth Root of a Real Number, Numerical Method, Newton-Raphson Method, Dynamical System

1. Introduction
Recent applications of iterated maps in numerical analysis have been found in literature, using and extending the techniques of dynamical systems to the study of numerical algorithms and number theory [1] -[3] . Application in technology and hardware devices are also frequent nowadays [4] - [7] .
We propose and study in this work two new methods for numerical root approximations, both of which based on iterated maps. In the following sections we present a detailed study of each map, their fixed points and stability, the occurrence of bifurcations and chaotic behavior.
Some common tools of nonlinear dynamics [8] [9] are used to the study of the orbits, i.e., the numerical time series obtained for each map are investigated. The numerical approximations 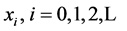 to solve the general equation
to solve the general equation , where
, where 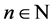 and
and 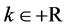 are obtained, but the validity of the results can be extended to
are obtained, but the validity of the results can be extended to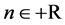 .
.
In Section 2 we present a new map proposed by one of us (C. C. Dias), named as First Dias Map (FDM), showing the existence of a fixed point for roots in the range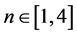 , and that this fixed point corresponds exactly to
, and that this fixed point corresponds exactly to .
.
In Section 3, we generalize the FDM by adding a new parameter for studying the stability of its fixed point by defining a new class of maps called Weighted Average Map (WAM). For this class of maps, we investigate the dependence of the fixed point corresponding to the nth root of 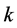 over the parameter space
over the parameter space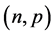 .
.
Finally, in Section 4, we measure and compare the Mean Convergence Time (MCT) for all the studied maps, for 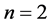 and
and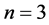 , varying
, varying 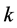 over an uniform grid of initial conditions and computing the average amount of iterations to converge to the root
over an uniform grid of initial conditions and computing the average amount of iterations to converge to the root 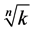 within the standard numerical double precision. An analytical model is proposed and used to confirm the numerical results of MCT with the analytical convergence time (ACT) for the WAM.
within the standard numerical double precision. An analytical model is proposed and used to confirm the numerical results of MCT with the analytical convergence time (ACT) for the WAM.
2. The First Dias Map (FDM)
The map which we will study now was created by Charles C. Dias to extract real roots of numbers numbers, by solving the equation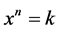 . The proposed map is one-dimensional and is defined as
. The proposed map is one-dimensional and is defined as
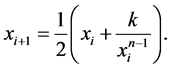 (1.1)
(1.1)
Comparing this with the Newton-Raphson Method (NRM) equation and Babylonian Method (BABM) [10] noticed that this statement is a mixture of both, and the FDM is an arithmetic average between the linear and nonlinear terms in Equation (1.1), and can be used to approximate the nth root of  for
for


The base function that appears in the iterated map defined by Equation (1.1) can be derived dividing 



and adding 
2.1. Geometrical Construction
To construct geometrically the FDM time series, the first step is to find the auxiliary equations of the lines 




that for 

Knowing that their linear coefficients are all





and taking the arithmetic mean between the auxiliary points 

Figure 2(a) shows the cobweb for the FDM time series for 

Figure 1. The FDM schematic geometrical path construction.

Figure 2. The FDM cobwebs for


shows a numerical development of the FDM series for the parameters 

2.2. Fixed Point and Stability Analysis
Solving 

map function


and solving the last equation we have the range of parameter 
2.3. Numerical Results
The FDM time series have different dynamics depending on the parameters
To measure the rate of divergent orbits, i.e., the sensitive dependence on initial conditions, we can use is characteristic Lyapunov exponent

Table 1. FDM time series for 


goes to zero signing the period bifurcations. The yellow to red regions indicate the a positive Lyapunov exponents, the signature of chaos.
The FDM bifurcation diagram, discarded a transient of 103 iterations and plotted the next 500 values of



We also study numerically the FDM return diagrams for different values of the parameter


3. The Weighted Average Map (WAM)
Instead of adding








Adding 

and after collecting 


and solving its fixed point equation 

3.1. Fixed Point and Stability Analysis
Applying the stability criterion [11] , i.e., 



guarantee fixed point stability, and Figure 4 shows the line corresponding to this condition, below which the fixed point is unstable. As 

3.2. WAM Subclasses and Hierarchy
A special subclass of WAM is FDM, when





Figure 3. (a) FDM Lyapunov exponent over the parameter space






Figure 4. For
at


For NRM, the derivative of the mapping function at the fixed point is null, satisfying the stability criterion and resulting in the most efficient rate of convergence of the time series near the fixed point. When the starting point 



From the definition of the Lyapunov characteristic exponent for a unidimensional map we conclude that the derivative of the mapping function at the fixed point 








4. Mean Convergence Time (MCT)
This section reports the numerical results for the mean convergence time (MCT) for NRM, FDM and WAM, based on the average number of iterates to converge within different precisions









In Figure 6(a) we see that the NRM MCT is close to 4, which means that after 4 iterations, on average, there has been convergence to the root. From this figure, we conclude that FDM is around 10 times slower than NRM, and WAM is around has twice the speed of FDM. In this test, the most efficient is NRM, with the lowest MCT.
Both NRM and FDM belong to the same WAM family, as discussed in Section 3, and the stability of the fixed point 




Figure 5. Hierarchy of the WAM subclasses.

Figure 6. Numerical results of MCT for cubic roots 




optimal value of the parameter





We can see in Figure 4(a) that, as we approach the line that corresponds to the weighting term, NRM shows the minimum MCT over this line and therefore the most efficient of all studied maps is the NRM.
Summarizing the key information about NRM, FDM and WAM, with the numerical results for the MCT within double precision for these maps, for the parameters 

Analytical Convergence Time Model
The Lyapunov characteristic exponent for a unidimensional map 
can be approximate by 

For WAM, it is easy to show that







Using the original Lyapunov’s idea, the characteristic exponent 








Applying the natural logarithm to both sides of the above equation we have 
iterations needed to reduces the error in the second orbit to

valid for any fixed point of a unidimensional map, where the approximated 
Applying this model to our more general map (WAM), we have

of the parameters 

Table 2. MCT numerical results for NRM, FDM and WAM maps.
5. Conclusions
In the study of iterated maps to extract the real root of real numbers we have applied some common tools from nonlinear dynamics that allowed us to predict the fixed point of the studied maps associated with the nth root of
We conclude, through the geometric argument used to recover the original analytical form of FDM, that both NRM and FDM can be reduced to averages between two terms, one linear and other nonlinear. From this observation, we generalize the original FDM idea to a new family of maps on which we add a new parameter


The mean convergence time (MCT) numerical results indicate that NRM is the most efficient subclass of the more general weighted average map (WAM) proposed in this work, as pointed out in Figure 4(a), over the line
The main results of this work are obtained for

Acknowledgements
This work was partially supported by the Brazilian agency Conselho Nacional de Desenvolvimento Cientfico e Tecnológico―CNPq and Universidade do Estado de Santa Catarina―UDESC.
References
- Faber, X. and Voloch, J.F. (2011) On the Number of Places of Convergence for Newton’s Method over Number Fields. Journal de Theorie des Nombres de Bordeaux, 23, 387-401.
- Grau-Sánchez, M. and Daz-Barrero, J.L. (2011) A Technique to Composite a Modified Newton’s Method for Solving Nonlinear Equations. ArXiv e-prints.
- Pan, B., Cheng, P. and Xu, B. (2005) In-Plane Displacements Measurement by Gradient-Based Digital Image Correlation. SPIE Proceedings, 5852, 544-551.
- Amin, A.M., Thakur, R., Madren, S., Chuang, H.-S., Thottethodi, M., Vijaykumar, T., Wereley, S.T. and Jacobson, S.C. (2013) Software-Programmable Continuous-Flow Multi-Purpose Lab-on-a-Chip. Microfluidics and Nanofluidics, 15, 647-659. http://dx.doi.org/10.1007/s10404-013-1180-2
- Mungan, C.E. and Lipscombe, T.C. (2012) Babylonian Resistor Networks. European Journal of Physics, 33, 531. http://dx.doi.org/10.1088/0143-0807/33/3/531
- Senthilpari, C., Mohamad, Z.I. and Kavitha, S. (2011) Proposed Low Power, High Speed Adder-Based 65-nm Square Root Circuit. Microelectronics Journal, 42, 445-451. http://dx.doi.org/10.1016/j.mejo.2010.10.015
- Sun, T., Tsuda, S., Zauner, K.-P. and Morgan, H. (2010) On-Chip Electrical Impedance Tomography for Imaging Biological Cells. Biosensors and Bioelectronics, 25, 1109-1115. http://dx.doi.org/10.1016/j.bios.2009.09.036
- Ausloos, M. and Dirickx, M. (2005) The Logistic Map and the Route to Chaos: From the Beginnings to Modern Applications. Springer, New York.
- Eve, J. (1963) Starting Approximations for the Iterative Calculation of Square Roots. The Computer Journal, 6, 274- 276. http://dx.doi.org/10.1093/comjnl/6.3.274
- Dellajustina, F.J. and Martins, L.C. (2014) The Hidden Geometry of the Babylonian Square Root Method. Accepted by Applied Mathematics, August.
- Lyapunov, A.M. (1992) The General Problem of the Stability of Motion. International Journal of Control, 55, 531- 534. http://dx.doi.org/10.1080/00207179208934253
- Schuster, H.G. and Just, W. (2005) Deterministic Chaos: An Introduction. 4th Edition, John Wiley & Sons, New York. http://dx.doi.org/10.1002/3527604804
NOTES
*Corresponding author.








