Received 16 July 2014; revised 8 August 2014; accepted 1 September 2014

ABSTRACT

In this paper, a reaction-diffusion equation with discrete time delay that describes the dynamics of the blood cell production is analyzed. The existence of the traveling wave front solutions is demonstrated using the technique of upper and lower solutions and the associated monotone iteration.

Keywords:

Traveling Wavefronts, Hematopoiesis Model, Time Delay

1. Introduction

It is well know that the traveling wave theory was initiated in 1937 by Kolmogorov, Petrovskii, Piskunov [1] and Fisher [2] . Now, the theory of traveling wave solutions to reaction-diffusion equations is one of the fast developing areas of modern mathematics and has attracted much attention due to its significance in biology, chemistry, epidemiology and physics, see [3] [4] and the reference cited therein. In recent years, the traveling wave problem for reaction-diffusion systems with delay has been widely studied. For example, Gomez and Trofimchuk [5] considered the Fisher-KPP equation and their results showed that each monotone traveling wave could be found via an iteration procedure by using the special montone integral operators. Schaaf [6] systematically studied two scalar reaction-diffusion equations with a single discrete delay by using the phase plane technique, the maximum principle for parabolic functional differential equations and the general theory of ordinary differential equations. The degree theory has been adopted in [7] [8] .

In this paper we consider the following reaction-diffusion equation with a discrete time delay:

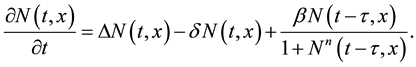(1.1)

When 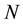is independent on the spatial variable, the above equation reduces to the following ordinary differential equation

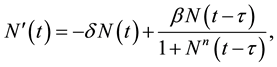(1.2)

which was first proposed by Mackey and Glass [9] to describe the dynamics of blood cell production. Here, 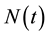denotes the density of mature stem cells in blood circulation and 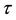is the time delay between the production of immature stem cells in bone marrow and their maturation for release in the circulating blood stream; 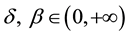and 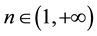are positive constants that represent some specific meanings in blood circula-

tion. For instance, 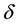is the lost rate of the cells from the circulation. The term 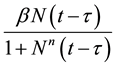shows that the

flux of the cells into the circulation from the stem cell compartment depends on the number of cells 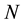at time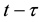. For more details about Hematopoiesis model, we refer the readers to the articles of Mackey [9] -[11] and the references given in them.

Equation (1.2) has been studied by many authors such as in [12] -[14] . Weng and Dai [13] proved that the positive equilibrium to Equation (1.2) could be a global attractor under some conditions. Wu, Li and Zhou [14] derived a sufficient and necessary condition that guarantees the existence of positive periodic solutions of Equation (1.2) with periodic coefficients.

Equation (1.2) can be generalized as the following functional differential equation

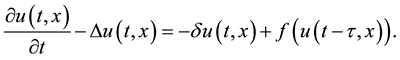(1.3)

Wang [15] investigated the generalized equation with Neumann boundary condition and obtained the oscillatory behavior of solutions about the positive equilibrium of (1.3). Further, they derived the sufficient and necessary conditions for global attractivity of the zero solution. In addition, global attractivity of the positive equilibrium of (1.3) was investigated by Gopalsamy and Kulenvic [16] . Cheng and Zhang [17] and Jiang et al. [18] (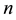-dimentional case) instead investigated the existence of positive periodic solutions of Equation (1.3) by using the Krasnosel skii fixed point theorem.

The aim of this paper is to consider the existence of traveling wave front solutions for (1.1) in the case of one dimensional space.

This paper is outlined as follows. The next section, we will introduce the technique of upper and lower solutions developed by Wu and Zou [19] . The conditions for establishing the positive equilibria and obtaining the existence of traveling waves are derived in Section 2.

To investigate the existence of traveling wave fronts of (1.1), we describe briefly the technique of upper and lower solutions developed by Wu and Zhou [19] .

Consider a scalar reaction-diffusion equation with time delay:

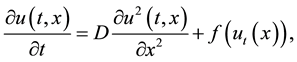(1.4)

where, and is the diffusion coefficient. The function is continuous and is an element in parameterized by and given by

Looking for traveling wave solutions of the form leads to a second-order functional differential Equation

(1.5)

where is define by

Now we assume that

A1. There exists such that and for, where denotes the constant function taking the value on.

A2. There exists such that

for with.

If for some, (1.5) has a monotone solution defined on such that

(1.6)

then is called a traveling wave front of (1.4) with a wave speed.

Define a profile set for traveling wave fronts of (1.1) by

The upper and lower solution for (2.1) are defined as follows:

Definition 1 The piecewise smooth functions and in are called upper and lower solution of (1.4) if and if

and satisfies the above differential inequalities in reversed order.

Now we are in the position to state a scalar version of [19] (Theorem 3.6).

Theorem 1 If the conditions (A1) and (A2) hold, suppose that (1.5) has an upper solution in and a lower solution (which is not necessarily in) with and in, then the problem (1.4) admits a traveling wave front.

2. Existence of Traveling Wave Fronts

Assume that, and we can get two equilibria of (1.1)

We will tackle the existence of solutions of (3.1) with the asymptotic boundary condition

which corresponds to the traveling wave fronts of (1.2) connecting and.

Substituting into (1.2), and denoting the movingvariable still by, the resulting wave equation becomes

(1.7)

Define the function

Lemma 1 If, then, and, for any, where denotes the constant function taking the value on.

Next we show that satisfies quasi-monotonicity condition with some assumptions.

Lemma 2 If, , then satisfies the following quasi-monotonicity condition:

Take, and we have

for all with,.

Proof 1 Consider the function, and it is obvious that

If, then

since.

It demonstrates that the function is increasing on. A direct computation shows that

and then

Therefore, if choosing, we have

.

This completes the proof.

Remark 1 If, the function is increasing for all. When the condition (A2)

is hold.

Define the profile set

Next we will discuss the existence problem by using the method of upper and lower solutions that are defined as follows:

Definition 2 The piecewise smooth functions and in are called upper and lower solution of (3.1) if and if

and satisfies the above differential inequalities in reversed order.

Define

,

then we have the following lemmas.

Lemma 3 There exists such that for, has two positive real roots, and

Since the proof of this lemma is similar to that of Claim 2.3 of [19] , we omit it. Next we first construct the upper solution of (3.1).

Lemma 4 Assume, then is an upper solution of (3.1) and.

Proof 2 It is easy to verify that. We show that is an upper solution of (3.1).

Let be such that.

i) For, , , ,. thus

ii) For, and, thus

According to the discussion above, we know that is an upper solution of (1.5). This completes the proof.

We now give the lower solution to (1.5). Let and be the same as those given in Lemma 3.2. Take such that. Define, where the constant is to be determined.

Lemma 5 For, is a lower solution for Equation (3.1).

Proof 3 Let, then for and

i) For, , and. Hence

ii) For, we have

It is easy to check that. It follows that. Therefore

Note that

Since, we have. Thus

If we choose

then. Thus is a lower solution of (3.1).

It is clear that. Summarizing the above conclusions, we give our main result of this paper below.

Theorem 2 If, , or, then for every, the problem (1.2) has a traveling wave front which connects the equilibria and.

References

NOTES

^*Corresponding author.