Applied Mathematics
Vol.05 No.15(2014), Article ID:48595,7 pages
10.4236/am.2014.515217
To Problem of the Rewinding of the Tape with Automatically Adjustable Influences
Muhsin Kh. Teshaev
Bukhara Engineering-Technological Institute, Bukhara, Republic of Uzbekistan
Email: muhsin_5@mail.ru, muhsin.teshayev@rambler.ru
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 May 2014; revised 3 July 2014; accepted 16 July 2014
ABSTRACT
In this work the problem of rewinding of a tape with constant speed is considered. Considering that drums represent bodies of variable weight, the equations of motion of system are formulated. Taking into account parametrical clearing of system of servo-constraints, the structure of force of reaction of servo-constraints which provides steady realization of servo-constraints (a constancy of linear speed of a tape) is defined. For realization of servo-constraints, it is offered to build digital watching system (DWS) and the full system of equations of DWS is formed. Laws of change of the operating influences, systems providing stability under the relation of the variety defined of servo-constraints are defined.
Keywords:
Rewinding of Tape, Servo-Constraint, Speed, Force of Reaction of Servo-Constraints, Parametrical Clearing, Stability, The Digital Watching System, Full System of the Equations

1. Introduction
For the first time the concept idea of servo-constraints has been entered into analytical dynamics by H. Beghin [1] . The methods used by H. Beghin, had the further development in P. Appel’s [2] works, A. Przeborski’s [3] , V. S. Novoselov’s [4] , M. F. Shulgin’s [5] , V. V. Rumjantsev’s [6] [7] , V. I. Kirgetov’s [8] , A. G. Azizov’s [9] [10] and others.
Appendices of methods of analytical dynamics to a wide range of specific targets demand the account and other features connected with steady realization of servo-constraints, and that for such systems it is impossible to distract from a way of their realization.
S. S. Nugmanova’s attention for the first time has been paid to this circumstance [11] . Following the theory of parametrical clearing [12] , and the theory of the compelled motions [13] constructed the theory, allowing to develop the area of practical applicability of methods of analytical mechanics of systems with servo-constraints, including questions of their steady realization [14] [15] . In works [16] [17] the equations of motion of the systems, interfered by constraints of the first and second sort are deduced, and also the obvious kind of forces of reactions of servo-constraints is defined.
In this article the results of works [16] [17] are illustrated to the problem of rewinding of a tape.
2. Forming the Equation of Motion and Refining the Servo-Constraints’ Forces of Reaction
Let’s consider process of rewinding of a tape (Figure 1). Rewinding of a tape from the drum 3 on a drum 2 is carried out by means of electric machine (EM) of a direct current of the independent excitation operating through a reducer with transfer number
 on a drum 2. On Figure 1 the feedback providing a constancy of linear speed of motion of tape u = сonst and forming of stabilizing pressure on an input of the electric machine (EM) are illustrated. As well as, from the work of Zijatdinov R. M. (1983) [18] , we will divide the scheme Fig- ure 1 on two parts on a dashed line. Kinetic energy of system looks like as:
on a drum 2. On Figure 1 the feedback providing a constancy of linear speed of motion of tape u = сonst and forming of stabilizing pressure on an input of the electric machine (EM) are illustrated. As well as, from the work of Zijatdinov R. M. (1983) [18] , we will divide the scheme Fig- ure 1 on two parts on a dashed line. Kinetic energy of system looks like as:
 (1)
(1)
where ―the moments of inertia of a reducer both corresponding drums;
―the moments of inertia of a reducer both corresponding drums;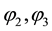 ―angles of rotation of drums 2 and 3.
―angles of rotation of drums 2 and 3.
As drums 2 and 3 represent bodies of variable weight it is necessary to take the general equation of dynamics in the form showed in Bessonov A. P. (1967) [19] :
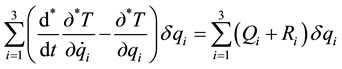 (2)
(2)
where for
 co-ordinates
co-ordinates
 are designated;
are designated; −the generalized force appropriated to co-ordinate
−the generalized force appropriated to co-ordinate ;
; ―the generalized reactive force, which looks like
―the generalized reactive force, which looks like
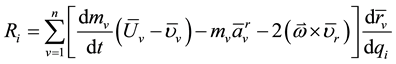
here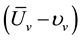 ―relative speed of joining particles;
―relative speed of joining particles; ―particle acceleration in motion concerning the system of co-ordinates connected by a link, and the symbol “*” above specifies that differentiation is made according to a hardening principle.
―particle acceleration in motion concerning the system of co-ordinates connected by a link, and the symbol “*” above specifies that differentiation is made according to a hardening principle.

Figure 1. Process of rewinding of a tape.
If relative speed of joining particles is equal to zero, and there is no relative motion of joining particles concerning a drum 2, according to Bessonov A. P. [16] (1967) we conclude that:
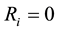
On system, according to assumptions, one ideal geometrical constraint
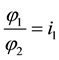 (3)
(3)
and one kinematical servo-constraint in Beghin H. (1967) [1]

is imposed, where

Taking into account (3) kinetic energy (1) systems we will lead to a formula

On possible moving constraint (3) imposes restriction [7] :

From a way of action of servo-constraint (4) follows that, moving, on which servo-constraint works do not make reaction, look like in Beghin H. (1967) [1] :

We will consider the right part from a dashed line. Considering that for the right part,

where


where
Considering that for the left part

where


To the received system of the Equations (9), (11) adding one kinematical equation,

will be received system of three Equations (9), (11), (12) concerning unknown persons
Consider a case, when rewinding is carried out with constant brake moment

As it is known [9] [10] , servo-constraints are carried out not precisely and therefore, along with (4) the have occurrence parity

where
Having for an object steady realization of servo-constraint (4), the received system of the equations will be added to (9), (11), (12) equation [9] [10] :

and reaction compulsion


where

Thus, the system of the Equations (9), (11), (12), (16) describes dynamics of adjustable process of rewinding of a tape concerning variables




and substituting it in (9), the following equation will be received:

Taking into account (12), Equation (17) can be led to the following:
3. Stability
If a reaction of servo-constraint

where
Taking into account a parity (13), last equation will look like:

Considering

Taking into account (20), Equation (19) will look like

where

Apparently, from (22) the Equation (21) represents the differential equation with variable factors. Stability of its zero decision


where

In expression (24) constant number


had a negative material part. This condition, according to Hurvits’s criterion [21] , will look like
which is reduced to a condition

Lyapunov’s definitely positive function


Its full derivative on time, worked out owing to the equation of the indignant motion (23), will look like:
Let’s calculate:

Then the condition of certain positively of the form―
which it is reduced to a condition

Condition (26) show that, for maintenance of steady realization of servo-constraint (4) moment of the electric machine




4. The Realization of Servo-Constraints
We will consider a realization problem of servo-constraint (4) by electromechanical digital watching system (DWS) [20] for which executive element we accept the engine of a direct current of independent excitation. Its full system of the equations will look like [17] :





where










The law of formation of the operating influences DWM providing stability of motion of system in relation to servo-constraint (4) is defined by the decision of system of the equations:





rather of

Substituting the law (29) in (27), results the Equation (21). Hence, the law (28) provides asymptotically stability of motion of system under the relation of the variety defined by servo-constraint (4).
Along with the generalized model, we will consider the simplified model of watching system [17] [18] , i.e. at assumptions,

from (28) we will receive the law of formation of operating influences DWM for simplified model DWS:

Substituting the law (31) in (27) at the same assumptions (30) we will receive the Equation (21), which stability conditions looks like (26).
References
- Beghin, H. (1967) The Theory of Hygroscopic Compasses. Nauka Press, Moscow, 5-31.
- Appel, P. (1925) Sur les une forme generale des equations de la dynamique (memorial des Sciences Mathematique, fasccule 1). Paris, 1-50.
- Przeborski, A. (1902) Die allgemeinsten Gleichunden der Klassischen Dunamik. Mathematische Zeitschrift, 36, 184- 194. http://dx.doi.org/10.1007/BF01188619
- Novoselov, V.S. (1969) New Settlers Nonlinear Nonholonomic Co-Ordinates in the Analytical Mechanics. Leningrad State University, 217, 50-83.
- Shulgin, M.F. (1958) About Some Differential Equations of Analytical Dynamics and Their Integration. The Central Asian State University Press, Tashkent, 73-94.
- Rumyantsev, V.V. (1961) About Motion of Some Systems with Nonideal Constraints. The Moscow State University bulletin, Series, Маthematics and Меchаnics, 61-66.
- Rumyantsev, V.V. (1976) About Motion of Operated Mechanical Systems. The Journal of Applied Mathematics and Mechanics, 5, 771-781.
- Kirgetov, V.I. (1967) About Motion of Operated Mechanical Systems with Conditional Constrains (Servo-Constraints). The Journal of Applied Mathematics and Mechanics, 3, 433-446.
- Azizov, А.G. (1975) About the Equations of Dynamics of Systems with Servo-Constraints. Proceedings of Tashkent State University, 476, 67-75.
- Azizov, A.G. (1980) Applied Problems of Dynamics of Operated Systems. Tashkent State University, Tashkent, 1-28.
- Nugmanova, Sh.S. (1953) About the Equations of Motions of Adjustable Systems. The Kazan Aviation Institute, 27, 26-35.
- Chetaev, N.G. (1962) About a Principle of House. In: Chetaev, N.G., Ed., Stability of Motion. Works on the Analytical Mechanics, Academy of Science of the USSR, 329-334.
- Chetaev, N.G. (1962) On the Compelled Motions. In: Chetaev, N.G., Ed., Stability of Motion. Works on the Analytical Mechanics, Academy of Science of the USSR, 311-316.
- Krasovsky, N.N. (1959) Some of Problems of Theories of Stability of Motion. Fizmatgiz, Moscow, 17-139.
- Lure, A.I. (1961) Analytical Mechanics. Fizmatgiz, Moscow, 13-430.
- Teshaev, M.Kh. (1999) About Stabilization of the Mechanical Systems Constrained by Geometrical Constriets. The Uzbek Magazine “Problems of Mechanics”, 1, 7-20.
- Teshaev, M.Kh. (2005) About Designing of Reactions of Servo-Constraints the Systems Constrained by Kinematical Constraints. The Uzbek Magazine “Problems of Mechanics”, 1, 3-7.
- Ziyatdinov, R.M. (1980) Dynamic of Machine Units with Automatically Adjustable Variators. Tashkent, 1-23.
- Bessonov, A.P. (1967) Bas of Dynamics of Mechanisms with Variable Weight of Links. The Nauka, Moscow, 84-102.
- Medvedev, V.S. (1979) Designing of Watching Drives by Means of the COMPUTER. Mechanical Engineering, Moscow, 47-62.
- Merkin, G.D. (1987) Introduction to Theory of Stability. The Nauka, Moscow, 1-304.














