Applied Mathematics
Vol.05 No.06(2014), Article ID:44586,12 pages
10.4236/am.2014.56086
Paraconsistent Differential Calculus (Part I): First-Order Paraconsistent Derivative
João Inácio Da Silva Filho1,2
1Group of Applied Paraconsistent Logic, Santa Cecília University-UNISANTA, Santos, Brazil
2Institute for Advanced Studies, University of São Paulo-IEAUSP, São Paulo, Brazil
Email: inacio@unisanta.br
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 January 2014; revised 21 February 2014; accepted 28 February 2014
ABSTRACT
A type of Inconsistent Mathematics structured on Paraconsistent Logic (PL) and that has, as the main purpose, the study of common mathematical objects such as sets, numbers and functions, where some contradictions are allowed, is called Paraconsistent Mathematics. The PL is a non- Classical logic and its main property is to present tolerance for contradiction in its fundamentals without the invalidation of the conclusions. In this paper (part 1), we use the PL in its annotated form, denominated Paraconsistent Annotated Logic with annotation of two values―PAL2v for present a first-order Paraconsistent Derivative. The PAL2v has, in its representation, an asso- ciated lattice FOUR based on Hasse Diagram. This PAL2v-Lattice allows development of a Para- consistent Differential Calculus based on fundamentals and equations obtained by geometric interpretations. In this first article it is presented some examples applying derivatives of first- order with the concepts of Paraconsistent Mathematics. In the second part of this work we will show the Paraconsistent Derivative of second-order with application examples.
Keywords:
Paraconsistent Logic, Paraconsistent Annotated Logic, Paraconsistent Mathematics, Paraconsistent Differential Calculus

1. Introduction
There is no doubt that one of the greatest achievements in the area of applied mathematics was the Differential Calculus. The construction of Differential Calculus demonstrates the genius of Newton and Leibniz, as well as other physicists, philosophers and mathematicians who preceded or succeeded them. However, in Infinitesimal Calculus, when using the infinitesimal ε we know that even being infinitely small it is not zero, but regardless of this fact that ε simply disappears at the end of calculation [1] - [4] . This shows that reasoning in Differential Calculus is done with conflicting information and in these calculations ε is despised so that it does not cause conflicts in the conclusions [5] .
The Classical Logic, which emerged in Greece with the ancient philosophers, brings in its fundamentals bi- nary strict laws that do not consider the existence of contradiction, and therefore do not respond well to certain conditions frequently encountered in the real world. From this, it appears that there is the need of finding new ways to design models of physical systems which may prove more efficiency to respond to analysis, particularly those dealing with boundary extreme conditions that are based on information signals which can be contradic- tory [6] . Responding to this problem, today there are many logics different from the Classical aiming to structure models that respond adequately the information from an imperfect world represented by the data information that could be incomplete and/or contradictory [6] - [8] . These logics are known as non-Classical and bring in its fundamental principles that somehow violate the laws that underlie the Classical Logic [6] [9] [10] . Mathemati- cal theories supported by these non-Classical logics that, in certain aspects, contradict the rigid binary laws of Classical Logic, have been quite effective in various fields of knowledge. The Paraconsistent Logic (PL), which originates mathematics used in this work belongs to the class of non-classical logics and presents in its founda- tion some tolerance at contradiction that occurs, without invalidating the conclusions. Its extended form, called Para-consistent Annotated Logic (PAL), has in its representation as an associated Lattice that allows the devel- opment of algorithmic techniques and direct applications, and that has brought promising results [6] [9] - [12] .
In this paper, we use the PAL in its structural form in which an annotation of two values is used to perform a type of Differential Paraconsistent Calculus applied in solving problem related to physical systems. The PAL treating information signals in its special form, called Paraconsistent Logic with annotation of two values (PAL2v), allows extracting from the Newton’s quotient, found in the deduction of the differential calculus. All the information is necessary and sufficient to effect the derivative of first- and second-order and apply them to physical systems with good results without ignoring the action of the infinitesimal [6] [12] .
2. A Non-Classical Paraconsistent Logic
Into the family of the non-Classical logics we have Paraconsistent logics whose main feature is the revocation of the principle of non-contradiction. In formal way [10] [11] , we can define Paraconsistent Logic as Any deduc- tive theory T is based on a given logic L, and we suppose that all logics considered here contain a connective for negation, symbolized. If two formulas of the language of T, one of which is the negation of the other, are both theorems of T (i.e. for some formula A, both A and A are theorems of T), then T is said to be inconsistent, oth- erwise T is consistent. If all formulas of the language of T (or all closed formulas) are theorems of T, then T is called trivial; otherwise it is said to be non-trivial. A logic L is paraconsistent if it can be the underlying logic of inconsistent, but non-trivial theories. The usual systems of logic, for instance classical and intuitionistic logics, are not paraconsistent. If the theory T is inconsistent and non-trivial, then T is called a paraconsistent theory.
Therefore, Paraconsistent Logic is a non-Classical Logic repealing the principle of non-contradiction and al- lows the processing of conflicting information in its theoretical structure. Among the precursors of Paraconsis- tent Logic is the polish logician J. Lukasiewicz and the Russian philosopher N.A. Vasilev that independently suggested the possibility of a logic that restrict, for example, the principle of contradiction. The initial systems of Paraconsistent Logic containing all logical levels, involving propositional calculations, of predicate and de- scriptions, as well as logic from superior order is due to N.C.A. Costa (1954 onwards) [6] [13] [14] . Currently there are even paraconsistent systems of theories of sets, strictly stronger than the classic, being then considered as paraconsistent subsystems [15] .
2.1. Paraconsistent Annotated Logic PAL
Paraconsistent Annotated Logic―PAL, also known as evidential logic ετ, belongs to the family of Paraconsis- tent Logics and can be represented in a particular way, through a four-vertices Lattice (Lattice FOUR). In intuitive mode the constants of annotation represented in its vertices will give connotations of Logical states related at propositions P [6] [12] [15] .
2.2. Paraconsistent Annotated Logic with Annotation of Twos Values―PAL2v
An atomic proposition of PAL-logic language can be represented by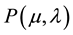 , where μ and λ are elements in the closed interval [0,1] what belongs to the set of real numbers [6] [10] . These two values are considered in- formation Signals and called of degrees of evidence. Among several intuitive readings,
, where μ and λ are elements in the closed interval [0,1] what belongs to the set of real numbers [6] [10] . These two values are considered in- formation Signals and called of degrees of evidence. Among several intuitive readings,
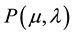 , can be read as: µ is the evidence favorable to proposition P and λ the unfavorable evidence to proposition P.
, can be read as: µ is the evidence favorable to proposition P and λ the unfavorable evidence to proposition P.
In [10] and [13] were introduced some terminology. The pair
 is called constant annotation. Such a pair is an element of [0,1] × [0,1] that sometimes indicated by [0,1]2, where [0,1] indicates the closed unitary real interval. For this set is applied one relation of order, so defined:
is called constant annotation. Such a pair is an element of [0,1] × [0,1] that sometimes indicated by [0,1]2, where [0,1] indicates the closed unitary real interval. For this set is applied one relation of order, so defined:
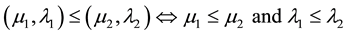 (where the second order is the usual order of real numbers). Therefore, the unitary square with the relation of order constitutes a Lattice
(where the second order is the usual order of real numbers). Therefore, the unitary square with the relation of order constitutes a Lattice
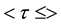 that can symbolize for
that can symbolize for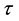 as seen in Figure 1(a).
as seen in Figure 1(a).
Properties:
1) "
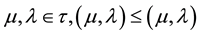 (Reflexivity).
(Reflexivity).
2) "
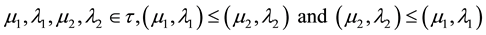 imply
imply
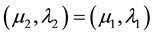 anti-symmetry.
anti-symmetry.
3) "
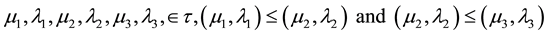 imply
imply
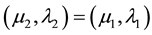 transitivity.
transitivity.
4) "
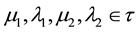 there is the Supremum of
there is the Supremum of
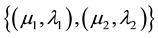 indicated by
indicated by
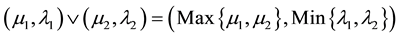 .
.
5) "
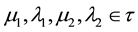 there is the Infimum of
there is the Infimum of
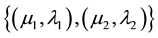 indicated by
indicated by

6) "
As proposed in [10] and in [14] , in this work we use the Lattice FOUR (Hasse diagram) for representation of Paraconsistent Annotated Logic. It is possible through a Lattice FOUR of values obtain in the PAL representa- tion, how much the annotation (or evidences), can express the knowledge about a proposition P. As seen in Figure 1(b) for the PAL t and F represent the classical values true and False, respectively, and T denote Incon- sistent, while ^ indetermination. The Lattice can be formed of ordered pairs of values (m, λ), which will form the annotation. In this representation, an operator ~ is fixed:


3. Paraconsistent Geometric Transformations
Geometric Modeling provides a mathematical description of a geometric object―point, line, conic section, sur- face, or a solid. Geometric transformation is very important for computer graphics, enabling us to manipulate the shape, size, and location of the object [16] . A transformation [3] [4] of a non-empty set U in a non-empty set V is a matching T where, every element x of U, associates a single element y = T(x) of V. Is denoted F: U→V the set of elements y for which there is a x such that T(x) = y it is called image of T. The set U it is called domain and the set V it is called against domain of T. The Paraconsistent transformations are initially made in U = V = R2.
Consider that Unitary Square on Cartesian Plane (USCP) (Figure 1) is the Lattice τ with the coordinate sys- tem where the values of the degree of evidence favorable (m) are represented on the x-axis, and the values of the

Figure 1. (a) Unitary Square on the Cartesian Plane (USCP). (b) Lattice FOUR (Hasse Diagram).
degree of evidence unfavorable (λ) in the y-axis. In this system certain annotation (m, λ) can be identified with the point of the plane in another k system with representation in Hasse Diagram (Figure 2) denominated τ. It is fixed, therefore, a coordinate system for τ and it is defined transformations between USCP and PAL2v-Lattice, which will be the PAL2v-Lattice τ provided with another coordinate system [6] [11] [14] .
The Paraconsistent geometric transformations are made between the USCP-Lattice k (Figure 1), such that PAL2v-Lattice τ (Figure 2) can be obtained from USCP. As shown below, three phases are required to obtain the Paraconsistent transformations. They are: 1) expansion of the scale; 2) rotation; 3) translation the x axis [6] .
1) Expansion
Expansion of the scale consist change of scale enables the change object size.
Consider a point P(x, y) and P'(X, P) the coordinates of the point after scaling [16] . For the change of scale multiplies each point Pi of the object in question by a factor of change of scale horizontally (Sx) and a factor of scaling vertically (Sy). Defining the function T as being:
Is made an increase of the scale at USCP-Lattice k seen in the Figure 1, such that:
Therefore, being:


2) Rotation
The mathematical expression of the rotation of an object from the origin a certain angle θ is considered from a point P(xp, yp), such that:


For Paraconsistent transformation is made in the USCP-Lattice k a Rotation of 45˚ relating to the origin, therefore:

From



3) Translation
Consider a geometric object represented by a set of points Pi belonging to R2 [16] . The translation is made by
Figure 2. Paraconsistent geometric transformation.
adding whole amounts to their coordinates. So, be a point P(x, y) which will be carried out an operation of translation and is P' the coordinates of the point after the translation one can define the function T as being:


With:

Therefore:

where: m Favorable Evidence Degree.
λ Unfavorable Evidence Degree.
Its values, which belong to the set  vary in closed interval −1 to +1 and are in the horizontal axis of the PAL2v-Lattice τ of values called “Axis of degrees of certainty”.
The second term Y3 obtained in the ordered pair of the equation of the transformation (1) is called Contradic- tion Degree (Dct). Therefore, the Contradiction Degree is obtained by:

The resulting values of Dct belong to set Â, vary on the closed interval +1 and −1 and are exposed on the ver- tical axis of the PAL2v-Lattice τ called “Axis of contradiction degrees”.
In the PAL2v-Lattice τ when DC results in +1 it means that the Paraconsistent logical State (eτ) resulting from paraconsistent analysis is True, and when DC results in −1 it means that it is False. Similarly, when Dct results in +1 means that the Paraconsistent logical State (eτ) resulting from the paraconsistent analysis is Inconsistent T, and when Dct result in −1 means that it is Undetermined ^. Figure 2 shows the steps for Paraconsistent Geome- tric Transformation. It is considered, therefore, that by analyzing the PAL2v-Lattice τ [6] [10] [14] the concept of Paraconsistent logical state (eτ) can be correlated to the fundamental concept of state, as studied in physical science and then extended to the model based on Paraconsistent Logic.

Or

where: eτ is the Paraconsistent Logical state.
DC is the Certainty Degree obtained according to the two degrees of Evidence μ and λ.
Dct is the Contradiction Degree found according to the two degrees of Evidence μ and λ.
In a static measurement of observable variables in the physical world, in which is obtained the values of Fa- vorable Evidence Degree (μ) and Unfavorable Evidence Degree (λ) to determine the Certainty Degree (DC) and Contradiction Degree (Dct) is always found a single Paraconsistent Logical State (eτ) related to the two informa- tion signals.
The representation of Observable Variables measured in the physical world and the Paraconsistent Universe represented by PAL2v-Lattice τ can be shown according to the Figure 3.
The Certainty Degree normalized from the Paraconsistent Logical Model is called Resulting Degree of Evi- dence [6] which is calculated by:

Likewise, the normalized Contradiction Degree from the Paraconsistent Logical Model [17] - [19] is calculated by:

Figure 3. Representation of Physical World interacting with Paraconsistent Universe consi- dered by PAL2v-Lattice τ.
Paraconsistent Inverse Transformation
The Paraconsistent Logical Model allows the results to be reversible, so once obtained the values of the Certainty Degree (DC) and Contradiction degree (Dct) it is possible to recover the Degrees of Evidence from the equations: From equation (2):
From Equation (3):
From Equation (2):
From Equation (3):
4. Paraconsistent Mathematics
The Newton’s quotient can adapt to a Paraconsistent Logical Model in the form of Paraconsistent mathematical Model will be formed based on the initial concepts of the derivatives [2] [3] [20] .
4.1. Derivative
If a function f is derivable or differentiable [2] [20] [21] so close to each a point of its domain the function

slope of this line is the derivative of the function f at the point a, and is represented by:


Calculus for the resolutions of problems of Physics the derivative represents the instantaneous variation of a function [2] [19] . Formally we have: Let I be an interval with more than one point of the set of real numbers



function f at point a, and is represented by




4.2. Newton’s Quotient
It is considered the Figure 4 below [2] [20] [21] where the tangent line is defined by the graph of a function f in the point P, as that which passes through P and whose slope (angular coefficient on a straight line) is equal to k. Where P is a fixed point and a Q point that approximates P, occupying successive positions Q1, Q2, Q3..., the secant lines will have the positions by PQ1, PQ2, PQ3... The slopes of these secant lines will be increasingly close to the slope of the tangent line. The analytical tool to make Q approach to P consists in making h tend to zero, that is, taking the h values arbitrarily close to 0. In general it is considered that, in the limit, when the two points of intersection with the graph of f converge to the same point P, the slope of the secant line is equal to the tangent. In this case, the slope of secant to the graph of f passing through the points (x, f(x)) e (x + h, f(x + h)) is given by the Newton’s quotient:

If the result takes positive values (negative), becoming closer to zero, it means that the sequence of points Qj is approaching the point P on the right (left). When

the derivative of f at the point, and is denoted by:
[2] [20] . If no such limit exists, we say that there is not the derivative of f(x) at the point. If the function has a
Figure 4. Graph of a f function at the P point with the tangent line that passes through P and the Qs secants approaching P.
derivative at a point, we say that f is derivable (or differentiable) at this point. Likewise, the equation can be
written as h represents a variation of x, such that:


Therefore, the Newton’s quotient is defined as the incremental ratio of f with respect to the variable x, at the point x [2] [20] .
4.3. Paraconsistent Differential Calculus
To establish a method of Paraconsistent Differential Calculus where contradictory values will not be despised it is considered initially the Newton’s quotient Equation (8) that can be written as:
It can be applied to the Newton’s quotient a K factor of normalization that aims to put its values within the limits of the PAL2v-Lattice τ, therefore:

where: K is a normalization Factor, whose action allows the equation to be done as the fundamentals of PAL2v.
With the normalization Factor in equation (10) are identified the degrees of Evidence of PAL2v annotation,
such that:


In Paraconsistent Logical Model the K value must be estimated so that the values of the degrees of Evidence become established within the fundamentals of PAL2v. For this becomes:



It is also possible to calculate by Equation (3) the Contradiction Degree of Newton’s quotient, such that:

In the Paraconsistent Logical Model the value of the K adjustment factor will define Contradiction Degree of the final Newton’s quotient, so its value will indicate where into PAL2v-Lattice τ will be the Paraconsistent Logical State (eτ), defined in the Equation (5).
4.4. Newton Normalization Factor
If in the point considered the maximum value of the function is





where:

KN is the Paraconsistent Newton Normalization Factor
The value of the Paraconsistent Derivative of the first-order in the physical world is obtained through reap- plying of Newton Normalization Factor (KN) in the result of Paraconsistent Newton’s quotient:

Thus, it is possible for the Paraconsistent Mathematics to be connected to the equilibrium point, defined by the Paraquantum Factor of quantization (hψ) of the PAL2v-Lattice τ [9] [12] [17] [19] .
The final value of Paraconsistent Derivative depends on the value of variation in x thus it depends on the in- crement of variable x chosen in the calculation.
4.5. Paraconsistent First-Order Derivative
It is verified that the location of the Paraconsistent logical State ε was adjusted in the PAL2v-Lattice τ through the Paraconsistent Newton Normalization Factor (KN) and identifies how it is represented any differentiable function



Newton’s quotient, which includes the Paraconsistent Newton Normalization Factor (KN), the analysis will be written as:

or

This normalization allows for the function



Thus, for the function

Similarly, the Equation (12) the Contradiction Degree of the Paraconsistent Newton’s quotient:

Therefore, the Paraconsistent values extracted from Newton’s quotient adjusted to Paraconsistent Logical Model depends of
Figure 5 shows the location of the Paraconsistent Logical state defined in the equilibrium point established by the Paraquantum Factor of quantization (hψ).
5. Examples of Resolution First-Order Paraconsistent Derivative
In this section it is presented examples of the use of the Paraconsistent Newton’s quotient in the resolution of first-order Derivative for different values of the Variable Increment x.
Example 1
It is wanted a final value of the first-order Paraconsistent Derivative of the function


Figure 5. Paraconsistent logical State adjusted in equilibrium point hψ through the Newton Normalization factor KN.
that the Contradiction Degree of the Newton’s quotient that is near the hψ, establishes thus a Paraconsistent Log- ical State ε of equilibrium of the PAL2v-Lattice τ.
Resolution: Initially, to form Paraconsistent Newton Normalization Factor it is calculated the maximum value of the function


It is calculated the value of the Paraconsistent Newton Normalization Factor, according to the Equation (13):
For an increment value of the variable x, for example,

The Paraconsistent Newton’s quotient is calculated according to Equations (15) or (16)
Recovering value of Paraconsistent Derivative in the physical world by Equation (14):
Therefore, for these conditions, where the increment of the variable x is



Decreasing to
The Certainty Degree of Paraconsistent Newton’s quotient calculated by Equation (17) is:
And the Paraconsistent Newton’s quotient calculated according to Equation (16) is:
Recovering the value of Paraconsistent Derivative in the physical world by Equation (14) becomes:
Therefore, for these conditions, where the increment of the variable x is



Decreasing the value of

The Paraconsistent Newton’s quotient is calculated according to Equation (16):
Recovering the value of Paraconsistent Derivative in the physical world by Equation (14):
Therefore, for these conditions, where the increment of the variable x is


Decreasing the value of
The Certainty Degree of Paraconsistent Newton’s quotient is calculated by Equation (17):
The Paraconsistent Newton’s quotient is calculated according to Equation (18):
Recovering the value of Paraconsistent Derivative in the physical world by Equation (14):
Therefore, for these conditions, where the increment of the variable x is



It is verified that the Contraction Degree of Paraconsistent Newton’s quotient obtained by Equation (18) ap- proaches to


For
For
For
For
Example 2
Through Paraconsistent Mathematics originated from the Paraconsistent Logical Model, determine:
1) The equation of the first-order Paraconsistent Derivative of the function
2) Using a value of the increment of the variable x of


Resolution
1) Using Paraconsistent Newton’s quotient placed in the form of Equation (15)



where:

KN is the Newton Normalization Factor, calculated by Equation (13), such that:
The Favorable Evidence Degree:
The Unfavorable Evidence Degree:
2) The first-order Paraconsistent Derivative of the function

a) Obtain the maximum value of the function at the point
b) Paraconsistent Newton Normalization Factor, will be:
c) Applying Equation (15) of Paraconsistent Newton’s quotient obtained in item a to

The value of the first-order Paraconsistent Derivative in the physical world is obtained by the Equation (14):
Therefore, for these conditions, where the increment of the variable x is




6. Conclusion
This paper presented a method for Differential Calculus using the foundations of Paraconsistent Logic applied to the Newton’s quotient. The adequacy of the Differential Calculus to the Paraconsistent Logical Model made the contradictions existing in the Differential Calculus be accepted as inherent to a model based on real situations, so an imperfect world. Thus, the Paraconsistent Differential Calculus, structured in a logic that accepts contradictions, is able to dissolve the uncertainties, aggregating values that conventionally would be discarded. Following the procedures of Paraconsistent Mathematics were presented some examples where results are obtained from resolutions of first-order Paraconsistent Derivative of some functions. The results indicate that Paraconsistent Mathematics for resolutions using first-order derivatives responds well to these basic applications and facilitates the computational treatment. In the second part of this work it will be studied the methods for using the Paraconsistent Logical Model applied to solving problems through second-order derivative.
References
- Stroyan, K.D., and Luxemburg, W.A.J. (1976) Introduction to the Theory of Infinitesimals. Academic Press, New York.
- Bell, J.L. (1998) A Primer of Infinitesimal Analysis. Cambridge University Press, Cambridge.
- Baron, M.E. (1969) The Origins of the Infinitesimal Calculus. Pergamon Press, Hungary.
- Keisler, H.J. (1976) Elementary Calculus: An Infinitesimal Approach. 1st Edition, Prindle, Weber & Schmidt, Boston.
- Kleene, S.C. (1952) Introduction to Metamathematics. North Holland/Van Nostrand, Amsterdam/New York.
- Da Silva Filho, J.I., Lambert-Torres, G. and Abe, J.M. (2010) Uncertainty Treatment Using Paraconsistent Logic: Introducing Paraconsistent Artificial Neural Networks. IOS Press, Amsterdam, 328.
- D’Ottaviano, I.M.G. and Carvalho, T.F. (2005) Da Costa’s Paraconsistent Differential Calculus and the Transference Theorem. 2nd Indian International Conference on Artificial Intelligence (II CAI-05), Pune, 1659-1678.
- Jas’kowski, S. (1969) Propositional Calculus for Contradictory Deductive Systems. Studia Logica, 24, 143-157. http://dx.doi.org/10.1007/BF02134311
- Da Silva Filho, J.I. (2011) Paraconsistent Annotated Logic in Analysis of Physical Systems: Introducing the Paraquantum hψ Factor of Quantization. Journal of Modern Physics, 2, 1397-1409. http://dx.doi.org/10.4236/jmp.2011.211172
- Da Costa, N.C.A. (1986) On Paraconsistent Set Theory. Logique et Analyse, 115, 361-371.
- Da Costa, N.C.A. (2000) Paraconsistent Mathematics. In: Batens, D., Mortensen, C., Priest, G., van Bendegen, J.P., Eds., Frontiers in Paraconsistent Logic: Proceedings. King’s College Publications, London, 165-179.
- Da Silva Filho, J.I. (2011) Paraconsistent Annotated Logic in Analysis of Physical Systems: Introducing the Paraquantum γψ Gamma Factor. Journal of Modern Physics, 2, 1455-1469. http://dx.doi.org/10.4236/jmp.2011.212180
- Arruda, A.I. (1989) Aspects of the Historical Development of Paraconsistent Logic. In: Priest, G., Routley, R. and Norman, J., Eds., Paraconsistent Logic: Essays on the Inconsistent, Philosophia Verlag, 99-130.
- Da Costa, N.C.A. (1974) On the Theory of Inconsistent Formal Systems. Notre Dame Journal of Formal Logic, 15, 497-510. http://dx.doi.org/10.1305/ndjfl/1093891487
- Krause, D. and Bueno, O. (2007) Scientific Theories, Models, and the Semantic Approach. Principia, 11, 187-201.
- Rogers, D.F. and Adams, J.A. (1990) Mathematical Elements for Computer Graphics. 2nd Edition, McGraw-Hill, New York.
- Da Silva Filho, J.I. (2012) Analysis of the Emissions Spectral line of the Paraquantum with Hydrogen Atom. Journal of Modern Physics, 3, 233-254. http://dx.doi.org/10.4236/jmp.2012.33033
- Da Silva Filho, J.I. (2012) An Introductory Study of the Hydrogen Atom with Paraquantum Logic. Journal of Modern Physics, 3, 312-333. http://dx.doi.org/10.4236/jmp.2012.34044
- Da Silva Filho, J.I. (2012) Study of the Interactions between Particles Based in Paraquantum Logic. Journal of Modern Physics, 3, 362-376. http://dx.doi.org/10.4236/jmp.2012.35051
- Pl Tipler, A. and Llewellyn, R.A. (2007) Modern Physics. 5th Edition, W. H. Freeman and Company, New York.
- Diethelm, K. and Ford, N. (2004) Multi-Order Fractional Differential Equations and Their Numerical Solution. Applied Mathematics and Computation, 154, 621-640. http://dx.doi.org/10.1016/S0096-3003(03)00739-2



















































