ABSTRACT

Received November 15, 2013; revised December 15, 2013; accepted December 23, 2013

We give a survey on the history, the main mathematical results and applications of the Mathematics of Harmony as a new interdisciplinary direction of modern science. In its origins, this direction goes back to Euclid’s “Ele- ments”. According to “Proclus hypothesis”, the main goal of Euclid was to create a full geometric theory of Pla- tonic solids, associated with the ancient conception of the “Universe Harmony”. We consider the main periods in the development of the “Mathematics of Harmony” and its main mathematical results: algorithmic measurement theory, number systems with irrational bases and their applications in computer science, the hyperbolic Fibo- nacci functions, following from Binet’s formulas, and the hyperbolic Fibonacci l-functions (λ = 1, 2, 3, ···), fol- lowing from Gazale’s formulas, and their applications for hyperbolic geometry, in particular, for the solution of Hilbert’s Fourth Problem.

Keywords:

Golden Ratio; Pascal’s Triangle and Fibonacci Numbers; Binet’s Formulas; Gazale’s Formulas; Hyperbolic Fibonacci Functions; Number Systems with Irrational Bases; Fibonacci l-Numbers; “Metallic Proportions”; Hilbert’s Fourth Problem

1. Introduction

In 2009, the International Publishing House “World Scientific” has published the book of Alexey Stakhov: “The Mathematics of Harmony―From Euclid to Contemporary Mathematics and Computer Science” [1] http://www.worldscientific.com/worldscibooks/10.1142/6635

The American philosopher Professor Scott Olsen, author of the excellent book: “The Golden Section: Na- ture’s Greatest Secret” [2] made a huge assistance in writing the book [1] and its preparation for the publication.

The publication of these books (see Figure 1) is a reflection of one of the most important trends in the devel- opment of modern science. The essence of this trend is very simple: a return to the “harmonic ideas” of Pytha- goras and Plato (the “golden ratio” and Platonic solids), embodied in Euclid’s “Elements” [3].

The newest discoveries in chemistry and crystallography: fullerenes, based on the “truncated icosahedron” (The Nobel Prize―1996), and quasi-crystals, based on the icosahedral or pentagonal symmetry (Nobel Prize― 2011), are brilliant examples, which confirm this trend.

The amount of such discoveries is increasing continuously. These include: “the law of structural harmony of systems” by Edward Soroko [4], based on the golden p-proportions, and the “law of spiral biosimmetry trans- formation” by Oleg Bodnar [5], based on the “golden” Fibonacci hyperbolic functions. It also includes a new theory of the genetic code, based on the “golden genomatrices” (author―Doctor of Physical and Mathematical Sciences Sergey Petoukhov, Moscow) [6]. These examples could go on.

Thus, the modern philosophy and theoretical natural sciences begun to use widely the “harmonic ideas” by

Pythagoras, Plato and Euclid. And we have every right to talk about the “revival” of ancient Greeks’ “harmonic ideas” in modern theoretical natural sciences. This fact puts forward a problem of the renaissance of these ancient harmonic ideas in modern mathematics. The publication of the book [1] is the answer of mathematics to this important trend.

The purpose of this article is to give a survey of the main stages, events and scientific findings, which led to the creation of “Mathematics of Harmony”, the new interdisciplinary direction of modern science.

2. The Mathematics of Harmony: The Opinion of Academician Yuri Mitropolsky

What is the Mathematics of Harmony”? What is its role in modern science and mathematics? The outstanding Ukrainian mathematician, the leader of the Ukrainian School of Mathematics, Honorary Director of the Institute of Mathematics of the Ukrainian Academy of Sciences and Editor-in Chief of the “Ukrainian Mathematical Journal” Academician Yuri Mitropolsky (Figure 2) wrote the following in his commentary [7]:

“One may wonder what place in the general theory of mathematics is occupied by Mathematics of Harmony created by Prof. Stakhov? It seems to me, that in the last centuries, as Nikolay Lobachevsky said, “mathematicians turned all their attention to the Advanced Parts of Analytics, neglecting the origins of Mathematics and not willing to dig the field that already been harvested by them and left behind.” As a result, this created a gap between “Elementary Mathematics” - basis of modern mathematical education, and “Advanced Mathematics”. In my opinion, the Mathematics of Harmony developed by Prof. Stakhov fills up that gap. I.e, “Mathematics of Harmony” is a big theoretical contribution, first of all to the development of “Elementary Mathematics” and as such should be considered of great importance for mathematical education.”

Thus, according to Mitropolsky, the Mathematics of Harmony is a new mathematical discipline, which fills the gap between the “Elementary Mathematics” and “Higher Mathematics”. That is, this new theory puts forward new challenges in the field of the “Elementary Mathematics”. In its origins, this theory goes back to the ancient mathematical topics: “Measurement Theory”, “Number Theory”, “Numeral Systems”, “Elementary Functions” and so on.

The main task of the “Mathematics of Harmony” is to find new mathematical results in the field of the “Elementary Mathematics” based on the “golden ratio” and Fibonacci numbers. It is proved a high efficiency of these results in such areas as theory of recurrence relations, theory of elementary functions, hyperbolic geometry, and finally, the computer and measuring engineering, coding theory [8-41].

3. About the Term of “The Mathematics of Harmony”

For the first time the term “the Mathematics of Harmony” was used in the article “Harmony of spheres”, placed in “The Oxford dictionary of philosophy” [42]:

“Harmony of spheres. A doctrine often traced to Pythagoras and fusing together mathematics, music, and

astronomy. In essence the heavenly bodies being large objects in motion, must produce music. The perfection of the celestial world requires that this music be harmonious, it is hidden from our ears only because it is always present. The mathematics of harmony was a central discovery of immense significance to the Pythagoreans.”

Thus, the concept of “the Mathematics of Harmony” is associated here with the “harmony of the spheres”, which is also called the “harmony of the world” (Latin “harmonica mundi”) or world music (Latin “musical mundane”). The harmony of the spheres is the ancient and medieval doctrine about the musical-mathematical construction of Cosmos, which goes back to the Pythagorean and Platonic philosophical tradition.

Another mention about “the Mathematics of Harmony”, as the ancient Greek great discovery, we find in the book by Vladimir Dimitrov “A new kind of social science. Study of self-organization of human dynamics” [43]. Let us consider the quote from the book:

“Harmony was a key concept of the Greeks, a conjunction of three strands of meaning. Its root meaning was aro, join, so harmonia was what joined. Another meaning was proportion, the balance of things that allowed an easy fit. The quality of joining and proportion then came to be seen in music and other arts.

The precondition for harmony for the Greeks was expressed in the phrase “nothing too much”. It also had a mysterious positive quality, which became the object of enquiry of their finest minds. Thinkers such as Pythago- ras sought to capture the mystery of harmony as something both inexpressible yet also illuminated by mathe- matics. The mathematics of harmony explored by the ancient Greeks is still an inspiring model for contempo- rary scientists. Crucial to it is their discovery of its quantitative expression in astonishing diversity and com-

plexity of nature through the golden mean (golden ratio), Ф (phi):, which is approximately equal to

1.618. It is described by Euclid in book five of his Elements: “A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to greater, so is greater to the less”.

Thus, in the book [43] the concept of “the Mathematics of Harmony” is directly associated with the “golden ratio”―the most important ancient mathematical discovery in the field of harmony, which at that time was called “the division of the segment in extreme and mean ratio”.

Finally, it is pertinent to mention that this term was used in Stakhov’s speech “The Golden Section and Modern Harmony Mathematics”, made at the 7th International Conference “Fibonacci Numbers and Their Applications” (Austria, Graz, 1996) [11].

4. The Most Important Periods in the Development of the Mathematics of Harmony

As mentioned above, very successful term of the “Mathematics of Harmony” was introduced to emphasize the most important feature of ancient Greek science (studying the Harmony of the Universe) [42,43]. The greatest interest in the “Harmony of Universe”, that is, in the ideas of Pythagoras, Plato and Euclid, always arose in the periods of greatest prosperity of the “human spirit”. From this point of view, the studying the “Mathematics of Harmony” can be divided into the following critical periods.

4.1. Ancient Greek Period

Conventionally, it can be assumed that this period starts with the research of Pythagoras and Plato. Euclidean’ “Elements” is a final event of this period. According to Proclus’ hypothesis [3], Euclid created his “Elements” in order to give a complete geometric theory of the five “Platonic solids,” which have been associated in the ancient Greek science with the “Harmony of the Universe”. Fundamentals of the theory Platonic solids (Figure 3) were placed by Euclid in the final Book (Book XIII) of his “Elements”.

In addition, Euclid simultaneously had introduced here some advanced achievements of ancient Greek mathematics, in particular, the “golden ratio” (Book II), which was used by Euclid for the creation of the geometric theory of “Platonic solids”.

4.2. The Middle Ages

In the Middle Ages it was made very important mathematical discovery. The famous Italian mathematician Leonardo of Pisa (Fibonacci) wrote a book “Liber Abaci” (1202). In this book, he described “the task of rabbits reproduction”. In solving this problem he introduced the remarkable numerical sequence―the Fibonacci numbers: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ··· which are given by the recurrence relation:

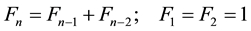(1)

The Fibonacci numbers can be extended to the negative values of the indices 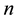(see Table 1).

In 17 c., the famous French astronomer Cassini had proved the following remarkable formula, which connects three neighboring Fibonacci numbers:

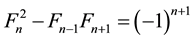(2)

4.3. The Renaissance

This period is connected with the names of the prominent figures of the Renaissance: Piero della Francesca (1412-1492), Leon Battista Alberti (1404-1472), Leonardo da Vinci (1452-1519), Luca Pacioli (1445-1517), Johannes Kepler (1571-1630). In that period two books, which were the best reflection of the idea of the “Universe Harmony,” were published. The first of them is the book “Divina Proprtione” (“The Divine Proportion”) (1509). This book had been written by the outstanding Italian mathematician and scholar monk Luca Pacioli under the direct influence of Leonardo da Vinci, who illustrated Pacioli’s book. The brilliant astronomer of 17th century Johannes Kepler made an enormous contribution to the development of the “harmonic ideas” of Pythagoras, Plato and Euclid.

In his first book Mysterium Cosmographicum (1596), he built the so-called “Cosmic Cup” (Figure 4)―an-

Figure 4. Kepler’s Cosmic Cup.

original model of the Solar system, based on the Platonic solids. The book Harmonice Mundi (Harmony of the Worlds) (1619) is the main Kepler’s contribution into the Doctrine of the Universe Harmony. In Harmony, he attempted to explain the proportions of the natural world―particularly the astronomical and astrological aspects―in terms of music. The central set of “harmonies” was the musica universalis or “music of the spheres”, which had been studied by Pythagoras, Ptolemy and many others before Kepler.

4.4. The 19th Century

This period is connected with the works of the French mathematicians Jacques Philip Marie Binet (1786-1856), Francois Edouard Anatole Lucas (1842-1891), German poet and philosopher Adolf Zeising (born in 1810) and the German mathematician Felix Klein (1849-1925).

Jacques Philip Marie Binet derived a mathematical formula to expresses the “extended” Fibonacci numbers

(see Table 1) through the “golden mean”:

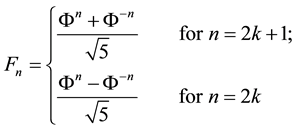(3)

where.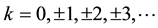

Francois Edouard Anatole Lucas introduced the Lucas numbers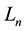, which are calculated by the same recurrence relation as the Fibonacci numbers (2), but with other seeds:

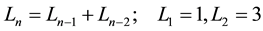(4)

Recurrence relation (4) generates the following numerical sequence:

(5)

The Lucas numbers (5) can be extended to the negative values of the indices (see Table 2).

The merit of Binet and Lukas is the fact that their researches became a launching pad for Fibonacci researches in the Soviet Union, the United States, Britain and other countries [44-46].

German poet Adolf Zeising in 1854 published the book “Neue Lehre von den Proportionen des menschlichen Körpers aus einem bisher unerkannt gebliebenen, die ganze Natur und Kunst durchdringenden morpholo- gischen Grundgesetze entwickelt”. The basic Zeising’s idea is to formulate the Law of proportionality. He for- mulated this Law as follows:

“A division of the whole into unequal parts is proportional, when the ratio between the parts is the same as the ratio of the bigger part to the whole, this ratio is equal to the golden mean.”

The famous German mathematician Felix Klein in 1984 published the book “Lectures on the icosahedron and the solution of equations of the fifth degree”, dedicated to the geometric theory of the icosahedron and its role in the general theory of mathematics. Klein treats the icosahedron as a mathematical object, which is a source for the five mathematical theories: geometry, Galois theory, group theory, invariant theory and differential equa- tions.

What is the significance of the ideas of the outstanding mathematician from the point of view of the Mathe- matics of Harmony [1]? According to Klein, the Platonic icosahedron, based on the “golden ratio,” is the main geometric figure of mathematics. It follows from this that the “golden ratio” is the main geometric object of mathematics, which, according to Klein, can unite all mathematics.

This idea of Felix Klein is consistent with the ideas of the article “Generalized Golden Sections and a new approach to geometric definition of a number,” published by the author in the “Ukrainian Mathematical Journal” [24]. This article presents the concept of the “golden” number theory, which can be the basis for the “golden” mathematics, based on the “golden ratio” and its generalizations.

4.5. The First Half of the 20th Century

In the first half of the 20th century the development of the “golden” paradigm of the ancient Greeks is associated with the names of the Russian Professor of architecture Grimm (1865-1942) and the classic of the Russian religious philosophy Paul Florensky (1882-1937).

In the theory of architecture, it is well-known the book “Proportionality in Architecture”, published by Prof. Grimm in 1935 [47]. The purpose of the book has been formulated in the “Introduction” as follows:

“In view of the exceptional significance of the Golden Section in the sense of the proportional division, which establishes a permanent connection between the whole and its parts and gives a constant ratio between them (which is unreachable by any other division), the scheme, based on it, is the main standard and is accepted by us in the future as a basis for checking the proportionality of historical monuments and modern buildings ··· Taking this general importance of the Golden Section in all aspects of architectural thought , the theory of proportio- nality, based on the proportional division of the whole into parts corresponding to the Golden Section, should be recognized as the architectural basis of proportionality at all.”

In the 20th years of 20th century, Pavel Florensky wrote the work “At the watershed of a thought.” Its third chapter is devoted to the “golden ratio”. The Belorussian philosopher Edward Soroko in the book [4] evaluates Florensky’s work as follows:

“The aim was to derive analytically the stability of the whole object, which is in the field of the effect of oppositely oriented forces. The project was conceived as an attempt to use the “golden ratio and its substantial basis, which manifests itself not only in a series of experimental observations of nature, but on the deeper levels of knowledge, for the case of penetration into the dialectic of movement, into the substance of things”.

4.6. The Second Half of the 20th Century and the 21st Century

In the second half of 20^th century, the interest in this area is increasing in all areas of science, including mathe- matics. The Soviet mathematician Nikolai Vorobyov (1925-1995) [44], the American mathematician Verner Hoggatt (1921-1981) [45], the English mathematician Stefan Vajda [46] and others became the most outstanding representatives of this trend in mathematics.

Reviving the idea of harmony in modern science is determined by new scientific realities. The penetration of the Platonic solids, the “golden ratio” and Fibonacci numbers in all areas of theoretical natural sciences (crys- tallography, chemistry, astronomy, earth science, quantum physics, botany, biology, geology, medicine, genetics, etc.), as well as in computer science and economics was the main reason for the renewed interest in the ancient idea of the Universe Harmony in modern science and the stimulus for the development of the “Mathematics of Harmony” [1-41].

4.7. The Article by Victor Shenyagin

Recently on the website “Academy of Trinitarizm, Institute of the Golden Section” has published the article by well-known Russian Fibonacci-scientist Victor Shenyagin [48] with the following appeal:

“Appeal to the international scientific community: On the appropriateness of nomination of Professor Stakhova AP to award the Abel Prize in Mathematics in 2014.”

Of course, it is pleasant for the author to get a high appreciation of his research from his colleagues. Similar estimations were given also by other well-known scientists: the Ukrainian mathematician academician Yuri Mi- tropolsky [7], the American philosopher Scott Olsen [49], the Belarusian philosopher Edward Soroko [50], the Russian philosopher Sergei Abachiev [51], and many others. Their feedback is the highest award for the author.

Unfortunately, this scientific discipline, called the “Mathematics of Harmony” [1] until now is not a generally recognized part of the conventional mathematics. However, this scientific direction became widely known in modern science after the publication of the book [1], as well as the author’s publications in the Ukrainian aca- demic and English scientific journals [3,8-41].

Let us consider the basic mathematical results and theories of the “Mathematics of Harmony,” mentioned by Victor Shenyagin in the article [48].

5. Algorithmic Measurement Theory

The algorithmic measurement theory is the first mathematical theory, created by the author during 70th years of 20 c. The foundations of this theory are described in the Stakhov’s books [12,13] (Figure 5).

Although this theory by its initial idea had purely applied character (“Synthesis of the optimal algorithms for analog-to-digital conversion”, by the way, this was the title of author’s doctoral dissertation, 1972), but in process of creating this theory, the author went out far for the application frameworks and touched the founda- tions of mathematics.

First of all, the author have excluded from consideration the abstraction of actual infinity as an internally con- tradictory concept (the “completed infinity”), because still Aristotle protested against this. As a result, the author has excluded from the algorithmic measurement theory Cantor’s axiom, which is the basis of the classical mea- surement theory, based on the continuity axioms. The author found the contradiction between Cantor’s axiom and the Archimedes’ axiom [12]. This contradiction implies automatically the contradictions in the foundations of mathematics. The famous Russian mathematician and philosopher Alexander Zenkin had developed these ideas in the article [52], where he criticizes Cantor’s theory of infinite sets.

Such a constructive approach to the algorithmic measurement theory, based on the abstraction of potential in- finity, allowed the author to solve the problem, which was never been considered in mathematics. We talk about the problem of the synthesis of optimal measurement algorithms, which are a generalization of well-known measurement algorithms: the “counting algorithm,” which lies at the basis of Euclidean definition of natural numbers, and the “binary algorithm,” which lies at the basis of the binary system, the basis of modern comput- ers.

Each measurement algorithm corresponds to some positional number system. From the algorithmic measure- ment theory, it follows all the known positional number systems. It is very important, that the new, unknown positional number systems, in particular, the “Fibonacci” and “binomial” number systems arose in the algorith- mic measurement theory [12].

Thus, the algorithmic measurement theory is a source for the new positional number systems. Note that ma-

thematics was never seriously engaged in number systems. The mathematics moved forward not very far in this area compared with the period of its origin. And this is the mistake of mathematics. New positional number sys- tems (in particular, introduced by the author Fibonacci p-codes) can become an alternative to the binary system for many critical applications.

6. Pascal’s Triangle and the Generalized Fibonacci Numbers

Pascal’s Triangle is so widely known and studied mathematical object that many mathematicians will be surprised what’s new can be found in this triangle? The book “Mathematical Discovery” (Russian translation, 1970) [53] by the American mathematician Polya is well-known. In this book Polya showed an unexpected connection of Pascal’s triangle with the Fibonacci numbers (see Figure 6).

The study of the so-called “diagonal sums” of Pascal’s triangle, conducted by many mathematicians (includ- ing the author of this article), has led to the discovery of an infinite amount of the recurrent sequences, called the Fibonacci p-numbers [12]. These recurrent sequences for the given are generated by the fol- lowing general recurrence relation:

for (6)

at the seeds:

. (7)

7. A Generalization of the “Golden Ratio”

By studying the Fibonacci p-numbers and considering the limit of the ratio of neighboring Fibonacci p-num-

bers, the author came to the following algebraic equation [12]:

(8)

The positive roots of the Equation (8) form a set of the new mathematical constants, which describe some algebraic properties of Pascal’s triangle. The classical “golden ratio” is a special case (p = 1) of the con- stants. On this basis, the constants have been called the “golden p-proportions”. This result has caused an admiration by academician Mitropolsky, who in his commentary [7] wrote the following:

“Let’s ponder upon this result. Within several millennia, starting since Pythagoras and Plato, the mankind used the widely known classical Golden Proportion as some unique number. And here in the end of the 20^th century the Ukrainian scientist Stakhov generalized this result and proved the existence of infinite number of the Golden Proportions! And all of them have the same right to express Harmony, as well as the classical Golden Proportion. Moreover, Stakhov proved, that the golden p-proportions represented a new class

of irrational numbers, which express some unknown mathematical properties of Pascal triangle. Clearly, such mathematical result is of fundamental importance for the development of modern science and mathematics.”

8. The Redundant Binary Positional Number Systems (the Fibonacci p-Codes)

Fibonacci measurement algorithms, based on the Fibonacci p-numbers [12], led to the discovery of the new po- sitional number systems, called the Fibonacci p-codes:

, (9)

where is a given integer; is the binary numeral of the ith digit; the Fibonacci p-number is the weight of the ith digit.

This expression is a generalization of the classical binary code (p = 0):

, (10)

which underlies the modern computers. For the case р > 0 all the Fibonacci р-codes are redundant positional binary systems, which can be used for the design of new computers (Fibonacci computers), which have super- high informational reliability.

9. Foreign Patents on the Fibonacci Computers

In 1976, the author worked during 2 months as Visiting-Professor of the Vienna University of Technology. At the final stage of the stay in Austria, the author made a speech “Algorithmic Measurement Theory and Foundations of Computer Arithmetic” at the joint meeting of the Austrian Computer and Cybernetics Societies. The success of the speech was stunning. It was recognized that this speech provides new informational and arithmetical foundation of computers.

This sudden interest of Austrian scientists in author’s speech became a reason of the letter of the Soviet Ambassador in Austria Ivan Yefremov, who sent it to the USSR State Committee for Science and Technology. On the basis of this letter, the Soviet State Invention Committee took the decision about the urgent patenting author’s inventions on “Fibonacci computers “abroad. 65 foreign patents of the U.S. Japan, England, France, Germany, Canada and other countries are official legal documents, which confirmed a priority of the author in this area.

10. Codes of the Golden Proportion

In 1957, the young (12 year old) American wunderkind George Bergman in one of the U.S. mathematical Journals had described the unique number system, called a number system with an irrational base [54]:

, (11)

where A is a some real number, is a binary numeral of the ith digit, is the

weight of the ith digit, is a base of “Bergman’s system (11). Unfortunately, the mathematicians of

20th century did not pay attention to this mathematical discovery, despite the fact that “Bergman’s system” (11) is the greatest contemporary mathematical discovery in the field of positional number systems after the discov- ery of the Babylonian positional principle of number representation and decimal and binary number systems.

In 1980, the author had generalized the number system (11) and introduced in mathematics a wide class of the positional number systems with irrational bases, called “codes of the golden p-proportions” [10]:

, (12)

where , is a binary numeral of the ith digit, is a base of the number system (12) (the golden р-proportion, following from Pascal’s triangle), is the weight of the ith di- git, connected with weights of the previous digits by the following identity:

. (13)

Theory of the codes of the golden p-proportions was set forth in the book [14]. This book attracted the attention of the Soviet scientific- popular Journal “Technology for young people”. In 1985, this Journal had published author’s article “Codes of the Golden Proportion, or the number systems for future computers?” [55]. This article was the “key” article of this Journal what had been emphasized by the collage “Codes of the Golden Proportion,” placed on the back cover of this Journal (see Figure 7).

The publication of author’s article in the famous scientific-popular Journal by circulation of 1.7 million copies caused a big interest of scientific community in this research direction, which has became well known not only in the USSR but also abroad.

Note that the expression (12) includes an infinite number of the positional binary number systems, because every generates its own number system. In particular, for the case the base and the code of the golden p-proportion (12) are reduced to the classical binary system, and for the case to Bergman’s system (11).

11. The “Golden” Number Theory

Academician Yuri Mitropolsky, Сhief-Editor of the “Ukrainian Mathematical Journal”, has invited the author to submit the article on the codes of the golden p-proportions for the Journal. In 2004, according to Mitropolsky’s recommendation, the article “The generalized golden proportions and a new approach to geometric definition of a number” was published in this prestigious mathematical Journal [24].

The main idea of the article is reduced to the following. The codes of the golden p-proportions, which are connected with Pascal’s triangle, can be considered as the beginning of the new number theory, the “golden” number theory. Indeed, with the help of the codes of the golden p-proportions we can represent all real numbers, including natural, rational and irrational. The codes of the golden p-proportions change our ideas about the relationship between rational and irrational numbers, because the special irrational numbers (the golden p-proportions) are becoming the basis of all numbers and, therefore, of all mathematics.

Consider one unusual result of the “golden” number theory on the example of the Bergman’s system (11). For this, we represent the natural number N in the Bergman’s system (11):

. (14)

It is proved [24] that the sum of (14) for any natural number N is finite always, that is, any natural number N can be represented as the finite sum of the powers of the “golden proportion”. Since all powers of the “golden proportion” are irrational numbers (except for), then this assertion is far from trivial.

Let us consider the so-called “extended” Fibonacci numbers (see Table 1).

We substitute now the “extended” Fibonacci numbers instead the powers into the expression (14). To our surprise, we find [24] that this sum is equal to 0 for any natural number N, that is,

. (15)

This property has been called the Z-property of natural numbers [24]. Since this property is valid only for

natural numbers, this means that in [24] we found a new property of natural numbers, via 2.5 thousand years of their theoretical study (academician Mitropolsky was thrilled!).

12. Proclus Hypothesis: A New View on Euclid’s “Elements” and the History of Mathematics

“Proclus hypothesis,” formulated in the 5th century AD by the famous Greek philosopher and mathematician Proclus Diadochus (412 - 485), contains the unexpected view on Euclid’s “Elements”.

According to Proclus, Euclid’s goal was not to set forth the geometry itself, but to build a complete theory of regular polyhedra (“Platonic solids”). This theory was set forth by Euclid in the XIII-th, that is, the final book of the “Elements” what in itself is an indirect confirmation of the “Proclus hypothesis”.

To solve this problem, Euclid had included the necessary mathematical information into the “Elements.” The most curious thing is that he had introduced in the Book II the “golden section,” used by him for the creation of geometric theory of the dodecahedron. In Plato’s Cosmology, the regular polyhedra had been associated with the “Harmony of the Universe”. This means, that Euclid’s “Elements” are based on the “harmonic ideas” of Pythagoras and Plato, that is, Euclid’s “Elements” are historically first variant of the “Mathematics of Harmony”. This unexpected view on the “Elements” leads to the conclusion, which changes our view on the history and structure of mathematics.

As is known, the famous Russian mathematician academician Kolmogorov in the book [56] had identified the two main, that is, “key” problems, which stimulated the development of mathematics at the stage of its origins: the “counting problem” and the measurement problem. However, it follows from “Proclus hypothesis” another “key” problem: the “harmony problem,” which underlies Euclid’s “Elements”.

We can see that three “key” problems―the counting problem, the measurement problem, and the harmony problem―underlie the origins of mathematics (see Figure 8).

The first two “key” problems resulted in the creation of two fundamental notions of mathematics―natural number and irrational number that underlie the Classical Mathematics. The harmony problem, connected with the division in extreme and mean ratio (the “golden ratio”) (Proposal II.11 of Euclid’s Elements) resulted to the Harmony Mathematics [1]―a new interdisciplinary direction of contemporary science and mathematics.

This approach leads to the conclusion, which is a surprise for many mathematicians. It is found, in parallel with the Classical Mathematics, one more mathematical direction―the Harmony Mathematics―had been developing in ancient science. Similarly to the Classical Mathematics, the Harmony Mathematics has its origin in Euclid’s Elements. However, the Classical Mathematics focuses on the axiomatic approach, while the Harmony Mathematics is based on the golden section (Proposal II.11) and Platonic Solids described in Book XIII of Euclid’s Elements. Thus, Euclid’s Elements is a source of the two independent mathematical directions: the Classical Mathematics and the Harmony Mathematics.

For many centuries, the main focus of mathematicians was on the creation of the Classical Mathematics, which became the Czarina of Natural Sciences. However, the forces of many prominent mathematicians and thinkers―since Pythagoras, Plato and Euclid, Pacioli, Kepler up to Lucas, Binet, Vorobyov, Hoggatt and so

forth―were directed towards the development of the basic concepts and applications of the Harmony Mathe- matics. Unfortunately, these important mathematical directions had been developing separately from one other. The time has come to unite the Classical Mathematics and Harmony Mathematics. This unusual union can lead to new scientific discoveries in mathematics and natural sciences.

A new approach to the mathematics origin (see Figure 8) is very important for school mathematical education. This approach introduces, by very natural manner, the idea of harmony and the golden section into school ma- thematical education. This provides pupils an access to ancient science and to its main achievement―the har- monic ideas―and to tell them about the most important architectural and sculptural works of the ancient art based upon the golden section (including pyramid of Khufu (Cheops), Nefertiti, Parthenon, Doryphorus, Venus and so on).

13. Hyperbolic Fibonacci Functions and “Bodnar’s Geometry”

13.1. Classical Hyperbolic Functions

Hyperbolic functions were introduced by the Italian mathematician Vincenzo Riccati in 1757. He first introduced the notation sh and ch. Further investigations of hyperbolic functions were made by Lambert. Hyperbolic functions have the following form:

(16)

The formulas (16) allow us to prove a number of important identities for hyperbolic functions, such as:

(17)

The interest in the hyperbolic functions in mathematics and theoretical physics has increased dramatically in the 19th century, when the Russian mathematician Nikolai Lobachevsky developed a new type of geometry, based on the hyperbolic functions, and therefore called hyperbolic geometry.

13.2. Hyperbolic Fibonacci Functions

There is an analogy between the hyperbolic functions (16) and Binet’s formulas (3), introduced in 19 century. By using this analogy, the Ukrainian mathematicians Alexey Stakhov, Ivan Tkachenko and Boris Rozin have introduced a new class of the hyperbolic functions called hyperbolic Fibonacci functions [17,21].

Hyperbolic Fibonacci sine

(18)

Hyperbolic Fibonacci cosine

(19)

These functions retain, on the one hand, all the known properties of the classical hyperbolic functions (16). In particular, the identity (17) looks as follows:

. (20)

However, the uniqueness of the hyperbolic Fibonacci functions (18), (19) consists in the fact that they have recursive property, similar to the properties of the Fibonacci numbers. Moreover, the “extended” Fibonacci numbers (Table 1), given by Binet’s formulas (3), are connected with the hyperbolic Fibonacci functions (18), (19) by the following simple relation:

(21)

This unique property of the functions (18), (19) is demonstrated on the graphs in Figure 9.

Here the graphs of the hyperbolic sine and the hyperbolic cosine are represented.

The points on the graph correspond to the extended Fibonacci numbers with the even indexes:

. (22)

The points on the graph correspond to the extended Fibonacci numbers with the odd indexes:

(23)

13.3. Bodnar’s Geometry

Note that the relations (21)-(23) are explaining why the “Fibonacci spirals” appear at the surface of phyllotaxis objects (pine cones, cacti , pineapples, sunflower heads, etc.). This is proved by the Ukrainian researcher Oleg Bodnar in his amazing geometric theory of phyllotaxis, the most common botanical phenomenon. “Bodnar’s geometry” [5] shows that the “world of phyllotaxis” is obeying to the laws of the special hyperbolic geometry, which is described by mathematical relationships based on the hyperbolic Fibonacci functions (18) and (19).

“Bodnar’s geometry” shows that hyperbolic geometry is much more common in nature than previously assumed. Substantially all wildlife is the epitome of a special type of hyperbolic geometry - “Bodnar’s geometry,” which uses a special class of hyperbolic functions - hyperbolic Fibonacci functions.

It is this view on the “phyllotaxis geometry” gives us a right to claim that the hyperbolic Fibonacci functions (18) and (19) [17,21] and “Bodnar’s geometry” [5] are the fundamental discoveries of modern science.

14. Fibonacci l-Numbers, the Generalized Cassini Formula and the “Metallic Means”

14.1. Fibonacci λ-Numbers

In the end of 20th c. and the beginning of 21 c. the Fibonacci numbers theory [44-46] has been supplemented with the new mathematical results, based on the Fibonacci λ-numbers and the “metallic proportions” [57-63].

Let us give a natural number and consider the following recursive relation:

(24)

The recursive relation (24) “generates” an infinite number of the new numerical sequences, because every number l “generates” its own numerical sequence (24).

For the case the recursive relation (24) is reduced to the following recursive relation:

. (25)

This recursive relation “generates” the classic Fibonacci numbers:

. (26)

Based on this fact, we will name the numerical sequences, generated by the recursive relation (24), the

Fibonacci l-numbers. Note, that Fibonacci l-numbers are a partial case of the Lucas sequences, introduced in 19^th century by the famous French mathematician Eduardo Lucas [64].

For the case the recursive relation (24) is reduced to the recursive relation

, (27)

which “generates” Pell numbers:

(28)

14.2. A Generalization of Cassini’s Formula for the Fibonacci l-Numbers

The Fibonacci l-numbers have many remarkable properties, similar to the properties of the classic Fibonacci numbers. It is proved that the Fibonacci l-numbers, as well as the classical Fibonacci numbers, can be “expanded” to the negative values of the discrete variable n.

Table 3 shows the four “extended” sequences for the Fibonacci l-numbers, corresponding to the values.

It is proved in [36] that Cassini’s formula (2) can be generalized for the case of the Fibonacci l-numbers. The generalized Cassini formula has the following form [36]:

(29)

The most curious thing is that the mathematical result (29) may become as a surprise not only for the “lovers of mathematics,” but also for the professional mathematicians specializing in number theory. The Fibonacci l-numbers are a new set of integers (what is the subject of study for number theory) with unique mathematical property (29). This means that within the “mathematics of harmony” [36] a new fundamental mathematical result was obtained. This result has a direct relation to number theory, the oldest mathematical discipline.

14.3. The “Metallic Means”

If we take the ratio of the two adjacent Fibonacci l-numbers and direct the index n to infinity, we

get the following result:

, (30)

where is a positive root of the following algebraic equation:

. (31)

The root has the following form:

. (32)

Note that for the case the formula (32) is reduced to the classical “golden ratio”. This

means that the formula (32) gives an infinite number of new mathematical constants called “metallic means” or “metallic proportions” by the Argentinean mathematician Vera W. de Spinadel [57].

If we take in (32), then we get the following mathematical constants, having the following names (according to Vera de Spinadel [57]):

It is clear that the number of the “metallic proportions” (32) is theoretically infinite. The most significant is the fact that for the case l=1 the formula (32) is reduced to the classical “golden ratio.” This means that the “metallic proportions” like the “golden ratio” may express some new kinds of “mathematical harmony,” which can actually exist in Nature.

15. Gazale’s Formulas and Hyperbolic Fibonacci l-Functions

15.1. Gazale’s Formulas

The formulas (24) give the Fibonacci l-numbers recursively. However, the Fibonacci l-numbers can be represented in analytical form through the “metallic proportions” (32). Such formulas have been deduced by the French mathematician Midhat Gazale [58]:

(33)

where.

Gazale’s formulas (23) are a generalization of Binet’s formulas (3). A distinctive feature of (33) is that they generate an infinite number of the formulas (33), because each natural number corresponds to the different Gazale’s formulas (33). In particular, for the case l = 1 Gazale’s formulas (33) are reduced to Binet’s formulas (3).

15.2. Hyperbolic Fibonacci l-Functions

Gazale’s formulas (33) became a source for the introduction of the hyperbolic Fibonacci l-functions [34,37].

Hyperbolic Fibonacci l-sine

(34)

Hyperbolic Fibonacci l-cosine

(35)

It is proved [34,37] that the hyperbolic Fibonacci l-functions (34), (35) coincide with the “extended” Fibonacci l-numbers, given by Gazale’s formulas (33), for the discrete values of the variable x = n = 0, ±1, ±2, ±3, …, that is,

. (36)

It is proved [34,37], that the functions (34) and (35) retain all the known properties of the classic hyperbolic functions (3). For example, the well-known property (17) for the case (34) and (35) takes the following form:

. (37)

Note that the hyperbolic functions (34) and (35) are reduced to the hyperbolic Fibonacci functions (18) and (19) for the case. For this case, the formula (37) is reduced to the formula (20).

However, a number of the hyperbolic functions, given by (34) and (35), is theoretically infinite because every natural number l = 1, 2, 3,・・・” generates” its own variant of the hyperbolic functions of the kind (34) and (35).

16. Hilbert’s Fourth Problem and a New Challenge to Theoretical Natural Sciences

16.1. Hilbert’s Problems

In his 23 mathematical problems [65], the famous mathematician David Hilbert (See Figure 10) could not ignore the mathematical problems related to the non-Euclidean geometry. He considered the hyperbolic geometry (Lobachevski’s geometry) and elliptic geometry (Riemann geometry) as the geometries closest to the Euclidean geometry. Hilbert’s Fourth Problem [65,66], which relates to the non-Euclidean geometry, was formulated by him as follows [67]:

“The more general question now arises: Whether from other suggestive standpoints geometries may not be devised which, with equal right, stand next to Euclidean geometry.”

Hilbert’s citation contains the formulation of a very important scientific problem, which is of fundamental interest not only for mathematics, but also for all theoretical natural sciences: are there non-Euclidean geometries, which are close to the Euclidean geometry and are interesting from the “other suggestive standpoints?” If we consider it in the context of theoretical natural sciences, then Hilbert’s Fourth Problem is about finding NEW HYPERBOLIC WORLDS OF NATURE, which are close to the Euclidean geometry and reflect some new properties of Nature’s structures and phenomena.

Unfortunately, the attempts at solving Hilbert’s Fourth Problem, made by German mathematician Herbert Hamel (1901) and later by the Soviet mathematician Alexey Pogorelov [68] (1974), have not led to significant progress, as described in Wikipedia’s articles “Hilbert problems” [65] and the “Fourth Hilbert problem” [66]. In these articles, the status of the problem is formulated as “too vague to be stated resolved or not” and Pogorelov’s solution even is not mentioned. About the same point of view on Hilbert’s Fourth Problem is presented in the remarkable book [69]. So, Wikipedia’s mathematical community lays the blame for the fact why Hilbert’s Fourth Problem is not resolved until now, on David Hilbert, who formulated this problem not clearly enough.

16.2. From the “Game of Postulates” to the “Game of Functions”

According to [41], the reason lies elsewhere. All the known attempts to solve this problem (Hamel, Pogorelov) were in the traditional framework; let’s call this the “game of postulates.” This “game” started from the works by Gauss, Lobachevski and Bolyai, when Euclid’s 5th postulate was replaced by the opposite one. This was the most major step in the development of the non-Euclidean geometry, called “Lobachevski’s geometry.” The geometry, which changed the traditional geometric representations, is also known as “hyperbolic geometry.” This name highlights the fact that this geometry is based on the hyperbolic functions (16).

It is important to emphasize that the very name of “hyperbolic geometry” contains another way for the solu- tion of Hilbert’s Fourth Problem: searching for the new classes of “hyperbolic functions,” which can be the basis for other hyperbolic geometries. Every new class of the hyperbolic functions generates its own new variant of the “hyperbolic geometry.” By analogy with the “game of postulates” this way to solve Hilbert’s Fourth Prob- lem can be named the “game of functions” [41].

16.3. The Essence of the New Original Solution of Hilbert’s Fourth Problem

With the solution of Hilbert’s Fourth Problem, described in [37-40], the system of axioms of hyperbolic geometry remains unchanged. But the kind of hyperbolic functions, which describe the basic relationships of hyperbolic geometry, has changed. We use the new classes of the hyperbolic functions―the hyperbolic Fibonacci functions (18) and (19) with the unique mathematical property (21) and the hyperbolic Fibonacci l-functions (34) and (35) with the unique mathematical property (36).

As is known, the classic metric form of Lobachevski’s plane with pseudo-spherical coordinates which has a Gaussian curvature, is given with the following formula [37-40]:

, (38)

where is an element of length, is a classic hyperbolic sine from (16). It is clear that the classical hyperbolic sine plays a key role in the metric form of Lobachevski’s plane (38).

Developing the idea of metric form of Lobachevski’s plane (38), the following formula for the metric form of Lobachevski’s plane, based on the hyperbolic Fibonacci l-functions (34) and (35), has been derived in [37-40]:

, (39)

where is the “metallic proportion” (32) and is the hyperbolic Fibonacci l-sine

(44). The forms (39) are called the metric l-forms of Lobachevski’s plane [25,26].

This formula gives an infinite number of new “Lobachevsky’s geometries” (“golden,” “silver,” “bronze,” “copper” and so on to infinity).

Thus, the formula (39) sets an infinite number of the metric forms of Lobachevski’s plane. This means that there is infinite number of Lobachevski’s geometries, which are based on the “metallic proportions” (32). These new Lobachevski’s geometries “with equal right, stand next to Euclidean geometry” (David Hilbert). Thus, the formula (39) can be considered as the partial original solution of Hilbert’s Fourth Problem. There is an infinite number of Lobachevski’s geometries, described by the formula (39), which are close to Euclidean geometry. Every of these geometries manifest itself in Fibonacci l-numbers (24), which can appear in physical world similarly to “Bodnar’s geometry”, where the classical Fibonacci numbers appear at the surface of phyllotaxis objects.

16.4. A New Challenge for Theoretical Natural Sciences

Thus, the main result of the research, described in [37-40], is a proof of the existence of an infinite number of hyperbolic functions (34) and (35), based on the “metallic proportions” (32). In addition, each class of hyperbolic functions, corresponding to (34) and (35), “generates” for the given its own “hyperbolic geometry,” which leads to the appearance in the “physical world” with specific properties, which depend on the “metallic proportions” (32). The new geometric theory of phyllotaxis, created by Oleg Bodnar [5], is a striking example of this. Bodnar proved that “the world of phyllotaxis” is a specific “hyperbolic world,” in which the “hyperbolicity” manifests itself in the “Fibonacci spirals” on the surface of “phyllotaxis objects”.

However, the hyperbolic Fibonacci functions (18) and (19), which underlie the “hyperbolic phyllotaxis world,” are a special case of the hyperbolic Fibonacci l-functions (34) and (35). In this regard, there is every reason to sup- pose that other types of hyperbolic functions (34) and (34) can be the basis for modeling of new “hyperbolic worlds” that can really exist in Nature. Modern science cannot find these special “hyperbolic worlds”, because hyperbolic functions (34) and (35) were unknown for it. Basing on the success of “Bodnar’s geometry” [5], one can put forward in front to theoretical physics, chemistry, crystallography, botany, biology, and other branches of theoretical natural sciences the challenge to find new “hyperbolic Nature’s worlds”, based on other classes of hyperbolic functions given by (34) and (35).

17. Fibonacci and “Golden” Matrices

17.1. Fibonacci Q-Matrices

The Fibonacci Q-matrix [45]

(40)

is a generating matrix for the Fibonacci numbers and has the following wonderful properties:

(41)

. (42)

Note that there is a direct relation between the Cassini formula (2) and the formula (42), which gives the de- terminant of the matrix (41).

17.2. Fibonacci Q_p-Matrices

The article [18] introduces a generating matrix for the Fibonacci p-numbers. It is called the Q_p-matrix:

. (43)

The following properties of the Q_p-matrix (43) are proved in [18]:

(44)

, (45)

where; and

17.3. The “Golden” Matrices

In [33] a special class of the square matrices called the “golden” matrices was introduced. Their peculiarity is the fact that the hyperbolic Fibonacci functions (18) and (19) are elements of these matrices:

(46)

If we calculate the determinants of the matrices (46), we obtain the following unusual identities:

. (47)

18. A New Theory of Redundant Coding Based on the Fibonacci Matrices

Let’s consider the following coding/decoding method described in [30] and represented in Table 4. Represent the initial message in the form of the square (p + 1) ´ (p + 1)-matrix M with determinant and use for its coding the direct Fibonacci Q_p-matrix of the same size and for the decoding the inverse matrix according to Table 4.

It follows from Table 4 that for the given p (p = 0, 1, 2, 3, ···) the Fibonacci coding consists in the multiplication of the initial (p + 1) ´ (p + 1)-matrix M by the coding matrix given by (44). The code matrix E is a result of such matrix multiplication. Then the Fibonacci decoding consists in the multiplication of the code matrix E by the “inverse” matrix. Note that the coding/decoding method is trivial for the case p = 0. However, the coding/decoding methods, corresponding to the cases p>0, represent by themselves some code transformations of the initial message M to the code matrix E and this transformation is useful for some applications.

Error detection and correction is based on the following relation, which connects the determinant of the code matrix and the determinant of the coding matrix:

. (48)

Note that the coding/decoding method, given by Table 4, ensure infinite variants of the Fibonacci coding/decoding, because every Fibonacci coding matrix and its inverse matrix (;) “generate” their own Fibonacci coding/decoding method.

A new error-correcting theory based on the Fibonacci Q_p-matrices [30] has the following advantages in comparison to the algebraic error-correcting codes:

1) The Fibonacci coding/decoding method is reduced to matrix multiplication, that is, to the well-known algebraic operation, which is realized very well in modern computers.

2) The main practical peculiarity of the coding method is the fact that large information units, in particular, matrix elements, are objects of error detection and correction.

3) The simplest Fibonacci coding/decoding method (p = 1) can guarantee the restoration of all “erroneous” code (2 ´ 2)-matrices having “single”, “double” and “triple” errors.

4) The potential correction ability of the method for the simplest case p = 1 i exceeds essentially the potential correction ability of all well-known algebraic error-correcting codes. This means that the new coding theory based on matrix approach [30] is of great practical importance for modern computer science.

19. The “Golden” Ternary Mirror-Symmetrical Arithmetic

For the first time, the “golden” ternary mirror-symmetrical arithmetic was described in the article “Brousentsov’s ternary principle, Bergman’s number system and ternary mirror-symmetrical arithmetic”, published in “The Computer Journal” in 2002 [19]. The article caused a positive reaction from the Western computer com- munity. The prominent American mathematician Donald Ervin Knuth (see Figure 11) congratulated the author

with the publication of the article [19]. In his letter, he informed the author about his intention to include a de- scription of the “golden” mirror-symmetrical arithmetic into the new edition of the book “Art of Computer Pro- gramming”.

Why the article [19] caused the interest of Donald Knuth? It is proved in [19] that any integer N (positive or negative) may be represented as follows:

, (49)

where is a ternary numeral, is the weight of the ith digit, is the golden propor-

tion.

Note that the base of the number system (49) is the square of the “golden ratio,” that is,

. (50)

This means that the number system (49) belongs to the category of the number systems with irrational bases.

The abridged ternary digital record of the number system (49) has the following form:

. (51)

It is proved in [19], that the ternary digital record (51) for any integer N consists of two parts, the left hand part and right hand part, symmetrically located relatively to the 0^th digit.

Table 5 presents the ternary digital records of the initial natural numbers in the number system (49). As fol- lows from Table 5, all ternary records of positive integers have the property of the so-called “mirror symmetry.” The essence of this property is that the left part of the ternary code (51) is a mirror reflection of the right part; in this connection,. It is proved in [19] that all integers (positive and negative) have the property of “mirror symmetry” at their representation in the ternary number system (49). That is why, the ternary system (49) is named in [19] the ternary mirror-symmetrical number system.

We note one more unusual property of the ternary mirror-symmetrical number system (49). In traditional po- sitional number systems (decimal, binary), the increase of a number is realised by the extension of digital re- cording in the direction of the higher digits. As follows from Table 5, for the case of the mirror-symmetrical ternary recording (51), the extension of ternary digital recording is realized by the extension of the ternary digi- tal recording mirror-symmetrically to the left and to the right simultaneously.

It is proved in [19] that the property of “mirror symmetry” remains valid at the realization of arithmetical op- erations, that is, the results of these operations are always represented in the mirror-symmetric form. This means

that this property can be used in computers to control the arithmetical operations.

20. International Congress on Mathematics of Harmony

This Congress was held in October 2010 at Mechnikov’s Odessa National University (Ukraine). https://sites.google.com/site/harmonymathkongress/. This Congress gathered together leading experts in the field of the “golden ratio,” Fibonacci numbers and their applications not only from Ukraine, Russia, Belarus, but also from other countries and continents (USA, Germany , Chile, South Africa) (see Figure 12).

Point 7 of the Congress Resolution claims the following:

“The publication of the book AP Stakhov “The Mathematics of Harmony. From Euclid to Contemporary Mathematics and Computer Science “(World Scientific, 2009) is one of the most important events in this area. The book is the result of author’s 40-year research in this area. Stakhov’s book gained a widespread international recognition. One of the leading U.S. experts in the field of harmony and the “golden section” Prof. Scott Olsen wrote in his review: “Stakhov’s ideas Stakhova so significant that his new book may well change not only the consideration of the history of mathematics, but also the future development of mathematics in its applications to theoretical natural sciences.”

21. Conclusions

The following conclusions follow from this study:

1) The first conclusion touches on the question of the origin of mathematics and its development. This conclusion can be unexpected for many mathematicians. We assert that since the Greek period, the two mathematical doctrines―the Classical Mathematics and the Harmony Mathematics―begun to develop in parallel and independent one another. They both originated from one and the same source―Euclid’s Elements, the greatest mathematical work of the Greek mathematics. Geometric axioms, the beginnings of algebra, theory of numbers, theory of irrationals and other achievements of the Greek mathematics were borrowed from Euclid’s Elements by the Classical Mathematics. On the other hand, a problem of division in extreme and mean ratio (Theorem II.11) called later the golden ratio, and a geometric theory of regular polyhedrons (Book XIII), expressing the Harmony of the Cosmos in Plato’s Cosmology, were borrowed from Euclid’s Elements by the Mathematics of Harmony. We affirm that Euclid’s Elements were the first attempt to reflect in mathematics the main scientific idea of the Greek science, the idea of Harmony. According to Proclus, the creation of geometric theory of Platonic Solids (Book XIII of Euclid’s Elements) was the main purpose of Euclid’s Elements.

2) The second conclusion touches on the development of number theory. We affirm that new constructive definitions of real numbers, based on Bergman’s system (11) and the codes of the golden p-proportions (12), overturn our ideas about relationship between rational and irrational numbers [3]. A special class of irrational numbers―the golden ratio and golden p-proportions, following from Pascal’s triangle, becomes a base of new number theory―the “golden” number theory [24], because all rest of real numbers can be reduced to them by using the definitions (11) and (12). New property of natural numbers Z-property (15), following from this ap- proach, is a confirmation of a fruitfulness of this approach [24].

3) The third conclusion touches on the development of hyperbolic geometry. We affirm that a new class of hyperbolic functions, the hyperbolic Fibonacci functions (18) and (19) [17,21] and the hyperbolic Fibonacci - functions (34) and (35) [34,37], can become inexhaustible source for the development of hyperbolic geometry. We affirm that the formulas (34) and (35) give an infinite number of hyperbolic functions similar to the classical hyperbolic functions, which underlie Lobachevski’s geometry. This affirmation can be referred to one of the main mathematical results of the Mathematics of Harmony. The original solution of Hilbert’s Fourth Problem [37-41] confirms a fruitfulness of this approach to hyperbolic geometry.

4) The fourth conclusion touches on the applications of the Mathematics of Harmony in computer science. We affirm that the Mathematics of Harmony is a source for the development of new information technology― the “Golden” Information Technology based on the Fibonacci p-codes (9), Bergman’s system (11), codes of the golden p-proportions (12), and “golden” ternary mirror-symmetrical arithmetic [19].

5) The fifth conclusion touches on the applications of the Mathematics of Harmony in modern mathematical education. We affirm that the Mathematics of Harmony should become a base for the reform of modern mathematical education on the base of the ancient idea of Harmony and golden section. Such an approach can increase an interest of pupils in studying mathematics because this approach brings mathematics and natural sci- ences together. A study of mathematics turns into fascinating search of new mathematical regularities of Nature.

6) The sixth conclusion touches on the general role of the Mathematics of Harmony in the progress of contemporary mathematics. We affirm that the Mathematics of Harmony can overcome a contemporary crisis in the development of the 20th century mathematics that resulted in the weakening of the relationship between mathematics and theoretical natural sciences [70]. The Mathematics of Harmony is a true “Mathematics of Nature” incarnated in many wonderful structures of Nature (pine cones, pineapples, cacti, heads of sunflowers and so on), and it can give birth to new scientific discoveries. A new geometric theory of phyllotaxis (“Bodnar’s geometry”) [5] is a brilliant confirmation of this fact.

Acknowledgements

The author would like to express acknowledgements to Professor Scott Olsen (U.S.) for the English edition of this article and valuable remarks.

References