Applied Mathematics
Vol.5 No.4(2014), Article ID:43570,5 pages DOI:10.4236/am.2014.54061
Further Results about Calibration of Longevity Risk for the Insurance Business
Mariarosaria Coppola1, Valeria D’Amato2
1Department of Political Sciences, Federico II University, Naples, Italy
2Department of Statistics and Economics, Campus di Fisciano, University of Salerno, Salerno, Italy
Email: m.coppola@unina.it, vdamato@unisa.it
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 23 September 2013; revised 23 October 2013; accepted 7 November 2013
ABSTRACT
In life insurance business, longevity risk, i.e. the risk that the insured population lives longer than the expected, represents the heart of the risk assessment, having significant impact in terms of solvency capital requirements (SCRs) needed to front the firm obligations. The credit crisis has shown that systemic risk as longevity risk is relevant and that for many insurers it is actually the dominant risk. With the adoption of the Solvency II directive, a new area for insurance in terms of solvency regulation has been opened up. The international guidelines prescribe a market consistent valuation of balance sheets, where the solvency capital requirements to be set aside are calculated according to a modular structure. By mapping the main risk affecting the insurance portfolio, the capital amount able to cover the liabilities corresponds to each measured risk. In Solvency II, the longevity risk is included into underwriting risk module. In particular, the rules propose that companies use a standard model for measuring the SCRs. Nevertheless, the legislation under consideration allows designing tailor-made internal models. As regards the longevity risk assessment, the regulatory standard model leads to noteworthy inconsistencies. In this paper, we propose a stochastic volatility model combined with a so-called coherent risk measure as the expected shortfall for measuring the SCRs according to more realistic assumptions on future evolution of longevity trend. Finally empirical evidence is provided.
Keywords: Solvency II; Solvency Capital Requirement; Longevity Risk; Longevity Shocks; Expected Shortfall

1. Introduction
The analysis and understanding of longevity risk, i.e. the unexpected improvement in the future longevity trend, has only recently been examined crucial for insurance companies involved with selling annuities and pensions-related products. In order to meet future liabilities, the insurance companies and pension providers have to properly understand their longevity risk exposure.
The scenario based standard formula introduced by Solvency II imposes on calculating the Solvency Capital Requirement (SCRs) for Longevity Risk (SCRlong) according to the change in the net asset value (NAV) due to a pre-specified longevity shock. The prescribed downward shock is currently represented by a 20% permanent reduction of future mortality rates for each age and contract linked to a longevity risk. A uniform reduction of mortality rates for all ages leads to inconsistent estimates of longevity risk changing with the different considered ages [1] -[3] . In contrast to the scenario based standard formula, an internal model, which is generally stochastic and thus often more complex than the standard formula, can be taken into account the age dependence in the longevity shock highlighted by the empirical evidences [1] -[3] . As the International Association of Insurance Supervisors (IAIS) defines in the Groupe Consultasif CEA Glossary, “an internal model is a risk measurement system developed by an insurer to analyse the overall risk position, to quantify the risks and to determine the economic capital required to meet those risks” [4] .
In the present work, we explicitly model changes in the long-term longevity assumption, by suggesting an innovative approach which hinges on the stochastic volatility model and a so-called coherent risk measure as the expected shortfall. The mathematical formulation of the problem considers that being the liabilities of the life insurance company related to the longevity phenomenon volatility, the volatility evolution is described by an appropriate stochastic process.
In the traditional literature, the longevity shock is not accounted for explicitly.
We discuss about a framework based on an age-dependent longevity shock. It seems to be the only way allowing the insurer to correctly calculate the solvency capital requirement to front its future obligations.
The layout of the paper is organized as follows. In Section 2, the age-dependent internal model is introduced. Section 3 provides empirical evidence by the numerical application. In Section 4 we conclude.
2. The Age-Dependent Internal Model
In the traditional approach pension scheme actuaries implement deterministic mortality tables to calculate and value pension liabilities and to test the sensitivity of liabilities to changes in mortality rates by reasonably shifting the future mortality improvement rate up or down, or by adding one year of life expectancy to all ages in a scheme to observe the magnitude of the change.
The empirical evidence shows that stochastic mortality models provide a more accurate representation of the full distribution of possible future mortality rates [5] .
The 5th Quantitative Impact Study-QIS5 [6] , stated that the capital charge for longevity risk (from herein SCRlong) results by the net change in Net Asset Value (NAV) due to a longevity shock under a specific survival scenario at time t = 0:
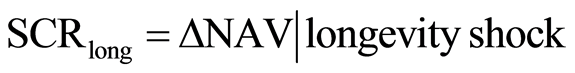 (1)
(1)
The NAV is defined by [6] as the difference between the market value of assets and liabilities. As well known, the market value of liabilities is difficult to determine, therefore it stated that it can be approximated by the so-called technical provisions which consists of the best estimate liabilities (BEL) and risk margin (RM).
The BEL is represented by “the expected or mean value (probability weighted average) of the present value of future cash flows for curren to bligations, projected over the contract’s run-off period, taking into account all up-to-date financial market and actuarial information” [4] .
The Risk Margin is calculated via a cost of capital approach and in our case considering only the longevity risk it results by the following formula:
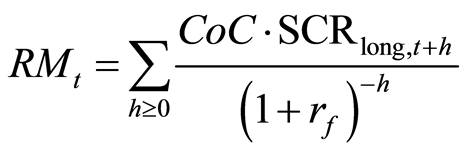 (2)
(2)
being :
CoC = the cost of capital rate;
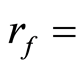 the risk free interest rate.
the risk free interest rate.
To avoid the evident situation of circularity, [6] specifies that for SCR calculation liabilities should not include Risk Margin. Therefore we have:
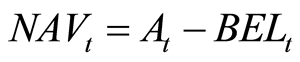 (3)
(3)
where 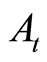 represents the market value of Assets at time t and
represents the market value of Assets at time t and 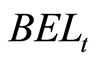 is the best estimate of liabilities at time t.
is the best estimate of liabilities at time t.
The longevity shock is fixed to be equal to a 20% mortality rates reduction for each age and contract linked to longevity risk [6] [7] . Nevertheless, a constant shock is not reasonable for all ages and maturities because of the volatility of longevity phenomenon in respect of different ages and maturities [1] .
The one-off shock structure that is equal for all ages and maturities leads to inconsistent estimation than a gradual change in mortality rates. [8] highlighted that “the shock scenario referred to by the standard formula can be far away from the actual experience of the insurer, and thus may lead to a biased allocation of capital”. In other words the standard model introduces a structural shortcoming, which contradicts the empirical evidence. This shows an age dependent shock with smaller relative reduction for old ages in respect of young ages.
In our framework, we model the longevity shock as a function of mortality rate volatility, being the time volatility 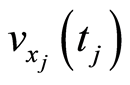 and the age volatility
and the age volatility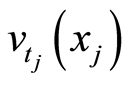 . In the former case, by fixing a single age
. In the former case, by fixing a single age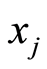 , mortality rate volatility expresses the variability of mortality as the time varies. In the latter one, by fixing a specific period
, mortality rate volatility expresses the variability of mortality as the time varies. In the latter one, by fixing a specific period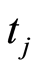 , it represents the variability of mortality as the age varies. Furthermore, in a dynamic approach of the longevity phenomenon, the shock also depends on the calendar year. On the basis of these issues, we suppose that the mortality rate volatility evolution is described by the stochastic process
, it represents the variability of mortality as the age varies. Furthermore, in a dynamic approach of the longevity phenomenon, the shock also depends on the calendar year. On the basis of these issues, we suppose that the mortality rate volatility evolution is described by the stochastic process 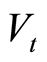 and the longevity shock
and the longevity shock  is given by:
is given by:
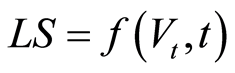 (4)
(4)
resulting as a function of the stochastic mortality rate volatility 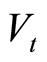 and the time
and the time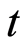 .
.
Let us suppose the PDE for longevity shock is:
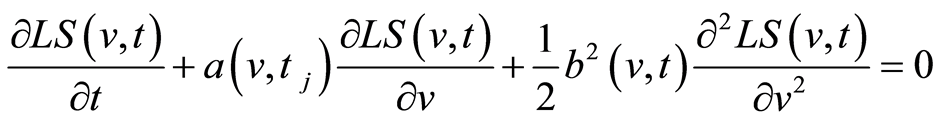 (5)
(5)
being  a solution of the deterministic PDE, under the terminal condition:
a solution of the deterministic PDE, under the terminal condition: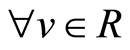
 , where
, where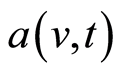 ,
,  ,
, 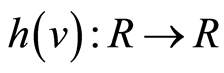 are given functions such that
are given functions such that 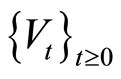 is the solution to the SDE:
is the solution to the SDE:
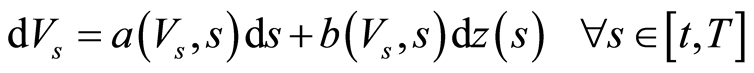 (6)
(6)
where  is a wiener process and
is a wiener process and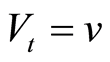 .
.
According to Feynman-Kac theorem if:
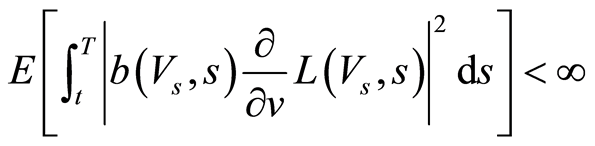
the solution to PDE has the following form:
 (7)
(7)
Formula (6) represents the stochastic evolution in time of the mortality rate volatility in the general case [9] [10] . We suppose that the mortality rate volatility is described by the square-root process as in [11] :
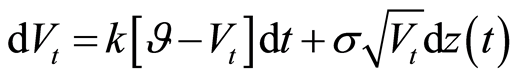
The Expected Shortfall (ES) allows to determine the expected loss incurred in the 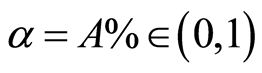 [6] [12] -[16] worst cases of our portfolio, while in the case of VaR calculation we determine the minimum loss incurred in the α worst cases of our portfolio. It is given by:
[6] [12] -[16] worst cases of our portfolio, while in the case of VaR calculation we determine the minimum loss incurred in the α worst cases of our portfolio. It is given by:
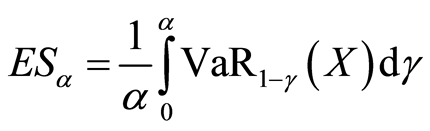 (8)
(8)
In our case X represents the loss variable defined as follows:
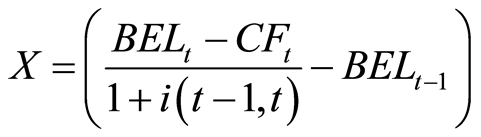 (9)
(9)
where 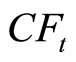 denotes the company’s stochastic cash flow at time t, it is negative in case the company pays more benefits than it receives premiums and positive otherwise.
denotes the company’s stochastic cash flow at time t, it is negative in case the company pays more benefits than it receives premiums and positive otherwise.
The SCRlong is calculated by the following approximation:
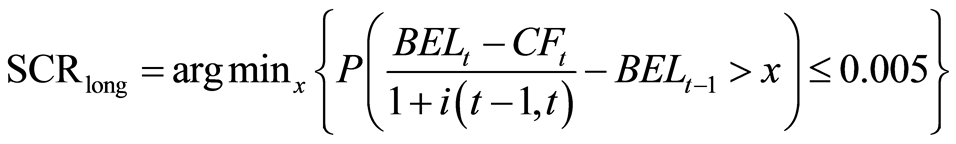 (10)
(10)
being 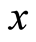 the smallest amount for which results:
the smallest amount for which results:
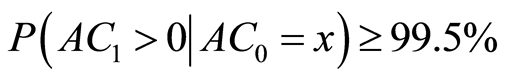
and the Available Capital at time t, 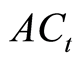 , being approximated by (3).
, being approximated by (3).
3. Numerical Applications
The numerical application considers an homogeneous portfolio of 1000 pension annuity contracts issued at age 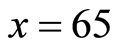 with anticipated unitary instalment payed from the retirement age 65 till the pensioner is living. The dataset is composed by the Italian male population ranging from 1950 to 2006 collected from 0 up to 110 where the survival projections are calculated according to the Poisson Lee Carter model [17] .
with anticipated unitary instalment payed from the retirement age 65 till the pensioner is living. The dataset is composed by the Italian male population ranging from 1950 to 2006 collected from 0 up to 110 where the survival projections are calculated according to the Poisson Lee Carter model [17] .
In the Table 1 we provide the calculation of the risk measures of VaR and ES on SCR according to an age-dependent longevity shock, by referring to different confidence levels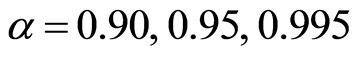 . The SCRs are calculated according to an interest rate as technical basis at level of 4.5%. The percentages at levels of 0.90 and 0.95 can meet the needs of the company, where the 0.995 is the regulatory level.
. The SCRs are calculated according to an interest rate as technical basis at level of 4.5%. The percentages at levels of 0.90 and 0.95 can meet the needs of the company, where the 0.995 is the regulatory level.
In the case of an age-dependent longevity shock, we compare the SCR obtained on the basis of different number of simulations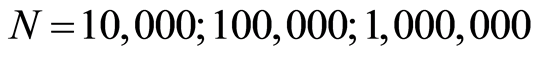 . By increasing the number of simulations, the outcomes tend to stabilize, as shown in Table 2.
. By increasing the number of simulations, the outcomes tend to stabilize, as shown in Table 2.
Table 3 computes the same aforementioned risk measures on the basis of the predefined longevity shock prescribed by Solvency II at level of 20%. By comparing the results in Table 1 with ones in Table 3, we can notice
Table 1. Age = 65, stochastic longevity shock.
Table 2. Age = 65, stochastic longevity shock, different number of simulations.
Table 3. Age = 65, 20% longevity shock.
that the allocation of capital in the case of standard formula forces the insurance company to immobilize higher resources, causing a strong bias.
4. Conclusions
Under Solvency II, insurance companies allocate capitals according to separate risk classes.
In particular, the capital charge for longevity risk results by the net change in Net Asset Value due to a constant longevity shock equal to 20%.
In this research, we propose an age-dependent internal model by representing the longevity shock on the basis of a stochastic volatility model and a coherent risk measure as the expected shortfall.
The empirical evidences show an age-dependent shock which highlights the structural shortcoming of the standard model, suggesting the inappropriateness of the regulatory configuration for calculating the solvency capital requirements.
Further researches will consider the correlation models for aggregating different forms of risk affecting insurance portfolio.
References
- Börger M. (2010) Deterministic Shock vs. Stochastic Value-At-Risk—An Analysis of the Solvency II Standard Model Approach to Longevity Risk. Blatter der DGVFM, 31, 225-259. http://dx.doi.org/10.1007/s11857-010-0125-z
- Coppola, M. and D’Amato, V. (2013) The Solvency Capital Requirement Management for an Insurance Company. ASMDA 2013 Conference, Matarò (Barcelona), 25-28 June 2013.
- Coppola, M. and D’Amato, V. (2012) Backtesting the Solvency Capital Requirement for Longevity Risk. The Journal of Risk Finance, 13, 309-319.
- IAIS (2008) International Association of Insurance Supervisors. Global Reinsurance Market Report.
- Hari, N., De Waegenaere, A., Melenberg, B. and Nijman, T.E. (2008) Longevity Risk in Portfolios of Pension Annuities. Insurance Mathematics and Economics, 42, 505-518. http://dx.doi.org/10.1016/j.insmatheco.2007.01.012
- CEIOPS (2010) QIS 5, Technical Specifications. https://eiopa.europa.eu/consultations/qis/quantitative-impact-study-5/technical-specifications/index.html
- Eiopa (2012) Technical Specifications for the Solvency II Valuation and Solvency Capital Requirements Calculations.
- Olivieri, A. and Pitacco, E. (2008) Solvency Requirements for Life Annuity: Some Comparisons. Giornale dell’Istituto Italiano degli Attuari LXXI, 1-2, 59-82.
- Schobel, R. and Zhu, J.W. (1998) Stochastic Volatility with an Ornstein-Uhlenbeck Process: An Extension. European Finance Review, 3, 46.
- Stein, J. and Stein, E. (1991) Stock Price Distributions with Stochastic Volatility: An Analytic Approach. Review of Financial Studies, 4, 727-752. http://dx.doi.org/10.1093/rfs/4.4.727
- Cox, J.C., Ingersoll, J.E. and Ross, S. (1985) A Theory of the Term Structure of Interest Rates. Econometrica, 53, 385-407. http://dx.doi.org/10.2307/1911242
- Acerbi, C. and Tasche, D. (2002) Expected Shortfall: A Natural Coherent Alternative to Value at Risk. Economic Notes, 31, 379-388. http://dx.doi.org/10.1111/1468-0300.00091
- Artzner, P., Delbaen, F., Eber, J.-M. and Heath, D. (1999) Coherent Measures of Risk. Mathematical Finance, 9, 203- 228. http://dx.doi.org/10.1111/1467-9965.00068
- CEA (2006) Working Paper on the Risk Measures VaR and TailVaR. http://ec.europa.eu/internal_market/insurance/docs/2006-markt-docs/2534-06-annex-cea_en.pdf
- Dowd, K. and Blake, D. (2006) After VaR: The Theory, Estimation, and Insurance Applications of Quantile-Based Risk Measures. Journal of Risk and Insurance, 73, 193-229. http://dx.doi.org/10.1111/j.1539-6975.2006.00171.x
- Huisman, R., Koedijk, K.G., Kool, C.J.M. and Palm, F. (2001) Tail-Index Estimates in Small Samples. Journal of Business & Economic Statistics, 19, 208-216. http://dx.doi.org/10.1198/073500101316970421
- Butt, Z. and Haberman, S. (2009) Ilc: A Collection of R Functions for Fitting a Class of Lee-Carter Mortality Models Using Iterative Fitting Algorithms. Actuarial Research Paper, No. 190.


