Applied Mathematics
Vol.4 No.9A(2013), Article ID:37406,3 pages DOI:10.4236/am.2013.49A007
Robust Pre-Attentive Attention Direction Using Chaos Theory for Video Surveillance
Department of Computer Science, Engineering and Physics, University of Michigan-Flint, Flint, USA
Email: farmerme@umflint.edu
Copyright © 2013 Michael E. Farmer. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 4, 2013; revised June 4, 2013; accepted June 11, 2013
Keywords: Image Change Detection; Image Sequence Analysis; Chaos; Fractals; Nonlinearities
ABSTRACT
Attention direction for active vision systems has been of substantial interest in the image processing and computer vision communities for video surveillance. Biological vision systems have been shown to possess a hierarchical structure where a pre-attentive processing function directs the visual attention to regions of interest which are then possibly further processed by higher-level vision functions. Biological neural systems are also highly responsive to signals which appear to be chaotic in nature. In this paper we explore applying measures from chaos theory and fractal analysis to provide a robust pre-attentive processing engine for vision. The approach is applied to two standard data sets related to video surveillance for detecting bags left suspiciously in public places. Results compare quite favorably in terms of probability of detection versus false detection rate shown through Receiver Operating Characteristic (ROC) curves against two traditional methods for low-level change detection, namely Mutual Information, Sum of Absolute Differences, and Gaussian Mixture Models.
1. Introduction
The mechanisms for directing attention in the human visual system have been the objective of significant research in the medical community and a number of computer science researchers have defined systems based on models of the human perception system [1,2]. Researchers agree that one of the “undoubtable” low level features that direct attention is motion [1]. Park et al. note “temporal saliency has high priority over spatial saliency” and Le Meur et al. note “salient parts consist of abrupt onsets” and “the appearance of new perceptual object consistent or not with the context of the scene could also attract our attention” [2]. Additionally, Wolfe notes that in the human visual system, “motion is one of the most effective pre-attentive features”, and “abrupt onset will capture attention” [3]. Likewise, “a mechanism that wanted to direct attention to any visual transient would be less useful since many uninteresting events in the world can produce such transients” [3]. One example of uninteresting transients is spatio-temporally varying illumination (i.e. moving/suddenly appearing light bands). Thus an effective pre-attentive system should detect motion and contextual change, while remaining relatively immune to spatio-temporal changes in illumination. It is important to note that pre-attentive systems are not responsible for higher level visual tasks such as segmentation, tracking, classification which occur higher in the visual processing. The proposed pre-attentive visual analysis is modeled after biological vision systems and can be very advantageous for a distributed video surveillance system where pre-attentive cues can initiate the execution of much higher complexity algorithms such as segmentation and tracking, automatic video recording, etc.
One application of computer vision that is of particular interest today is surveillance for suspicious objects left in public places, such as backpacks carrying potential explosive devices. This application is difficult since there is often considerable background motion (e.g. travelers through a train station) which can distract a vision system from detecting subtle objects of interest, and spatiotemporally varying illumination resulting both from sunlight position changes during long term visual monitoring as well as due to illumination transients due to doors opening, lighted vehicles passing through the image scene, etc. While many researchers have been exploring the issue of interesting contextual change in the presence of illumination change, these methods tend to be monolithic in structure and require considerably more processing resources than is cost-effectively available for pervasive low cost embedded applications [4-8].
While there are very few actual pre-attentive processing systems proposed, there are many change detection and background subtraction algorithms in the literature that provide the users usually segmentations of the change or identification of image frames within which change occurred. This is particularly popular in areas of remote sensing and surveillance. Remote sensing applications typically employ some form of pixel-level subtraction [9- 11]; which will then result in these “approaches suffering from differences in image radiometry” [10]. Change detection for video surveillance is commonly based on background subtraction and one common method for performing this task is eigen-backgrounds [12], which manage the background information through the principle components of the image greyscale amplitudes, and update the background based on pixel amplitude changes relative to the model. Clearly any of these systems that employ pre-attentive algorithms are based on simple image differencing will not be immune to illumination changes and many of the authors directly acknowledge this [2, 8,10]. Another common method around for surveillance systems is Gaussian Mixture Models (GMM) [8]. As with the other common methods, however GMMs are not robust to illumination changes [8]. Additionally, methods such as eigen-backgrounds and GMM require considerably additional processing to perform contextual change detection (long-term scene change) [8,12].
The author’s recent work in modeling moving objects in image fields as aperiodic forcing functions impacting the imaging sensor and thereby creating chaos-like signals in phase space has been shown to be robust to detecting change and motion while ignoring illumination effects. The underlying processing of the proposed method is based on fractal analysis of the image amplitude phase plot and requires relatively simple processing that would be suitable for high speed pre-attentive processing required for distributed video surveillance systems.
In this paper we initially review the fact that contextual change in images results in chaos-like fractal behavior in phase space, while change due to illumination is topologically compact and non-fractal. We then discuss a suitable fractal measure for performing chaos theory inspired analysis of image sequences to quantify these different behaviors of illumination and change. We will then provide a processing framework for pre-attentive vision for video surveillance using the proposed chaos-based approach. Lastly, we demonstrate its performance against the problem of suspicious left bags in complex real-world scenes, including a crowded subway station.
2. Characteristics of Image Change
The two mechanisms through which the pixel amplitudes of a perceived image can change are: (i) due to illumination and (ii) due to appearance changes of objects within the image. These appearance changes can be caused by one of two mechanisms (i) change in position due to motion, and (ii) sudden appearance due to an object being left in a scene. In [13-15] the author has shown that these changes can be modeled effectively by considering objects moving through an image scene as aperiodic forcing functions which impact the imaging sensor and produce chaos-like behavior in the pixel amplitudes. This paper provides an extended coverage of the applications of chaos specifically to attention direction initially provided in [15]. Velazquez used the aperiodic forcing function model to explain the signals behavior of biological neural systems [16]. A useful tool for analyzing chaos-like behavior in dynamical systems is the phase plot of the system over time. Previously, the author has demonstrated that the phase plots exhibit the principle of ergodicity which allows analysis of the temporal behavior of a single particle (in our case a pixel) to be replaced with analyzing an ensemble of particles at a single time instance (an image pair in our application) [13,14]. This is a significant benefit as it greatly reduces the time frames within which events can be detected. This is critical for a preattentive system since requiring temporal analysis of long trajectories would add significant latencies into the analysis, while frame-wise analysis supports real-time lowlatency processing. The critical distinctions between the effects of illumination and the effects of contextual change will be addressed in the following two sub-sections.
2.1. Image Illumination Change
The effects of illumination on images within video sequences have been shown by the author [13] and in parallel by Cho et al. to result in a multiplicative change 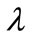 in illumination in the Lambertian scene radiance,
in illumination in the Lambertian scene radiance,  , described by [17]:
, described by [17]:
 , (1)
, (1)
where 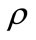 is the albedo of the object surface,
is the albedo of the object surface, 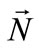 is the normal to the surface of the object, and
is the normal to the surface of the object, and 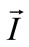 is the directional illumination. Mester, et al. has also noted the multiplicative nature of illumination and they developed a co-linearity model where changes in illumination are assumed constant over small regions. Then by treating local neighborhoods of pixels as a vector they define the illumination change as a scaling operation of one vector relative to another [6]. Likewise for specular objects the scene a more complex reflectance models, such as the Torrance-Sparrow model which combines specular and diffuse components of scene radiance, can be used [18]:
is the directional illumination. Mester, et al. has also noted the multiplicative nature of illumination and they developed a co-linearity model where changes in illumination are assumed constant over small regions. Then by treating local neighborhoods of pixels as a vector they define the illumination change as a scaling operation of one vector relative to another [6]. Likewise for specular objects the scene a more complex reflectance models, such as the Torrance-Sparrow model which combines specular and diffuse components of scene radiance, can be used [18]:
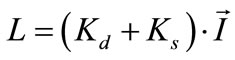 (2)
(2)
where 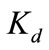 is the diffuse component, and
is the diffuse component, and 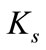 is the speculative component of the surface. This more complex model still maintains the basic form of the illumination multiplied by a surface descriptor, which implies illumination changes can be modeled multiplicatively by:
is the speculative component of the surface. This more complex model still maintains the basic form of the illumination multiplied by a surface descriptor, which implies illumination changes can be modeled multiplicatively by:
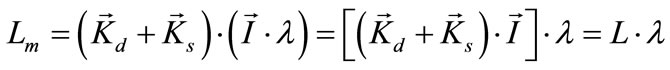 (3)
(3)
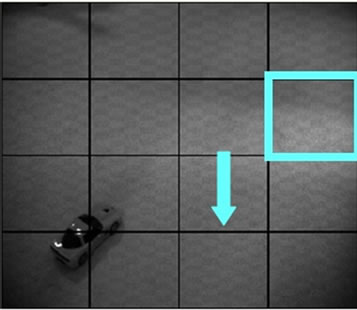
The effects in phase space between an image pair experiencing spatio-temporally varying illumination changes are provided in Figure 1 where the reader is directed to note the locally compact conical structure in the phase plot due to spatio-temporal variation in the illumination. Also note the verification of the multiplicative illumination model where the higher amplitude pixels (further up on the phase plot) are shifted by a greater amount. Figure 2 provides an even more telling demonstration of the power of analyzing images in phase space rather than in traditional grayscale space. In Figures 2(a) and (b) we see the original background image and an image from a sequence with a subway entering a station. Note the strong angle of the phase plot in Figure 2(c) due to the significant increase in global illumination due to the car. Likewise note the conical structure of the phase plot in Figure 2(d) due to the spatial variation of illumination due to the windows of the car. Section 3 of this paper will highlight the algorithm used to allow us to ignore these illumination changes.
Black, et al. attempt to model all possible conditions of change, including illumination, motion, deformation, noise, etc. [5], and use mixture modeling to identify pixels corresponding to each of these possible change mechanisms. The use of mixture models is further extended in Tian, et al where multiple Gaussian mixtures (GMMbased methods) are used to model all possible illumination changes without assumptions of them being due to moving objects, contextual change, illumination or shadows [8]. The limitations of the approach are “it cannot
 (a)
(a)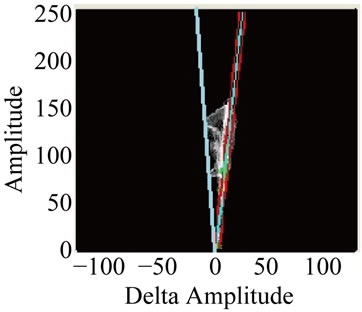 (b)
(b)
Figure 1. Effects of spatio-temporally varying illumination: (a) image with spatially varying illumination change (vector shows direction of motion of illumination in subsequent frames), (b) phase plot showing conic structure due to multiplicative nature of illumination.
 (a)
(a) (b)
(b) (c)
(c)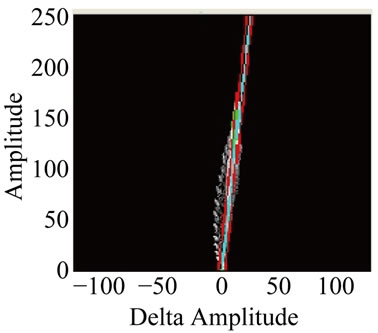 (d)
(d)
Figure 2. Effects of spatio-temporally varying illumination and demonstration of its multiplicative nature: (a) background image; (b) future image with subway present and significant complex spatially varying illumination change from windows, headlights, etc.; (c) phase plot showing effect in phase space of global illumination change in region (4, 4), and (d) conic structure of phase plot due to spatially varying illumination in region (2, 4).
adapt to quick-lighting changes and cannot handle shadows well” [8].
The issue of rapidly changing illumination failing for GMM approaches is also particularly problematic for a pre-attentive vision system since it would cause high numbers of false alarms. This can be seen clearly in Figure 3 through Figure 4 where two subsequences of the subway data are processed using GMM. Figure 3(a) shows the subway entering the station and Figure 4(a) shows the GMM detections for that and a subsequent image only four time samples apart. Likewise Figure 3(b) and Figure 4(b) show the illumination effects detected by GMM for a later segment of the image sequence. Note the significant illumination detections in Figure 4 when these images are only separated by a short time interval, when compared to the huge time variation between the two images in Figure 2 for the phase plot generations. The next section will reinforce that when analyzing images in phase space there is a clear distinction between changes due to illumination and changes due to contextual change that cannot be captured by traditional grayscale methods such as SAD [19] and GMM [8].
In addition to reducing the false alarm rate of detecting actual contextual change due to illumination changes this powerful feature of phase space analysis has a profound effect on background image generation and management.
 (a)
(a) (b)
(b)
Figure 3. Typical image with interesting spatio-temporally varying illumination: (a) moving subway car, and (b) subway car doors open and shadows from people exiting.
 (a)
(a) (b)
(b)
Figure 4. Detected changes due to illumination that is ignored by chaos theory but detected GMM using filtered data: (a) for image in Figure 3(a) where illumination is detected by GMM in grid cell (2,1) and (2,2) and (b) for image sequence in Figure 3(b) where extensive illumination is detected by GMM in grid cells (1,3), (2,3), (3,1), and (4,1).
One of the key reasons GMM is quite popular is that it adjusts the background over time as illumination changes. Of course it needs to do this otherwise the GMM algorithm will detect illumination change as real change. Unfortunately, rapidly changing illumination cannot be integrated effectively into the background model and likewise cannot be removed from the background once it is integrated due to the slow time constraints of the mixture model evolution. The proposed chaos-based approach does not require an updated background image when there is illumination change, as the change can be detected by its unique behavior in phase space relative to substantive contextual change. The background images in this study were actually pieced together from sections of multiple images across all of the I-Lids dataset, with the regions selected solely on their lack of objects, irrespective of the overall illumination. This provides a significant advantage for the proposed chaos-based approach over all traditional methods.
2.2. Image Change Due to Motion or Context
Recall that changes in an image that are of interest are due to object motion or object appearance. We can see from Equation (2) that the changes in reflectance occurring in the scene within a region captured by a pixel due to either motion of an object or the sudden appearance of an object result in non-linear multiplicative effects through the dot product of the surface normal (and its related albedo) with the illumination source. Cho and Kim in [17] witnessed non-linearities in the joint histograms but treated them as outliers that confounded their computation of a global illumination change rather than analyzing them as a source of contextual change in images. The framewise phase plot interestingly is also structurally similar to the joint histogram of Cho and Kim [17]. Le Meur, et al. recognized and used nonlinear models to describe the stimulation of visual cells in biological systems [2]. Additionally, Nagao, et al. explained the rapid transition of human recognition between two objects in the visual system through the transition between competing basins of attraction in a chaotic system [20].
Figure 5(c) shows the phase space trajectory due to motion between image pairs (Figure 5(a) and Figure 5(b)) exhibits interesting chaos-like behavior when viewed in the phase space of pixel amplitudes. Likewise Figure 5(f) shows the phase space trajectory due to contextual change resulting from a left bag (Figure 5(e) versus Figure 5(d)). Notice these trajectories are considerably more complex than those shown in Figures 2(c) and (d). Tel and Gruiz also state, “[one difference] between chaotic and non-chaotic systems is that, in the former case, the phase space objects… trace out complicated (fractal) sets, whereas in the non-chaotic case the objects suffer weak deformations” [21]. Clearly there is a distinct difference in the behavior of the phase plots from illumination change as from motion and contextual change, which we will exploit in this approach.
Our proposed chaos-based approach directly exploits the underlying differing mechanisms of contextual change versus illumination change to devise a method for detecting the meaningful contextual change irrespective of the existing illumination and any illumination changes. An effective pre-attentive vision system should not precompensate or attempt to characterize illumination changes as in [6] or [19], but rather it should attempt to directly isolate regions of interest with contextually interesting change while being less sensitized to simple illumination change. As shown in Figure 5 the non-linear effects of the modeling change as aperiodic forcing functions results in complex behavior in phase space, and we will show that this complex behavior can be effectively quantified through fractal measures, and these measures can serve as a robust indicator of the presence of change in an image sequence for identifying regions of interest in pre-attentive processing.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d) (e)
(e) (f)
(f)
Figure 5. Chaotic behavior due to motion and contextual change: (a) first image with motion; (b) second image with motion; (c) phase plot; (d) first image with contextual change; (e) second image with contextual change, and (f) phase plot.
3. Pre-Attentive Processing Using Fractal Analysis in Phase Space
The processing flow for the proposed system is provided in Figure 6. The initial step of low-pass filtering reduces the effects of noise and can also support down-sampling for even higher performance. Note that both the chaos measures and the traditional Mutual Information and sum of absolute differences (SAD) are global dimensions. For attention direction, however, we are interested in more than simply knowing an entire image has motion or contextual change, but rather a coarse focusing of attention

Figure 6. Chaos-based pre-attentive processing.
to the sub-region in the image where the change occurs, to allow us to more efficiently direct our more complex computational resources associated with the higher level vision processing. Consequently, rather than applying this measure to the entire image, the image is divided into a 4 × 4 grid of sub-image cells and the measures are computed within these smaller regions. Future work is directed at integrating a quad-tree approach where regions are further subdivided based on possible characteristics of the resultant phase plots. Bang, et al. apply a SAD measure at a block level as well to provide regional detection for that method as well [19].
There are then two nearly identical parallel paths for this processing, one for motion and one for contextual change. The only difference between the two paths is that in the motion processing there is a determination of time lag to be used between images while in the context path; the reference image is always used as the first image in the comparison. For selecting time lags, the system currently uses one to eight image frame time lags for motion depending on the type of scene and objects (human versus automobile for example), and uses a reference image constructed earlier to serve as the contextual change reference image.
The next processing task is Compute Phase Plots where each pixel in one image is paired with the same pixel location in the second image. The amplitude of the pixel determines the y-axis location in phase space and the difference between the two pixels determines the xaxis location. For each pair of pixels, the corresponding (amplitude, delta-amplitude) phase plot location is incremented by one.
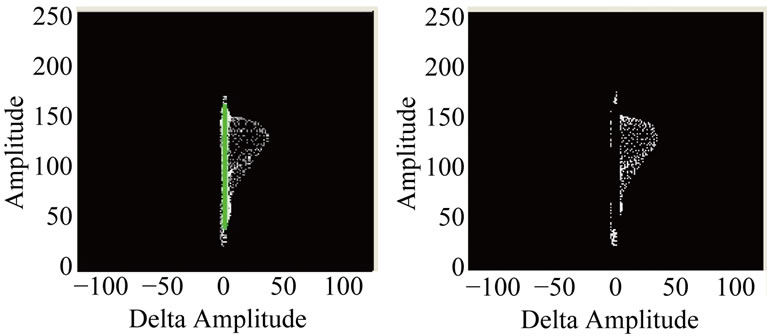
The Detect and Remove Background task uses the phenomena that the background is straight forward to detect in phase space; even if there have been illumination changes as was shown in Section 2-A. In phase space the background appears as a straight line, with the slope of the line being determined by the change in global illumination between the two image frames. Illumination with spatial variation appears as a cone in phase space as shown earlier in Figure 1(b). The processing flow for Detect and Remove Background is provided in Figure 7. The first step in the processing is the threshold the phase plot to remove the lower amplitude trajectories which corresponds to any motion and spatially varying illumination, and leaves the background with any global illumination. The background always results in higher amplitudes in the phase plot, even with global illumination change since there is no complex trajectory which spreads the amplitude throughout the phase space. This is a unique advantage of analyzing the signals in phase space, since background is always higher amplitude than complex illumination or motion trajectories. The threshold is initially set at 10% of the phase plot peak, and if the number of detected points is too low the threshold is reduced and the phase plot re-tested until at least ten points are detected to construct the line fit for the removal of any globally illuminated background from the phase plot.
The background removal estimates the width and slope of the dominant line in the phase plot with the base of the line occurring at zero amplitude and zero amplitude change as shown in Figure 8. Note we use the transpose of the phase plot so we do not need to deal with infinite slopes. The power of using the mathematical structure of illumination change is provided by the fact that both SAD [19] and GMM methods [8] treat all grayscale differences the same while our proposed chaos-based approach takes advantage of the structural differences in phase space between illumination change and motion/ contextual change, thereby allowing it to effectively ignore illumination change in subsequent processing. GMM methods, such as those defined in [8], rely on extensive post-processing to remove regions with illumina-

Figure 7. Chaos-based background removal processing.
 (a) (b)
(a) (b)
Figure 8. Rotated phase plots with line fit and width of background to remove: (a) phase plot for grid cell (2, 2) in Figures 3(a) and (b) phase plot for grid cell (3, 1) in Figure 3(b).
tion change, using computationally demanding methods such as texture comparison, and they remain highly sensitive to fast illumination changes. The benefits of the proposed approach over grayscale methods such as GMM can be seen when the reader contrasts with the minimal change in phase space in Figures 8(a) and (b) due to illumination change with the resultant GMM-processed images in Figure 3.
Figure 9 shows the results of the background removal process where after the line and width are computed (highlighted in Figure 9(a)), the background in phase space is masked and the resultant phase plot (Figure 9(b)) is then ready to compute the fractal dimension. There are three classes of measures from the domain of fractal analysis can be used for computing fractal dimensions in the Compute Fractal Dimension task: (i) morphological dimensions, (ii) entropy dimensions and (iii) transform dimensions [22]. We will be employing the morphological dimension in this work.
Most morphological-based dimension measures are either directly related to or motivated by the Hausdorff dimension, 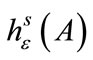 which is defined as [23]:
which is defined as [23]:
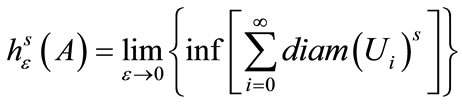 , (4)
, (4)
where 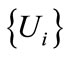 is the set of hyperspheres of dimension s and of diameter of
is the set of hyperspheres of dimension s and of diameter of , providing an open cover over space A.
, providing an open cover over space A.
While the Hausdorff dimension is a member of the morphological dimensions, it is not easily calculated. Fortunately, there are numerous dimensions, such as the Box Counting dimension which are closely related (and provably upper bounds to the Hausdorff dimension) and is attractive because it is relatively easy to compute. The Box Counting dimension,  , is defined as [23]:
, is defined as [23]:
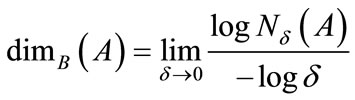 , (5)
, (5)
where  is the smallest number of boxes of size
is the smallest number of boxes of size 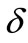 that cover the space A. Very simply, the Box Count-
that cover the space A. Very simply, the Box Count-
 (a) (b)
(a) (b)
Figure 9. Removal of background contribution to phase plot prior to computation of the fractal dimension, (a) phase plot with background line highlighted, and (b) phase plot with background portion of phase plot removed.
ing dimension is a computation of the number of boxes of a given size within which some portion of the trajectory can be found. Note, however, that it does not count how many points from the trajectory fall within the box.
Another closely related dimension is the Information dimension which is also quite popular and in some cases believed to be more effective, but slightly more complicated to compute compared to the Box Counting method [24]. The Information dimension provides a weight as to how often the trajectory can be found in the box and is defined based on Shannon’s definition of the sum of the information across all boxes at a given resolution [25]:
 (6)
(6)
The Information dimension is then defined to be [25]:
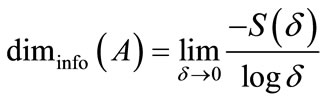 (7)
(7)
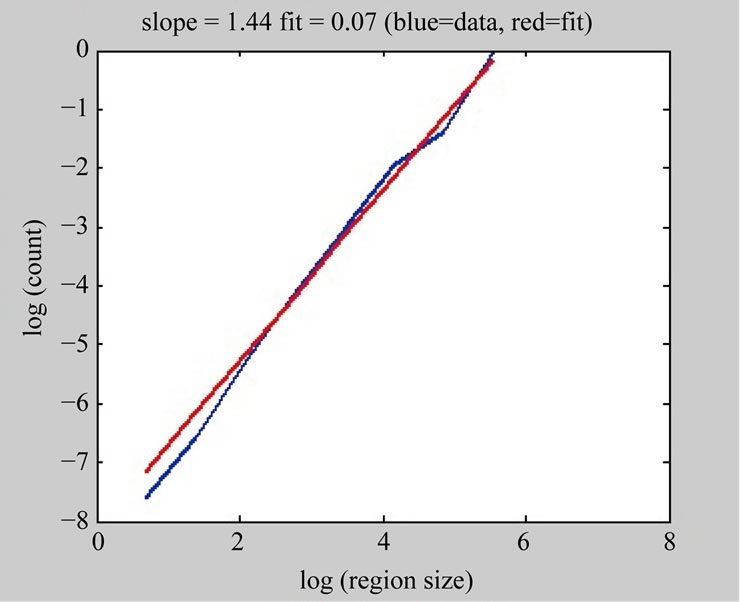
The management of the box sizes and their overlay upon the phase plot are identical in each method and Figure 10 shows excerpts from the sequence of boxes of increasingly finer resolution and their resulting cover of the phase plot. For each method, a simple least squares fit of the log-log plot of the number of boxes required for the cover versus the size of the boxes used provides the final dimensional measure. Figure 11(a) shows the resultant least squares line fit that is used to compute the actual Box Counting dimension. Note that at both extremes of the calculation, the data deviates from a straight line. This is a well-known effect, and it is recommended that the end points corresponding to one box the size of the image and to boxes the size of an individual pixel be ignored [23]. The resultant dimensional measure computed using either the Box Counting or Information dimension methods will allow us to quickly detect possible non-linear dynamics in the phase plot to identify regions of an image sequence where interesting (i.e. not illuminationbased) change has been detected.
Other approaches for pre-attentive change include the sum of absolute differences (SAD), Mutual Information, and GMM [2,5,8,11,19,26,27]. SAD is simply computed by computing the difference between two images and computing the absolute value of each difference, while Mutual Information involves the calculation of [26]:
 (a)
(a) (b)
(b) (c)
(c)
Figure 10. Calculation of box counting for phase plot showing recursively smaller boxes overlaid on regions containing trajectory.
 (a)
(a)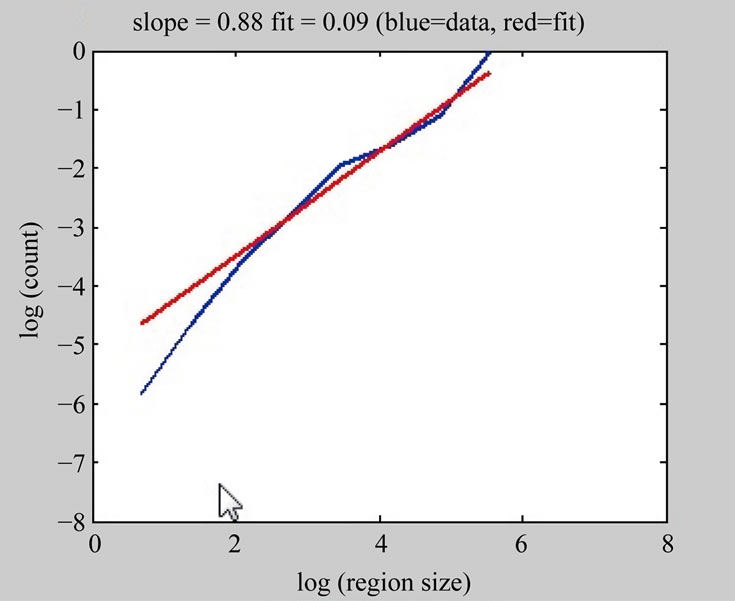 (b)
(b)
Figure 11. Calculation of box counting for (a) box counting calculation shown in Figure 10, and (b) box counting calculation for illumination-only phase plot in Figure 2(b).
 (8)
(8)
where  and
and  are the individual distributions of data sets A and B, and
are the individual distributions of data sets A and B, and  is the joint distribution of data sets A and B, and a is a value in dataset A and b is a value in dataset B. Note that image differencing and mixture models are not immune to illumination which can dramatically change the SAD value. Likewise Mutual Information can be insensitive to small changes in an image since it is overwhelmed by the constant background contribution and it can also be affected by illumination change since it results in changes in the joint histogram used to calculate the MI. GMM relies on calculating images of the number of mixtures, mean, variance, and weight of every pixel in the image for each of the collection of mixtures which results in considerable processing [8].
is the joint distribution of data sets A and B, and a is a value in dataset A and b is a value in dataset B. Note that image differencing and mixture models are not immune to illumination which can dramatically change the SAD value. Likewise Mutual Information can be insensitive to small changes in an image since it is overwhelmed by the constant background contribution and it can also be affected by illumination change since it results in changes in the joint histogram used to calculate the MI. GMM relies on calculating images of the number of mixtures, mean, variance, and weight of every pixel in the image for each of the collection of mixtures which results in considerable processing [8].
The final step of processing is Select Grid Cell of Interest which passes the detected regions of interest on to the higher level attentive processing. There are two complementary goals of this step, either process regions of interest to detect long term change or process them to detect motion to match the objective of the system being developed. The objective of the proposed system is to detect regions with long term change related to detecting left bags. The proposed system sets two flags for each grid cell if there are detections in the motion or the context processing, respectively. Only the grid cells with long term contextual change detected but no short term motion detected will be passed on to the attentive processing engine.
4. Results
A collection of interesting left-bag scenarios from the CAVIAR and AVSS-2007 datasets [28,29] are used to demonstrate the benefits of the proposed chaos-based approach using Box Counting or the Information dimension and the traditional approaches, SAD, MI, and GMM. The CAVIAR data sets are interesting because the bags are left near large objects which would make it very difficult for human observers to readily detect the objects. The AVSS images are interesting because of the significant distracting motion and spatio-temporal illumination present in the sequences due to both the subway cars that transit the station and the crowds of people they discharge. Two image sequences are used from each of the collections. All of these sequences were hand-processed off-line to develop ground truth files to identify regions where there was one of four possibilities: (i) nothing, (ii) motion, (iii) non-bag contextual change (e.g. subway car), and (iv) a left bag. The left bag that must be detected in the CAVIAR 1 data set is shown in Figure 12(b), left bag that must be detected in the CAVIAR 2 data set is shown in Figure 12(a), the left bag in the AVSS Easy dataset is shown in Figure 12(d), and the left bag in the AVSS Medium dataset is shown in Figure 12(c).
We provide results in terms of Receiver Operating Characteristics (ROC) curves Figure 13 through Figure 20. The results provided in these comprehensive sets of data clearly demonstrate the performance improvement of the chaos-based methods over the traditional methods for all four data sets and for detecting motion as well as contextual change from left bags. We provide ROC curves for motion detection with the time-lag between frames being set to four frames (Figure 13 through Figure 16). The actual selection of the time lag is based on the expected speed of motion within the image sequences; hence for human detection the time lag would be larger than for vehicle detection. This is an intuitive parameter to set based on the application domain. While it was not
 (a)
(a) (b)
(b) (c)
(c) (d)
(d) (e)
(e) (f)
(f) (g)
(g) (h)
(h)
Figure 12. Fractal measure versus object of interest size:, (a) grayscale region showing bag from CAVIAR-2; (b) phase plot of region with fractal measure 1.21; (c) grayscale region showing bag from, CAVIAR-1; (d) phase plot of region with fractal measure 1.37; (e) grayscale region showing bag from AVSS_medium; (f) phase plot of region with fractal measure 1.42; (g), grayscale region showing bag, from AVSS-Easy and (h) phase plot of region with fractal measure 1.62.
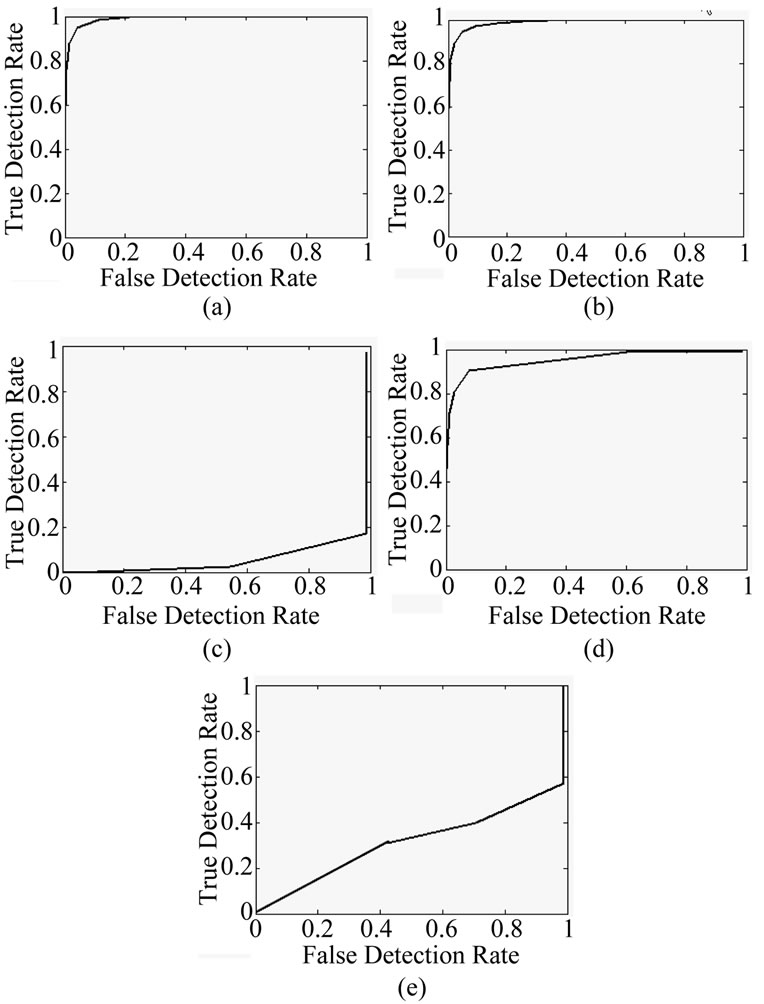
Figure 13. Motion (delta t = 4 frames) ROC curves for AVSS easy, (a) Box counting; (b) Information dimension; (c) Mutual Information; (d) SAD; and (e) GMM.
part of this study, it is possible to automatically scroll through a range of time-lags where the maximum delay is defined by the application.
In all the ROC curves the chaotic approaches worked better both for motion and for contextual detection. In the

Figure 14. Motion (delta t = 4 frames) ROC curves for AVSS medium, (a) Box counting; (b) Information dimension; (c) Mutual information; (d) SAD; and (e) GMM.

Figure 15. Motion (delta t = 4 frames) ROC curves for CAVIAR I, (a) Box counting; (b) Information dimension; (c) Mutual information; (d) SAD; and (e) GMM.

Figure 16. Motion (delta t = 4 frames) ROC curves for CAVIAR II, (a) Box counting; (b) Information dimension; (c) Mutual information; (d) SAD; and (e) GMM.

Figure 17. Contextual change detection ROC curves for AVSS easy, (a) Box counting; (b) Information dimension; (c) Mutual information; and (d) SAD.
comparison between chaos and MI, the results are indeed compelling. Likewise the comparison of the chaos-based methods to GMM is also dramatic. GMM suffered lower performance compared to the chaos-base methods due to illumination sensitivity and ghosting due to the slow recovery from objects moving through the grid cells. For the comparison between chaos and SAD, the chaos
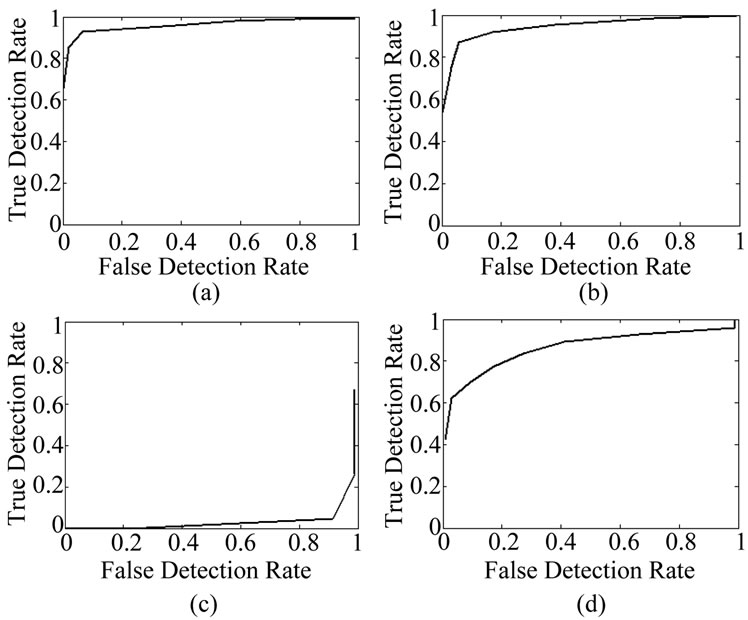
Figure 18. Contextual change detection ROC curves for AVSS medium, (a) Box counting; (b) Information dimension; (c) Mutual information; and (d) SAD.

Figure 19. Contextual change detection ROC curves for CAVIAR I, (a) Box counting; (b) Information dimension; (c) Mutual information; and (d) SAD.
methods performed better in every image sequence. Interestingly, the simpler Box Counting method performed slightly better than the Information dimension.
Two example sets of grid cells detected contextual change from the AVSS sequences are provided in Figures 21(a) and (b). Note that in Figure 21(b) the subway car is present in the left of the image and a person is detected standing at the ticket machine in the upper right grid cell of the image. In Figure 21(a) a number of people are standing quite still or sitting on the benches waiting for a subway car. For these cases, the higher level vision system would sort out the longer term tracking of these objects and similar to the tracking algorithms employed by Tian [8]. Therefore many of the detections of all three approaches are legitimate change that pre-atten-

Figure 20. Contextual change detection ROC curves for CAVIAR II, (a) Box counting; (b) Information dimension, (c) Mutual information; and (d) SAD.
 (a)
(a) (b)
(b)
Figure 21. Examples of regions where no immediate motion is detected but there is significant contextual change, (a) people being relatively still, and (b) subway car stopped at station on left side and person at ATM.
tion would detect but not be responsible for resolving.
One significant advantage of the chaos approaches is the intuition which can be applied in setting the thresholds as they are set directly on the amount of information change the operator is interested in seeing. The MI and SAD approaches, however, rely on adaptive thresholding based on image amplitude information which can be very difficult to set as can be seen in the three plots in Figure 22. The threshold values for SAD which varied by a factor of 5 and was extremely difficult to set due to no clear modality in the histogram as can be seen in Figure 22(c). Likewise setting the threshold automatically for the MIbased detector was impossible due to the complexity of the histogram of values as can be seen in Figure 22(b).
GMM relies on thresholding at the desired percent of detected pixels in the image grid cell, which is often quite large due to the fact that the moving person dropping a bag is much larger than the bag being discarded. Additionally, there is a variety of parameters that must be set for GMM as well, namely the initial variance, the learning rate, the number of mixtures, the fraction of region with change, and the decay rate for the Zivkovic method
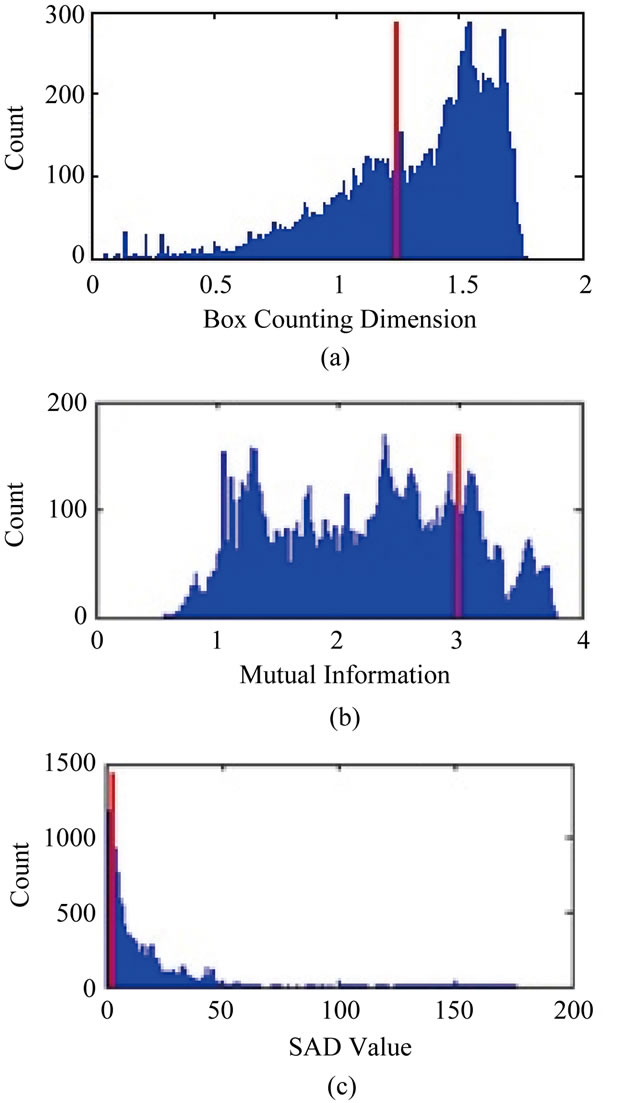
Figure 22. Histograms of measures for motion and contextual change for the AVSS sequence in Figure 24, (a) chaos measure for motion; (b) chaos measure for context; (c) MI measure for motion; (d) MI measure for context; (e) SAD measure for motion; and (f) SAD measure for context.
[27]. Note that all of these are based on the expected grayscale behavior in the image rather than on any intrinsic characteristics of the objects being detected. These grayscale behaviors are extremely difficult to anticipate and are highly variable across applications.
The limitations of all the other methods are in sharp contrast to the detection threshold and time lags for the chaos-based approach. In the chaos approach the threshold is based on how fractal the phase plot should appear for the desired change detection sensitivity. The fractal value of the phase plot is directly related to the space filling nature of the phase space trajectory which is a measure of the amount of information created in the image sequence. Thus the fractality is directly related to the desired object size to be expected by the desired contextual change. Likewise the time lag is directly related to the anticipated motion characteristics of the object which are commonly known for the desired application.
Figures 23(a)-(c) and Figures 24(a)-(c) show baseline images and a typical frame pair from a sequence of realtime images from CAVIAR and AVSS indoor surveil-
 (a)
(a) (b)
(b) (c)
(c) (d)
(d) (e)
(e) (f)
(f) (g)
(g)
Figure 23. Results of attention direction to contextual change, (a) original empty image; (b) image at time one; (c) image at time two; (d) motion-based phase space; (e) contextual change phase space; (f) phase space showing (context-motion) regions; and (g) resultant regions in image.
lance datasets. In each figure, subplot (d) is the motionbased phase plots, and subplot (e) is the long-term contextual phase plot. Subplot (f) in each of these is the region remaining after using the motion windows to ignore regions in the contextual plot where the change in scene has been determined to be motion, and subplot (g) in each case shows the resultant grayscale image. Notice that in both cases the bags which were left are detected. In Figure 24(g) there is also a significant region of spatio-temporal illumination change in the lower left that still passed detection. This region has a slightly elevated fractal dimension since the illumination change is due to complex moving illumination patterns caused by passengers in the subway door. Most other spatial-temporal illumination regions in the image have been successfully ignored by the chaos-based methods, as can be seen by the lower false alarm rate inferred from the ROC curves.
In summary, the benefits of using the chaos-based approach are: (i) it is amplitude independent, unlike a simple difference measure such as Sum of Absolute Differences (SAD) which often requires adaptive thresholding [17], (ii) it allows the user to define a threshold based
 (a)
(a) (b)
(b) (c)
(c) (d)
(d) (e)
(e) (f)
(f) (g)
(g)
Figure 24. Another result of attention direction due to contextual change, (a) original empty image; (b) image at time one; (c) image at time two; (d) motion-based phase space; (e) contextual change phase space; (f) phase space showing (context-motion) regions; and (g) resultant regions in image.
on the relative change in information in the image based on the characteristics of the objects of interest rather than the grayscale behavior, and (iii) it is less sensitive to illumination change, being invariant to global changes and typically having a lower value for a broad spectrum of spatio-temporal illumination changes.
5. Conclusions and Future Work
In this paper we presented an approach to pre-attentive processing based not only on the structural form of biological vision systems, but also on the characteristics of the neural waveforms. The approach is based on a model of object changes serving as aperiodic forcing functions which drive non-linear behavior in the imaging sensor resulting in complex trajectories in pixel amplitude phase space. The fractality of the phase space trajectories is a direct measure of the information content within the trajectory, thereby serving as a direct measure of pre-attentive interest unlike other common measures such as image amplitude difference or mutual information which measure directly in grayscale space. The approach also exploits the fact that effects due to illumination changes are non-chaotic and follow highly deterministic and hence dense and non-fractal trajectories in phase space, thereby making the approach less sensitive than the other approaches, particularly SAD and GMM, to spatio-temporally varying illumination.
The approach is demonstrated on two standard data sets and shows that the chaos-based approaches provide a robust and efficient algorithm for developing a pre-attentive vision processing system. Future work will be focused in three directions, (i) determining additional measures to work with the fractal dimension for detecting the unique nature of spatio-temporal illumination in phase space, (ii) developing an interaction between the contextual and motion processing for determining optimal time lags for each grid cell and (iii) continuing the application of chaotic measures to higher level vision at the attentive and post-attentive processing stages. The work directed at (i) will investigate additional detectors of phase space structure beyond the fractal dimension to handle the most complex spatio-temporally varying illumination, since as stated by Tricot in [30], “The measure of a set does not determine its topological properties”. Thus it should be possible to consider additional topological measures to differentiate these changes from contextual change. The addition of any algorithmic sophistication must be weighted carefully against the added processing burden since pre-attentive processing must be simple and high speed.
REFERENCES
- J. M. Wolfe and T. S. Horowitz, “What Attributes Guide the Deployment of Visual Attention and How Do They Do It?” Neuroscience, Vol. 5, 2004, pp. 1-7.
- O. LeMeur, P. LeCallet, D. Barba and D, Thoreau, “A Coherent Computational Approach to Model Bottom-Up Visual Attention,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 28, No. 5, 2006, pp. 802-817. doi:10.1109/TPAMI.2006.86
- J. M. Wolfe, “Visual Attention,” In: K. K. DeValois, Ed., Seeing, 2nd Edition, Academic Press, Amsterdam, 2000, pp. 335-386. doi:10.1016/B978-012443760-9/50010-6
- R. J. Radke, S. Andra, O. Al-Kofahi and B. Roysam, “Image Change Detection Algorithms: A Systematic Survey,” IEEE Transactions on Image Processing, Vol. 14, No. 3, 2005, pp. 294-307. doi:10.1109/TIP.2004.838698
- M. J. Black, D. J. Fleet and Y. Yacoob, “Robustly Estimating Changes in Image Appearance,” Computer Vision and Image Understanding, Vol. 78, 2000, pp. 8-31. doi:10.1006/cviu.1999.0825
- R. Mester, T. Aach and L. Dumbgen, “Illumination-Invariant Change Detection Using a Statistical Colinearity Criterion,” Proceedings of the 23rd Symposium DAGM on Pattern Recognition, 2001, pp. 170-177.
- M. C. Park, K. J. Cheoi and T. Hamamoto, “A Smart Image Sensor with Attention Module,” Proceedings of the 7th IEEE Workshop on Computer Architecture for Machine Perception, 2005, pp 46-51. doi:10.1109/CAMP.2005.7
- Y. Tian, R. S. Feris, H. Liu, A. Hamparar and M.-T. Sun, “Robust Detection of Abandoned and Removed Objects in Complex Surveillance Videos,” IEEE Transactions on Systems, Man, and Cybernetics-Part C: Applications and Reviews, future issue, 2010.
- F. Wang, Y. Wu, Q. Zhang, P. Zhang, M. Li and Y. Lu, “Unsupervised Change Detection on SAR Images Using Triplet Markov Field Model,” IEEE Geoscience and Remote Sensing Letters, Vol. 10, No. 4, 2013, pp. 697-701. doi:10.1109/LGRS.2012.2219494
- L. Bruzzone and F. Bovolo, “A Novel Framework for the Design of Change-Detection Systems for Very-High-Resolution Remote Sensing Images,” Proceedings of the IEEE, Vol. 101, No. 3, 2013, pp. 609-630. doi:10.1109/JPROC.2012.2197169
- Y. Pu, W. Wang and Q. Xu, “Image Change Detection Based on the Minimum Mean Square Error,” Proceedings of IEEE 5th International Joint Conference on Computational Sciences and Optimization, 2012, pp. 367-371.
- Y. Tian, Y. Wang, Z. Hu and T. Huang, “Selective Eigen Background for Background Modeling and Subtraction in Crowded Scenes,” IEEE Transactions on Circuits and Systems for Video Technology, preprint, 2013.
- M. Farmer, “A Chaos Theoretic Analysis of Motion and Illumination in Video Sequences,” Journal of Multimedia, Vol. 2, No. 2, 2007, pp. 53-64. doi:10.4304/jmm.2.2.53-64
- M. Farmer and C. Yuan, “An Algorithm for Motion and Change Detection in Image Sequences Based on Chaos and Information Theory,” Proceedings of the SPIE, Vol. 6812, 2008, pp. 68120K-68120K-12. doi:10.1117/12.766934
- M. E. Farmer, “A Comparison of a Chaos-Theoretic Method for Pre-Attentive Vision with Traditional GrayscaleBased Methods,” Proceedings of the IEEE Conference on Advanced Video and Signal-Based Surveillance, 2011, pp. 337-342.
- J. L. P. Velaquez, “Brain, Behaviour, and Mathematics: Are We Using the Right Approaches?” Physica D, No. 212, 2005, pp. 161-182. doi:10.1016/j.physd.2005.10.005
- J.-H. Cho and S.-D. Kim, “Object Detection Using MultiResolution Mosaic in Image Sequences,” Signal Processing: Image Communication, Vol. 20, 2005, pp. 233-253. doi:10.1016/j.image.2004.12.001
- I. Sato, Y. Sato and K. Ikeuchi, “Illumination from Shadows,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 25, No. 3, 2003, pp. 290-300. doi:10.1109/TPAMI.2003.1182093
- J. Bang, D. Kim and H. Eom, “Motion Object and Regional Detection Method Using Block-based Background Difference Video Frames,” Proceedings of the IEEE International Conference on Embedded and Real-Time Computing Systems and Applications, 2012, pp. 350-357.
- N. Nagao, H. Nishimura and N. Matsui, “A Neural Chaos Model of Multistable Perception,” Neural Processing Letters, Vol. 12, No. 3, 2000, pp. 267-276. doi:10.1023/A:1026511124944
- T. Tel and M. Gruiz, “Chaotic Dynamics,” Cambridge, 2006.
- W. Kinsner, “A Unified Approach to Fractal Dimensions,” Proceedings of the IEEE Conference on Cognitive Informatics, 2005, pp. 58-72.
- H. O. Peitgen, H. Jurgens and D. Saupe, “Chaos and Fractals,” Springer, Berlin, 1992. doi:10.1007/978-1-4757-4740-9
- A. J. Roberts, “Use the Information Dimension, Not the Hausdorff,” Nonlinear Sciences, 2005, pp. 1-9.
- J. Theiler, “Estimating Fractal Dimension,” Journal Optical Society of America, Vol. 7, No. 6, 1990, pp. 1055- 1073. doi:10.1364/JOSAA.7.001055
- D. Russakoff, C. Tomasi, T. Rohlfing and C. R. Maurer, “Image Similarity Using Mutual Information of Regions,” Proceedings of the 8th European Conf. on Computer Vision, 2004, pp. 596-607.
- Z. Zivkovic and F. van der Heijden, “Efficient Adaptive Density Estimation per Image Pixel for the Task of Background Subtraction,” Pattern Recognition Letters, Vol. 27, No. 7, 2006, pp. 773-780. doi:10.1016/j.patrec.2005.11.005
- CAVIAR Project/IST 2001 37540. http://homepages.inf.ed.ac.uk/rbf/CAVIAR/
- I-Lids Dataset for AVSS 2007.
- C. Tricot, “Curves and Fractal Dimension,” SpringerVerlag, Berlin, 1995. doi:10.1007/978-1-4612-4170-6

