Applied Mathematics
Vol.4 No.3(2013), Article ID:28852,5 pages DOI:10.4236/am.2013.43069
Derivative of a Determinant with Respect to an Eigenvalue in the LDU Decomposition of a Non-Symmetric Matrix
Department of Architecture, School of Industrial Engineering, Tokai University, Toroku, Kumamoto, Japan
Email: mkashi@ktmail.tokai-u.jp
Received October 11, 2012; revised November 11, 2012; accepted November 18, 2012
Keywords: Derivative of Determinant; Non-Symmetric Matrix; Eigenvalue; Band Matrix; LDU Decomposition
ABSTRACT
We demonstrate that, when computing the LDU decomposition (a typical example of a direct solution method), it is possible to obtain the derivative of a determinant with respect to an eigenvalue of a non-symmetric matrix. Our proposed method augments an LDU decomposition program with an additional routine to obtain a program for easily evaluating the derivative of a determinant with respect to an eigenvalue. The proposed method follows simply from the process of solving simultaneous linear equations and is particularly effective for band matrices, for which memory requirements are significantly reduced compared to those for dense matrices. We discuss the theory underlying our proposed method and present detailed algorithms for implementing it.
1. Introduction
In previous work, the author used the trace theorem and the inverse matrix formula for the coefficient matrix appearing in the conjugate gradient method to propose a method for derivative a determinant in an eigenvalue problem with respect to an eigenvalue [1]. In particular, we applied this method to eigenvalue analysis and demonstrated its effectiveness in that setting [2-4]. However, the technique proposed in those studies was intended for use with iterative methods such as the conjugate gradient method and was not applicable to direct solution methods such as the lower-diagonal-upper (LDU) decomposition, a typical example. Here, we discuss the derivative of a determinant with respect to eigenvalues for problems involving LDU decomposition, taking as a reference the equations associated with the conjugate gradient method [1]. Moreover, in the Newton-Raphson method, the solution depends on the derivative of a determinant, so the result of our proposed computational algorithm may be used to determine the step size in that method. Indeed, the step size may be set automatically, allowing a reduction in the number of basic parameters, which has a significant impact on nonlinear analysis. For both dense matrices and band matrices, which require significantly less memory than dense matrices, our method performs calculations using only the matrix elements within a certain band of the matrix factors arising from the LDU decomposition. This ensures that calculations on dense matrices proceed just as if they were band matrices. Indeedcomputations on dense matrices using our method are expected to require only slightly more computation time than computations on band matrices performed without our proposed method. In what follows, we discuss the theory of our proposed method and present detailed algorithms for implementing it.
2. Derivative of a Determinant with Respect to an Eigenvalue Using the LDU Decomposition
The eigenvalue problem may be expressed as follows. If  is a non-symmetric matrix of dimension
is a non-symmetric matrix of dimension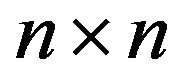 , then the usual eigenvalue problem is
, then the usual eigenvalue problem is
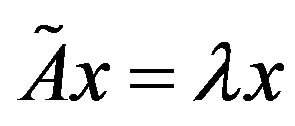 , (1)
, (1)
where  and
and 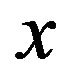 denote respectively an eigenvalue and an corresponding eigenvector. In order for Equation (1) to have nontrivial solutions, the matrix
denote respectively an eigenvalue and an corresponding eigenvector. In order for Equation (1) to have nontrivial solutions, the matrix 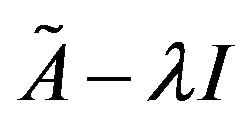 must be singular, i.e.,
must be singular, i.e.,
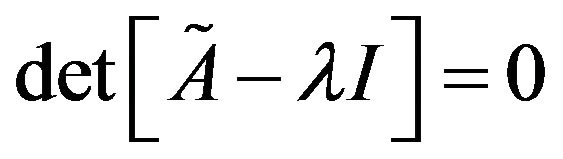 . (2)
. (2)
We introduce the notation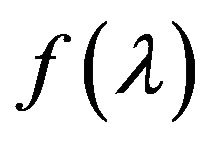 for the left-hand side of this equation:
for the left-hand side of this equation:
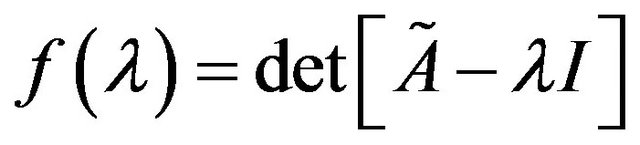 . (3)
. (3)
Applying the trace theorem, we obtain
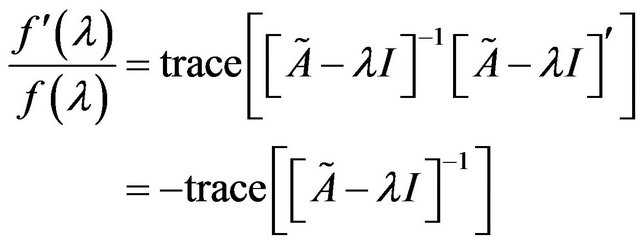 , (4)
, (4)
where
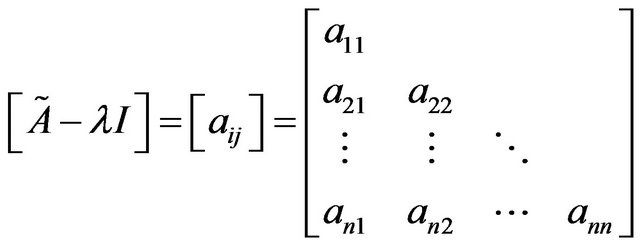 . (5)
. (5)
The LDU decomposition decomposes this matrix into a product of three factors:
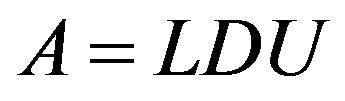 , (6)
, (6)
where the L, D, and U factors have the forms
 , (7)
, (7)
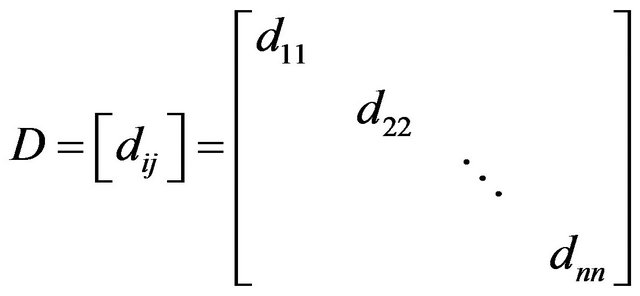 , (8)
, (8)
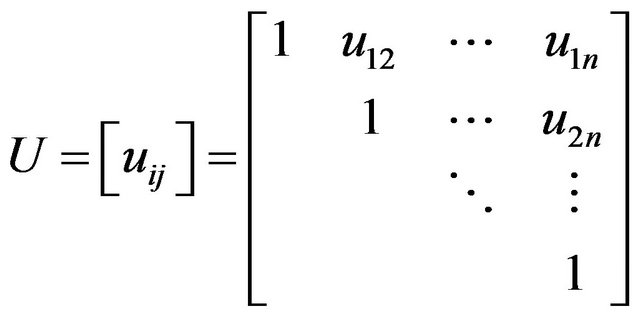 . (9)
. (9)
We write the inverse of the L factor in the form
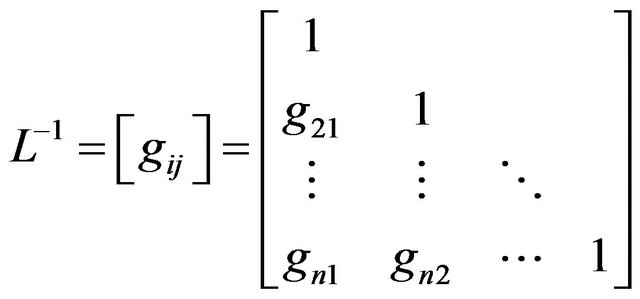 . (10)
. (10)
Expanding the relation 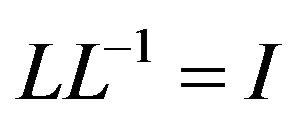 (where I is the identity matrix), we obtain the following expressions for the elements of
(where I is the identity matrix), we obtain the following expressions for the elements of :
:
 ,
,
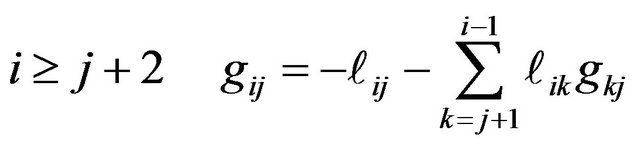 . (11)
. (11)
Next, we write the inverse of the U factor in the form
 . (12)
. (12)
Expanding the relation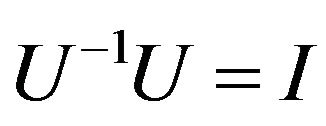 , we again obtain expressions for the elements of
, we again obtain expressions for the elements of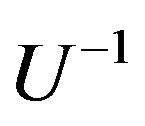 :
:
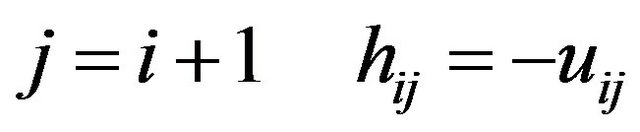 ,
,
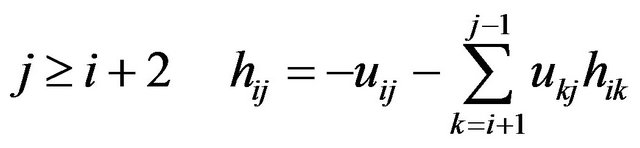 . (13)
. (13)
Equations (11) and (13) indicate that 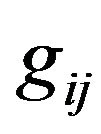 and
and 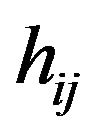 must be computed for all matrix elements. However, for matrix elements outside the half-band, we have
must be computed for all matrix elements. However, for matrix elements outside the half-band, we have 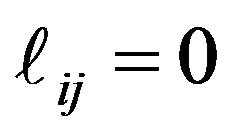 and
and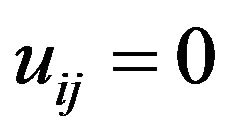 , and thus the computation requires only elements
, and thus the computation requires only elements 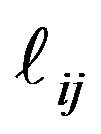 and
and  within the half-band. Moreover, the narrower the half-band, the more the computation time is reduced.
within the half-band. Moreover, the narrower the half-band, the more the computation time is reduced.
From Equation (4), we see that evaluating the derivative of a determinant requires only the diagonal elements of the inverse of the matrix A in (6). Using Equations (7)- (10), and (12) to evaluate and sum the diagonal elements of the product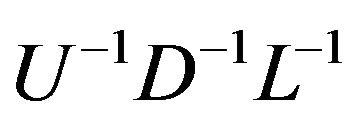 , we obtain the following representation of Equation (4):
, we obtain the following representation of Equation (4):
 . (14)
. (14)
This equation demonstrates that the derivative of a determinant may be computed from the elements of the inverses of the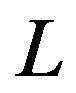 ,
,  , and
, and  matrices obtained from the LDU decomposition of the original matrix. As noted above, the calculation uses only the elements of the matrices within a certain band near the diagonal, so computations on dense matrices may be handled just as if they were band matrices. Thus we expect an insignificant increase in computation time as compared to that required for band matrices without our proposed method.
matrices obtained from the LDU decomposition of the original matrix. As noted above, the calculation uses only the elements of the matrices within a certain band near the diagonal, so computations on dense matrices may be handled just as if they were band matrices. Thus we expect an insignificant increase in computation time as compared to that required for band matrices without our proposed method.
By augmenting an LDU decomposition program with an additional routine (which simply appends two vectors), we easily obtain a program for evaluating . Such computations are useful for numerical analysis using algorithms such as the Newton-Raphson method or the Durand-Kerner method. Moreover, the proposed method follows easily from the process of solving simultaneous linear equations.
. Such computations are useful for numerical analysis using algorithms such as the Newton-Raphson method or the Durand-Kerner method. Moreover, the proposed method follows easily from the process of solving simultaneous linear equations.
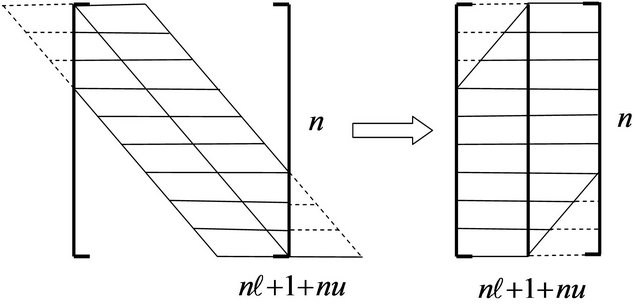
3. Algorithms for Implementing the Proposed Method
3.1. Algorithm for Dense Matrices
We first discuss an algorithm for dense matrices. The arrays and variables are as follows.
1) LDU decomposition and calculation of the derivative of a determinant with respect to an eigenvalue
(1) Input data A: given coefficient matrix2-dimensional array of the form A(n,n)
b: work vector, 1-dimensional array of the form b(n)
c: work vector, 1-dimensional array of the form c(n)
n: given order of matrix A and vector b eps: parameter to check singularity of the matrix
(2) Output data A: L matrix, D matrix and U matrix2-dimensional array of the form A(n,n)
fd: derivative of determinant
ierr; error code
=0, for normal execution
=1, for singularity
(3) LDU decomposition do i=1,n
do k=1,i-1
A(i,i)=A(i,i)-A(i,j)*A(j,j)*A(j,i)
end do
if (abs(A(i,i)) ierr=1 return end if do j=i+1,n do k=1,i-1 A(j,i)=A(j,i)-A(j,k)*A(k,k)*A(k,i) A(i,j)=A(i,j)-A(i,k)*A(k,k)*A(k,j) end do A(j,i)=A(j,i)/A(i,i) A(i,j)=A(i,j)/A(i,i) end do end do ierr=0 (4) Derivative of a determinant with respect to an eigenvalue fd=0 <(i,i)>. do i=1,n fd=fd-1/A(i,i) end do <(i,j)> do i=1,n-1 do j=i+1,n b(j)=-A(j,i) c(j)=-A(i,j) do k=1,j-i-1 b(j)=b(j)-A(j,i+k)*b(i+k) c(j)=c(j)-A(i+k,j)*c(i+k) end do fd=fd-b(j)*c(j)/A(j,j) end do end do 2) Calculation of the solution (1) Input data A: L matrix, D matrix and U matrix 2-dimensional array of the form A(n,n) b: given right-hand side vector 1-dimensional array of the form b(n) n: given order of matrix A and vector b (2) Output data b: work and solution vector, 1-dimensional array (3) Forward substitution do i=1,n do j=i+1,n b(j)=b(j)-A(j,i)*b(i) end do end do (4) Backward substitution do i=1,n b(i)=b(i)/A(i,i) end do do i=1,n ii=n-i+1 do j=1,ii-1 b(j)=b(j)-A(j,ii)*b(ii) end do end do 3.2. Algorithm for Band Matrices We next discuss an algorithm for band matrices. Figure 1 depicts a schematic representation of a band matrix. Here 1) LDU decomposition and calculation of the derivative of a determinant with respect to an eigenvalue (1) Input data A: given coefficient band matrix2-dimensional array of the form A(n,nl+1+nu) b: work vector, 1-dimensional array of the form b(n) c: work vector, 1-dimensional array of the form c(n) n: given order of matrix A nl: given left half-band width of matrix A nu: given right half-band width of matrix A eps: parameter to check singularity of the matrix (2) Output data A: L matrix, D matrix and U matrix2-dimensional array of the form A(n,nl+1+nu) fd: derivative of determinant ierr: error code =0, for normal execution =1, for singularity (3) LDU decomposition do i=1,n Figure 1. Band matrix. do j=max(1,i-min(nl,nu)),i-1 A(i,nl+1)=A(i,nl+1) -A(i,nl+1-(i-j))*A(j,nl+1)*A(j,nl+1+(i-j)) end do if (abs(A(i,nl+1)) ierr=1 return end if do j=i+1,min(i+nl,n) sl=A(j,nl+1-(j-i)) do k=max(1,j-nl),i-1 sl=slA(j,nl+1-(j-k))*A(k,nl+1)*A(k,nl+1+(i-k)) end do A(j,nl+1-(j-i))=sl/A(i,nl+1) end do do j=i+1,min(i+nu,n) su=A(i,nl+1+(j-i)) do k=max(1,j-nu),i-1 su=su-A(i,nl+1-(i-k))*A(k,nl+1)*A(k,nl+1+(j-k)) end do A(i,nl+1+(j-i))=su/A(i,nl+1) end do end do ierr=0 (4) Derivative of a determinant with respect to an eigenvalue fd=0 <(i,i)> do i=1,n fd=fd-1/A(i,nq) end do <(i,j)> do i=1,n-1 do j=i+1,min(i+nl,n) b(j)=-a(j,nl+1-(j-i)) do k=1,j-i-1 b(j)=b(j)-a(j,nl+1-(j-i)+k)*b(i+k) end do end do do j=i+nl+1,n b(j)=0.d0 do k=1,nl b(j)=b(j)-a(j,k)*b(j-nl-1+k) end do end do do j=i+1,min(i+nu,n) c(j)=-a(i,nl+1+(j-i)) do k=1,j-i-1 c(j)=c(j)-a(i+k,nl+1+(j-i)-k)*c(i+k) end do end do do j=i+nu+1,n c(j)=0.d0 do k=1,nu c(j)=c(j)-a(i,nl+1+k)*c(j-nl-1+k) end do end do do j=i+1,n fd=fd-b(j)*c(j)/a(j,nl+1) end do 2) Calculation of the solution (1) Input data A: given decomposed coefficient band matrix2-dimensional array of the form A(n,nl+1+nu) b: given right-hand side vector 1-dimensional array of the form b(n) n: given order of matrix A and vector b nl: given left half-band width of matrix A nu: given right half-band width of matrix A (2) Output data b: solution vector, 1-dimensional array (3) Forward substitution do i=1,n do j=max(1,i-nl),i-1 b(i)=b(i)-A(i,n+1-(i-j))*b(j) end do end do (4) Backward substitution do i=1,n ii=n-i+1 b(ii)=b(ii)/a(ii,nl+1) do j=ii+1,min(n,ii+nu) b(ii)=b(ii)-a(ii,nl+1+(j-ii))*b(j) end do end do 4. Conclusion We have demonstrated that, when computing the LDU decomposition (a typical example of a direct solution method), it is possible simultaneously to obtain the derivative of a determinant with respect to an eigenvalue. In addition, in the Newton-Raphson method, the solution depends on the derivative of a determinant, so the result of our proposed computational algorithm may be used to determine the step size in that method. Indeed, the step size may be set automatically, allowing a reduction in the number of basic parameters, which has a significant impact on nonlinear analysis. Our proposed method is based on the LDU decomposition, and for band matrices the memory required to store the LDU factors is significantly reduced compared to the case of dense matrices. By augmenting an LDU decomposition program with an additional routine (which simply appends two vectors), we easily obtain a program for evaluating the derivative of a determinant with respect to an eigenvalue. The result of this computation is useful for numerical analysis using such algorithms as those of the Newton-Raphson method and the Durand-Kerner method. Moreover, the proposed method follows easily from the process of solving simultaneous linear equations and should prove an effective technique for eigenvalue problems and nonlinear problems. REFERENCES denotes the left half-bandwidth, and
denotes the left half-bandwidth, and 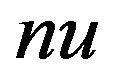 denotes the right half-bandwidth. These numbers do not include the diagonal element, so the total bandwidth is
denotes the right half-bandwidth. These numbers do not include the diagonal element, so the total bandwidth is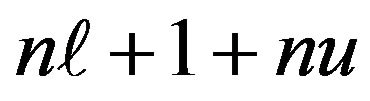 .
.