Applied Mathematics
Vol.4 No.10(2013), Article ID:37481,7 pages DOI:10.4236/am.2013.410190
Variational Iteration Method Solutions for Certain Thirteenth Order Ordinary Differential Equations
1Department of Mathematics, Yaba College of Technology, Lagos, Nigeria
2Department of Mathematics, University of Lagos, Lagos, Nigeria
3Department of Mechanical Engineering, Yaba College of Technology, Lagos, Nigeria
Email: adebaba2001@yahoo.com
Copyright © 2013 Tunde A. Adeosun et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 2, 2013; reivsed May 2, 2013; accepted May 9, 2013
Keywords: Variational Iteration Method; Boundary Value Problems; Linear and Nonlinear Problems; Approximate Solution
ABSTRACT
In this paper, we extend variational iteration method (VIM) to find approximate solutions of linear and nonlinear thirteenth order differential equations in boundary value problems. The method is based on boundary valued problems. Two numerical examples are presented for the numerical illustration of the method and their results are compared with those considered by [1,2]. The results reveal that VIM is very effective and highly promising in comparison with other numerical methods.
1. Introduction
Boundary Value Problems (BVPs) in linear and nonlinear differential equations has been one of the major problems. Many phenomena in applied Mathematics and other sciences can be described very successfully by models using mathematical tools from ordinary differential equations. [3-5] claimed that ODE has gained much attention recently due to exact description of nonlinear phenomena. In the past, both Mathematicians and Physicists have made significant progress in this direction. Analytical methods that are commonly used to solve nonlinear equations are very restricted and numerical methods involving description of variables on the other hand give rise to rounding off errors. Since these equations are linear and nonlinear, it may not have precise analytical solutions. On the other hand, solving these differential equations analytically may guide Mathematicians to know how to describe some physical process deeply and sometimes lead to know some facts which are not simply understood through common observations. As a result, these equations have to be solved using other methods.
References [6,7] gave examples on the free vibration analysis of beam structure that is governed by a fourthorder differential equation and ring structured by a sixthorder differential equation. Moreover, when considering the instability setting in an infinite horizontal layer of fluid, which is heated from below and is subject to the action of rotation, we may model the instability as ordinary convention and over stability by a sixth-order Ordinary Differential Equation (ODE) and an eighth-order ODE respectively. Even higher order ODE can be involved when a uniform magnetic field is applied across the fluid in the same direction as gravity. Ordinary convention and over stability yield a tenth order and a twelfth order ODEs respectively. Such problems modeled by high-order differential equations are often associated with initial boundary conditions, so that the problem is well posed. References [8,9] provided examples on the beam vibration problem, which is governed by a fourth-order differential equation, has four boundary conditions. It is noted that for well-posed problems, the number of boundary conditions is the same as the order of the differential equation and in general they are only given at each boundary [10-12].
In this present work, Variational Iteration Techniques for the solution of thirteen order boundary value problem is studied, following the variational iteration techniques for the solution of eight order boundary value problems.
2. Variational Iteration Analysis
To illustrate the basic concept of the variational iteration method, we consider the following general system.
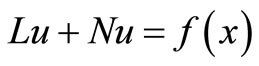 (1)
(1)
where ![]() is a linear operator,
is a linear operator, 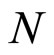 a nonlinear operator and
a nonlinear operator and 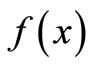 is a forcing term. Following the variational iteration technique used in [13-17], a correct functional can be constructed as
is a forcing term. Following the variational iteration technique used in [13-17], a correct functional can be constructed as
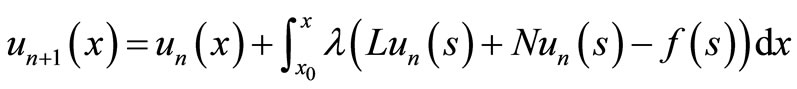 (2)
(2)
where ![]() is a Lagrange multiplier, which can be identified optimally via variational iteration method. It may be mentioned that
is a Lagrange multiplier, which can be identified optimally via variational iteration method. It may be mentioned that ![]() denotes the
denotes the 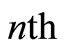 approximation
approximation  is considered to be restricted variation i.e.
is considered to be restricted variation i.e.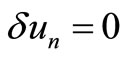 . It may also be noted that the Equation (2) is known as a correct functional.
. It may also be noted that the Equation (2) is known as a correct functional.
Due to the exert identification of the Lagrange multiplier, the solution of the linear problems can be determined in a single iteration step. The following system of differential equations helps in understanding the variational iteration method.
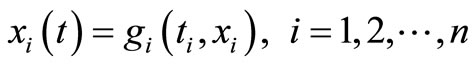 (3)
(3)
along in the boundary conditions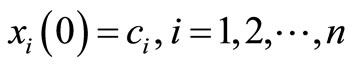 .
.
The system (3) is rewritten as
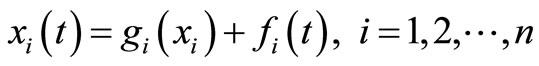
The following system is used to approximate the correct functional for the nonlinear system. (see (4) below)
where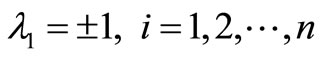 are Lagrange multipliers, while
are Lagrange multipliers, while  denote the restricted variations.
denote the restricted variations.
The following iterative scheme can be obtained for
 as (see (5) below)
as (see (5) below)
Considering the initial guess values to be 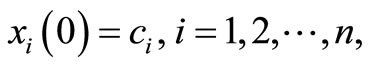
The final approximation solution can be written as  can be terminated after suitable number of iterations.
can be terminated after suitable number of iterations.
3. Mathematical Formulation
The basic motivation of this research work is to apply the variational iteration technique to solve a system of differential equations. The boundary value problem, to be solved is as follows
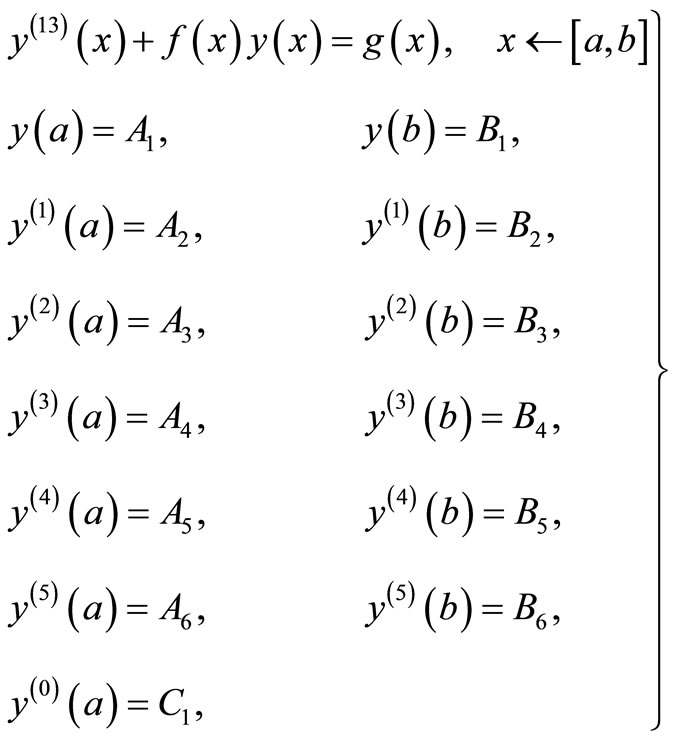 (6)
(6)
where 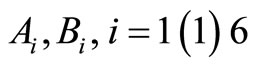 and
and ![]() are the finite real constants and functions
are the finite real constants and functions 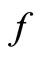 is continuous on
is continuous on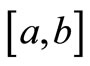 .
.
4. Numerical Examples
To implement the method developed, two examples are considered.
Example 1
For 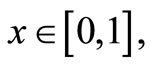 the following linear boundary value problem is considered
the following linear boundary value problem is considered
 (4)
(4)
 (5)
(5)
 (7)
(7)
The analytical solution of the given problem from [8]
 (8)
(8)
The given thirteen order BVP can be transferred with the following system
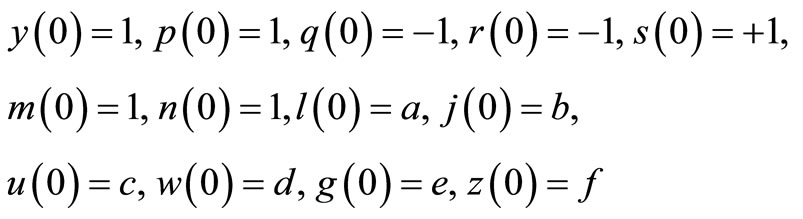
This system of differential equation can be written in terms of the following system of integral equation with Lagrange multipliers 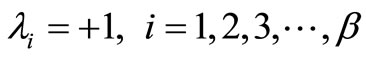
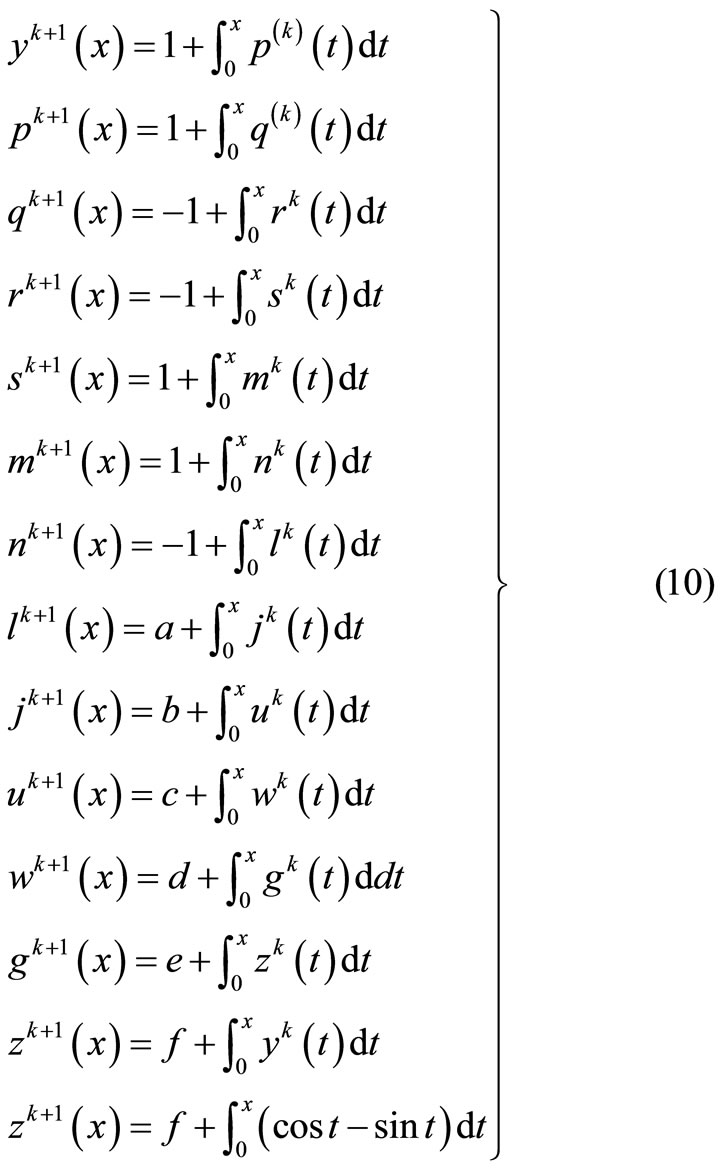
where
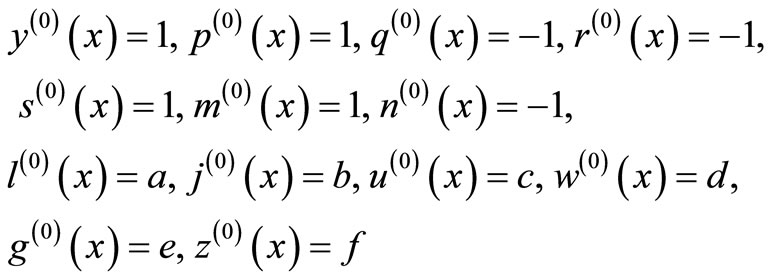
The system of Equation (11) will provides the following approximations
When 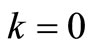
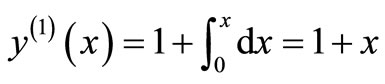

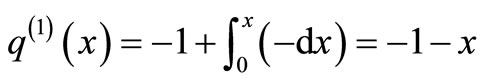



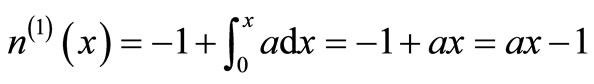

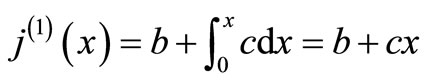



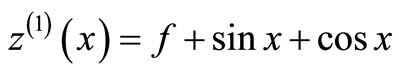

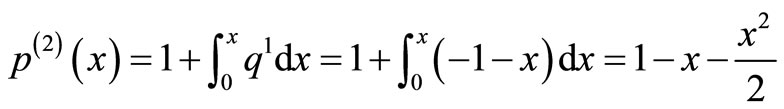
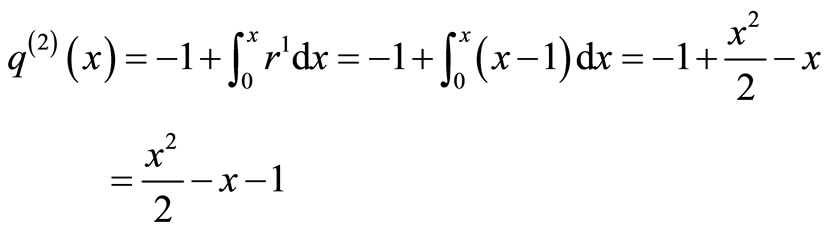
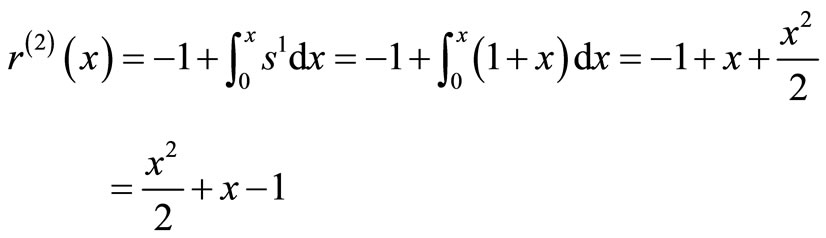

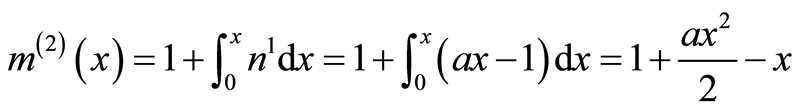

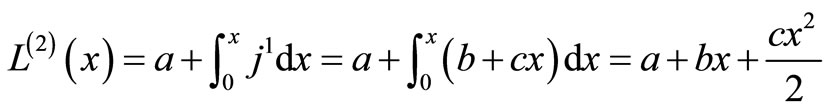
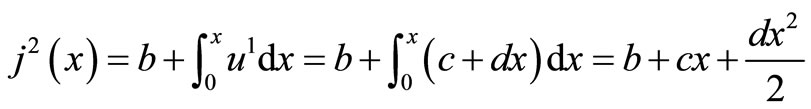
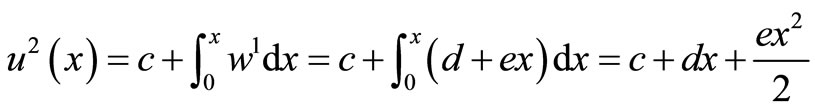





The solution is given as
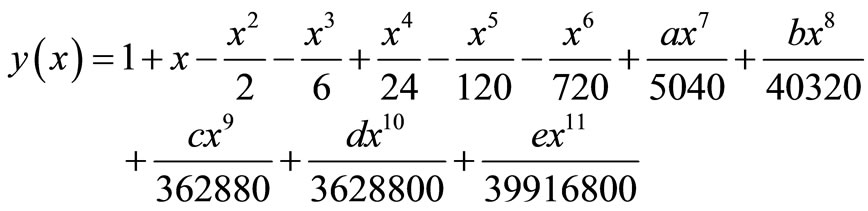 (11)
(11)
The coefficients 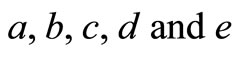 are obtained using MAPLE 13 with boundary condition at
are obtained using MAPLE 13 with boundary condition at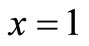 , which gives
, which gives

The series solution can thus, be written as
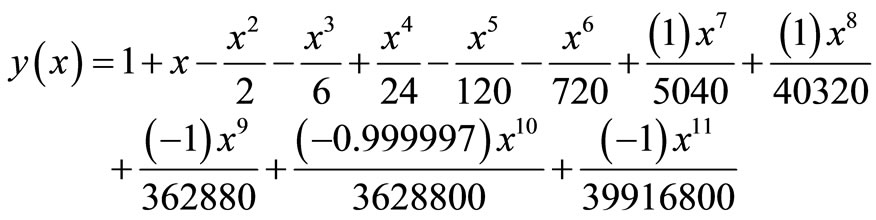 (12)
(12)
Example 2
For  the following linear boundary value problem is considered
the following linear boundary value problem is considered
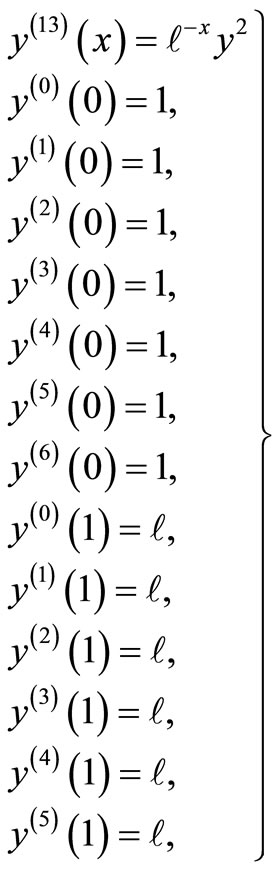 (13)
(13)
The analytical solution of the given problem from [18]
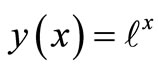 (14)
(14)
The given thirteen order boundary value problem can be transformed with the following system

with

This system of differential Equations (14) can be written in terms of the following system of integral equations with Lagrange multipliers 
 (16)
(16)
with
 (17)
(17)
The above system of differential Equations (16) and (17) provide the following approximations
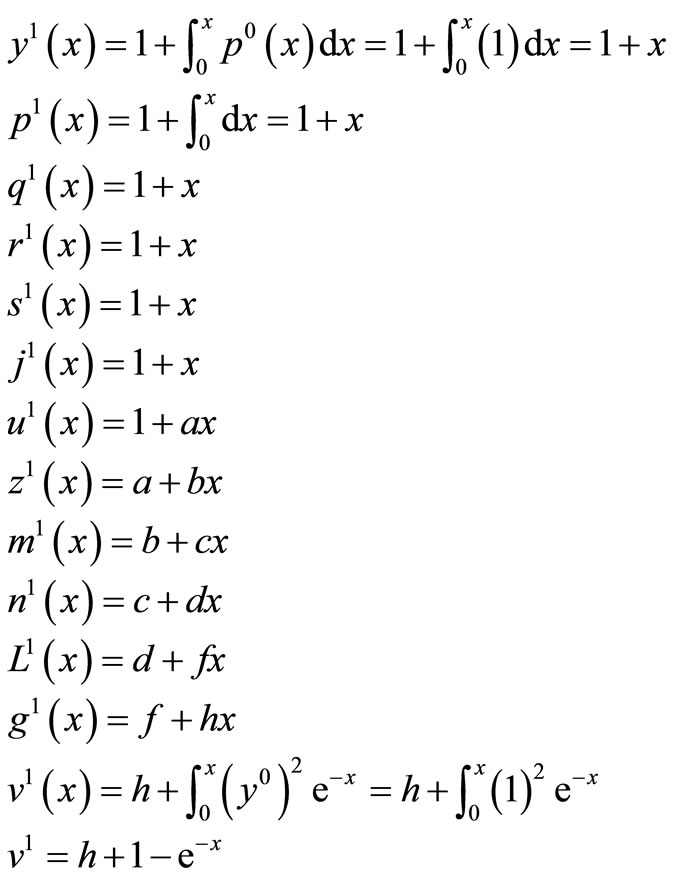

The solution is given as
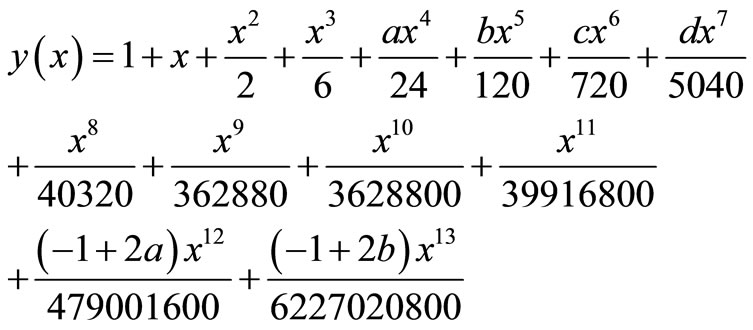 (18)
(18)
The coefficients  were obtained using MAPLE 13 with the boundary condition at
were obtained using MAPLE 13 with the boundary condition at  given
given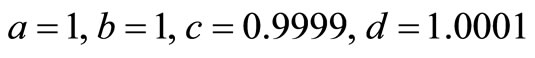 .
.
The series solution can thus be written as
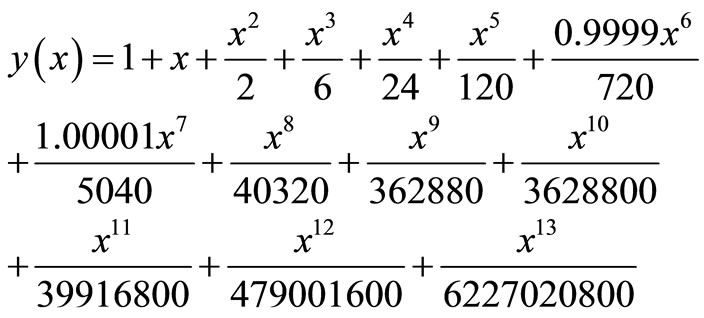 (19)
(19)
5. Results and Discussion
In example 1, Equation (13) is the numerical solution of Equation (7) using variational iteration technique. Table 1 below shows the listof the results obtained by Variational Iteration Method and compared with the Equation (8) which is the exact solution of Equation (7). As we see from Table 1; it is clear that the result obtained by the present method is very superior to that obtained by the exact solution with highly accurate. Also the exact solution and variational iteration method solution are depicted in Figure 1. As we see, there is a very good agreement between the approximate solution obtained by the eleventh iteration using variational iteration method and the exact solution which is shown in Table 1.
In example 2, the comparison of the exact solution with the series solution of the Equation (20), obtained using the variational iteration technique is shown in Table 2.

Table 1. Comparison of the exact solution with the series solution of the problem (7).

Table 2. Comparison of the exact solution with the series solution of the problem (14).

Figure 1. The graph show the exact and VIM solution for both Equation (8) and Equation (13) respectively.
The exact solution and the series solution obtained are depicted in Figure 2. There is a very good agreement and relationship between the series solution obtained by 13th iteration using variational iterations method and the exact solution which is shown in Table 2.
6. Conclusions
In this paper, variational iteration method has been successfully employed to obtain the approximate solutions of boundary value problem for thirteenth-order differential equations. The method is applied in a direct way without using linearization, transformation, discretization, perturbation or restriction assumptions. We concluded that the proposed technique is very powerful and efficient in finding the analytical solution for wide classes of boundary value problems.

Figure 2. The graph show the exact and VIM solution for both Equation (15) and Equation (20) respectively.
It is worthwhile mentioning that the method is capable of reducing the volume of the computational work as compared to the classical methods. This can be seen in Tables 1 and 2, where the exact solution agreed with the series solution generated by variatinal iteration method. The error estimation is generated as compared with the exact method. Both approaches can be seen clearly on Figures 1 and 2. The method is extremely simple to be used, and is accurate for solving nonlinear differential equation. Hence variational iteration method is a powerful tool to search for solutions of various linear and nonlinear boundary value problems.
REFERENCES
- A. M. Wazwaz, “The Variational Iteration Method: A Reliable Analytic Tool for Solving Linear and Nonlinear Wave Equations,” Computer and Mathematics with Applications, Vol. 54, No. 7-8, 2007, pp. 926-932. http://dx.doi.org/10.1016/j.camwa.2006.12.038
- M. Inc and D. J. Evans, “An Efficient Approach to Approximate Solutions of Eight-Order Boundary-Value Problems,” International Journal of Computer Mathematics, Vol. 81, No. 6, 2007, pp. 685-692. http://dx.doi.org/10.1080/0020716031000120809
- R. P. Agarwal, “Boundary Value Problems for HigherOrder Differential Equations,” World Scientific, Singapore, 1986. http://dx.doi.org/10.1142/0266
- S. Chandrasekhar, “Hydrodynamic Hydromagnetic Stability,” Clarendon Press, Oxford, New York, 1981.
- A Boutayeb E. H. Twizell and K. Djidjeli, “Numerical Methods for Eight-, Tenthand Twelfth-Order Eigenvalue Problems Arising in Thermal Instability,” Advances in Computational Mathematics, Vol. 2, No. 4, 1994, pp. 407- 436. http://dx.doi.org/10.1007/BF02521607
- J. H. He, “Approximate Analytical Solution for Seepage Flow with Fractional Derivatives in Porous Media,” Computer Methods in Applied Mechanics and Engineering, Vol. Vol. 167, No. 1-2, 1998, pp. 57-68. http://dx.doi.org/10.1016/S0045-7825(98)00108-X
- S. Elham, “Variational Iteration Method—A Kind of Nonlinear Analytical Technique: Some Examples,” International Journal of Non-Linear Mechanics, Vol. 34, No. 4, 1999, pp. 699-708. http://dx.doi.org/10.1016/S0020-7462(98)00048-1
- M. Yulita, “Variational Method for Outonomous Ordinary Differential Equations,” Applied Mathematics and Computation, Vol. 114, No. 2-3, 2000, pp. 115-123. http://dx.doi.org/10.1016/S0096-3003(99)00104-6
- A. S. Arife, “Variational Theory for Linear Magneto— Elasticity,” International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 2, No. 4, 2001, pp. 309- 316.
- L. M. Watson and M. R. Scott, “Solving Spline-Collocation Approximations to Nonlinear Two-Point Boundary Value Problems by a Homotopy Method,” Applied Mathematics and Computation, Vol. 24, No. 4, 1987, pp. 333-357. http://dx.doi.org/10.1016/0096-3003(87)90015-4
- G. R. Liu and T. Y. Wu, “Differential Quadrature Solutions of Eight-Order Boundary-Value Differential Equations,” Journal of Computational and Applied Mathematics, Vol. 145, No. 1, 1973, pp. 223-235. http://dx.doi.org/10.1016/S0377-0427(01)00577-5
- T. Mura, M. Inokuti and H. Sekine, “General Use of Lagrange Multiplier Innonlinear Mathematical Physics,” In: Variational Method in the Mech. of Solids, Pergamon Press, New York, 1978, pp. 156-162.
- H. A. Watts and M. R. Scott, “A Systematical Collection of Codes for Solving Two-Point BVPs, Numerical Methods for Differential Systems,” Academic Press, Waltham, 1976.
- M. R. Scott and H. A. Watts, “Computational Solutions of Linear Two-Point Boundary Value Problems via Orthonormalization,” SIAM Journal on Numerical Analysis, Vol. 14, No. 1, 1977, pp. 40-70. http://dx.doi.org/10.1137/0714004
- G. Akram, S. S. Siddiqi and S. Zaheer, “Solution of Eighth Order Boundary Value Problems Using Variational Iteration Technique,” Submitted in European Journal of Scientific Research, 2007.
- S. S. Siddiqi and G Akram, “Solutions of Tenth-Order Boundary Value Problems Using Eleventh Degree Spline,” Applied Mathematics and Computation, Vol. 185, No. 1, 2007, pp. 115-127.
- S.S Siddiqi and S. Zaheer, “Solutions of Tenth-Order Boundary Value Problems Using Non-Polynomial Spline Technique,” Applied Mathematics and Computation, Vol. 190, 1977, pp. 641-651.
- S. S. Siddiqi and E. H. Twizell, “Spline Solution of Linear Tenth-Order Boundary Value Problems,” International Journal of Computer Mathematics, Vol. 68, No. 3-4, 1998, pp. 345-362. http://dx.doi.org/10.1080/00207169808804701

