Applied Mathematics
Vol. 3 No. 4 (2012) , Article ID: 18882 , 5 pages DOI:10.4236/am.2012.34052
A Generalized Symbolic Thomas Algorithm
Mathematics Department, Faculty of Science, Mansoura University, Mansoura, Egypt
Email: m_elmikkawy@yahoo.com
Received February 4, 2012; revised March 1, 2012; accepted March 8, 2012
Keywords: Tridiagonal Matrices; LU Factorization; Linear Systems; DETGTRI Algorithm; Thomas Algorithm
ABSTRACT
The current paper is mainly devoted to construct a generalized symbolic Thomas algorithm that will never fail. Two new efficient and reliable computational algorithms are given. The algorithms are suited for implementation using computer algebra systems (CAS) such as Mathematica, Macsyma and Maple. Some illustrative examples are given.
1. Introduction
The 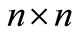 general tridiagonal matrix T takes the form:
general tridiagonal matrix T takes the form:
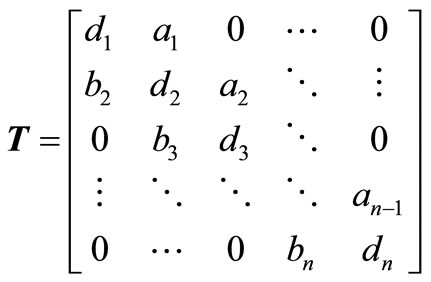 (1.1)
(1.1)
This type of matrices frequently appear in many scientific and engineering applications. This area of research is still very active and has been considered by many authors. The interested reader may refer to, for instance to [1-3] and the references therein. The 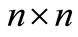 general tridiagonal matrix T in (1.1) can be stored using only three n-dimensional vectors since there is no need to store the zero elements. In this paper we shall focus on k-tridiagonal matrices [4] of order
general tridiagonal matrix T in (1.1) can be stored using only three n-dimensional vectors since there is no need to store the zero elements. In this paper we shall focus on k-tridiagonal matrices [4] of order 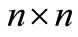 of the form:
of the form:
 (1.2)
(1.2)
where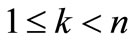 . For
. For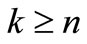 , the matrix in (1.2) is a diagonal matrix and the case k = 1 gives the ordinary tridiagonal matrix in (1.1). As pointed out in [4,5], the matrix
, the matrix in (1.2) is a diagonal matrix and the case k = 1 gives the ordinary tridiagonal matrix in (1.1). As pointed out in [4,5], the matrix 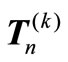 plays an important role in describing generalized k-Fibonacci numbers. Furthermore, the matrix
plays an important role in describing generalized k-Fibonacci numbers. Furthermore, the matrix 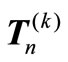 has very recently received attention by some authors. In [5], using direct sum of matrices, it is proved that det
has very recently received attention by some authors. In [5], using direct sum of matrices, it is proved that det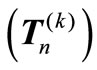 may be obtained as the product of exactly k ordinary tridiagonal matrices of the form (1.1) and this can be done using the efficient symbolic algorithm DETGTRI in [6]. The motivation of the present paper is to continue the study of the LU factorization [7] of the matrix
may be obtained as the product of exactly k ordinary tridiagonal matrices of the form (1.1) and this can be done using the efficient symbolic algorithm DETGTRI in [6]. The motivation of the present paper is to continue the study of the LU factorization [7] of the matrix 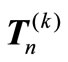 in (1.2) using a new approach, different from the recent approach given in [8], in order to obtain a generalized symbolic Thomas algorithm that will never fail.
in (1.2) using a new approach, different from the recent approach given in [8], in order to obtain a generalized symbolic Thomas algorithm that will never fail.
The organization of the paper is as follows. In Section 2, generalization of the DETGTRI algorithm in [6] is investigated. The generalization of the Thomas algorithm [7] is considered in Section 3. Some illustrative examples are given in Section 4 for the sake of illustration. A conclusion is given in Section 5.
2. Generalization of the DETGTRI Algorithm
We begin this section by giving the following result whose proof will be omitted.
Theorem 2.1. For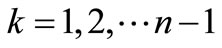 , the Doolittle LU factorization [7] of the k-tridiagonal matrix
, the Doolittle LU factorization [7] of the k-tridiagonal matrix 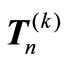 in (1.2) is given by:
in (1.2) is given by:
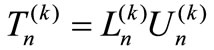 , (2.1)
, (2.1)
where
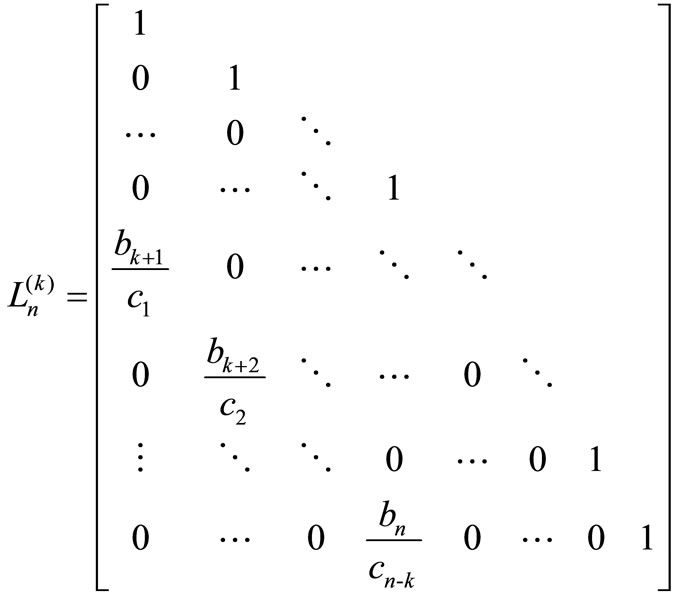 (2.2)
(2.2)
and
 (2.3)
(2.3)
with
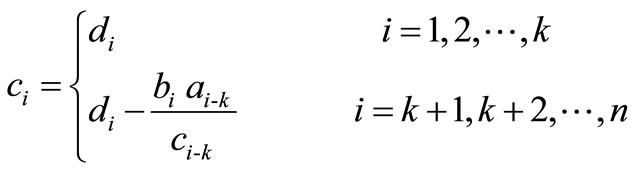 (2.4)
(2.4)
Now we can formulate our first result.
Algorithm 2.1. (Generalization of the DETGTRI algorithm [6])
To compute the determinant of the k-tridiagonal matrix 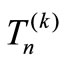 in (1.2) we may proceed as follows:
in (1.2) we may proceed as follows:
Step 1: Compute 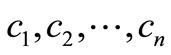 to its simplest rational forms according to (2.4), setting
to its simplest rational forms according to (2.4), setting 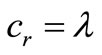 (
(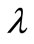 is just a symbolic name) whenever
is just a symbolic name) whenever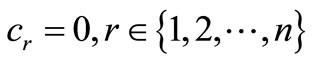 .
.
Step 2: Compute the polynomial 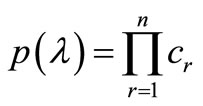 to its simplest rational form. Meanwhile, det
to its simplest rational form. Meanwhile, det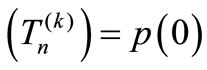 .
.
The Algorithm 2.1 will be referred to as k-DETGTRI algorithm. The DETGTRI algorithm in [6] is a special case of the k-DETGTRI algorithm when k = 1. Note that the k-DETGTRI algorithm computes det in linear time.
in linear time.
3. Generalization of the Thomas Numeric Algorithm
In this section, we are going to generalize the wellknown Thomas numeric algorithm [7]. The purpose of the generalized algorithm is to solve the following linear system for any .
.
The new algorithm can be stated as follows:
Algorithm 3.1. (Generalization of the Thomas numeric algorithm [7])
To solve the linear system of the form (3.1), we may proceed as follows:
Step 1: Compute 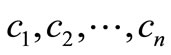 using (2.4).
using (2.4).
Step 2: Compute 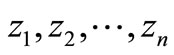 using
using
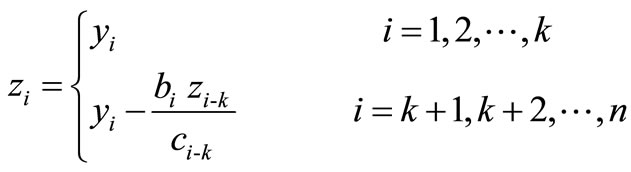
Step 3: The solution of the system (3.1) is
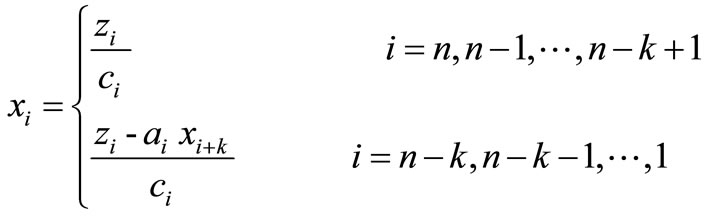
The Algorithm 3.1 will be referred to as k-Thomas algorithm. The Thomas algorithm is a special case of the k-Thomas algorithm when k = 1.
Note 3.1. Since the k-Thomas algorithm is based on the LU factorization of the matrix,  , then the kThomas numeric algorithm may fail if
, then the kThomas numeric algorithm may fail if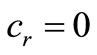 ,
,
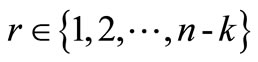 as can be seen from (2.1)-(2.4). To remove all cases in which the k-Thomas numeric algorithm fails, it is convenient to give the following symbolic version of the k-Thomas numeric algorithm described above. The k-Thomas symbolic algorithm can be stated as follows:
as can be seen from (2.1)-(2.4). To remove all cases in which the k-Thomas numeric algorithm fails, it is convenient to give the following symbolic version of the k-Thomas numeric algorithm described above. The k-Thomas symbolic algorithm can be stated as follows:
Algorithm 3.2. (Generalized symbolic Thomas algorithm)
To solve the linear system of the form (3.1), we may proceed as follows:
Step 1: Compute 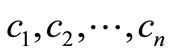 to its simplest rational forms using (2.4), setting
to its simplest rational forms using (2.4), setting  (
(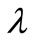 is just a symbolic name) whenever
is just a symbolic name) whenever .
.
Step 2: Compute 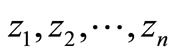 to its simplest rational forms using:
to its simplest rational forms using:

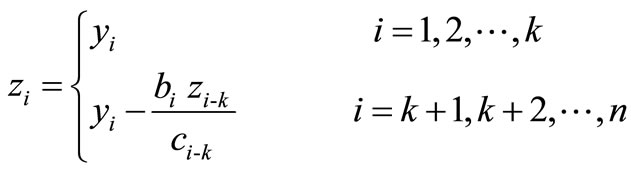
Step 3: The solution of the system (3.1) is

evaluated at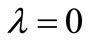 .
.
Before we consider the solution of the system (3.1) by using the k-Thomas algorithm, it is recommended to use the k-DETGTRI algorithm to check the nonsingularity of the coefficient matrix  firstly.
firstly.
4. Some Illustrative Examples
In this section we are going to give some illustrative examples.
Example 4.1. Consider the following k-tridiagonal system with n = 10 and k = 4:
 (4.1)
(4.1)
Applying the numeric or the symbolic version of the k-Thomas algorithms gives:
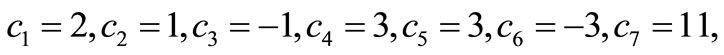
 (Step 1);
(Step 1); Hence det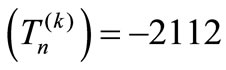 . Thus
. Thus  is nonsingular.
is nonsingular.
• 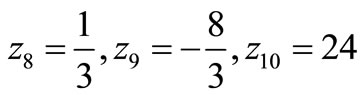
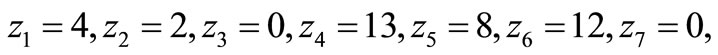 (Step 2);
(Step 2);
• 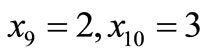
 (Step 3).
(Step 3).
Example 4.2. Consider the following k-tridiagonal system with n = 10 and k = 4 (this example is Example 4.1 with slight modifications in some positions. The modified positions are written in bold):
 (4.2)
(4.2)
In this case the k-Thomas numeric algorithm fails since 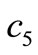 = 0 as can be easily checked. However, the k-Thomas symbolic algorithm yields:
= 0 as can be easily checked. However, the k-Thomas symbolic algorithm yields:
• 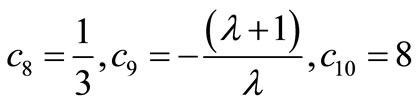
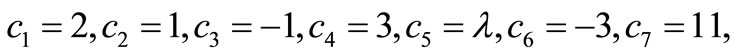 (Step 1);
(Step 1);
Hence det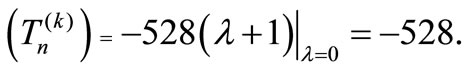 Consequently the matrix
Consequently the matrix 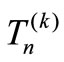 is nonsingular.
is nonsingular.
• 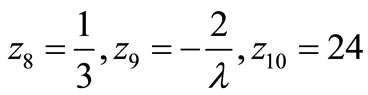
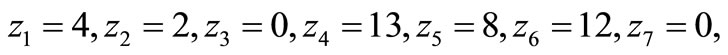 (Step 2);
(Step 2);
• 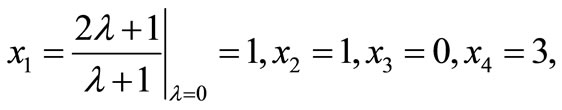
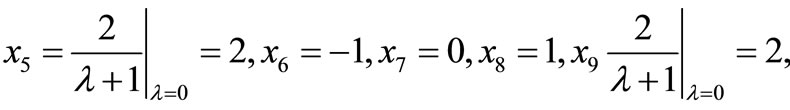
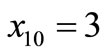 (Step 3).
(Step 3).
Example 4.3. Consider the k-tridiagonal matrix
 (4.3)
(4.3)
For this matrix, the k-DETGTRI algorithm gives:
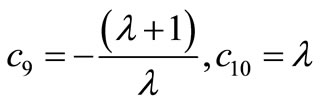
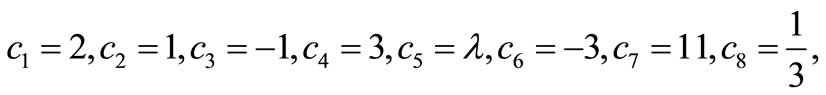 . (Step 1)
. (Step 1)
Hence 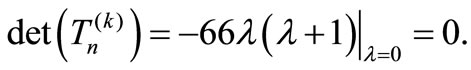 Therefore the matrix
Therefore the matrix  is singular.
is singular.
5. Conclusion
A generalized symbolic Thomas algorithm, that will never fail, is developed, for the first time, in this paper. The algorithm is suited for implementation using the Computer Algebra Systems (CAS) such as Macsyma, Maple and Mathematica.
REFERENCES
- M. E. A. El-Mikkawy, “A Note on a Three-Term Recurrence for a Tridiagonal Matrix,” Applied Mathematics and Computation, Vol. 139, No. 2-3, 2003, pp. 503-511. doi:10.1016/S0096-3003(02)00212-6
- M. E. A. El-Mikkawy, “On the Inverse of a General Tridiagonal Matrix,” Applied Mathematics and Computation, Vol. 150, No. 3, 2004, pp. 669-679. doi:10.1016/S0096-3003(03)00298-4
- M. E. A. El-Mikkawy and A. Karawia, “Inversion of General Tridiagonal Matrices,” Applied Mathematics Letters, Vol. 19, No. 8, 2006, pp. 712-720. doi:10.1016/j.aml.2005.11.012
- M. El-Mikkawy and T. Sogabe, “A New Family of k-Fibonacci Numbers,” Applied Mathematics and Computation, Vol. 215, No. 12, 2010, pp. 4456-4461. doi:10.1016/j.amc.2009.12.069
- T. Sogabe and M. El-Mikkawy, “Fast Block Diagonalization of k-Tridiagonal Matrices,” Applied Mathematics and Computation, Vol. 218, No. 6, 2011, pp. 2740-2743. doi:10.1016/j.amc.2011.08.014
- M. E. A. El-Mikkawy, “A Fast Algorithm for Evaluating nth Order Tridiagonal Determinants,” Journal of Computational and Applied Mathematics, Vol. 166, No. 2, 2004, pp. 581-584. doi:10.1016/j.cam.2003.08.044
- R. L. Burden and J. D. Faires, “Numerical Analysis,” 7th Edition, Books & Cole Publishing, Pacific Grove, 2001.
- A. Yalciner, “The LU Factorization and Determinants of the k-Tridiagonal Matrices,” Asian-European Journal of Mathematics, Vol. 4, No. 1, 2011, pp. 187-197. doi:10.1142/S1793557111000162

