Applied Mathematics
Vol. 3 No. 5 (2012) , Article ID: 19055 , 9 pages DOI:10.4236/am.2012.35067
Effect of Non-Uniform Temperature Gradient on the Onset of Rayleigh-Bénard Electro Convection in a Micropolar Fluid
Department of Mathematics, Christ University, Bangalore, India
Email: {pranesh.s, riya.baby}@christuniversity.in
Received December 28, 2011; revised March 19, 2012; accepted March 26, 2012
Keywords: Micropolar Fluid; Rayleigh Number; Electro Convection; Non-Uniform Temperature Gradients; Galerkin Technique
ABSTRACT
The effects of electric field and non-uniform basic temperature gradient on the onset of Rayleigh-Bénard convection in a micropolar fluid are studied using the Galerkin technique. The eigenvalues are obtained for free-free, rigid-free and rigid-rigid velocity boundary combinations and for isothermal and/or adiabatic temperature boundaries. The microrotation is assumed to vanish at the boundaries. A linear stability analysis is performed. The influence of various micropolar fluid parameters and electric Rayleigh number on the onset of convection has been analyzed. One linear and five non-uniform temperature profiles are considered and their comparative influence on onset is discussed.
1. Introduction
Electrohydrodynamics can be regarded as a branch of fluid mechanics concerned with electrical force effects. It can also be considered as that part of electrodynamics, which is involved with the influence of moving media on electric fields. Actually, it is both of these areas combined, since many of the most interesting problems in electrohydrodynamics involve both an effect of fluid motion on the fields and an influence of the fields on the motion. Onset of natural convection in the presence of an external field such as a magnetic field or an electric field has been studied extensively. In highly conductive fluids magnetic effects will be dominant. To the contrary, in dielectric fluids with low values of the conductivity, the electric effects will essentially govern the motion. The forces that are exerted by an electric field on free charges present in a liquid are transmitted by collision to the neutral molecules. The fluid will be set in motion, thus changing the distribution of charges that in turn modifies the electric field: there is an analogy between the Rayleigh-Bénard instability and pure electroconvection. In the latter case, the destabilizing force is proportional to the mean charge gradient. The effect of electric fields on the motion of liquids is employed in the electrohydrodynamic energy converters devices in which the electric field energy is directly converted into the kinetic energy of a liquid flow. Another technical application is related to the possibility of intensifying or suppressing the heat and mass transfer in high-voltage devices and, in some cases, to the ability of controlling such processes. Onset of convection in a dielectric fluid layer in the presence of electric field has been studied by Roberts [1], Maekawa, Abe and Tanasawa [2], Char and Chiang [3], Douiebe et al. [4], El-Sayed [5], Rudraiah and Gayathri [6], Hemalatha and Shivakumara [7].
The theory of micropolar fluid introduced by Eringen [8] have become an important field of research especially in many industrially important fluids like paints, polymeric suspensions, colloidal fluids, and also in physiological fluids such as normal human blood and synovial fluids. The mathematical theory of equations of micropolar fluids and applications of these fluids in the theory of lubrication and porous media is presented by Lukaszewicz [9].
The Rayleigh-Bénard instability in a horizontal thin layer of fluid heated from below is an important particular stability problem. The theory of thermomicropolar convection heated from below was studied by many authors Datta and Sastry [10], Ahmadi [11], Bhattacharya and Jena [12], Siddheshwar and Pranesh [13-17] and more recently by Pranesh and Kiran [18].
In many of the heat transfer problems, control (suppress or augment) of convection plays a vital role. There are several mechanisms that can be used effectively to control convection, namely by applying magnetic/electric field externally or by coriolis force due to rotation or by maintaining non-uniform temperature gradient. The literature pertaining to maintaing non-uniform temperature gradient in micropolar fluid encompassing the above mechanisms is mainly concerned with magnetic field or rotation and a corresponding study for micropolar fluid with effect of electric field is missing despite its importance in understanding control of convection encountered in many scientific and technological problems.
The aim of this paper is to analyze the influence of various non-uniform basic temperature gradients on the onset of electroconvection in a layer of micropolar fluid. The eigenvalue of the problem is solved numerically using the Galerkin technique.
2. Mathematical Formulation
Consider an infinite horizontal layer of a Boussinesquian, electrically conducting fluid, of depth “d” permeated by an externally applied uniform electric field normal to the layer (see Figure 1). A cartesian co-ordinate system is taken with origin in the lower boundary and z-axis vertically upwards. Let DT be the temperature difference between the upper and lower boundaries. The body forces acting on the fluid are buoyancy and electric field.
The governing equations for the Rayleigh-Bénard situation in a micropolar fluid are Continuity equation:
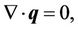 (1)
(1)
Conservation of linear momentum:
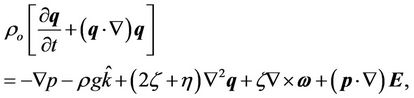 (2)
(2)
Conservation of angular momentum:
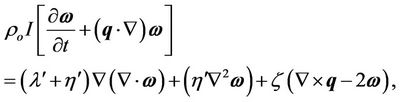 (3)
(3)

Figure 1. Schematic diagram of Rayleigh-Bénard situation for a fluid with suspended particles.
Conservation of energy:
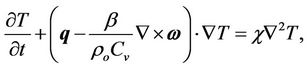 (4)
(4)
Equation of state:
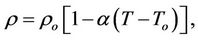 (5)
(5)
Equation of state for dielectric constant:
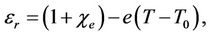 (6)
(6)
Faraday’s law:
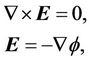 (7)
(7)
Equation of polarization field:
 (8)
(8)
where, 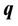 is the velocity,
is the velocity, 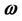 is the spin,
is the spin, 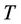 is the temperature,
is the temperature, 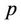 is the hydrodynamic pressure,
is the hydrodynamic pressure, 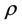 is the density,
is the density,  is the density of the fluid at reference temperature
is the density of the fluid at reference temperature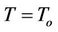 , g is the acceleration due to gravity,
, g is the acceleration due to gravity, 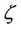 is the coupling viscosity coefficient or vortex viscosity,
is the coupling viscosity coefficient or vortex viscosity, 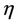 is the shear kinematic viscosity co-efficient, I is the moment of inertia,
is the shear kinematic viscosity co-efficient, I is the moment of inertia, 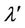 and
and 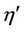 are the bulk and shear spin viscosity coefficients,
are the bulk and shear spin viscosity coefficients,  is the micropolar heat conduction coefficient,
is the micropolar heat conduction coefficient,  is the specific heat,
is the specific heat, 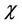 is the thermal conductivity,
is the thermal conductivity, 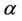 is the co-efficient of thermal expansion,
is the co-efficient of thermal expansion, 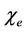 is thermal susceptibility,
is thermal susceptibility, 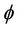 is the electrostatic potential,
is the electrostatic potential, 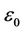 is electric permeability of free space,
is electric permeability of free space, 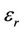 is dielectric constant,
is dielectric constant, 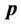 is dielectric polarization,
is dielectric polarization, 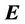 is electric field.
is electric field.
The basic state of the fluid being quiescent is described by:
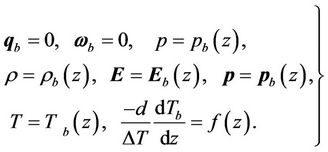 (9)
(9)
The monotonic, non-dimensional basic temperature gradient f(z) which is non-negative satisfies the condition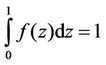 . The non-uniformity in Tb as in (9) finds its origin in transient heating or cooling at the boundaries (Siddheshwar and Pranesh [14,15] and references therein). We have considered various reference steady-state temperature gradients in this paper and these are defined below:
. The non-uniformity in Tb as in (9) finds its origin in transient heating or cooling at the boundaries (Siddheshwar and Pranesh [14,15] and references therein). We have considered various reference steady-state temperature gradients in this paper and these are defined below:
Equations (1)-(8) in the basic state specified by Equation (9) becomes:
 (10).
(10).
We now superpose infinitesimal perturbations on the quiescent basic state and study the instability. Let the basic state be disturbed by an infinitesimal thermal perturbation. We now have:
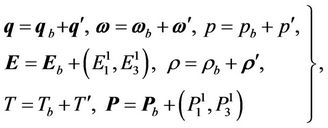 (11)
(11)
The primes indicate that the quantities are infinitesimal perturbations and subscript “b” indicates basic state value.
From Equation (8), on linearization yields
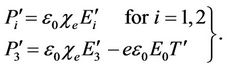 (12)
(12)
The second equation of (7) implies one can write  where
where 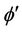 is the perturbed electric scalar potential. Introducing the electric potential
is the perturbed electric scalar potential. Introducing the electric potential 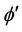 and substituting Equation (11) into Equations (1)-(8) and using the basic state solution (10), we get linearised equation governing the infinitesimal perturbations in the form:
and substituting Equation (11) into Equations (1)-(8) and using the basic state solution (10), we get linearised equation governing the infinitesimal perturbations in the form:
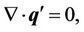 (13)
(13)
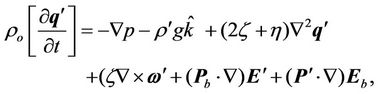 (14)
(14)
 (15)
(15)
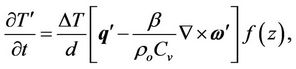 (16)
(16)
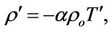 (17)
(17)
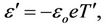 (18)
(18)
 (19)
(19)
Using Equation (17) in (14), operating curl twice on the resulting equation, operating curl on Equation (15), using Equation (12) on Equation (19) and non dimensionalised all the equation using the following definition
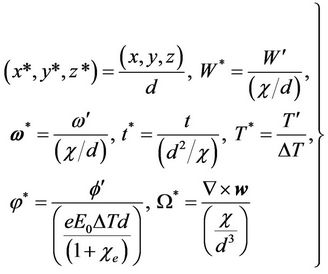 (20).
(20).
we get,
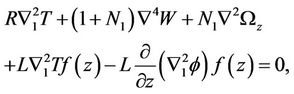 (21)
(21)
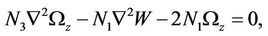 (22)
(22)
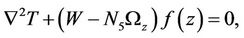 (23)
(23)
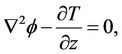 (24)
(24)
where the asterisks have been dropped for simplicity and the non-dimensional parameters 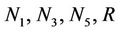 and L are as defined as
and L are as defined as
 (Rayleigh number),
(Rayleigh number),
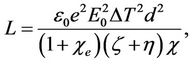 (Electric number),
(Electric number),
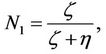 (Coupling Parameter),
(Coupling Parameter),
 (Couple Stress Parameter),
(Couple Stress Parameter),
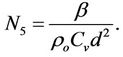 (Micropolar Heat Conduction parameter).
(Micropolar Heat Conduction parameter).
The infinitesimal perturbation 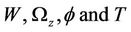 are assumed to be periodic waves and hence these permit a normal mode solution in the form (See Chandrashekar [16]).
are assumed to be periodic waves and hence these permit a normal mode solution in the form (See Chandrashekar [16]).
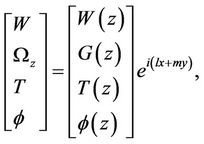 (25)
(25)
where l and m are horizontal components of the wave number a.
Substituting Equation (25) into Equations (21)-(24), we get
 , (26)
, (26)
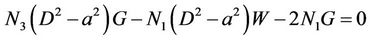 , (27)
, (27)
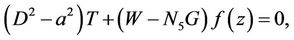 (28)
(28)
 (29)
(29)
where 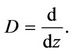
The sets of ordinary differential Equations (26)-(29) are solved using Galerkin technique. Multiplying Equation (26) by W, Equation (27) by G, Equation (28) by T and Equation (29) by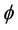 , integrating the resulting equation by parts with respect to z from 0 to 1 and taking W = AW1 , G = BG1, T = CT1 and
, integrating the resulting equation by parts with respect to z from 0 to 1 and taking W = AW1 , G = BG1, T = CT1 and  in which A, B, C and E are constants with W1, G1, T1 and
in which A, B, C and E are constants with W1, G1, T1 and 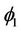 are trial functions. This procedure yields the following equation for the Rayleigh number R:
are trial functions. This procedure yields the following equation for the Rayleigh number R:
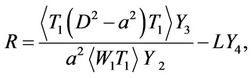 (30)
(30)
where

In the Equation (30),  denotes integration with respect to z between
denotes integration with respect to z between 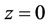 and
and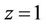 . We note here that R in Equation (30) is a functional and the EulerLagrange equations for the extremisation of R are Equations (26) to (29).
. We note here that R in Equation (30) is a functional and the EulerLagrange equations for the extremisation of R are Equations (26) to (29).
The value of critical Rayleigh number depends on the boundaries, and it is obtained for the following boundary combinations:
a) Free-free isothermal/adiabatic, no spin.
b) Rigid-rigid isothermal/adiabatic, no spin.
c) Rigid-free isothermal/adiabatic, no spin.
3. Results and Discussions
In this paper, we have studied the effect of non-uniform basic temperature gradient on the onset of Rayleigh-Bé- nard convection in a micropolar fluid in the presence of electric field. One uniform and five non-uniform basic temperature gradients are chosen for study (See Table 1). Keeping in mind the laboratory and geophysical problems, the following type of boundaries have been investigated:
1) Free-Free 2) Rigid-Rigid 3) Rigid-Free.
These boundaries may be either isothermal or adiabatic.
It is observed for the symmetric boundary combinations, Rc1 = Rc5 = Rc6 ≠ Rc4 and Rc2 = Rc3 ≠ Rc4. On the basis of this following grouping of non-uniform temperature profiles can be made for free-free and rigid-rigid boundaries (symmetric boundaries).
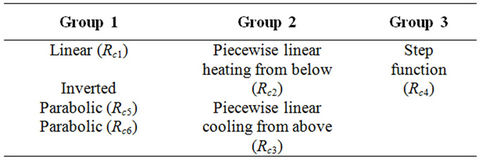
Rci (i = 1 6) in the table are the critical Rayleigh numbers corresponding to the six basic temperature gradients. In the case of rigid-free boundaries (non-symmetric boundary combination) no two Rci are the same. In the non-symmetric case we find that Rc4 < Rc3 < Rc2 < Rc6 < Rc1 < Rc5. In the case of piecewise linear and step function profiles, the critical Rayleigh number Rc depends on the thermal depth ε, in addition to depending on the parameters of the problem (See Table 2). The values of the micropolar parameters are taken according to Clausius – Duhem inequality (see [13]).
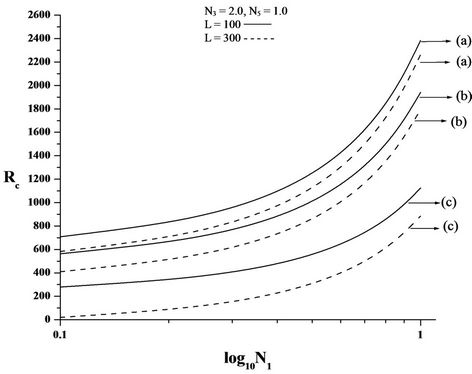
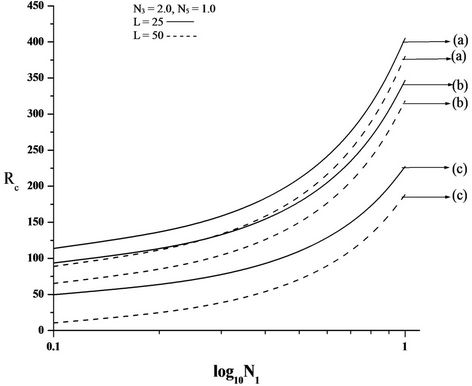
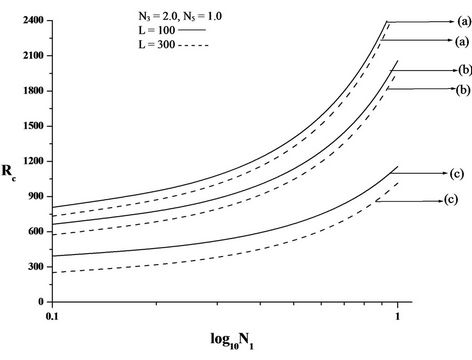
Figures 2(A)-4(A) are the plots of critical Rayleigh number Rc versus coupling parameter N1 for free-free,

Table 1. Non-uniform basic temperature gradients.
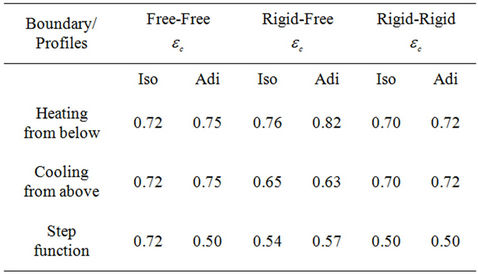
Table 2. The value of the thermal depth 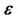 for N1 = 0.1, N3 = 2.0, N5 = 1.0, L = 100. Isothermal (Iso) and Adiabatic (Adi).
for N1 = 0.1, N3 = 2.0, N5 = 1.0, L = 100. Isothermal (Iso) and Adiabatic (Adi).
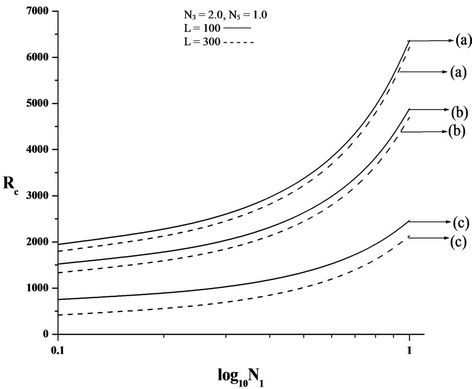
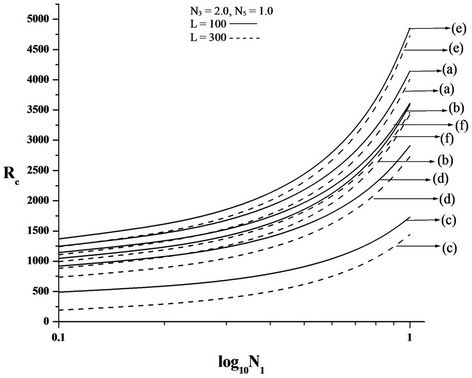
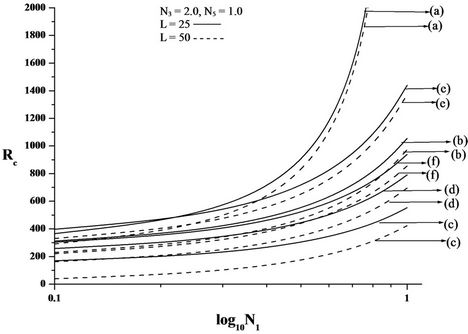
rigid-rigid, rigid-free isothermal boundaries respectively for different values of electric number L and for different non-uniform basic temperature gradients. It is observed that as N1 increases, Rc increases. Increase in N1 indicates the increase in the concentration of the microelements. These microelements consume the greater part of the energy in developing gyrational velocity and as a result the onset of convection is delayed. From this we conclude that an increase in N1 is to stabilise the system.
Figures 2(B)-4(B) are the plots of critical Rayleigh number Rc versus couple stress parameter N3 for free-free, rigid-rigid, rigid-free isothermal boundaries respectively for different values of electric number L and for different non-uniform basic temperature gradients. We note that the role played by the shear stress in the conservation of linear momentum is played by couple stress in the conservation of angular momentum equation. It is observed that as N3 increases Rc decreases. Because, when N3 increases the couple stress of the fluid increases, this increase in the couple stress causes the micro-rotation to decrease. Therefore, increase in N3 destabilises the system. From the figure it is observed that decrease in Rc is significant for lower values of N3 and at higher values, the dip in Rc is insignificant. From this we conclude that couple stress are operative at only small values of N3.
Figures 2(C)-4(C) are the plots of critical Rayleigh number Rc versus micropolar heat conduction parameter N5 for free-free, rigid-rigid, rigid-free isothermal boundaries respectively for different values of electric number L and for different non-uniform basic temperature gradient. When N5 increases, the heat induced into the fluid due to these microelements also increases, thus reducing the heat transfer from bottom to top. The decrease in heat transfer is responsible for delaying the onset of instability. We conclude that an, increase in N5 increases Rc and thereby stabilises the system.
From the Figures, it is also observed that the increase in electric Rayleigh number L, layer becomes more and more unstable. Thus, the effect of electric field is to
 (a)
(a)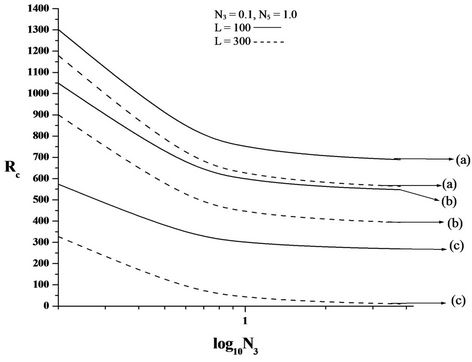 (b)
(b)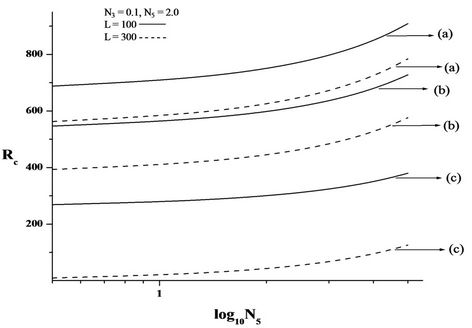 (c)
(c)
Figure 2. Plot of critical Rayleigh number Rc versus (A) coupling parameter, N1, (B) couple stress parameter, N3, (C) micropolar heat conduction parameter, N5, for free-free isothermal boundaries, for different non-uniform temperature gradient and for different electric Rayleigh number L. (a) Linear temperature profile; (b) Heating from below; (c) Step function.
 (a)
(a) (b)
(b)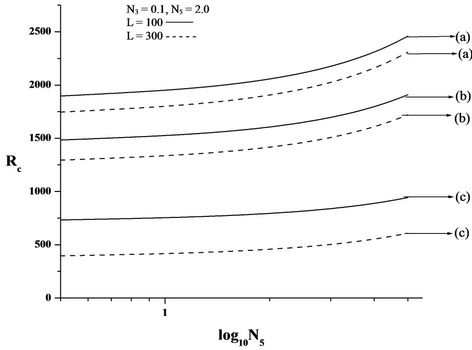 (c)
(c)
Figure 3. Plot of critical Rayleigh number Rc versus (A) coupling parameter, N1, (B) couple stress parameter, N3, (C) micropolar heat conduction parameter, N5, for rigid-rigid isothermal boundaries, for different non-uniform temperature gradient and for different electric Rayleigh number L. (a) Linear temperature profile; (b) Heating from below; (c) Step function.
 (a)
(a)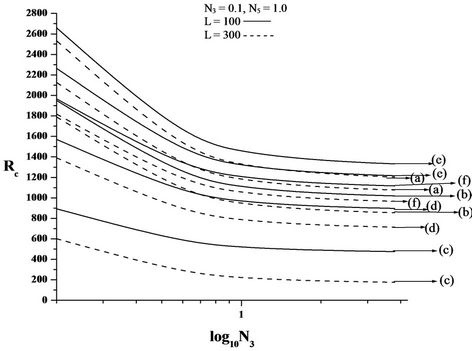 (b)
(b)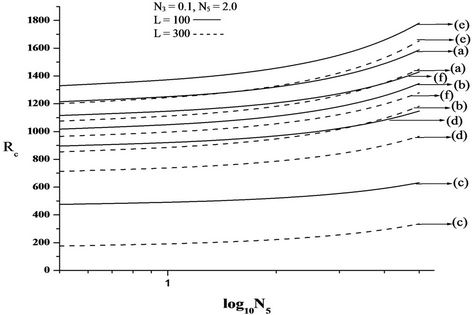 (c)
(c)
Figure 4. Plot of critical Rayleigh number Rc versus (A) coupling parameter, N1, (B) couple stress parameter, N3, (C) micropolar heat conduction parameter, N5, for rigid-free isothermal boundaries, for different non-uniform temperature gradient and for different electric Rayleigh number L. (a) Linear temperature profile; (b) Heating from below; (c) Step function; (d) Cooling from below; (e) Inverted parabolic; (f) Parabolic.
augment the onset of convection.
From the present study we recover the following results as a limiting case:
1) When L = 0, N1 = 0 results of Chandrashekhar [19].
2) When L = 0, N1 ≠ 0, results of Siddheshwar and Pranesh [11].
3) When L ≠ 0, N1 = 0, f(z) = 1, results of Turnbull [20].
Figures 5-7 are plots for adiabatic boundaries corresponding to Figures 2-4 of isothermal boundaries. The results of adiabatic boundaries are qualitatively similar to that of isothermal boundaries. However, it is found that the Rc with respect to adiabatic boundary is less than the corresponding Rc in isothermal boundaries.
The effect of N1, N3, and N5 on Rc is true both in the presence and absence of electric field. On the other hand, when the micro rotation and electric field are simultaneously present the stabilizing effect of N1 is being reduced, being counteracted by the electric field.
It has also been found that the critical wave number for stationary convection is, in general, insensitive to the changes in the micropolar parameters but is influenced by the electric field. A strong electric field succeeds in inducing only the coupling parameter N1 into influencing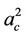 . We also find that
. We also find that 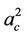 decreases with electric field. Thus, electric field increases the dimension of the cell.
decreases with electric field. Thus, electric field increases the dimension of the cell.
4. Conclusions
Following conclusions are drawn from the present study:
1) Stationary convection is the preferred mode of instability in a micropolar fluid.
2) Rayleigh-Bénard convection in Newtonian fluids may be delayed by adding micron sized suspended particles.
3) The combined effect of electric field and coupling parameter is to reinforce together and to accelerate the onset of convection when compared in their individual influence on the instability.
4) By choosing appropriate non-uniform basic temperature profile it is possible to control the RayleighBénard convection.
5) The step function is the most destabilizing basic temperature distribution and inverted parabolic is the most stabilizing basic temperature distribution.
6) Implication of the present investigation is that by controlling the magnitude of electric field and choosing the appropriate non-uniform basic temperature gradient it is possible to control convective instability in the micropolar fluid layer.
5. Acknowledgements
This work is funded by Research Department (Major Research Project), Christ University, Bangalore. Authors
 (a)
(a) (b)
(b)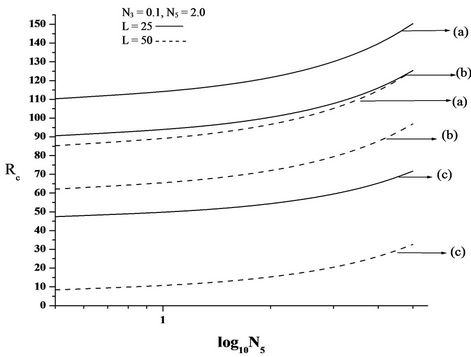 (c)
(c)
Figure 5. Plot of critical Rayleigh number Rc versus (A) coupling parameter, N1, (B) couple stress parameter, N3, (C) micropolar heat conduction parameter, N5, for free-free adiabatic boundaries, for different non-uniform temperature gradient and for different electric Rayleigh number L. (a) Linear temperature profile; (b) Heating from below; (c) Step function.
 (a)
(a)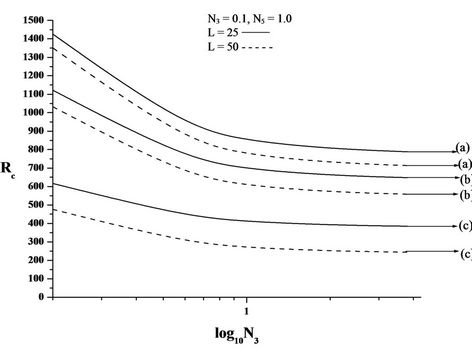 (b)
(b)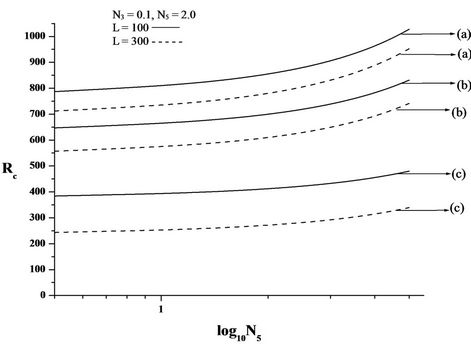 (c)
(c)
Figure 6. Plot of critical Rayleigh number Rc versus (A) coupling parameter, N1, (B) couple stress parameter, N3, (C) micropolar heat conduction parameter, N5, for rigid-rigid adiabatic boundaries, for different non-uniform temperature gradient and for different electric Rayleigh number L. (a) Linear temperature profile; (b) Heating from below; (c) Step function.
 (a)
(a)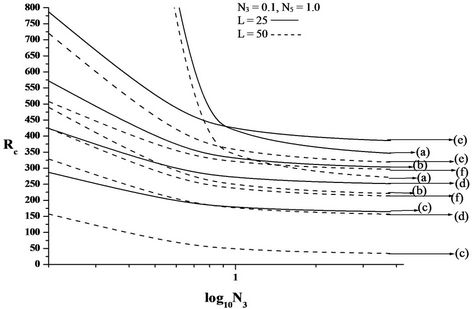 (b)
(b) (c)
(c)
Figure 7. Plot of critical Rayleigh number Rc versus (A) coupling parameter, N1, (B) couple stress parameter, N3, (C) micropolar heat conduction parameter, N5, for rigid-free adiabatic boundaries, for different non-uniform temperature gradient and for different Electric number L. (a) Linear temperature profile; (b) Heating from below; (c) Step function; (d) Cooling from below; (e) Inverted parabolic; (f) Parabolic.
would like to acknowledge Management of Christ University for their support in completing the work.
REFERENCES
- P. H. Roberts, “Electrodynamic Convection,” Quarterly Journal of Mechanics and Applied Mathematics, Vol. 22, No. 2, 1969, pp. 211-220. doi:10.1093/qjmam/22.2.211
- T. Maekawa, K. Abe and I. Tanasawa, “Onset of Natural Convection under an Electric Field,” International Journal of Heat and Mass Transfer, Vol. 35, 1992, pp. 613- 621.
- M. I. Char and K. T. Chiang, “Boundary Effects on the Bénard-Marangoni Instability under the Electric Field,” Applied Scientific Research, Vol. 52, No. 4, 1994, pp. 331-354. doi:10.1007/BF00936836
- A. Douiebe, M. Hannaoui, G. Lebon, A. Benaboud and A. Khmou, “Effects of a.c. Electric Field and Rotation on Bénard-Marangoni Convection,” Flow, Turbulence and Combustion, Vol. 67, No. 3, 2001, pp. 185-204. doi:10.1023/A:1015038222023
- M. F. El-Sayed, “Onset of Electroconvective Instability of Oldroydian Viscoelastic Liquid Layer in Brinkman Porous Medium,” Archive of Applied Mechanics, Vol. 78, No. 3, 2008, pp. 211-224. doi:10.1007/s00419-007-0153-x
- N. Rudraiah and M. S. Gayathri, “Effect of Thermal Modulation on the Onset of Electrothermoconvection in a Dielectric Fluid Saturated Porous Medium,” Journal of Heat Transfer, Vol. 131, No. 10, 2009, p. 101009. doi:10.1115/1.3180709
- K. Hemalatha and I. S. Shivakumara, “Thermo Convective Instability in a Heat Generating Dielectric Fluid Layer under Alternating Current Electric Field,” Carmelight, Vol. 7, 2010, pp. 125-136.
- A. C. Eringen, “Theory of Micropolar Fluids,” International Journal of Engineering Science, Vol. 16, 1966, p. 1.
- G. Lukaszewicz, “Micropolar Fluid Theory and Applications,” Birkhauser, Boston, 1999.
- B. Datta and V. U. K. Sastry, “Thermal Instability of a Horizontal Layer of Micropolar Fluid Heated from Below,” International Journal of Engineering Science, Vol. 14, No. 7, 1976, pp. 631-637. doi:10.1016/0020-7225(76)90005-7
- G. Ahmadi, “Stability of a Micropolar Fluid Layer Heated from Below,” International Journal of Engineering Science, Vol. 14, No. 7, 1976, pp. 81-89. doi:10.1016/0020-7225(76)90058-6
- S. P. Bhattacharyya and S. K. Jena, “On the Stability of Hot Layer of Micropolar Fluid,” International Journal of Engineering Science, Vol. 21, No. 9, 1983, pp. 1019-1024. doi:10.1016/0020-7225(83)90043-5
- P. G. Siddheshwar and S. Pranesh, “Magnetoconvection in a Micropolar Fluid,” International Journal of Engineering Science, Vol. 36, No. 10, 1998, pp. 1173-1181. doi:10.1016/S0020-7225(98)00013-5
- P. G. Siddheshwar and S. Pranesh, “Effects of a NonUniform Basic Temperature Gradient on Rayleigh-Bénard Convection in a Micropolar Fluid,” International Journal of Engineering Science, Vol. 36, No. 11, 1998, pp. 1183-1196. doi:10.1016/S0020-7225(98)00015-9
- P. G. Siddheshwar and S. Pranesh, “Effects of Non-Uniform Temperature Gradients and Magnetic Field on the Onset of Convection in Fluids with Suspended Particles under Microgravity Conditions,” Indian Journal of Engineering and Materials Sciences, Vol. 8, No. 77, 2001, pp. 83.
- P. G. Siddheshwar and S. Pranesh, “Magnetoconvection in Fluids with Suspended Particles under 1g and mg,” International Journal of Aerospace Science and Technology, Vol. 6, No. 2, 2001, pp. 105-114.
- P. G. Siddheshwar and S. Pranesh, “Linear and Weakly Non-Linear Analyses of Convection in a Micropolar Fluid,” Hydrodynamics VI-Theory and Applications, 2005, pp. 487-493.
- S. Pranesh and R. V. Kiran, “Study of Rayleigh Bénard Magneto Convection in a Micropolar Fluid with Maxwell-Cattaneo Law,” Applied Mathematics, Vol. 1, 2010, pp. 467-480.
- S. Chandrasekhar, “Hydrodynamic and Hydromagnetic Stability,” Clarendon Press, Oxford, 1961.
- R. J. Turnbull, “Electro Convective Instability with a Stabilizing Temperature Gradient, I. Theory,” Physics of Fluids, Vol. 11, No. 12, 1968, pp. 2588-2596.

