Applied Mathematics
Vol. 3 No. 1 (2012) , Article ID: 16767 , 6 pages DOI:10.4236/am.2012.31007
Some Kinds of Sheaf Control Problems for Control Systems
Faculty of Mathematics and Computer Science, Vietnam National University, Ho Chi Minh City, Vietnam
Email: *ndphu_dhtn@yahoo.com.vn
Received November 8, 2011; revised December 20, 2011; accepted December 27, 2011
Keywords: Control Systems; Sheaf Solutions; Control Theory
ABSTRACT
Recently, the field of differential equations has been studying in a very abstract method. Instead of considering the behaviour of one solution of a differential equation, one studies its sheaf-solutions in many kinds of properties, for example, the problems of existence, comparison, … of sheaf solutions. In this paper we study some of the problems of controllability for sheaf solutions of control systems.
1. Introduction
In [1-4] the authors have investigated sheaf solutions of control differential equations in the fields: comparison of sheaf solutions in the cases’ two admissible controls 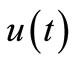 and
and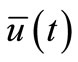 , and some initial conditions
, and some initial conditions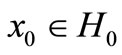 ,
, 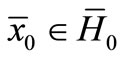 , where the Hausdorff distance between the sets of initials
, where the Hausdorff distance between the sets of initials  and
and  is enough small.
is enough small.
The problems of sheaf controllability and sheaf optimization are still open. The present paper is organized as follows. In Section 2, we review some facts about sheaf solutions. In Section 3 we give many kinds of sheaf control problems, of sheaf controllability optimal problems.
2. Preliminaries
In n-dimension Euclidian space  usually we have considered the control systems (CS):
usually we have considered the control systems (CS):
 (2.1)
(2.1)
where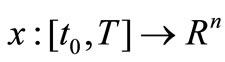 ,
, 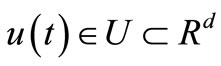
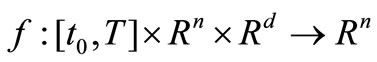 . A solution to CS (2.1) is represented by:
. A solution to CS (2.1) is represented by:
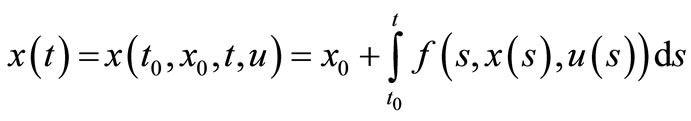 (2.2)
(2.2)
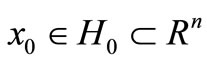 ,
, 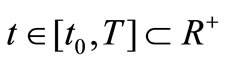 ,
,  is a collection of some given initials.
is a collection of some given initials.
Definition 2.1. We say that a control 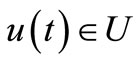 is admissible, if:
is admissible, if:
1) 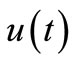 satisfies (2.2) for all
satisfies (2.2) for all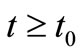 ;
;
2) 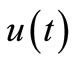 is bounded by norm
is bounded by norm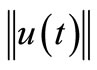 .
.
That means the functions  are measurable (integrable) satisfiying almost everywhere on
are measurable (integrable) satisfiying almost everywhere on  the relationships (2.1) and (2.2), then
the relationships (2.1) and (2.2), then  is called the trajectory of the CS (2.1) and
is called the trajectory of the CS (2.1) and 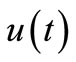 is called the control. Therefore, we shall always understand a pair of functions
is called the control. Therefore, we shall always understand a pair of functions 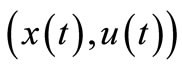 interrelated by the relationship (2.1) and (2.2). It is clear that several controls
interrelated by the relationship (2.1) and (2.2). It is clear that several controls  can correspond to one
can correspond to one 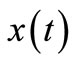 trajectory and if CS (2.1) has a nonunique solution, then several trajectory
trajectory and if CS (2.1) has a nonunique solution, then several trajectory  can correspond to one control
can correspond to one control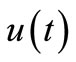 .
.
Definition 2.2. A state pair 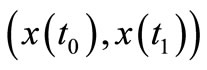 of solutions of control systems (2.1) will be a controllable if after time
of solutions of control systems (2.1) will be a controllable if after time 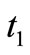 we shall find a control
we shall find a control 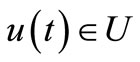 such that:
such that:
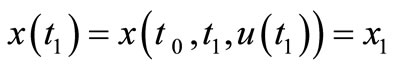 (2.3)
(2.3)
Definition 2.3. A control system (2.1) is said to be:
(GC) global controllable if every state pair of set solution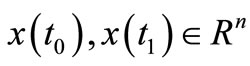 .
.
(GA) global achievable if for every 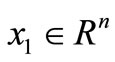 we have a state pair of solutions
we have a state pair of solutions 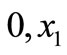 that is GC.
that is GC.
(GAZ) global achievable to zero if for every 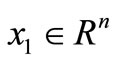 we have a state pair
we have a state pair 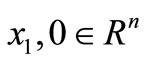 that will be controlable.
that will be controlable.
In [2] the authors have compared the sheaf solutions for set control differential equations (SCDEs).
In [4] the author has study the problems (GC), (GA) and (GAZ) for set control differential equations (SCDEs).
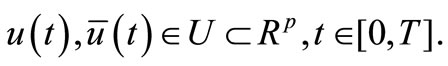
Definition 2.4. A sheaf solution (or sheaf trajectory)  is denoted by a number of solutions that make into sheaves (lung one on top of the other and often tied together) for all
is denoted by a number of solutions that make into sheaves (lung one on top of the other and often tied together) for all :
:
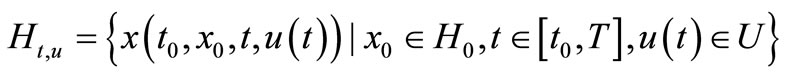 (2.4)
(2.4)
Definition 2.5. A cut-set (a cross-area) of sheaf solution 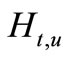 at time
at time 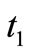 is denoted by:
is denoted by:
 (2.5)
(2.5)
3. Main Results
Let’s consider again the control systems (CS):
 (3.1)
(3.1)
where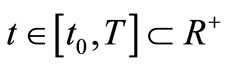 ,
, 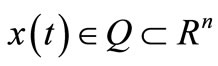 , Q is a compact set in
, Q is a compact set in  and
and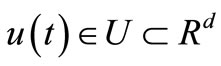 —admissible controls. Assume that for CS (3.1) there exists solution (2.2) and sheaf solution (2.4).
—admissible controls. Assume that for CS (3.1) there exists solution (2.2) and sheaf solution (2.4).
We will need the following hypotheses on the data of control problem for CS (3.1):
(Hf1): 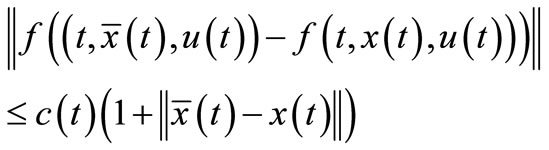
(Hf2): 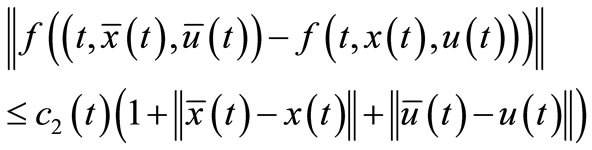
where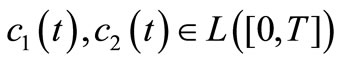 .
.
Assume that at all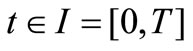 ,
, 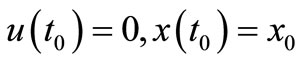 for two admissible controls
for two admissible controls  we have two forms of sheaf solutions:
we have two forms of sheaf solutions:
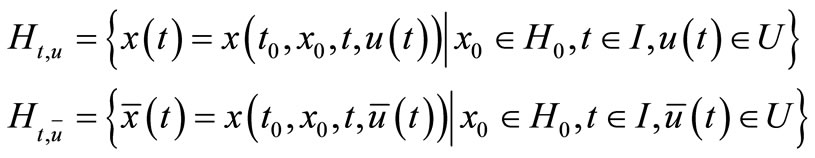 (3.2)
(3.2)
where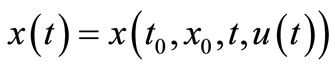 —solution of CS (2.1) (see Figure 1).
—solution of CS (2.1) (see Figure 1).
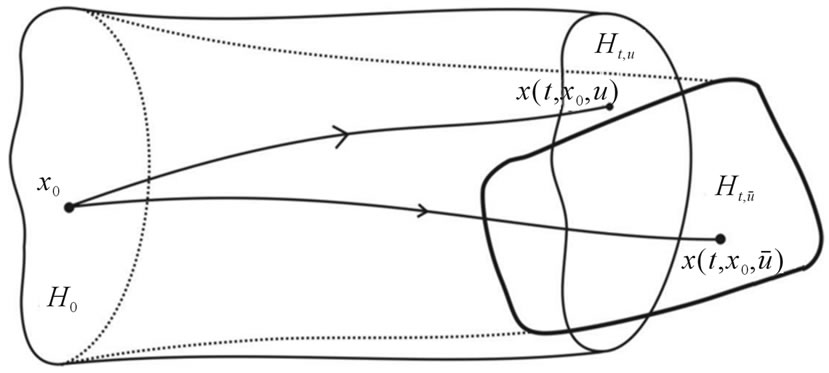
Figure 1. The sheaf solutions of CS (2.1) in two admissible controls.
Definition 3.1. The Hausdorff distance between set 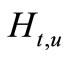 and
and 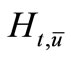 is denoted by:
is denoted by:

Definition 3.2. The pair of the any sets 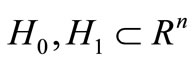 will be controllable if after time
will be controllable if after time  we shall find a control
we shall find a control 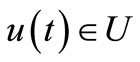 and one map
and one map 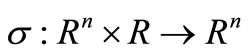 such that:
such that:
 (3.3)
(3.3)
Theorem 3.1. Under Hypothes (Hf1), let 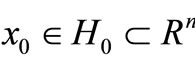 —is initial, any set
—is initial, any set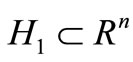 . The pair of the sets
. The pair of the sets 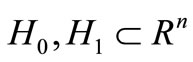 will be controllable if:
will be controllable if:
1)  belongs to solutions of CS (3.1), and 2)
belongs to solutions of CS (3.1), and 2) 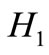 is cut-set of sheaf solution to (3.1), that means
is cut-set of sheaf solution to (3.1), that means
 .
.
Proof. If 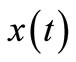 belongs to solutions of CS(3.1) then it is
belongs to solutions of CS(3.1) then it is
 .
.
For any 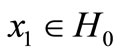 we have a pair
we have a pair 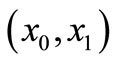 that is controllable, because
that is controllable, because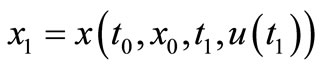 , where
, where 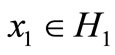 —cut-set of sheaf solutions with
—cut-set of sheaf solutions with
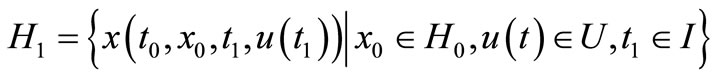
As in results, we have one map moving 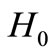 to
to 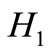 that means
that means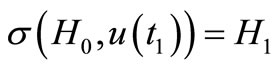 .
.
Definition 3.3. The control system (3.1) is said to be:
(SC1) sheaf controllable in type 1, if for all , there exists
, there exists 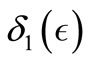 and admissible controls
and admissible controls 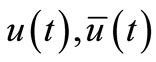 that satisfy
that satisfy 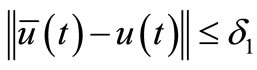 then
then
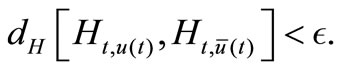 (3.4)
(3.4)
(SC2) sheaf controllable in type 2 for any admissible control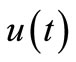 , if for all
, if for all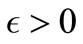 , there exists
, there exists 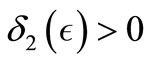 such that the initials
such that the initials 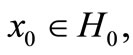
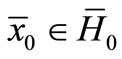 with
with 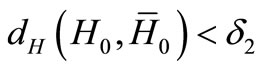 then
then
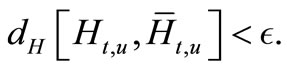 (3.5)
(3.5)
(SC3) sheaf controllable in type 3, if for all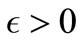 , there exist
, there exist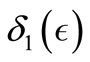 ,
, 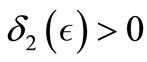 such that the initials
such that the initials 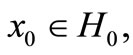
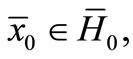 with
with 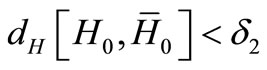 and for any admissible controls
and for any admissible controls  that satisfy
that satisfy 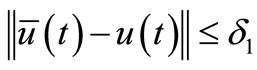 then
then
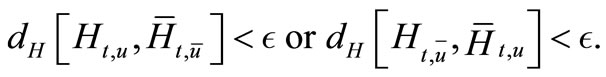 (3.6)
(3.6)
Lemma 3.1. Under Hypothes (Hf1), for all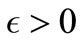 , there exists
, there exists 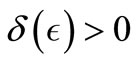 if control system (3.1) with:
if control system (3.1) with:
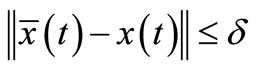
then two cut -sets of sheaf-solutions of CS (3.1) satisfy an estimate:
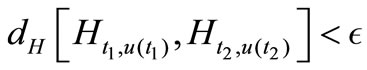 (3.7)
(3.7)
Proof. Suppose that for CS (3.1) the right hand side 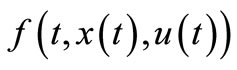 satisfies (Hf1) then there exists unique solution
satisfies (Hf1) then there exists unique solution 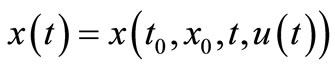 which satisfies (2.2).
which satisfies (2.2).
If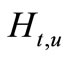 —sheaf solution of CS (3.1) then for admissible control
—sheaf solution of CS (3.1) then for admissible control  we have the cut-sets at any times
we have the cut-sets at any times , that satisfy estimate (3.7):
, that satisfy estimate (3.7):
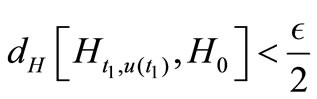 and
and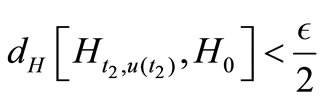 .
.
We have
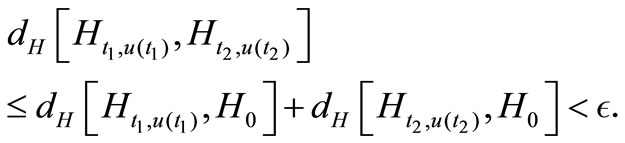

Theorem 3.2. Assume that, under Hypothes (Hf2), the admissible controls 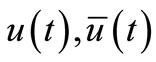 that satisfy
that satisfy 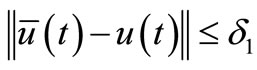 , then CS (3.1) is sheaf-controllable SC1.
, then CS (3.1) is sheaf-controllable SC1.
Proof. Suppose that for CS (3.1) the right hand side  satisfies (Hf2) then there exists unique solution
satisfies (Hf2) then there exists unique solution  which satisfies (2.2).
which satisfies (2.2).
If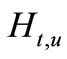 —sheaf solution of CS (3.1) then for admissible control
—sheaf solution of CS (3.1) then for admissible control  we have the cut-sets at every times
we have the cut-sets at every times , that satisfy estimate (3.7):
, that satisfy estimate (3.7):  and
and .
.
We have

as results the CS (3.1) is sheaf-controllable SC1. 
Corollary 3.1. If CS (3.1) is SC1, the right hand side 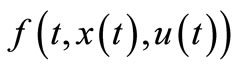 satisfies condition of lemma 3.1 then for all
satisfies condition of lemma 3.1 then for all 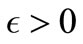 there exists
there exists 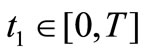 such that:
such that:
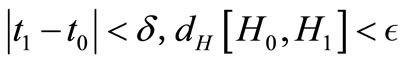
Proof. Because solution of CS (3.1) is equivalent: 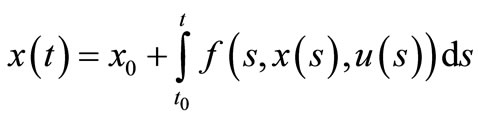 then
then
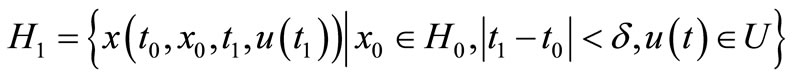
by lemma 3.1 we have: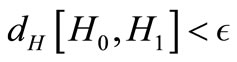

Theorem 3.3. Under hypothes (Hf1), assume that the initials 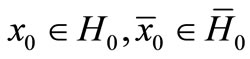 for all
for all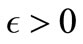 , there exists
, there exists 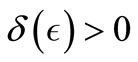 such that:
such that: 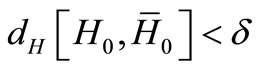 then for any admissible control
then for any admissible control 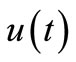 we have:
we have:
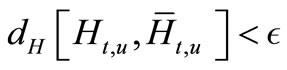
that means CS (3.1) is sheaf controllable CS2.
Proof. We have estimate
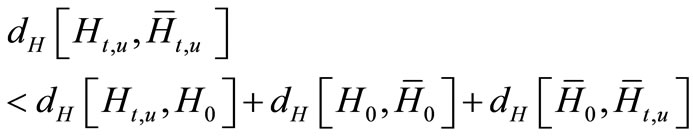
For all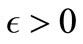 ,
, 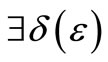 such that
such that 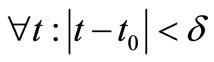
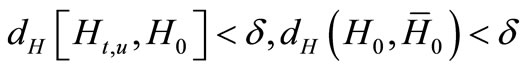 and
and
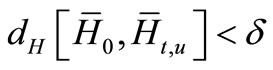 choosing
choosing  then we have
then we have . As results imply that CS (3.1) is SC2.
. As results imply that CS (3.1) is SC2. 
Theorem 3.4. Under Hypothes (Hf2), assume that for all 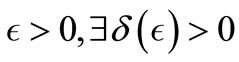 and satisfy the followings:
and satisfy the followings:
1) 
2) then for any admissible controls
then for any admissible controls 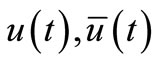 we have:
we have:
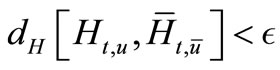
that means CS (3.1) is sheaf controllable CS3.
Proof. Beside (2.4) for 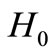 and
and 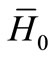 we have:
we have:
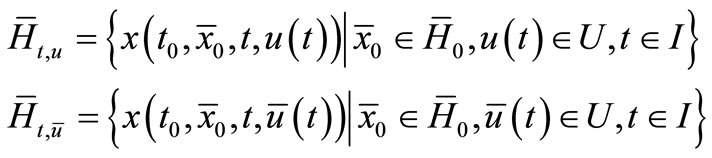
and estimate 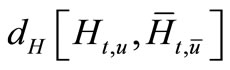 as following:
as following:
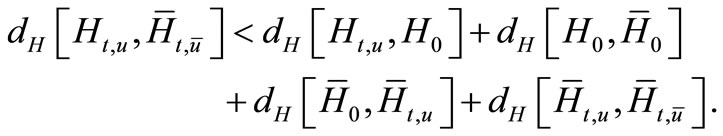
Choosing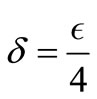 , we have:
, we have:
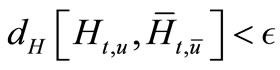

Definition 3.4. We say that for control system (3.1) are given OCP—the optimization control problem if it denotes:
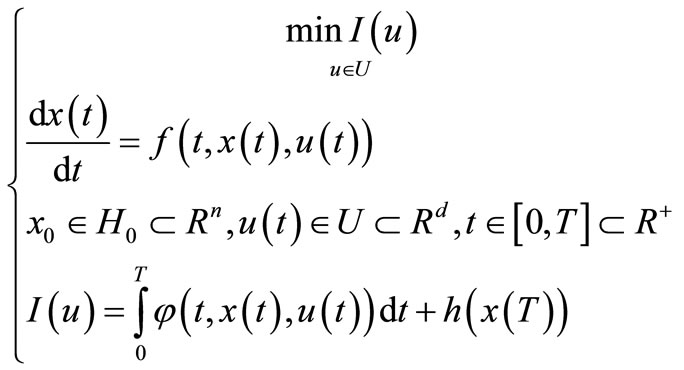 (3.8)
(3.8)
where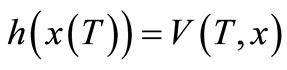 , such that V(T,x) is solution to Hamillton Jacobi Bellman (HJB)—partial differential equation:
, such that V(T,x) is solution to Hamillton Jacobi Bellman (HJB)—partial differential equation:
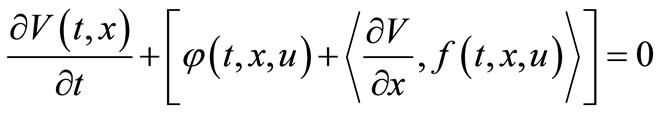 (3.9)
(3.9)
We have to find the optimal control  for OCP (3.8).
for OCP (3.8).
Lemma 3.1. In optimization control problems (3.8) if 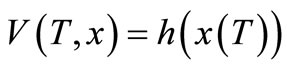 then
then 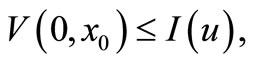
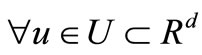
Proof. Putting 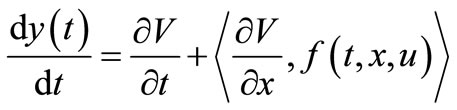
we have integral for all :
:

Because
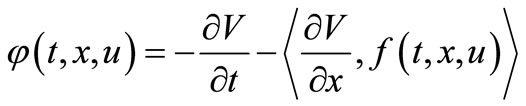
impilies that
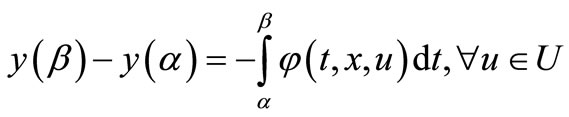
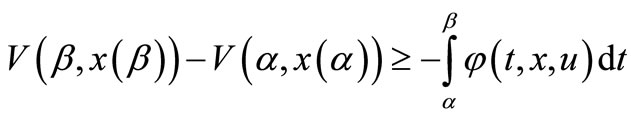
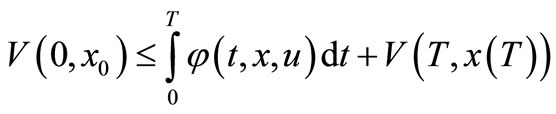
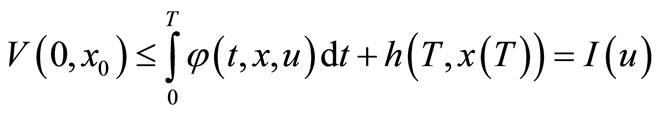

Theorem 3.5. Assume that OCP (3.8) has  and there exists feedback
and there exists feedback 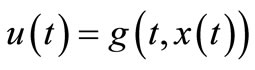 such that:
such that:

then exists optimal control 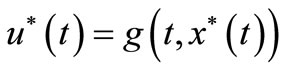 for OCP (3.8).
for OCP (3.8).
Proof. Assume that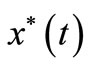 —one of solutions of control systems (3.1) such that
—one of solutions of control systems (3.1) such that 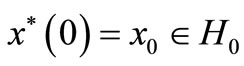 there exists feedback
there exists feedback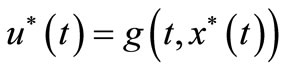 :
:
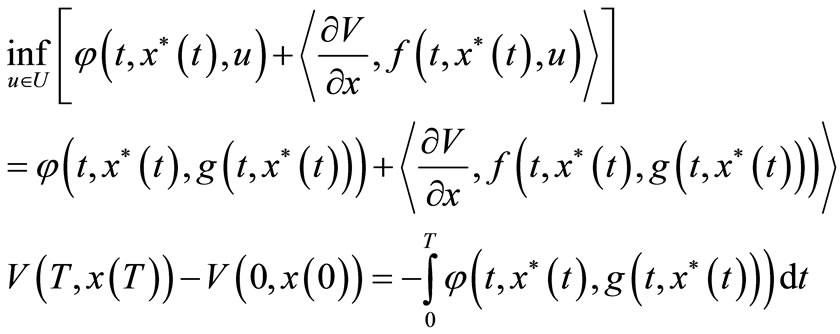
By lemma 3.3 we have
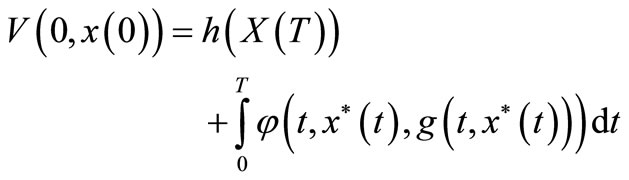
such that —optimal control for OCP (3.8).
—optimal control for OCP (3.8). 
Definition 3.5. We say that for control system (3.1) are given SOCP—the sheaf-optimization control problem if it denotes:
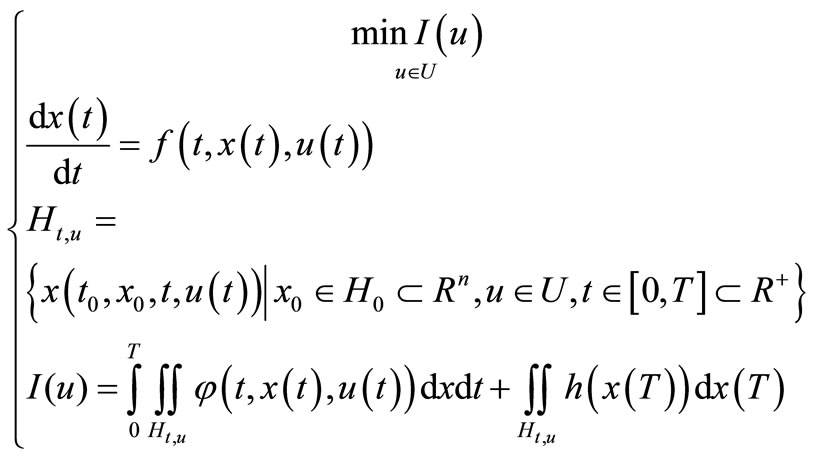 (3.10)
(3.10)
where —integral on
—integral on 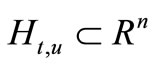 and
and
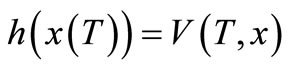 such that
such that 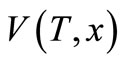 is solution to (HJB)—partial differential equation:
is solution to (HJB)—partial differential equation:
 (3.11)
(3.11)
Lemma 3.2. Assume that V(t, x) is a solution of HJB partial differential equation (3.10) with the boundary conditions:

If function
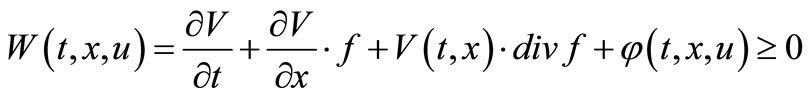
and u(t) is admissible control then for optimization control problem SOCP (3.10) there exists estimate:
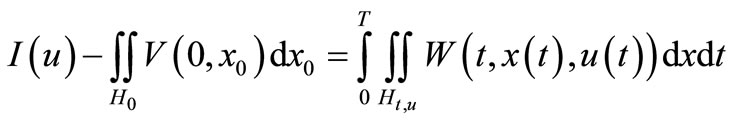
Proof. Putting
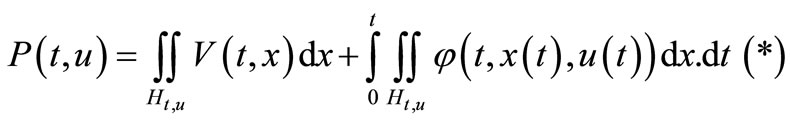
we have:
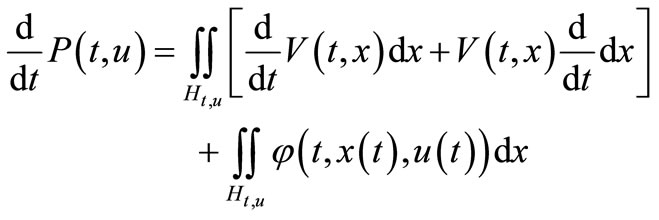
 where
where 
then
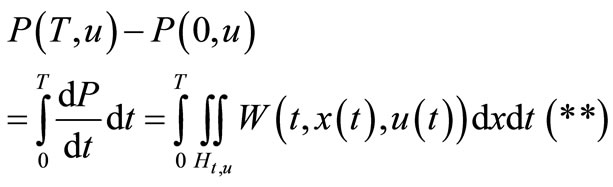
By (*) we have

and  then (**) impilies that
then (**) impilies that
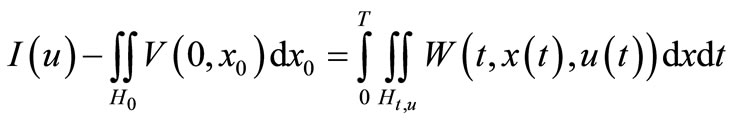

Theorem 3.6. (Necessary Conditions)
Assume that SOCP (3.10) has solution, that means there exists optimal control 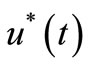 such that
such that
 and
and  is a solution of HJBpartial differential equation (3.11) then the necessary conditions for this SOCP (3.10) are:
is a solution of HJBpartial differential equation (3.11) then the necessary conditions for this SOCP (3.10) are:
1) 
2)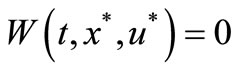 , where
, where
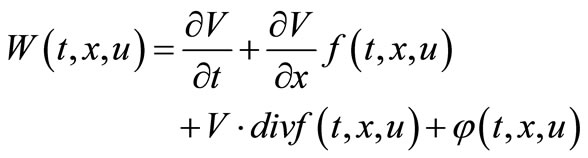
Proof. Suppose that a function SOCP (3.10) that means
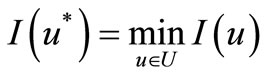 . Because V(t, x)-solution of HJBpartial differential equation (3.11):
. Because V(t, x)-solution of HJBpartial differential equation (3.11):
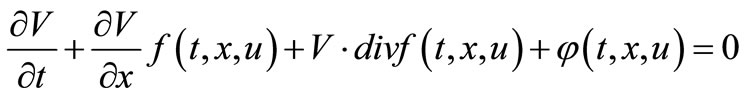
with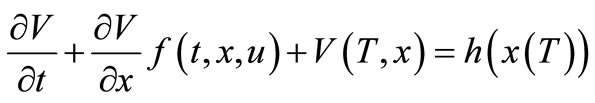 if function
if function 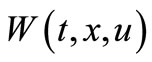 satisfies:
satisfies:
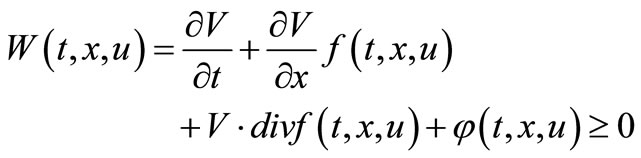
that integrable on sheaf solutions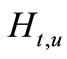 .
.
By lemma 3.2, if 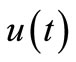 is admissible control then for optimization control problem SOCP (3.10) there exists estimate:
is admissible control then for optimization control problem SOCP (3.10) there exists estimate:
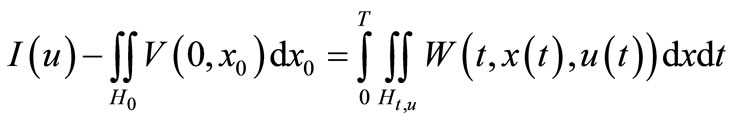
Assume that for SOCP (3.10) has optimal control  then for all
then for all , we have
, we have 

Theorem 3.7. (Sufficient Conditions)
Assume that  any admissible control for SOCP (3.10) and
any admissible control for SOCP (3.10) and  is a solution of HJB-partial differential Equation (3.11) then the sufficient conditions for this SOCP (3.10) are:
is a solution of HJB-partial differential Equation (3.11) then the sufficient conditions for this SOCP (3.10) are:
1) 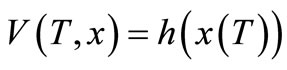
2) 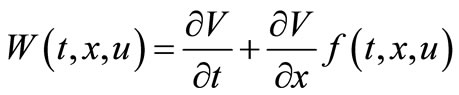
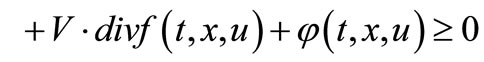
3) there exists 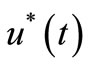 such that
such that
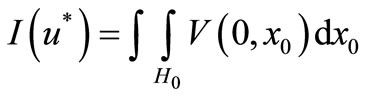
Proof. There exists the other admissible control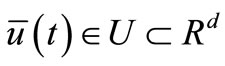 , such that for SOCP (3.10) we have
, such that for SOCP (3.10) we have
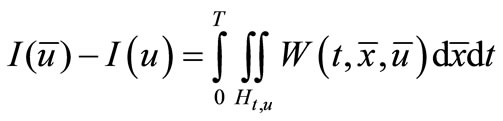
By condition (1) of theorem 3.6 we have a function
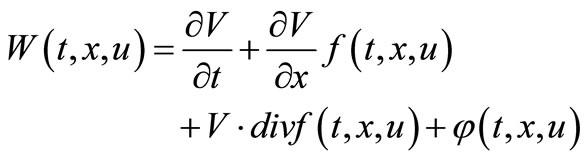
that integrable on sheaf solutions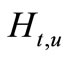 .
.
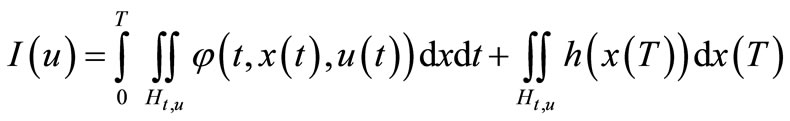
We find the function 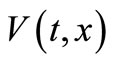 from equation:
from equation:
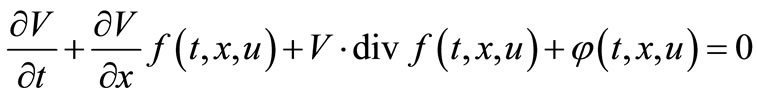
with condition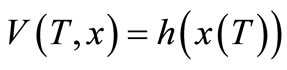 .
.
By condition (2) of this theorem:
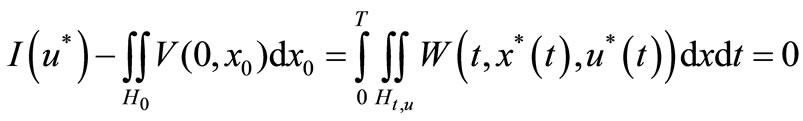
and implies that —optimal control for SOCP (3.10).
—optimal control for SOCP (3.10). 
Example 3.1. When using missiles not for the purpose of shooting down aircraft noise bomb attack as B52 shot if only 01 or 02 rockets can not succeed. The rockets theit fire it will be the interference or escort aircraft will be explosive.
A problem arises: What to do in order to shoot down aircraft noise when operating in the sky. To solve this problem, we must fire simultaneously from SAM sites from 03 or more results. The rockets have to be controlled from headquarters and shot to pick the exact point-B52.
Mathematical model for problem shooting attack aircraft noise control system with (3.10), the test bundle (2.4) and optimization problem are (SOCP) in the above with n = 3 (see Figure 2).
4. Conclusions
The Sheaf Optimization problem for Control Systems
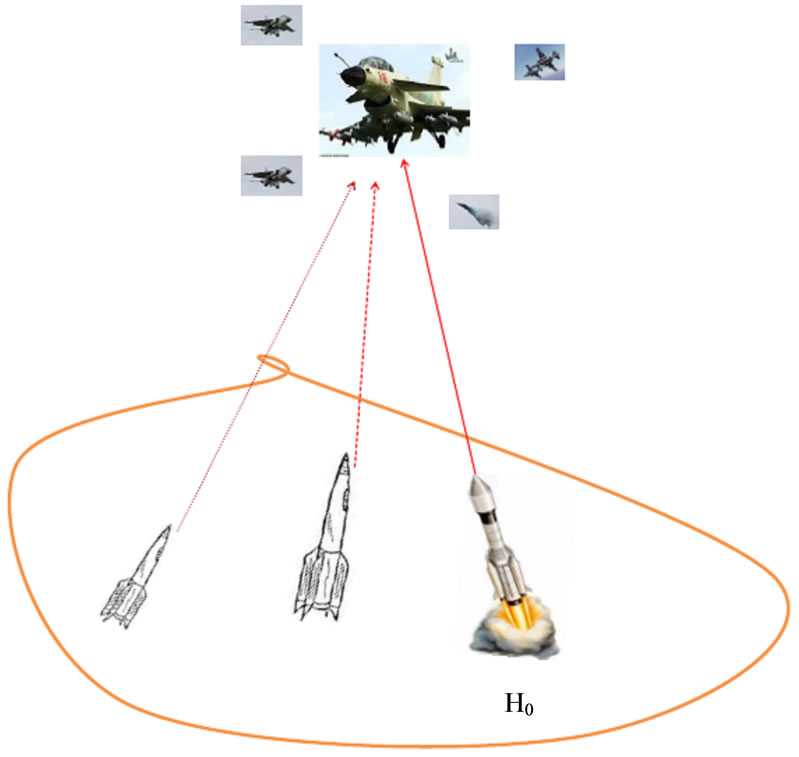
Figure 2. The sheaf of SAM shooting down aircraft noise bomb attack as B52.
(SOPCS) have a high practical significance, as the series of SAM to destroy B52 attack aircraft with fighter jamming, or laser beam to destroy targets, like the beams in materials research of Physical nuclear, etc, … This paper described some types of sheaf optimal problems. We can solve them by Pontryagin’s Principle, Lyapunov’s Energy Function or by the Hamilton’s Principle. In this paper we present the necessary and sufficient conditions for this problem by Hamilton’s Principle, namely by HJB equations.
In the near future, we will set the numerical calculations can be applied to a clearer and will study the different Optimization problems with some controls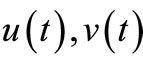 .
.
5. Acknowledgements
The authors gratefully acknowledge the referees for their careful reading and many valuable remarks which improved the presentation of the paper.
REFERENCES
- A. D. Ovsyannikov, “Mathematical methods in sheaf controls,” Leningrad University Pub., Saint Petersburg, 1980.
- N. D. Phu and T. T. Tung, “Some properties of sheafsolutions of sheaf fuzzy control Problems,” Electronic Journal of Differential Equations, Vol. 2006, No. 108, 2006, pp. 1-8.
- N. D. Phu and T. T. Tung, “Some results on sheaf solutions of sheaf set control differential equations,” Journal of Nonlinear Analysis: Theory, Methods & Applications, Vol. 67, No. 5, 2007, pp. 1309-1315. doi:10.1016/j.na.2006.07.018
- N. D. Phu, “On the Global Controllable for Set Control Differential Equations,” International Journal of Evolution Equations, Vol. 4, No. 3, 2009, pp. 281-292.
NOTES
*Corresponding author.

