Advances in Bioscience and Biotechnology
Vol.06 No.02(2015), Article ID:54114,10 pages
10.4236/abb.2015.62012
Large-Scale Kinetic Parameter Identification of Metabolic Network Model of E. coli Using PSO
Mohammed Adam Kunna1, Tuty Asmawaty Abdul Kadir1, Aqeel S. Jaber2, Julius B. Odili1
1Faculty of Computer System and Software Engineering, Universiti Malaysia Pahang, Kuantan, Malaysia
2Faculty of Electrical and Electronic Engineering, Universiti Malaysia Pahang, Kuantan, Malaysia
Email: mohammed87kunna@gmail.com, asmawaty@gmail.com, aqe77el@yahoo.com, odili_julest@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 January 2015; accepted 13 February 2015; published 15 February 2015
ABSTRACT
In metabolic network modelling, the accuracy of kinetic parameters has become more important over the last two decades. Even a small perturbation in kinetic parameters may cause major changes in a model’s response. The focus of this study is to identify the kinetic parameters, using two distinct approaches: firstly, a One-at-a-Time Sensitivity Measure, performed on 185 kinetic parameters, which represent glycolysis, pentose phosphate, TCA cycle, gluconeogenesis, glycoxylate pathways, and acetate formation. Time profiles for sensitivity indices were calculated for each parameter. Seven kinetic parameters were found to be highly affected in the model response; secondly, particle swarm optimization was applied for kinetic parameter identification of a metabolic network model. The simulation results proved the effectiveness of the proposed method.
Keywords:
Metabolic Engineering, Metabolic Network, Dynamic Model, Sensitivity Analysis, Optimization and Estimation

1. Introduction
A major advance in metabolic engineering is possible by understanding the dynamic behavior of a living cell and decreasing or increasing the production of metabolites [1] -[3] . Several key examples demonstrate this. A powerful tool for explaining the properties of the metabolic engineering system can be found in the experiments of the Metabolic Network Model [4] . Kinetic Metabolic Network modelling requires a large number of kinetic parameters. These parameters have been studied and analyzed to detect the concentration of changes in the metabolites and reactions, using a differential algebraic equation [5] . Every physiological system has a set of parameters such as temperature, reaction rates, and kinetic constants. So, to extract the parameters from experimental data in parameter optimization is generally difficult. Hence, the parameters tend to be estimated or measured in different conditions. Therefore, the Least Squares technique and Real-Coded Genetic Algorithm are used to fit the model output to the corresponding experimental measurements applied by [5] . This study focuses on large- scale kinetic parameters, which use a non-linear ODE to estimate kinetic parameters [6] . Since 2002, Sensitivity Analysis and Parameter Optimization have used less than three pathways in their kinetics modeling. In [7] , the model of glycolysis and pentose phosphate pathways was investigated by applying a Stepwise Internalization method for the Sensitivity Analysis, and Simulating Annealing was used to optimize 85 kinetics that represent his model. In [8] , twelve kinetic parameters were identified as effective parameters for the Embden-Meyerhof pathway, pentose phosphate pathway, and phosphortransferase system; they used the Monte Carlo simulation and Sobol method for calculating the times profiles. Nine of the most sensitive kinetic parameters were optimized through the Control Vector Parameterization Approach to formulate Dynamic Parameter Estimation problems [8] . They also apply Sensitivity Analysis to 100 kinetics by scaling each kinetic parameter individually. Seven kinetic parameters were identified as the most significant ones, considering Vmax as a kinetic target. Real- Coded Genetic Algorithm was used for optimization [5] . Particle swarm optimization (PSO) is a relatively new family of algorithms which may be used to find out the optimal solutions to the high complexity or multi- dimensional functions [9] . The algorithm of PSO emulates the behavior of animal societies that don’t have any leader in their group or swarm, such as bird flocking and fish schooling [10] . Moreover, the PSO algorithm contains many different mechanisms that improve global and local exploration abilities [11] . It was also reported that PSO algorithm was sufficient to reduce the steady-state errors [12] .
In this work, the model in [6] is used as a study case. The model consists of glycolysis, pentose phosphate, TCA cycle, gluconeogenesis, glycoxylate pathways, phosphotransferase system and acetate formation. The Sensitivity Analysis in large-scale kinetic parameters was used to select the effective parameters that reveal significant changes among metabolites and fluxes on the model output. On the other hand, PSO was used to optimize the identification of the most effective parameters of the model. The simulation result proved that only seven kinetics were highly affected in the model. Also, it proved that the proposed optimizing method―the PSO algorithm―was highly effective in estimating the unknown parameters.
2. Proposed Method
This paper comprises three parts. The first part presents a brief description of the model structure; the second part shows the application of the local Sensitivity Analysis technique; and the last part covers the application of the Global Optimization Algorithm.
2.1. Metabolic Network of E. coli
The main metabolic pathway of E. coli formulated by reference [6] was treated as a benchmark. This model describes the dynamic metabolic behavior of glycolysis, pentose phosphate, TCA cycle, gluconeogenesis, glycoxylate pathways and acetate formation. It contains 23 metabolites and 28 enzymatic reactions with 10 co- factors (e.g., nad, coa, atp). The corresponding metabolic network is shown in Figure 1 [3] .
The metabolite concentration rate of the changes in this metabolic network is given by the following equation:
 (1)
(1)
where 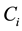 the concentration of metabolite i,
the concentration of metabolite i,  is stoichiometric coefficient of metabolite i in the reaction j,
is stoichiometric coefficient of metabolite i in the reaction j, 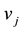 is the rate of the reaction j and
is the rate of the reaction j and 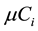 is the growth rate of the dilution effect. All the formulas and the mass balance in this dynamic model are taken from [6] .
is the growth rate of the dilution effect. All the formulas and the mass balance in this dynamic model are taken from [6] .
2.2. Sensitivity Analysis
Large-scale kinetic parameters of experimental data may require to be corrected through the Sensitivity Analysis to identify the parameters which are the most affected in the model output. Sensitivity Analysis is a set of
Figure 1. Metabolic network of E. coli.
analytics and simulation used as a tool to understand the effectiveness of the parameters of the model response [13] . Sensitivity Analysis can be represented by different mathematical perspectives; it gives access to different numerical methods. These methods are divided into local and global methods: local methods consider the small changes in the model inputs, while global methods consider input values as random variables. Moreover, some researchers use different Sensitivity Analysis methods for different tasks. These include Mass and Energy Balance for developing a steady-state kinetic model [14] , and Constraint-Based Analysis to study the impact of genes on the metabolic flux redistribution of S. cerevisiae [15] . In this study we apply the Sensitivity Analysis of large-scale dynamic metabolic networks to E. coli [6] using the method of One-at-a-Time Sensitivity Measures [16] . These will include Standard Deviation to examine the sensitivity changes in the model output, and the coefficient of variation in order to compare Standard Deviation with the original data. This will be done under the continuous culture at the steady state condition, by scaling all the kinetics of 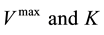 one by one into percentages increasing 10%, 20% and 40%; with dilution rate of 0.1 in these enzymes: pts, pgi, pfk, aldo, gapdh, pyk, pdhpta, acs, ack, cs, icdh, 2 kgdh, sdh, fum, mdh, icl, ms, ppc, pck, mez, g6pdh, 6pgdh, rpe, rpi, tkta, tktb and tal.
one by one into percentages increasing 10%, 20% and 40%; with dilution rate of 0.1 in these enzymes: pts, pgi, pfk, aldo, gapdh, pyk, pdhpta, acs, ack, cs, icdh, 2 kgdh, sdh, fum, mdh, icl, ms, ppc, pck, mez, g6pdh, 6pgdh, rpe, rpi, tkta, tktb and tal.
3. Parameters Identification
Normally, estimation of the unknown parameters techniques is based on the difference between the simulated model and behavior in the actual system model [13] . The function, that used to identify the large-scale metabolic network of E. coli system model, and the transfer, is as follows:
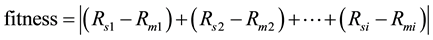 (2)
(2)
where, 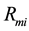 has the model reaction rate resulted for
has the model reaction rate resulted for  kinetics and
kinetics and  is the simulation reaction rate result for
is the simulation reaction rate result for  kinetics.
kinetics.
In order to identify the kinetic parameters sensitivity of the model employed by [6] we apply the PSO algorithm to the seven kinetics to fit both the simulation (Sensitivity Analysis) and the real values of the model [6] by using experimental metabolites data taken from [17] . The concentration of metabolites used in the optimization execution needs to fit the result of our metabolites simulation model closely. To achieve this the concentration is as follows: fructose 1,6-bisphosphate (0.67 mM), phosphoenol-pyruvate (1.04 mM), isocitrate (0.21 mM), 2-keto-D-gluconate (0.134 mM). PSO was introduced by Eberhart and Kennedy as a new heuristic method [18] . During the PSO execution, the maximum number of generations is set as 100 (bird-steps); the dimension’s problem is 7 kinetic parameters; the population size (iterations) repeats 100 times; linear inertia weight is 0.9; PSO parameter C1 = 1.5 and C2 = 0.8, with lower and upper values for each kinetics. PSO was inspired by the food-searching behaviors of fish and their activities or a flock of birds in D-dimensional search space. The best individual position of particle i and the best position of the entire swarm are represented by [18] :
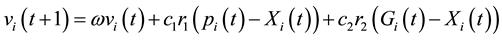 (3)
(3)
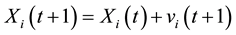 (4)
(4)
where Pi is the best position already found by particle i until time t and G is the best position already found by a neighbor until t, 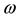 is an inertia weight parameter to exploration search space. c1, c2 are acceleration coefficients toward P and G respectively, and r1, r2 are random number between 0 and 1. In each iteration, the particles will use Equations (3) and (4) to update their position
is an inertia weight parameter to exploration search space. c1, c2 are acceleration coefficients toward P and G respectively, and r1, r2 are random number between 0 and 1. In each iteration, the particles will use Equations (3) and (4) to update their position  and velocity
and velocity
Figure 2. PSO algorithms.
4. Result
4.1. Sensitivity Analysis
The One-at-a-Time Sensitivity Measures identify 7 kinetic parameters from 185 kinetic parameters of [6] . They are V_PYKmax, n_PK, ICDH, Kf_ICDH, Kd_ICDHnadp, Km_ICDHnadp and V_ICLmax. These represent the reaction rate of








The changes in the V_PYKmax result show that the metabolites of FDP and ICIT are highly increased, while ACE is highly decreased. The increase in the enzyme of ALDO is due to the decrease in GLcex, which in turn is regulated by its effectors ATP, ADP and PEP (as described in Figure 3 and Figure 4). The changes in n_PK show that the metabolites of FDP, GAPDHAP, PEP, ICIT and E4P are highly increased; ACP, ACE and S7P are highly decreased. The enzyme of Aldo is highly increased and Pta, Ack and Pck are highly decreased due to a significant reduction in GLCex. This in turn is regulated by the same V_PYKmax effectors described decreasing in GLCex, which is then in turn regulated by those same V_PYKmax effectors described in Figure 5 and Figure 6. The changes in results for ICDH, Kf_ICDH and Kd_ICDHnadp show that highly increasing levels of the meta- bolite of ICIT and deviation in the Km_ICDHnadp result have the effect of greatly reducing ICIT also. This is then in turn regulated by its effectors NADP, NADPH and 2KG, as shown in Figures 7-14 respectively. The changes in V_ICLmax will be shown in Figure 15 and Figure 16. Moreover the kinetics of ICDH and Kf_ICDH have the same results, and these may be to ascribed to increasing levels of ICIT metabolites.
Figure 3. The effect of V_PYKmax in metabolites.
Figure 4. The effect of V_PYKmax in enzymes.
Figure 5. The effect of n_PK in metabolites.
Figure 6. The effect of n_PK in enzymes.
Figure 7. The effect of ICDH kinetic in metabolites.
Figure 8. The effect of ICDH kinetic in enzymes.
Figure 9. The effect of Kf_ICDH kinetic in metabolites.
Figure 10. The effect of Kf_ICDH kinetic in enzymes.
Figure 11. The effect of Kd_ICDHnadp kinetic in metabolites.
4.2. Optimization
All the kinetic parameters executed on the particle swarm optimization algorithm, whose lower and upper values are started by ±1 in order to reach the best lower and upper boundaries, achieved the best optimum values. The optimized parameters are tested in the same model to reduce the errors between the experimental data and actual model data. This will be the focus of the next section. The optimal values are shown in Table 1.
Figure 12. The effect of Kd_ICDHnadp kinetic in enzymes.
Figure 13. The effect of Km_ICDHnadp kinetic in metabolites.
Figure 14. The effect of Km_ICDHnadp kinetic in enzymes.
Figure 15. The effect of V_ICLmax kineticin metabolites.
Figure 16. The effect of V_ICLmax kineticin enzymes.
4.3. Validation
In oreder to prove that, the one-at-a-time sensitivity analysis measure and PSO algorithm methods has great impact in optimizing large-scale kinetic parameters, the original kinetic parameters in the model formulated by Kadir [6] which are V_PYKmax, n_PK, ICDH, Kf_ICDH, Kd_ICDHnadp, Km_ICDHnadp and V_ICLmax are replaced by the opimum kinetic parametrs values in Section 4.2 then tested. The validation results shown in Figure 17 there are 4 metabolites moved closely to the experimental data which these metabolites are FDP, PEP, ICIT and 2KG.
Figure 17. The metabolites estimation.
Table 1. Kinetics optimization.
5. Conclusion
This study has applied One-at-a-Time Sensitivity Measures to assess the effectiveness of large-scale kinetic parameters in a dynamic metabolic network into the steady-state condition of E. coli. By programming to measure how much they affect the model response, the analysis has identified seven particular kinetic parameters as being the most effective in their allowable range. Particle swarm optimization algorithm has been applied to the kinetics result of the sensitivity analysis, based on continuous culture with a dilution rate of 0.1 to fit our result in the model output of [6] . Further investigations, particularly the inclusion of Kinetic Parameter Optimization, are needed to give a precise result regarding the relation between the Sensitivity Analysis methods and the system dynamic properties. Finally, the validation of numerical results shows that the large-scale kinetic parameters optimization procedure has provided effective estimation.
Acknowledgements
The authors gratefully acknowledge financial support from the Universiti Malaysia Pahang, Faculty of computer system and software engineering. The authors thank Dr. Tuty Asmawaty Abdul Kadir, who provided the model under study and Dr. Md. Aminul Hoquea for providing the experimental data set.
Cite this paper
MohammedAdam Kunna,Tuty AsmawatyAbdul Kadir,Aqeel S.Jaber,Julius B.Odili, (2015) Large-Scale Kinetic Parameter Identification of Metabolic Network Model of E. coli Using PSO. Advances in Bioscience and Biotechnology,06,120-130. doi: 10.4236/abb.2015.62012
References
- 1. Berry, A., Dodge, T.C., Pepsin, M. and Weyler, W. (2002) Application of Metabolic Engineering to Improve Both the Production and Use of Biotech Indigo.
Journal of Industrial Microbiology & Biotechnology, 28, 127-133.
http://download.springer.com/static/pdf/328/art%253A10.1038%252Fsj%252Fjim%252F7000228.pdf?auth66=1408430581_f695792c4483a692fced6688ab3304cd&ext=.pdf
http://dx.doi.org/10.1038/sj.jim.7000228 - 2. Wright, B.E., Butler, M.H. and Albe, K.R. (1992) Systems Analysis of the Tricarboxylic Acid Cycle in Dictyostelium discoideum. Journal of Biological Chemistry, 267, 3101-3105.
http://www.jbc.org/content/267/5/3106.full.pdf - 3. Nikolaev, E.V. (2010) The Elucidation of Metabolic Pathways and Their Improvements Using Stable Optimization of Large-Scale Kinetic Models of Cellular Systems.
Elsevier Journal Metabolic Engineering, 12, 26-38.
http://ac.els-cdn.com/S1096717609000718/1-s2.0-S1096717609000718-main.pdf?_tid=661cb9a0-25d6-11e4-bb74-00000aacb362&acdnat=1408256529_6ae343443dc3684966093f1fcdecbc33
http://dx.doi.org/10.1016/j.ymben.2009.08.010 - 4. Copeland, W.B., Bartley, B.A., Chandran, D., Galdzicki, M., Kim, K.H., Sleight, S.C., Maranas, C.D. and Sauro, H.M. (2012) Computational Tools for
Metabolic Engineering. Metabolic Engineering, 14, 270-280.
http://www.sciencedirect.com/science/article/pii/S1096717612000250
http://dx.doi.org/10.1016/j.ymben.2012.03.001 - 5.
Tohsato, Y., Ikuta, K., Shionoya, A., Mazaki, Y. and Ito, M. (2013) Parameter Optimization and
Sensitivity Analysis for Large Kinetic Models Using a Real-Coded Genetic Algorithm. Gene, 518, 84-90.
http://ac.els-cdn.com/S0378111912015508/1-s2.0-S0378111912015508-main.pdf?_tid=f1cc98fe-25d5-11e4-b24d-00000aacb361&acdnat=1408256334_5e4e17ed6dec6011fcfe6327b7176952
http://dx.doi.org/10.1016/j.gene.2012.11.080 - 6.
Kadir, T.A.A., Mannan, A.A., Kierzek, A.M., McFadden, J. and Shimizu, K. (2010) Modeling and Simulation of
the Main Metabolism in Escherichia coli and Its Several Single-Gene Knockout Mutants with Experimental
Verification. Microbial Cell Factories, 9, 88.
http://www.readcube.com/articles/10.1186/1475-2859-9-88
http://dx.doi.org/10.1186/1475-2859-9-88 - 7.
Chassagnole, C., Noisommit-Rizzi, N., Schmid, J.W., Mauch, K. and Reuss, M. (2002) Dynamic Modelling of the
Central Carbon Metabolism of Escherichia coli. Biotechnology and Bioengineering, 79, 53-73.
file:///C:/Users/fskkp/Downloads/0046352641930e5577000000%20(2).pdf
http://dx.doi.org/10.1002/bit.10288 - 8. Di Maggio, J., Ricci, J.C.D. and Diaz, M.S. (2010) Parameter Estimation in Kinetic Models for Large Scale Metabolic Networks with Advanced Mathematical Programming Techniques. Computer Aided Chemical Engineering, 28, 355-360.
http://www.aidic.it/escape20/webpapers/358DiMaggio.pdf - 9. Abido, M.A. (2009) Multiobjective Particle Swarm Optimization for Environmental/Economic Dispatch Problem.
Electric Power Systems Research, 79, 1105-1113.
http://www.sciencedirect.com/science/article/pii/S0378779609000388
http://dx.doi.org/10.1016/j.epsr.2009.02.005 - 10. Jaber, A., Ahmad, A. and Abdalla, A. (2013) An Investigation of Scaled-FLC Using PSO for Multi-Area Power System Load Frequency Control. Energy and Power
Engineering, 5, 458-462.
http://www.scirp.org/journal/PaperInformation.aspx?paperID=38367#.VAFricWSyME
http://dx.doi.org/10.4236/epe.2013.54B088 - 11. Rini, D.P., Shamsuddin, S.M. and Yuhaniz, S.S. (2011) Particle Swarm Optimization (PSO) Based Turbine Control. International Journal of Computer Applications, 14, 19-27.
http://www.ijcaonline.com/volume14/number1/pxc3872331.pdf - 12. Baker, S.M., Schallau, K. and Junker, B.H. (2010) Comparison of Different Algorithms for Simultaneous Estimation of Multiple Parameters in Kinetic Metabolic Models. Journal of Integrative Bioinformatics, 7, 133.
http://journal.imbio.de/articles/pdf/jib-133.pdf - 13. Mauch, K., Arnold, S. and Reuss, M. (1997) Dynamic Sensitivity Analysis for Metabolic Systems. Chemical Engineering Science, 52, 2589-2598.
http://ac.els-cdn.com/S0009250997000754/1-s2.0-S0009250997000754-main.pdf?_tid=2768a03e-25d6-11e4-9516-00000aacb35f&acdnat=1408256424_6a3d35b3403561719dbedd588c0cca68 - 14. Dasila, P.K., Choudhury, I., Saraf, D., Chopra, S. and Dalai, A. (2012) Parametric Sensitivity Studies in a Commercial FCC Unit. Advance in Chemical Engineering and Science, 2, 136-149.
http://dx.doi.org/10.4236/aces.2012.21017 - 15. Xu, Z.-X. and Sun, X. (2008) Constrain-Based Analysis of Gene Deletion on the Metabolic Flux Redistribution of Saccharomyces cerevisiae. Journal of Biomedical Science and Engineering, 1, 121-126.
http://www.srpublishing.org/journal/jbise - 16. Campolongo, F., Cariboni, J. and Saltelli, A. (2007) An Effective Screening Design for Sensitivity Analysis of Large Model. Environmental Modelling & Software, 22, 1509-1518.
http://www.stat.osu.edu/~comp_exp/jour.club/CamCarSal_EngModellingSoftware-2007.pdf - 17. Hoquea, M.A., Ushiyamab, H., Tomitaa, M. and Shimizua, K. (2005) Dynamic Responses of the Intracellular Metabolite Concentrations of the Wild Type and pykA Mutant Escherichia coli against Pulse Addition of Glucose or NH3 under Those Limiting Continuous Cultures. Biochemical Engineering
Journal, 26, 38-49.
http://www.sciencedirect.com/science/article/pii/S1369703X05001865
http://dx.doi.org/10.1016/j.bej.2005.05.012 - 18. Eberhart, R.C. and Kennedy, J. (1995) A New Optimizer Using Particle Swarm Theory. Proceedings of the 6th International Symposium on Micro Machine and Human
Science, Nagoya, 4-6 October 1995, 39-43.
http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=494215
http://dx.doi.org/10.1109/MHS.1995.494215
Nomenclatures
Metabolites
Glcex: Glucose;
G6P: Glucose-6-phosphate;
F6P: Fructose-6-phosphate;
FDP: Fructose 1,6-bisphosphate;
GAP: Glyceraldehyde 3-phosphate;
DHAP: Dihydroxyacetone phosphate;
PEP: Phosphoenolpyruvate,
PYR: Pyruvate;
AcCOA: Acetyl-CoA;
AcP: Acetyl phosphate;
ACE: Acetate;
ICIT: Isocitrate;
2KG: 2-Keto-D-gluconate;
SUC: Succinate;
FUM: Fumarate;
MAL: Malate;
OAA: Oxaloacetate;
6PG: 6-Phosphogluconolactone;
Ru5P: Ribose 5-phosphate;
Xu5P: Xylulose 5-phosphate;
R5P: Ribulose 5-phosphate;
S7P: Sedoheptulose 7-phosphate;
E4P: Erythrose 4-phosphate.
Enzymes
PTS: Phosphotransferase system;
PGI: Phosphoglucose isomerase/glucosephosphate isomerase;
PFK: Phosphofructokinase-1;
ALDO: Aldolase;
GAPDH: Glyceraldehyde 3-phosphate dehydrogenase;
Pyk: Pyruvate kinase;
PDH: Pyruvate dehydrogenase;
Acs: Acetyl coenzyme A synthetase;
Pta: Phosphotransacetylase;
Ack: Acetate kinase;
CS: Citrate synthase;
ICDH: Isocitrate dehydrogenase;
2KGDH: 2-Keto-D-gluconate dehydrogenase;
SDH: Succinate dehydrogenase;
Fum: Fumarase;
MDH: Malate dehydrogenase;
Mez: Malic enzyme;
Pck: Phosphoenolpyruvate carboxykinase;
Ppc: PEP carboxylase;
ICL: Isocitratelyase;
Ms: Malate synthase;
G6PDH: Glucose-6-phosphate dehydrogenase;
6PGDH: 6-Phsophogluconate dehydrogenase;
Rpi: Ribulose 5-phosphate 3-isomerase;
Rpe: Ribulose phosphate 3-epimerase;
Tkta: Transketolase I;
Tktb: Transketolase II;
Tal: Transaldolase.



















