Modern Economy
Vol.06 No.12(2015), Article ID:62083,8 pages
10.4236/me.2015.612118
A Pure Capital Market Complementarity between Immigrants and Natives
Adolfo Cristóbal Campoamor
Department of Economics, Loyola University in Andalusia, Sevilla, Spain

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 November 2015; accepted 16 December 2015; published 21 December 2015
ABSTRACT
This work presents a model aiming to evaluate the impact of rural-urban migration on the aggregate stock of loanable funds and investment by the urban population. Much higher investment costs for immigrants in cities prevent their acquisition of either human or physical capital. That is the reason why immigrants self-select as net lenders and affect urban labor earnings by means of the availability of new loanable funds for investment. This reduces the local interest rates and facilitates urban aggregate investment, especially by the new generations of natives. As a result of that, the aggregate labor income of natives increases unambiguously with the size of new immigration waves.
Keywords:
Rural-Urban Migration, Investment Costs, Loanable Funds

1. Introduction
According to abundant analyses about many less developed countries, rural-urban migration often results in a socioeconomic marginalization of new immigrants in the urban life. Despite the effort often allowing them to become upward movers in response to substantial opportunities for economic betterment, they usually exhibit relatively lower probabilities of economic success. In this sense, a lower economic mobility of rural-urban migrants is both a cause and a consequence of segregated labor markets. In such markets, those immigrants with lower entrepreneurship capacity and human capital are unlikely to associate with highly qualified natives.
Such segregation is also limiting the competition between migrants and the native urbanites with the lowest qualification. More specifically, some recent empirical results uncover an insignificant, and often slightly positive, impact of higher migratory flows on the income and employment of unqualified, native urbanites. This is a standard empirical result, emerging in the context of many different countries, although it is at odds with most of the theoretical predictions. Therefore, “the inconsistency between the theory and the empirical evidences has shaken the basis of the traditional belief that an immigrant influx should lower the wage of competing factors […] and calls for new evidence and new explanations” [1] .
In this respect, our model offers a potential explanation based on a pure capital market complementarity between immigrants and natives. Given that the former turn out to become new, relevant net lenders in the city, it is now easier for the new generations of urbanites to undertake an investment in human capital or an acquisition of entrepreneurial capacity. Our choice of the Chinese case as a plausible illustration for the model is due to “an intriguing empirical confluence” [2] : the massive urbanization has been paralleled by a spectacular rise in the urban, domestic saving rates from the beginning of the current century in China. The resilience of Chinese institutions that tend to marginalize rural-urban migrants, together with the recent urbanization, may have been crucial to understand the recent Chinese accumulation and inequality patterns.
To summarize, our Chinese image is useful to illustrate a novel theoretical hypothesis, related to an immigration surplus enlarged by a complementarity in the capital markets. Such hypothesis is clearly different from the traditional complementarity in the labor markets, whose empirical implications were explored and popularized by Borjas [3] [4] . In Section 2 we will develop our model. Section 3 will connect it with other related theoretical work in the literature. Section 4 will try to link the theoretical findings to some features of the Chinese institutional reality. The conclusion is in Section 5.
2. The Model
Our urban economy consists of a population of natives (also called urbanites) whose size is normalized to one. In period t there exists an unexpected migratory shock by which M rural migrants arrive to the city. They will start their urban life during the youth, before undertaking any form of investment. A crucial driving force in our chain of causality is the immigrants’ investment costs being higher than those of natives. Despite this fact, the investment possibilities offered by the urban credit markets are supposed to be absent in their original rural environment. In this sense, we are adopting Lucas’s (2004) [5] vision in his theoretical analysis of rural-urban migration: cities are understood as ideal environments for the acquisition of human capital and entrepreneurial knowledge.
2.1. Technology
Our urban economy exhibits a technology combining skilled and unskilled labor to produce a single good. Both labor and product markets are perfectly competitive. It is noticeable that most of the models dealing with an immigration surplus are based on labor market complementarities between unskilled labor and physical capital and/or skilled labor. In these models, the reduction in the remuneration of unskilled labor gives rise to a net gain for the native population, since the capital owners and skilled workers will appropriate a new surplus. Those productive factors will gain, whereas the unskilled workers will be damaged. As Borjas [3] noted, in that context “the economic benefits from immigration arise only when immigrants do lower the wage of native workers”.
In contrast to these explanations, here we will focus on a pure capital market complementarity. In order to sharpen our theoretical point, skilled and unskilled labor will be perfect substitutes and hence their respective salaries will not be affected by immigration. We will then show how the availability of new loanable funds for investment, and the consequent reduction of the equilibrium interest rate, will facilitate the skill upgrading of the new generations. This will give rise to an increase in the aggregate labor income of natives. Our assumption of perfect substitutability is convenient to eliminate any sort of labor market complementarity and emphasize our chain of causality. The value of the unskilled urban wage is equal to one and the skilled wage will be given by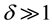 .
.
2.2. Preferences
The timing of our model is based on Galor and Zeira [6] . Every individual, who represents a generation within every dynasty, lives for two periods. In the first period he must decide whether to invest or not; the precise form of his investment (e.g. in human capital; in the creation of a startup, etc) will not be determinant to us. Only in the case he decides to invest will a parental bequest be available to him, reducing his investment costs. In the second period he will work according to his previous decision, consume and have a child, to whom he could potentially leave a bequest.
In the second period of his life, the parent observes his child’s ability. In case he finds the child capable enough, he will facilitate his investment during that particular period. The amount of the bequest will depend on the specific form of the parent’s altruistic preferences. In particular, in this case we will assume the parent derives utility from the child’s gross income, computed at the time the child will consume after his parent’s death. This is a form of income-based altruism à la Becker and Tomes [7] . Let us consider the following linear utility function:
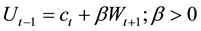 (1)
(1)
This function represents the utility level of an individual born at (t − 1), where ct stands for his own consumption in the second period of his life. Wt+1 represents the gross income obtained by the following generation, born at period t, which will be used by that child to consume and/or leave another potential bequest at period (t + 1). Finally, β is an indicator of the level of parental altruism towards the next generation.
2.3. Decisions to Invest and to Bequeath
If a young person born at t decides to invest in that period, he will have to ask immediately for a loan to cover his investment costs. Without loss of generality, let us consider the case of a human capital investment in which the native (immigrant) investor must hire a certain number
 (
(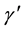 ) of qualified instructors. Let us also assume that
) of qualified instructors. Let us also assume that . The young investor will have to return the principal and the interests in period (t + 1), once he has received a remuneration in the labor market. His own intrinsic ability (a), combined with the parental bequest (x), will allow him to reduce his final investment cost.
. The young investor will have to return the principal and the interests in period (t + 1), once he has received a remuneration in the labor market. His own intrinsic ability (a), combined with the parental bequest (x), will allow him to reduce his final investment cost.
2.3.1. Decision by the Child
When an individual born at t decides whether he should invest or not, he makes the following comparison:
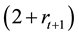 will be his earnings derived from an unqualified profession, whereas
will be his earnings derived from an unqualified profession, whereas
 will be the earnings emanating from a qualified job. The term
will be the earnings emanating from a qualified job. The term
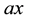 stands for the amount of instruction he can skip due to the familial bequest and his idiosyncratic ability. All these earnings are measured in monetary units of period (t + 1), given that it is then when his consumption will take place.
stands for the amount of instruction he can skip due to the familial bequest and his idiosyncratic ability. All these earnings are measured in monetary units of period (t + 1), given that it is then when his consumption will take place.
Those individuals who decide to remain unskilled will work in both periods of their life and will save their initial earnings until period (t + 1), when they will be able to both consume and leave a legacy. On the other hand, the individuals born at t willing to become skilled will borrow to cover their investment costs at t; and will repay their debt at (t + 1), once they have received their wage. Therefore, we can compare both expressions above and solve for the lowest ability level necessary to qualify. A native individual born at t will choose to invest if
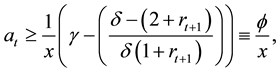 where
where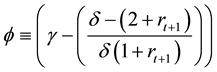 (2)
(2)
We will find a similar expression for a young immigrant, just by replacing
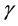 by
by . This higher investment cost borne by young immigrants reflects their frequent institutional marginalization in the urban society.
. This higher investment cost borne by young immigrants reflects their frequent institutional marginalization in the urban society.
2.3.2. Decision by the Parent
Let us assume that every parent observes the realization of the random variable corresponding to his child’s ability. Then he will decide to leave a bequest or not on the basis of such realization. Given that our form of parental altruism assigns utility to the gross future income of the child, the parent will only bequeath the amount being strictly necessary for his child’s investment. This implies that, only if the child is skillful enough to re-
ceive a bequest, according to our expression (2) such legacy will be exactly equal to , with
, with
 being the child’s ability shock realization. Therefore, it will be convenient for the parent to bequeath only if
being the child’s ability shock realization. Therefore, it will be convenient for the parent to bequeath only if
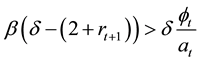 (3)
(3)
The left-hand side of the inequality captures the parental altruistic benefit from the extra income accruing to a child that invests. The right-hand side reflects the cost of the bequest for the parent. Therefore, taking into account (2) and (3), the parent will decide to bequeath if
 (4)
(4)
This cutoff value

biguously,
discourage more people from investing and will increase the necessary ability cutoff required to receive a bequest.
Let us denote now by






2.4. Existence and Uniqueness of a Competitive Equilibrium
In our economy, a competitive equilibrium is characterized by an interest rate and an allocation of native and immigrant workers to the skilled and unskilled occupations, such that the supply of credit is identical in every period to the demand for credit. Such credit will be entirely used by the next generation of qualified workers to invest when young. In other words, we must look for a sequence of equilibrium interest rates that clear the credit market in every particular time period.
In our credit market we can observe two distinct sources of saving at any period t: the young generations who choose not to invest and save their whole unskilled wage to face their adulthood at (t + 1); the adults born at (t − 1) with sufficiently skillful children, who will save at t in order to leave a bequest, according to our Section 2.3.2. On the other hand, the demand for credit to invest comes from the most capable youngsters among the population of natives and immigrants. These young people’s individual demand for credit will be equal to the remuneration of qualified instructors they need to hire at t; that is,



On the left-hand side of the last equation we have the supply of loanable funds by the unskilled young people. On the right-hand side we can observe the aggregate expenditure on investment, equivalent to the remuneration of qualified instructors minus the cost skipped due to the parental bequests. Considering the expressions (2) and (5), the last equation could be simplified as follows:

It is important to notice that, since Equations (5) and (6) depend on the interest rate of a single period (t + 1), our equilibrium interest rate will be always identical. This fact makes our analysis finally static, which facilitates its resolution and interpretation. By rearranging our Equation (6), it is possible to obtain a lemma that specifies sufficient conditions for the existence and uniqueness of the competitive equilibrium.
Lemma: If

The proof of this lemma is examined in the final Appendix. The uniqueness of the competitive equilibrium is ensured by an excess demand function that is strictly decreasing in the credit market. It is crucial to have profitable enough investment opportunities: they will guarantee the existence of an active “demand side” in the market for credit. Those opportunities must be advantageous both from the point of view of the investment benefits (


2.5. The Availability of Additional Loanable Funds
Now we are ready to derive our main effect of immigration on the availability of loanable funds for investment. As we anticipated above, in this setting the supply of credit comes from the unskilled workers. The most capable youngsters will receive such credit to finance the share of investment costs that is not covered by their parents’ bequests. Consequently, a new immigration wave brings about a higher proportion of unskilled workers providing net lending, due to their very high investment costs. This will be useful to reduce the equilibrium interest rate (
Therefore, for a new migratory influx to provide a higher volume of loanable funds, it is necessary that immigrants face higher investment costs (
Proposition. A higher migratory shock (that is, a rise in the value of M) will reduce


Proof. We can differentiate both sides of Equation (6) with respect to M, computing the total derivative, and obtain

where


If we now insert (8) inside (7), we can finally conclude that

We can check from expression (4) that
tive for sure. Because of that, for (9) to yield a negative value we will clearly need a numerator that is lower than zero, which requires that
Given that the cutoff ability values are increasing in



Finally, we know that in our model all wages are invariant and
3. Connections with Related Theoretical Literature
Some recent theoretical models, often inspired by the Chinese reality, have considered the possibly beneficial effects of inter-regional migration restrictions from the viewpoint of capital accumulation and/or allocative efficiency. Among them we will mention Fan and Stark [8] and Vendryes [9] . Fan and Stark [8] present a static model where human capital externalities in cities cause the possible inefficiency of free migration. The agglomeration in Eastern China would deprive the Western region of an important stock of human capital. Simultaneously, its huge abundance in the East would finally depreciate its stock value, despite the positive externalities.
On the other hand, Vendryes [9] also concludes, in a dynamic model of capital accumulation, that a perfect East-West integration of capital and labor markets would give rise to a huge agglomeration in China. This would attract such a volume of capital to the East that even the Western interest rate would fall, wages would rise and there would be lower aggregate savings and growth at the national level. Unlike these two articles, our paper proposes that a higher rural-urban migration may be beneficial, as long as there are certain institutional hurdles for the investment of immigrants in cities. In other words, we emphasize the role played by a more intense rural- urban migration in the presence of sufficiently high investment costs for immigrants.
4. Chinese Cities as a Potential Illustration
The system of geographical registration for Chinese families (hukou) imposes strong restrictions for rural immigrants to access the main urban public services (healthcare, education, pensions, etc.). In the context of our model, this institution establishes higher investment costs in human capital or entrepreneurial activities to the newcomers with rural hukou, limiting their economic mobility in cities. In particular, Heckman [10] estimates that the extra cost of education for immigrants’ children amounts to 10% of family income in Chinese cities. In fact, according to the 2010 census there are about 260 million people working and living in a location other than the one they are registered at. A significant proportion of the students with a rural hukou must start their education at informal schools, managed by the immigrants themselves.
Such a highly discriminatory character of the Chinese institutions against the floating population is making immigrants exhibit higher net saving rates, in order to cover their future expenses on healthcare, retirement or bequests. Therefore, they are less likely than natives to undertake human capital or entrepreneurial investments. According to Huang’s survey (2010) [2] , “in 2007, the saving rate of the households with urban hukou in Guangzhou was 15.6%; in Shenzhen it was 27.5%. In contrast, the immigrant workers with rural origin showed in 2007 a saving rate per household of 41%, whereas those in Shenzhen showed one of 42%”. These extra net savings may well have boosted the Chinese capital accumulation.
To summarize, we claim that the resilience of the hukou institution, in parallel with the massive recent urbanization, is probably important to understand some recent patterns of accumulation and inequality in China. That Asian image is useful as an illustration for our novel theoretical hypothesis: capital market complementarities, and not only labor market complementarities, may enlarge the immigration surplus as well.
5. Conclusions
In this work we have presented a novel theoretical mechanism giving rise to an immigration surplus, even in the absence of variations in skilled or unskilled labor remunerations. Immigrants, who are eager to save in the city to guarantee a decent status in old age, or a decent bequest to their children, find it especially difficult to undertake any form of real capital investment. Because of that, there will be a considerable abundance of extra loanable funds in the urban financial system. And it will be the native population who will mostly take advantage of such situation to borrow at lower interest rates given their lower investment costs in human or entrepreneurial capital.
Studying the case of China has been useful as a potential illustration. In 1978 only 18% of the Chinese population used to live in cities. However, by 2003 both the number and the size of its cities had grown so much that the urbanization rate was 41% [11] . Simultaneously, from the beginning of the new century the share of national consumption over GDP experienced a huge fall, to the extent that the domestic saving rate reached an amazing 52% in 2006. Here we suggest that the confluence of the hukou regime with a massive rural-urban migration, in the midst of a climate of economic insecurity, may have contributed to a really fast pace of capital accumulation.
Acknowledgements
I would like to express my gratitude to Juan Dolado, Michael Manove and especially Dilip Mookherjee for their stimulus and very useful comments. The usual disclaimer applies.
Cite this paper
Adolfo CristóbalCampoamor, (2015) A Pure Capital Market Complementarity between Immigrants and Natives. Modern Economy,06,1253-1260. doi: 10.4236/me.2015.612118
References
- 1. Meng, X. and Zhang, D.D. (2010) Labor Market Impact of Large Scale Internal Migration on Chinese Urban “Native” Workers. Discussion Paper No. 5288, IZA, Bonn.
- 2. Huang, Y. (2010) Urbanization, Hukou System and Government Land Ownership: Effects on Rural Migrant Workers and on Rural and Urban Hukou Residents. Background Paper for the Global Development Outlook 2010, Shifting Wealth: Implications for Development. OECD Development Centre, Paris.
- 3. Borjas, G.J. (1995) The Economic Benefits from Immigration. The Journal of Economic Perspectives, 9, 3-22. http://dx.doi.org/10.1257/jep.9.2.3
- 4. Borjas, G.J. (2003) The Labor Demand Curve Is Downward Sloping: Reexamining the Impact of Immigration on the Labor Market. Quarterly Journal of Economics, 118, 1335-1374. http://dx.doi.org/10.1162/003355303322552810
- 5. Lucas, R. (2004) Life Earnings and Rural Urban Migration. Journal of Political Economy, 112, 2.
- 6. Galor, O. and Zeira, J. (1993) Income Distribution and Macroeconomics. Review of Economic Studies, 60, 35-52. http://dx.doi.org/10.2307/2297811
- 7. Becker, G. and Tomes, N. (1979) An Equilibrium Theory of the Distribution of Income and Intergenerational Mobility. Journal of Political Economy, 87, 1153-1189. http://dx.doi.org/10.1086/260831
- 8. Fan, C.S. and Stark, O. (2008) Rural-to-Urban Migration, Human Capital and Agglomeration. Journal of Economic Behavior & Organization, 68, 234-247. http://dx.doi.org/10.1016/j.jebo.2008.04.003
- 9. Vendryes, T. (2011) Migration Constraints and Development: Hukou and Capital Accumulation in China. China Economic Review, 22, 669-692. http://dx.doi.org/10.1016/j.chieco.2011.08.006
- 10. Heckman, J. (2005) China’s Human Capital Investment. China Economic Review, 16, 50-70. http://dx.doi.org/10.1016/j.chieco.2004.06.012
- 11. Naughton, B. (2007) The Chinese Economy: Transitions and Growth. MIT Press, Cambridge.
Appendix: Proof of the Lemma
We are now ready to prove the existence and uniqueness of a competitive equilibrium in our model. Let us denote by r* our candidate for an equilibrium interest rate. If we multiply both sides of expression (6) by (1 + r) and rearrange, it is possible to characterize in a different way the credit market equilibrium. Let us first define the function Z(r) as follows:

From the Equation (6) it is possible to observe that our equilibrium interest rate must satisfy the condition


That means that


That holds because, for

It is relatively straightforward to show that



there exists a unique value for r* such that



If, additionally,




and the equilibrium is unique.
Moreover, we also know that



