Modern Economy
Vol.06 No.06(2015), Article ID:57255,9 pages
10.4236/me.2015.66067
In-Arrears Interest Rate Derivatives under the 3/2 Model
Joanna Goard
School of Mathematics and Applied Statistics, University of Wollongong, Wollongong, Australia
Email: joanna@uow.edu.au
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 May 2015; accepted 15 June 2015; published 18 June 2015
ABSTRACT
Lie symmetry methods are used to find a closed form solution for in-arrears swaps under the 3/2 model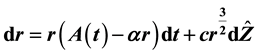 . As well, approximate solutions are found for short-tenor in- arrears caplets and floorlets under the same interest rate model. Comparisons are made of the approximate option values with those obtained with a computationally-intensive numerical scheme. The approximate pricing is found to be substantially fast and easy to implement, while the relative errors with respect to the “true” prices are very small.
. As well, approximate solutions are found for short-tenor in- arrears caplets and floorlets under the same interest rate model. Comparisons are made of the approximate option values with those obtained with a computationally-intensive numerical scheme. The approximate pricing is found to be substantially fast and easy to implement, while the relative errors with respect to the “true” prices are very small.
Keywords:
In-Arrears Swaps, Interest Rate Options, 3/2 Model

1. Introduction
Interest rate derivatives are contracts whose value depends in some way on the level of interest rates. Swap contracts have existed since the early 1980s and since then there has been significant growth in terms of volume and diversity of contracts. In general an interest rate swap is an agreement between two companies, whereupon one company agrees to pay cash flows equal to the interest on a predetermined fixed rate on a notional principal, X, at regular set times  (e.g. every 6 months) over the length of the contract time and in return receives interest at a floating rate (usually the LIBOR rate) on the same notional amount on the same set payment periods within the contract time. In the “plain vanilla” interest rate swap, the floating rate is the rate that prevails at the previous payment date, or in the case of the first payment, the rate at the opening of the contract. With LIBOR- in-arrears swaps, the floating rate paid on a payment date equals the rate observed on the payment date itself. Hence the floating leg cannot be valued as the sum of forward LIBORs.
(e.g. every 6 months) over the length of the contract time and in return receives interest at a floating rate (usually the LIBOR rate) on the same notional amount on the same set payment periods within the contract time. In the “plain vanilla” interest rate swap, the floating rate is the rate that prevails at the previous payment date, or in the case of the first payment, the rate at the opening of the contract. With LIBOR- in-arrears swaps, the floating rate paid on a payment date equals the rate observed on the payment date itself. Hence the floating leg cannot be valued as the sum of forward LIBORs.
Caplets and floorlets are the interest rate counterparts of European call and put options. Similar to vanilla swaps, the payoff of vanilla caplets and floorlets is based on the interest rate at the previous payment date whereas the payoff of in-arrears caplets and floorlets is based on the LIBOR rates at the actual time of the payment. Hence in-arrears derivatives are not as straightforward to price as their vanilla counterparts.
As stated by Chen and Sandmann [1] , typically when no assumptions are made about the term structure of interest rates, it is not possible to price these in-arrears products; and even when term structures are assumed, it is often not possible to find closed form solutions for the products. For this reason convexity adjustments (or convexity corrections) are often used by practitioners as a rule of thumb in the valuation of in-arrears term structure products. In [2] , Mallier and Alobaidi assume that risk-neutral interest rates follow the Cox-Ingersoll-Ross (CIR) model of the form
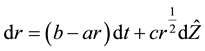
where a, b and c are constants and 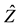 is a Wiener process under a risk-neutral probability measure. By using a Green’s function approach they manage to derive an analytical expression for in-arrears swaps.
is a Wiener process under a risk-neutral probability measure. By using a Green’s function approach they manage to derive an analytical expression for in-arrears swaps.
It has been shown (see e.g. [3] ) that when the short-term interest rate, r, follows a stochastic differential equation of the form
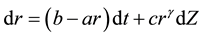
where a, b, γ and c are constants and dZ is an increment in a Wiener process under a real probability measure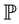 ; the value of γ is very important in differentiating between the different models’ abilities to adequately capture the dynamics of interest rates. In particular the unconstrained estimate of γ by Chan et al. [3] was 1.5. This was agreed upon by Campbell et al. [4] who showed that the heteroskedasticity of the short rate was markedly reduced as γ increased from 1 to 1.5. In [5] , Ahn and Gao showed that the interest rate model
; the value of γ is very important in differentiating between the different models’ abilities to adequately capture the dynamics of interest rates. In particular the unconstrained estimate of γ by Chan et al. [3] was 1.5. This was agreed upon by Campbell et al. [4] who showed that the heteroskedasticity of the short rate was markedly reduced as γ increased from 1 to 1.5. In [5] , Ahn and Gao showed that the interest rate model
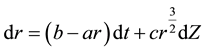 (1)
(1)
outperformed many of the popular interest rate models including the Vasicek and CIR models. The nonlinear drift in (1) implies a substantial nonlinear mean-reverting behaviour when the interest rate is above its long-run mean. Hence after a large interest rate rise, the interest rate can potentially quickly decrease, while after a low interest rate period, it can be slow to increase. It has also been shown that with a > 0, r will always remain positive. This model was further improved (see e.g. [6] [7] )
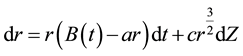 (2)
(2)
to include a time-dependent long-run target allowing yield-curves to be fitted.
In [6] , a solution was found for the price of bonds with maturity T, under the assumption that the risk-neutral process for r has a similar form to (2), namely
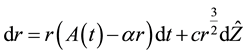 (3)
(3)
where 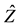 is a Wiener process under an equivalent risk-neutral measure
is a Wiener process under an equivalent risk-neutral measure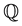 . The solution given is
. The solution given is
 (4a)
(4a)
where
 (4b)
(4b)
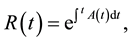 (4c)
(4c)
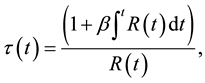 (4d)
(4d)
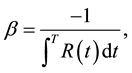 (4e)
(4e)
where 


subject to the final condition 


In Section 3 of this paper, we extend the results in [6] by finding an exact solution for in-arrears swaps under the assumption that risk-neutral interest rates follow the time-dependent 3/2 model (3). As is typical with swap pricing, we divide the swap into a series of forward rate agreements (FRAs) and price each of these individually. The value of the swap is the sum of the individual FRAs. This was also the approach of Mallier and Alobaidi [2] . Then in Section 4 we derive analytic approximations for caplets and floorlets based on the time-dependent interest rate model (3) and compare their values with those obtained using an accurate (but computationally intensive) numerical scheme. Firstly however, we briefly summarise Lie’s classical symmetries method which is used to solve the PDEs in this paper.
2. Lie’s Classical Symmetries Method
In essence, the classical method for finding symmetry reductions of a second-order PDE in one dependent variable V and two independent variables (r, t)

is to find a one-parameter Lie group of transformations in infinitesimal form



which leaves (6) invariant. The coefficients 


where

are vector fields that span the associated Lie algebra, and are called the infinitesimal generators of the transformation (7a-c), and 


Then for known functions

which when solved as a first-order PDE by the method of characteristics, yields the functional form of the similarity solution in terms of an arbitrary function, i.e.
where
and where 

Further, for a final-value problem with the final condition 





3. LIBOR-in-Arrears Swaps
In this section we derive the analytic solution for the price of in-arrears swaps based on the risk-neutral interest rate model (3). The value given here is from the perspective of the receiver i.e. the investor who receives the fixed rate 

Theorem 1. The value of an in-arrears swap with notional value 1 and fixed rate r0 to a receiver with payment times Ti every half year, when the interest rate follows the risk-neutral process (3) is given by


and 
Proof. The value of an FRA to the investor who receives the fixed rate 




bond under (3) is already known (given by Equation (4a-e)), we need only find the solution to (5) subject to



With the help of the package Dimsym [12] , we find that PDE (5) has the symmetry with generator

where
and where 

In order for the final condition to satisfy (11) and the boundary conditions to be invariant we choose
noting that

Substitution of this functional form into (5) gives that 

subject to

Solving (16) for 
where

Undoing the change of variables we get the solution to 
4. Asymptotic Solution for Caplets
Again assuming equidistant payment times





















In this section we look at approximating the value of caplets and floorlets for short times to expiry, based on the risk-neutral interest rate model (3). We note that caplets and floorlets characteristically have short tenor, especially when the associated caps and floors have maturities of about one year. For simplicity we let 

With


subject to 





Substituting (18) into (17) we get

Upon equating coefficients of 


where

i..e 


r is near K, the second-order derivative with respect to r needs to be included in the differential system. We in-
troduce the inner variable 

This leads to the equation
i.e

where




We now expand

and substitute this form into (21). Equating terms of 

subject to


PDE (23) admits a six-dimensional finite Lie group of transformations (see e.g. [9] ). With consideration of the
initial and boundary conditions, we use the symmetry with generator
an invariant solution of the form 


1We use the results [14] that (i) if 




which needs to be solved subject to
Hence we get that 

Now collecting terms of 


subject to



The two-term inner expansion can then be found by
We then match the inner and outer solutions to get a solution that is uniformly valid by calculating “outer + inner − common” where “common” is that part of the solution that is common to both. In this case as 

In a similar way we get an approximate solution for the value of a floorlet with expiry T and fixed floor rate K as

To test our approximate solutions we numerically solve PDE (17) using the mathematics software package MAPLE [15] (which uses a centered implicit finite-difference scheme) with step sizes of 10−4 and use this as a proxy for the true solution. We note that obtaining such numerical values is very labour-intensive and computationally-intensive whereas our approximate values are fast and easy-to-implement. Firstly, to test the accuracy of the finite-difference scheme, we used the method to numerically solve for in-arrears swap values i.e. Equation (5) subject to the conditions for the swap as given in Section 3, and compared these values to the exact solution (12). Using the parameter values






Using the same parameter values as our testing procedure, i.e.


we computed signed percentage errors for caplet values i.e.
(28) and the “parity” value i.e “floorlet + swap” value using the exact value of the swap given by Equation (12) multiplied by −2, and the approximate floorlet value given in Equation (29). The results are listed in Table 1. Similarly in Table 2 are the percentage errors of the approximate floorlet solutions given by (29) and the parity values found from “caplet-swap”.
From Table 1 and Table 2 it can be seen that as expected, in general, the shorter times to expiry yield the more accurate results. In particular we note
Equation (28) yields values for caplets that are at-the-money (ATM) or in-the-money (ITM) that are above our exact values, with relative errors <1.1% for


For caplets that are ATM or ITM, the parity formula yields the more accurate results where the value is dominated by the exact swap value. ATM options are slightly overpriced and mostly ITM options are underpriced slightly.
Table 1. Signed percentage errors of caplet approximations with



Table 2. Signed percentage errors of floorlet approximations with



For the values of 
Equation (29) yields values for ATM and ITM floorlets with relative errors <0.65% for


For floorlets that are ITM, the parity formula yields the more accurate results where the value is dominated by the exact swap value.
For the values of r where floorlets are out-of-the money (OTM), the caplet values have small percentage errors but these are large in comparison to corresponding floorlet values producing very large parity percentage errors.
The results suggest that parity values would be best to price ATM and ITM caplets and ITM floorlets; their values mostly slightly underpricing compared to the exact solution, while Equation (28) could be used to price OTM caplets and Equation (29) used to price ATM and OTM floorlets; their values producing small percentage errors especially (and surprisingly) for the larger values of 

It should also be noted that similar percentage error results were found using other volatility coefficient values c.
5. Discussion
The form of an interest rate model is crucial in the subsequent modelling of interest rate products and the accuracy of their valuations. It has been shown empirically by a number of authors that the 3/2 model (3) outperforms many of the popular interest rate models, such as the Vasicek and CIR models, in its ability to capture the actual behaviour of the interest rate. Including a free function of time in the drift further enhances the model’s ability to capture the interest rate dynamics. In this paper we have assumed the risk-neutral interest rate model (3) and extended the results in [6] by finding an exact solution for the value of in-arrears swaps and approximate values for caplets and floorlets with short times to expiry. As noted previously, caplets and floorlets have characteristically short tenors especially when the maturity of the cap/floor to which they belong, is about one year. The approximate option values have been shown to produce small percentage errors and in particular the parity values “caplet = floorlet + swap” and “floorlet = caplet − swap” produce best results for ATM and ITM caplets and ITM floorlets.
References
- Chen, A. and Sandmann, K. (2009) In Arrear Term Structure Products: No Arbitrage Pricing Bounds and the Convexity Adjustments. http://www.finance.uni-bonn.de/pdf-datei/download-datei-11
- Mallier, R. and Alobaidi, G. (2004) Interest Rate Swaps under CIR. Journal of Computational and Applied Mathematics, 164-165, 543-554. http://dx.doi.org/10.1016/S0377-0427(03)00490-4
- Chan, K., Karolyi, A., Longstaff, F. and Sanders, A. (1992) Empirical Comparison of Alternate Models of the Short- Term Interest Rate. Journal of Finance, 47, 1209-1227. http://dx.doi.org/10.1111/j.1540-6261.1992.tb04011.x
- Campbell, J.Y., Lo, A.W. and MacKinlay, A.C. (1996) The Econometrics of Financial Markets. Princeton University Press, Princeton.
- Ahn, D. and Gao, B. (1999) A Parametric Nonlinear Model of Term Structure Dynamics. Review of Financial Studies, 12, 721-762. http://dx.doi.org/10.1093/rfs/12.4.721
- Goard, J. (2000) New Solutions to the Bond-Pricing Equation via Lie’s Classical Method. Mathematical and Computer Modelling, 32, 299-313. http://dx.doi.org/10.1016/S0895-7177(00)00136-9
- Goard, J.M. and Hansen, N. (2004) Comparison of the Performance of a Time-Dependent Short-Interest Rate Model with Time-Dependent Models. Applied Mathematical Finance, 11, 147-164. http://dx.doi.org/10.1080/13504860410001686034
- Abramowitz, M. and Stegun, I.A. (1965) Handbook of Mathematical Functions. Dover Publications, New York.
- Bluman, G.W. and Kumei, S. (1989) Symmetries and Differential Equations. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4757-4307-4
- Goard, J.M. (2003) Noninvariant Boundary Conditions. Applicable Analysis, 82, 473-481. http://dx.doi.org/10.1080/0003681031000109639
- Wilmott, P. (1997) Derivatives: The Theory and Practice of Financial Engineering. John Wiley and Sons, New York.
- Sherring, J. (1993) DIMSYM Users Manual. La Trobe University, Melbourne.
- Black, F. (1976) The Pricing of Commodity Contracts. Journal of Financial Economics, 3, 167-179. http://dx.doi.org/10.1016/0304-405X(76)90024-6
- Howison, S. (2005) Matched Asymptotic Expansions in Financial Engineering. Journal of Engineering Mathematics, 53, 385-406. http://dx.doi.org/10.1007/s10665-005-7716-z
- Maplesoft (2008) Maple 12 Users Manual. Maplesoft, Waterloo.













