Modern Economy
Vol.5 No.7(2014), Article
ID:47283,15
pages
DOI:10.4236/me.2014.57073
Dynamic Modeling of the Harvesting Function: The Conflicting Case
George Emm Halkos, George J. Papageorgiou
Laboratory of Operations Research, Department of Economics, University of Thessaly, Volos, Greece
Email: halkos@econ.uth.gr, gjpap@otenet.gr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 February 2014; revised 21 March 2014; accepted 15 April 2014
Abstract
This paper is concerned with the classic topic of intertemporal resource economics: the optimal harvesting of renewable natural resources over time by one and several resource extractors with conflicting interests. The traditional management model, dating back to Plourde [1] , is overlooked both in the simple case for which the resource stock is treated as a state variable and in the improved case for which the harvesting equipment is treated as a stock variable. As a result in the extended case, the equilibrium richer than the saddle point, with bifurcations and limit cycles, is possible. While the results of the enriched management case are consistent with the concept of the pulse fishing, as this concept is introduced by Clark [2] -[4] , in the conflicting case the conditions, under which the richer limit cycle equilibrium occurs, are not enough investigated. Therefore, we discuss conflicts as a game with two types of players involved: the traditional fishermen armed with the basic equipment and the heavy equipment users. Both players have a common depletion function, considered as harvesting, which is dependent together on personal effort and on intensity of equipment’s usage.
Keywords
Renewable Resources, Exploitation of Natural Resources, Optimal Control, Differential Games

1. Introduction
In environmental economics’ vast literature, one given important meaning is connected with the exploitation of natural resources. According to this literature strand, a regeneration function is involved, which is necessary to model the interactions between the nature and the human activities. In an important paper, Strobele [5] considers the whole environment as renewable natural resource and the damage done to nature is described by a downward shift in the regeneration function due to the industrial waste emission. In the same, but more restrictive, way, Hannesson [6] compares the optimality of the monopolistic and social planning extractions, finding that the monopolistic standing optimal stock of the resource (say the nature) may be either larger or smaller than that under the social planning.
Strobele and Wacker [7] extend the one species exploitation to multiple species in a predator prey model. They derive a modified golden rule of harvesting, applying optimal control theory. Their conclusions about the modified golden rule in the steady state are related with the additional productivity effects. Farmer [8] , reconsidering Mourmouras’ type overlapping generations’ model with renewable natural resources, shows that there exists a non-trivial stationary state which exhibits, by definition, intergenerational natural capital equality.
Natural resources harvesting differs from production. Economic literature of renewable resources, based on the foundations of Gordon [9] , Scott [10] and Smith [11] , suggests particular properties of the open-access natural resources which require tools of analysis beyond those supplied by elementary economic theory. Such an appropriate tool is the optimal control theory and the use of differential equations in dynamic systems (either in a continuous or in a discrete framework), which are of common use in most models that explain the optimal management of natural resources extraction. These systems depend on more than one parameter that measures different economic and biological characteristics of the exploited resource. So the structural stability is a key point to study in order to explore whether the qualitative dynamical properties of the system persist when its structure is perturbed. In this context, the study of the structural stability is the first step to follow the analysis of the system.
On the other hand, it is reasonable to consider the stock of any renewable resource as a capital stock and treat the exploitation of that resource in much the same way as one would treat accumulation of a capital stock. This has been done to some extent by Clark and Munro [3] , and Clark [4] , whose papers contain a discussion of this point of view. However, the analysis is much simpler than it appears in the literature especially since the interaction between markets and the natural biology dynamics has not been made clear. Furthermore renewable resources are commonly analyzed in the context of models where the growth of the renewable resource examined is affected by two factors: the size of the resource itself and the harvesting rate. This specification does not take into account that human activities other than harvesting may have an impact on the growth of the natural resource (Levhari and Withagen [12] ).
Some externalities may arise in maximum sustained yield programs of replenishable natural resource exploitation followed by two fundamental problems. The first is that the existence of a social discount factor (or interest rate) may cause the maximum sustained yield program to be non-optimal (Plourde [1] ). The second problem relates to many externalities which may be present in harvesting resources. The most significant of these externalities is the stock externality in production. That is, there is a potential misallocation of inputs in the production of natural resource product due to the fact that one input, the natural resource, contributes to production but may not receive payment, as nobody owns the resource.
An analysis of the biomass harvesting (like fisheries) must take into account the biological nature of fundamental capital, the renewable resource, and must recognize the common property feature of land or sea, so it must allow that the fundamental capital is the subject of exploitation. The problem of fishing industry has been tackled by economists giving attention to the common property characteristics associated with both the open access and the lack of proper property rights to the fishery industry (Gordon [9] , Bjrndal [13] ). A number of existing studies on fishery economics have paid attention to the form of properties: full rights or no rights at all (Smith [11] , Plourde [14] ). Both cases lead to unique Nash non-cooperative outcomes with the social planner’s outcome in the case of full rights and the open access in the case of no rights. The latter is the result of the tragedy of commons (for discussion see Clark and Munro [3] ).
The fishery model with adjustment costs, arisen from changes in control variable, has been solved by Liski et al. [15] , thus providing a link between stable limit cycle policies and increasing returns in harvesting.
The management model, presented here, is close to a Wirl’s [16] paper which analyses the stability of optimal renewable resource extraction programs. In the complementary Wirl’s paper the second state variable is the capital, while the harvesting function is thought as a function of effort, capital and resource stock. Choosing the cost parameter as a bifurcation variable he shows that the cyclical exploitation of renewable resources may be optimal. The crucial condition that drives this result is the possibility of growth of the biomass, which implies that the stock falls below the level that maximizes the sustainable yield.
The rest of the paper is organized as follows. Section 2 comments about cyclical strategies on renewable resources. Section 3 provides the commercial management model with some improvements. Section 4 introduces the game model with a common harvesting function and Section 5 concludes.
2. Cyclical Strategies in Harvesting Management
In the renewable resources management literature two possible optimal strategies are considered under stationary conditions (e.g. Plourde [14] , Clark [4] ). The first ones are the continuous time strategies, whereby the renewable resource is exploited at all times. Following this type of strategy, the resource stock is considered dependent on both economic and social conditions as regards the resource, the discount rate and finally the initial resource stock size. The implications of that strategy depend on the stationary size of the resource, for which the harvesting rate is decided (Lewis and Schmalensee [17] ). As it becomes clear―and as it is well known―the above strategy does not take into account (or neglects) the role of capital inflows taking place in the harvesting industry.
As already mentioned, one can consider as capital inflows the available fleets and the human capital employed, but a more interesting aspect is the ability to modify all the above capital factors involved in the harvesting. Another important reason to deviate from the original continuous time strategy is the argument raised by some authors (e.g. Clark [4] , Dawid and Kopel [18] ), which states that harvesting strategies that stabilize the stock of the renewable resource to a usual steady state level may be replaced by policies involving the abandonment or cyclical utilization of the resource (Liski et al. [15] ).
This second strategy, already discussed in harvesting management literature, involves extinction or abandonment policies, implying that, after a finite time, harvesting is abandoned forever (Lewis and Schmalensee [17] ). A first valuable insight for this type of optimal strategy is the fact that cyclical fishing policies are observed in practice. Moreover, Bjrndal [13] uses data covering years 1952-1972 to show a relatively regular cyclical pattern for harvesting. In harvesting management, one possible optimal cyclical harvest policy, well known as chattering strategies or pulse fishing (Liski et al. [15] ), is incorporated with the fleets’ withdrawal and reentry as well as by hiring and firing workers, thus implying cost fluctuations.
Chattering strategies, in fishery management, are also subject to adjustment costs since the harvest rate and the costs incurred (startup and reentry costs) are independent of each other. The size of adjustment costs plays a crucial role in the optimal harvesting policies. Especially in the case of relatively modest adjustment costs, it has been shown that all conceivable policies will exhibit a limit cycle policy over time, which not only exists but it is also stable. One important result obtained from the above chattering policy is the fact that the cyclical utilization of the resource is related to smooth fluctuations and not to complete shutdowns of the fishery management. The economic implication of the cyclical harvesting policy existence is summarized as the profitable advantage of increasing returns by temporarily harvesting excessive quantities and stabilizing the stock of fish over time by cutting the harvest rate back after each period of excessive harvesting (Liski et al. [15] ).
It is also worth noting that the above given implication is valid only for low adjustment costs; otherwise, for high adjustment costs, it is preferable to follow the saddle point stability with a constant harvest rate. The importance of cyclical policies in harvesting, also known as pulse fishing policies, is confirmed by Wirl’s model [16] , whereby the resulting cyclical strategy is related to the positive externality of the stock. Moreover, in the same paper, Wirl obtains saddle point stability for low adjustment costs contrary to the results obtained by Liski et al. [15] .
While the importance of pulse fishing policies is well understood in the management context, the possibility of limit cycle policies in the conflicting approach has not been previously addressed, at least to our knowledge. Therefore, in order to achieve realism, we suggest a simple game model between two types of players: the crowd of the negligible capital investment fishermen, using a single boat for their fishing effort, and the heavily equipped players, using a fleet of vessels, hence facing adjustment costs. As it becomes clear, the crowd of the first type, thought as one player, has all the prerequisites (i.e. negligible adjustment costs and increasing returns) to follow the profitable cyclical patterns as identified in the management case, but it is not certain that their costs remain negligible due to the presence of the heavily equipped rivals in the same harvesting arena. Supposing that they adhere to the cyclical fishing policy, as the proven profitable solution for them, they take the corresponding substantial risk.
On the other side, the heavily equipped players, using fleets and workingmen and therefore facing adjustment costs, decide to follow the same profitable cyclical pattern, lowering their adjustment costs as much as possible. Since the low adjustment cost is the basic prerequisite to follow a cyclical pattern it is reasonable to internalize the above cost inside the intensity of their fleet usage. In the suggested conflict between the two types of players, the basic supposition is that the players adhere to the cyclical patterns, as they are considered the only profitable policies that stabilize the resource stock. In this way, the suggested model contributes to the existing harvesting management literature in the conflicting sense, clarifying the conditions under which the desired cyclical policies are obtained.
3. The Management of Commercial Harvesting
In the traditional case model, also studied for instance by Clark and which goes back to the very simple Gordon Schaeffer model, 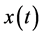 is the resource stock at time
is the resource stock at time ,
,  the resource’s harvesting function and
the resource’s harvesting function and  the regeneration function of the natural resource. With these functions in the model one obtain the system dynamics, as
the regeneration function of the natural resource. With these functions in the model one obtain the system dynamics, as
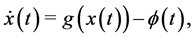 (3.1)
(3.1)
The goal of the decision maker is to maximize the discounted utility derived over the infinite planning interval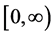 . That is, the objective functional is given as:
. That is, the objective functional is given as:
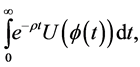 (3.2)
(3.2)
where 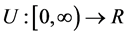 is the utility function. Concerning equilibrium, in this reference one state model, it has been shown that the optimal management admits a unique equilibrium path which converges to the saddle point (see for example Dockner et al. [19] ).
is the utility function. Concerning equilibrium, in this reference one state model, it has been shown that the optimal management admits a unique equilibrium path which converges to the saddle point (see for example Dockner et al. [19] ).
On the other hand, commercial extraction of natural resources in an intensive rate requires sometimes improvements on the harvesting equipment in order to be efficient. In this improved case one can treat the harvesting effort not as an instantaneous control but rather as a stock variable. Integrating over past adjustments the new control variable  enters into the model, describing the evolution of the harvesting effort.
enters into the model, describing the evolution of the harvesting effort.
Considering harvesting as a stock variable, some modifications are necessary to made in the objective functional, that is the introduction of the adjustment costs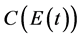 , for the new stock. In this subsection, as the analysis it is well known e.g. Liski et al. [15] , we briefly discuss a concave natural resources regeneration function
, for the new stock. In this subsection, as the analysis it is well known e.g. Liski et al. [15] , we briefly discuss a concave natural resources regeneration function . The concavity of the function
. The concavity of the function 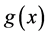 states that the law of diminishing returns applies here too. Moreover the utility enjoyed by the representative agent is a function depending on the harvest
states that the law of diminishing returns applies here too. Moreover the utility enjoyed by the representative agent is a function depending on the harvest 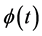 and on the existing resource stock, as well. With these modifications the optimal management problem becomes
and on the existing resource stock, as well. With these modifications the optimal management problem becomes
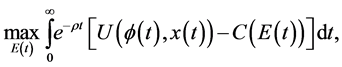 (3.3)
(3.3)
subject to
 (3.4)
(3.4)
 (3.5)
(3.5)
Model (3.4)-(3.5) is an optimal control with two state and one control variable and with a quadratic cost function. In the solution process the possibility of limit cycles appearance in such models with two state variables was established by Dockner and Feichtinger [20] .
Using the quadratic cost function 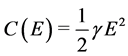 with
with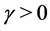 , finally the conditions that determine the optimal plan of a central decision maker, after the appropriate substitutions, are (time is neglected to avoid notational overburdening):
, finally the conditions that determine the optimal plan of a central decision maker, after the appropriate substitutions, are (time is neglected to avoid notational overburdening):
 (3.6)
(3.6)
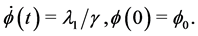 (3.7)
(3.7)
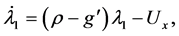 (3.8)
(3.8)
 (3.9)
(3.9)
The study of the dynamic properties of system (3.6)-(3.9) includes stability of the system which is restricted to saddle point stability, i.e. to a two dimensional manifold in the four dimensional space of state and costates. According to Dockner’s explicit formula (Dockner [21] ) the four eigenvalues ,
, ![]() of the linearized dynamics of the canonical equations are given by:
of the linearized dynamics of the canonical equations are given by:
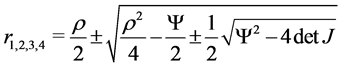 (3.10)
(3.10)
and the magnitude ![]() is the sum of determinants of submatrices of the Jacobian
is the sum of determinants of submatrices of the Jacobian ![]() expressed as:
expressed as:
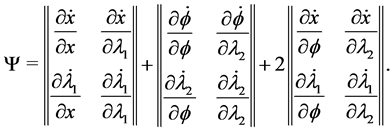 (3.11)
(3.11)
From Dockner’s formula (3.10), it is well known that sufficient conditions for the saddle point are first the positive determinant of the Jacobian matrix and secondly the negativity of the coefficient ![]() given by (3.11). A positive determinant of the Jacobian is crucial for stability, because a negative determinant restricts the stability to a one dimensional manifold of initial conditions (with one negative eigenvalue, the other three are positive or have positive real parts) and the generic solution is unstable. Figure 1, also published by Dockner and Feichtinger [20] , classifies the eigenvalues depending on the determinant of
given by (3.11). A positive determinant of the Jacobian is crucial for stability, because a negative determinant restricts the stability to a one dimensional manifold of initial conditions (with one negative eigenvalue, the other three are positive or have positive real parts) and the generic solution is unstable. Figure 1, also published by Dockner and Feichtinger [20] , classifies the eigenvalues depending on the determinant of  and
and![]() .
.
Considering the discount rate ![]() as a parameter, the values of
as a parameter, the values of ![]() for which the conditions are met, are possible Hopf bifurcations1 (Kuznetsov, [22] ) and a limit cycle will emerge if the complex eigenvalues
for which the conditions are met, are possible Hopf bifurcations1 (Kuznetsov, [22] ) and a limit cycle will emerge if the complex eigenvalues  cross the imaginary axis with non-zero velocity at
cross the imaginary axis with non-zero velocity at
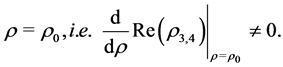
Hence, in the case of growth , the suppositions of the logistic growth
, the suppositions of the logistic growth ,
,  and
and  are sufficient to ensure saddle point stability, (
are sufficient to ensure saddle point stability, ( ), but the local monotonicity is not implied.
), but the local monotonicity is not implied.
3.1. The Incentive for Fleet Modifications
As a continuation of the known previous discussion about commercial harvesting, the basic two dimensional management problem consisting of Equations (3.3)-(3.5), can also be modified more in the case the available equipment is subject to expansions or reductions. As harvesting equipment, can be considered the available fleet, electronic machines, boats, nets, workmen hiring and so forth. Equipment’s modifications are also highly dependent on the existing renewable resource stock and it can be seen as a stock as well, which affects directly the harvesting function .
.
Therefore one can treat the harvesting function  as a function of the accumulated equipment,
as a function of the accumulated equipment, . The accumulated equipment
. The accumulated equipment , does not, however, remain at a fixed level, but is also subject to depreciation, which entails at a simple depreciation rate and moreover it is reasonable to argue that the renewable resource extractor enjoys utility from the decision to modify the equipment. The modifications that are possible to make in the original model are first, in the objective functional which enters in an additively separable utility form and, second in the two equations of motion. Setting harvesting equipment as a state variable, the decision to expand (or to reduce) would be now the new control which enters into the system.
, does not, however, remain at a fixed level, but is also subject to depreciation, which entails at a simple depreciation rate and moreover it is reasonable to argue that the renewable resource extractor enjoys utility from the decision to modify the equipment. The modifications that are possible to make in the original model are first, in the objective functional which enters in an additively separable utility form and, second in the two equations of motion. Setting harvesting equipment as a state variable, the decision to expand (or to reduce) would be now the new control which enters into the system.
After all the simplified assumptions, the original optimal control problem (3.3)-(3.5) now becomes
 (3.12)
(3.12)
subject to
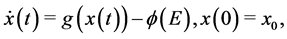 (3.13)
(3.13)
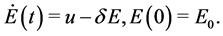 (3.14)
(3.14)
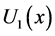 ,
, 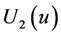 represent utility in separable form, consisting of the utility derived from the existing renewable resource stock and from agent’s decision
represent utility in separable form, consisting of the utility derived from the existing renewable resource stock and from agent’s decision  to modify his equipment. The harvesting function
to modify his equipment. The harvesting function 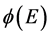 is denoted as a function of the available equipment, while
is denoted as a function of the available equipment, while ![]() is the equipment’s depreciation rate. The control
is the equipment’s depreciation rate. The control 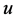 influences directly equipment’s changes, but also has an indirect effect on the renewable resource stock via the harvesting
influences directly equipment’s changes, but also has an indirect effect on the renewable resource stock via the harvesting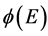 .
.
Moreover the representative agent faces an intertemporal trade off between the benefits associated with the stock 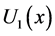 and the benefits resulting from fleet’s expansion or reduction
and the benefits resulting from fleet’s expansion or reduction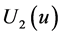 . It is worth noting that the second part of utility
. It is worth noting that the second part of utility  is the net value, which captures all the costs associated with the expansion or reduction. Finally, the decision to modify equipment,
is the net value, which captures all the costs associated with the expansion or reduction. Finally, the decision to modify equipment, 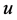 , is maybe positive in the case of expansion or negative in the case of reduction, which also means that the depreciation parameter
, is maybe positive in the case of expansion or negative in the case of reduction, which also means that the depreciation parameter ![]() can be set to zero at the steady state equilibrium implying
can be set to zero at the steady state equilibrium implying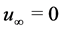 , i.e. no equipment’s modification made in equilibrium.
, i.e. no equipment’s modification made in equilibrium.
In the solution process, the following two equations determine the evolution of the costates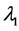 ,
, ![]() ,
,
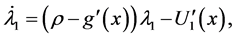 (3.15)
(3.15)
 (3.16)
(3.16)
Equations (3.15)-(3.16) together with the two equations of motion (3.13)-(3.14) constitutes the following canonical system of necessary conditions
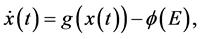 (3.17)
(3.17)
 (3.18)
(3.18)
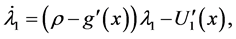 (3.19)
(3.19)
 (3.20)
(3.20)
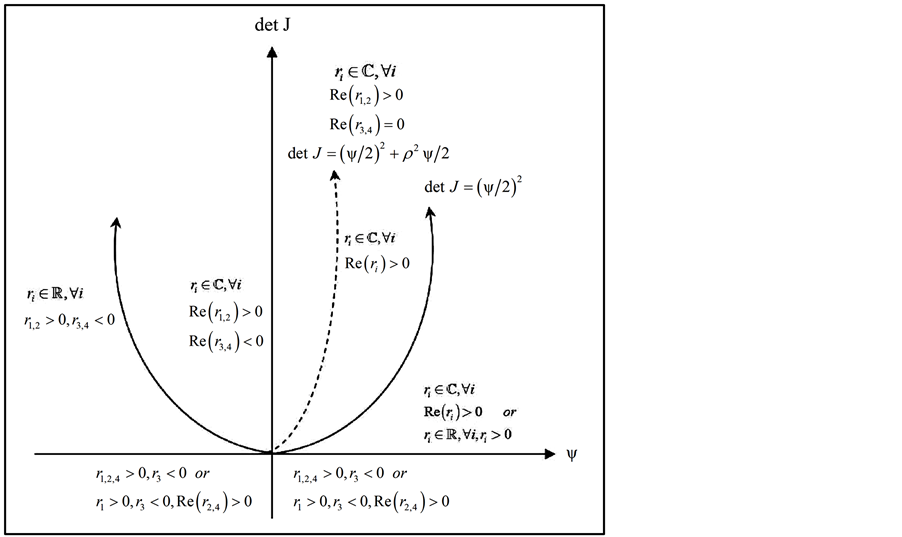
Figure 1. Classification of the eigenvalues depending on detJ and Ψ.
and the corresponding Jacobian becomes

Again we may apply Formula (3.10) to compute the four eigenvalues of the above Jacobian, which are crucial to characterize the local dynamics of the linear ODE that approximates the canonical Equations (3.17)-(3.20). But now Formula’s (3.10) coefficient ![]() reduces to
reduces to
 (3.21)
(3.21)
and the determinant of the Jacobian evaluated at the equilibrium is given by
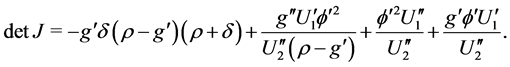 (3.22)
(3.22)
The stability properties of this optimally controlled system depends on the sign of the growth’s function rate of change ![]() (evaluated at the steady state) and on the other model characteristics in the following way.
(evaluated at the steady state) and on the other model characteristics in the following way.
Case 1: 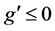 and the long-run equilibrium is a saddle point. The result follows directly from (3.22), since
and the long-run equilibrium is a saddle point. The result follows directly from (3.22), since 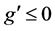 implies
implies ![]() and
and![]() . Therefore, two eigenvalues must have negative real parts.
. Therefore, two eigenvalues must have negative real parts.
Case 2: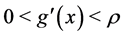 , the long-run equilibrium is characterized by all different cases, i.e. saddle point stability, locally unstable spirals and instability such that convergence to the equilibrium is restricted to a one dimensional set of initial conditions. According to Poincare-Andronov-Hopf (PAH) theorem, the transition from a domain of stable to locally unstable may give rise to limit cycles.
, the long-run equilibrium is characterized by all different cases, i.e. saddle point stability, locally unstable spirals and instability such that convergence to the equilibrium is restricted to a one dimensional set of initial conditions. According to Poincare-Andronov-Hopf (PAH) theorem, the transition from a domain of stable to locally unstable may give rise to limit cycles.
Under the supposition of growth, 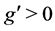 (Case 2), and a diffusion process with one and only one point
(Case 2), and a diffusion process with one and only one point ![]() such that
such that , it is well known that the time path of the renewable resource level consists of a convex segment (if
, it is well known that the time path of the renewable resource level consists of a convex segment (if![]() ) and a concave segment (if
) and a concave segment (if![]() ). In other words, the domain of the low level
). In other words, the domain of the low level 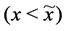 exhibits increasing returns and the domain of high level is characterized by diminishing returns. It is plausible that diminishing returns lead to stable equilibrium, whereas increasing returns favour complexities, i.e. limit cycles. The reason is that a low level of resource may increase to a certain threshold so it may be rational for the agent to expand his equipment to gain future benefits.
exhibits increasing returns and the domain of high level is characterized by diminishing returns. It is plausible that diminishing returns lead to stable equilibrium, whereas increasing returns favour complexities, i.e. limit cycles. The reason is that a low level of resource may increase to a certain threshold so it may be rational for the agent to expand his equipment to gain future benefits.
3.2. Specifications
We assume benefits stemming from the existing renewable resource stock to be proportional to its current level. Moreover the growth of benefits associated with the current accumulated level of equipment’s expansion is, however, not unrestricted but rather reaches a maximum level. After all we specify the functional forms as follows:
 (3.23)
(3.23)
 (3.24)
(3.24)
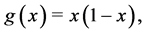 (3.25)
(3.25)
 (3.26)
(3.26)
The last two equations represent the fact that a maximum level of the resource exists towards which 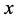 grows in the absence of harvesting, while the decline of the resource’s level is proportional to the accumulated level of equipment
grows in the absence of harvesting, while the decline of the resource’s level is proportional to the accumulated level of equipment . But, in the long run, the decision for modifications has a relative small meaning due to the high depreciation that has been made on to the past accumulated equipment. That is, at the steady state, the decision,
. But, in the long run, the decision for modifications has a relative small meaning due to the high depreciation that has been made on to the past accumulated equipment. That is, at the steady state, the decision, ![]() , tends to zero and this result is attained only setting the depreciation rate very close to zero,
, tends to zero and this result is attained only setting the depreciation rate very close to zero,![]() . With the last supposition and under specifications (3.23)-(3.26) the determinant of the Jacobian (3.22) and coefficient
. With the last supposition and under specifications (3.23)-(3.26) the determinant of the Jacobian (3.22) and coefficient ![]() (3.21) reduces to
(3.21) reduces to
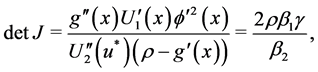 (3.27)
(3.27)
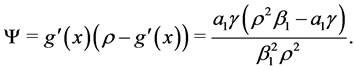 (3.28)
(3.28)
Having the set of necessary requisites for a pair of purely imaginary eigenvalues existence, i.e.
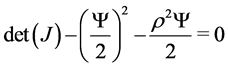 ,
, ![]() and
and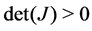 , we continue choosing
, we continue choosing  as the bifurcation point for the certain parameter values
as the bifurcation point for the certain parameter values ,
,  ,
,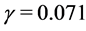 . Considering the dynamical system, it can be shown numerically (Grass et al. [23] ), for the above values of parameters, the conditions for complex eigenvalues with positive real parts are met for
. Considering the dynamical system, it can be shown numerically (Grass et al. [23] ), for the above values of parameters, the conditions for complex eigenvalues with positive real parts are met for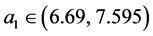 , and moreover stable limit cycles exist, at least in the right-hand vicinity of
, and moreover stable limit cycles exist, at least in the right-hand vicinity of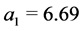 . Figure 2 shows the phase portrait in the modification stock plane that corresponds to the above values of
. Figure 2 shows the phase portrait in the modification stock plane that corresponds to the above values of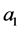 . In Figure 2 the four phases I-IV characterize the cycle as optimal strategy in the management problem. That is:
. In Figure 2 the four phases I-IV characterize the cycle as optimal strategy in the management problem. That is:
![]() and
and![]() .
.
![]() and
and![]() .
.
![]() and
and![]() .
.
![]() and
and![]() .
.
Starting with a minimum level of renewable resource stock, Phase I is characterized by reduction in equipment ![]() but at a diminishing rate
but at a diminishing rate![]() . This process implies that, in the same Phase I, decision
. This process implies that, in the same Phase I, decision  becomes positive at some time instant and continues to grow for sufficient level of the resource stock. In Phase II equipment expands yet when resource stock is still rising to its peak. In Phase III since the renewable resource stock peaks its maximum value the agent exploits the large stock, but equipment’s high expansion now affects the resource stock which declines, so a decision to reduce equipment is taken. Finally, in Phase IV, decision
becomes positive at some time instant and continues to grow for sufficient level of the resource stock. In Phase II equipment expands yet when resource stock is still rising to its peak. In Phase III since the renewable resource stock peaks its maximum value the agent exploits the large stock, but equipment’s high expansion now affects the resource stock which declines, so a decision to reduce equipment is taken. Finally, in Phase IV, decision 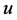 becomes negative, meaning equipment’s reduction, and the resource stock stops the downward fall.
becomes negative, meaning equipment’s reduction, and the resource stock stops the downward fall.

Figure 2. Phase portrait of the example of a cyclical strategy in a decision-stock plane.
4. Conflicts with a Common Harvesting Function
Let us, as before, denote by  the instantaneous renewable resource which is in common access at time
the instantaneous renewable resource which is in common access at time . Without any harvesting taking place the stock of resources grows according to the function
. Without any harvesting taking place the stock of resources grows according to the function , obviously depending on the resource itself, satisfying the conditions
, obviously depending on the resource itself, satisfying the conditions ,
, 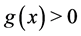 for all
for all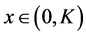 ,
,  for all
for all ,
, . In the game that follows we assume that two types of players are involved. First is the renewable resource extractors (players) acting with the traditional mode in the sense of Clark [4] , with the latter implying that they are armed with the basic equipment, usually harvests only personally, but there is a crowd of this type of players. Second are the commercial heavy equipment users with a lot of vessels usually acting as factories. Carrying out harvesting is costly for the second type of players, e.g. damages in the available equipment, payroll for workingmen, also reducing its financial capital.
. In the game that follows we assume that two types of players are involved. First is the renewable resource extractors (players) acting with the traditional mode in the sense of Clark [4] , with the latter implying that they are armed with the basic equipment, usually harvests only personally, but there is a crowd of this type of players. Second are the commercial heavy equipment users with a lot of vessels usually acting as factories. Carrying out harvesting is costly for the second type of players, e.g. damages in the available equipment, payroll for workingmen, also reducing its financial capital.
Considering now the depletion of the renewable resource stock (the harvesting function), one can think that however, does not only depend on the intensive usage 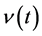 of the heavy equipped player, but is also influenced by the other players’ overall effort
of the heavy equipped player, but is also influenced by the other players’ overall effort  which act traditionally. We set as instrument variables the intensity of equipment and the personal harvesting effort respectively i.e. for the heavy equipped player (player type 2), the intensity of the harvesting equipment’s usage
which act traditionally. We set as instrument variables the intensity of equipment and the personal harvesting effort respectively i.e. for the heavy equipped player (player type 2), the intensity of the harvesting equipment’s usage , and the for traditional fishermen (players of kind 1), its personal effort
, and the for traditional fishermen (players of kind 1), its personal effort , both assumed non-negatives
, both assumed non-negatives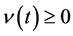 ,
,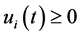 .
.
We denote the overall harvesting function by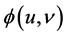 , also depending on both overall effort
, also depending on both overall effort 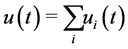 and on intensity. Combining the growth
and on intensity. Combining the growth 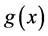 with the harvesting function
with the harvesting function  the state dynamics can be written as
the state dynamics can be written as
 (4.1)
(4.1)
Along a trajectory the non-negativity constraint is imposed, that is
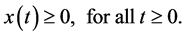 (4.2)
(4.2)
A higher intensity of harvesting equipment usage (for player 2) and also the effort of the crowd of traditionally acting fishermen (player 1) certainly leads to stronger depletion of the renewable resource, so it is enough reasonable to assume that the partial derivatives of the harvesting function to be positive with respect to the parameters, i.e. ,
, . Moreover the law of diminishing returns is applied only for the type 1 player’s effort undertaken, that is
. Moreover the law of diminishing returns is applied only for the type 1 player’s effort undertaken, that is 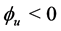 and for simplicity we assume
and for simplicity we assume . Additionally, we assume that the Inada conditions, which guarantee that the optimal strategies are nonnegative, holds true, i.e.
. Additionally, we assume that the Inada conditions, which guarantee that the optimal strategies are nonnegative, holds true, i.e.
 (4.3)
(4.3)
The utility functions the two players want to maximize are defined as follows: player 1, the representative traditional fisherman, derives instantaneous utility, on one hand from its own harvesting product, but its personal effort  gives rise to increasing and convex costs
gives rise to increasing and convex costs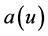 , and on the other hand from the high stock of renewable resource also denoted by the increasing function
, and on the other hand from the high stock of renewable resource also denoted by the increasing function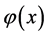 . After all the present value of player’s 1 utility is described by the following functional
. After all the present value of player’s 1 utility is described by the following functional
 (4.4)
(4.4)
Player 2, the heavy equipped, enjoys utility  from the renewable resource stock
from the renewable resource stock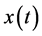 , but also from their equipment’s intensity of use
, but also from their equipment’s intensity of use , which is described by the function
, which is described by the function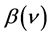 . For the utilities
. For the utilities 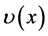 and
and  we assume that they are monotonically increasing functions with decreasing marginal returns, that is
we assume that they are monotonically increasing functions with decreasing marginal returns, that is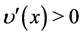 ,
, 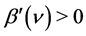 and
and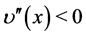 ,
, . We also assume that the individually acting players’ overall effort
. We also assume that the individually acting players’ overall effort  has no impact on player’s 2 utility. So, player’s 2 utility function is defined, in additively separable form, as:
has no impact on player’s 2 utility. So, player’s 2 utility function is defined, in additively separable form, as:
 (4.5)
(4.5)
4.1. Periodic Solutions
Let us now explore whether periodic solutions are possible, starting with steady state and stability analysis of necessary conditions. As it is clear the problem can be treated as a differential game with two controls and one state. Corresponding Hamiltonians, optimality conditions and adjoint variables for the problem under consideration are respectively:
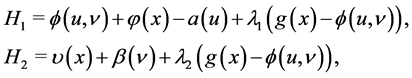
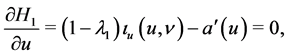 (4.6)
(4.6)
 (4.7)
(4.7)
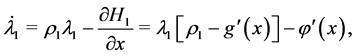 (4.8)
(4.8)
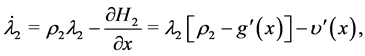 (4.9)
(4.9)
where subscripts denote player 1 and player 2 respectively for Hamiltonias  and adjoints
and adjoints ,
,![]() . Steady state solutions for the state, adjoints and controls are solutions of the system of equations:
. Steady state solutions for the state, adjoints and controls are solutions of the system of equations:
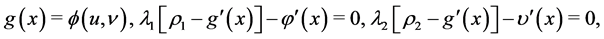
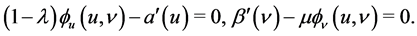
The Jacobian matrix of the system of optimality conditions is the following

which also gives: 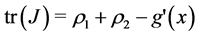 and
and

According to Wirl [24] (proposition 4) the existence of a pair of purely imaginary eigenvalues requires that the following conditions are satisfied:

where coefficient  is the result of the sum of the following determinants
is the result of the sum of the following determinants
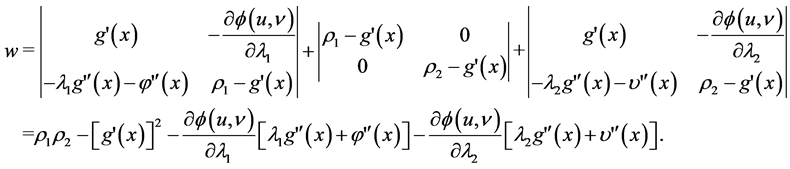
From now on the crucial condition for cyclical strategies (precisely for Hopf bifurcations to occur) is that![]() ,
, 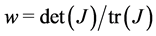 , which after simple algebraic calculations reduces to
, which after simple algebraic calculations reduces to
 (4.10)
(4.10)
4.2. Specifications for the Game
We specify the functions of the game as follows: a diffusion process for the renewable resource growth function, that is , a Cobb Douglas type function for the harvesting
, a Cobb Douglas type function for the harvesting  and the utility function stemming from equipment’s intensive use of player 2 in the form
and the utility function stemming from equipment’s intensive use of player 2 in the form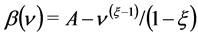 . Note that the utility function
. Note that the utility function 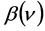 with
with ![]() and
and  exhibits constant relative risk aversion in the sense of Arrow-Pratt measure of risk aversion. All the other functions are left in a linear form, i.e. both utilities stemming from the existing renewable resource stock are for player 1
exhibits constant relative risk aversion in the sense of Arrow-Pratt measure of risk aversion. All the other functions are left in a linear form, i.e. both utilities stemming from the existing renewable resource stock are for player 1 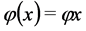 and for player 2
and for player 2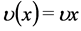 , while the player’s 1 effort cost in the linear fashion
, while the player’s 1 effort cost in the linear fashion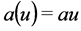 , as well. Note that all the involved coefficients, i.e. the intrinsic growth rate
, as well. Note that all the involved coefficients, i.e. the intrinsic growth rate  and the slopes
and the slopes ![]() and
and 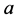 are positive real numbers, but
are positive real numbers, but 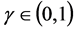 and
and ![]() and
and , as already mentioned. With the above specifications the following result holds true.
, as already mentioned. With the above specifications the following result holds true.
Proposition 4.1. A necessary condition for cyclical strategies in the game between traditionally acting and heavy equipped players, as described above, is the heavy equipped players are more impatient than the simple traditionally acting.
Proof. See in the Appendix. □
The intuition behind proposition 4.1 is straightforward. We start with a rather low and increasing intensity of equipment usage on behalf of the heavy equipped players. The traditionally acting players operate at a low effort, as well, because the increasing effort incurs costs, but they are worrying about the renewable resource level, consequently for their jobs, by reason of the player 2 presence. Now suppose that the heavy equipped react as a farsighted, he would increase the equipment’s intensity only moderately and the dynamical system would approach a stable steady state. But, due to their impatience they behave myopically and react by strongly increasing the intensity of their machines. At this time the crowd of the traditionally acting players, has only two choices: to loose their jobs or to increase their overall effort. Suppose that they stay in the harvesting increasing their overall effort, but the latter means that the combination of high intensity on behalf of the heavy equipped and the higher effort on behalf of the crowd leads to a strong reduction of the renewable resource stock.
But the low level of the resource stock is unprofitable for the heavy equipped to work at a high intensity, therefore they have to decrease intensity and the cycle is closed. A new cycle starts again, possibly in another place because of the stock’s reduction, but with the same results also described. In our opinion the crucial point of this intuitive explanation is that player’s 1 strategic variable 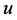 lags behind player’s 2 strategic variable
lags behind player’s 2 strategic variable 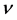 and both are lagged behind the state variable, the renewable resource’s stock
and both are lagged behind the state variable, the renewable resource’s stock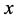 .
.
5. Conclusions
In environmental economics the exploitation of renewable resources is a well overlooked field since the original model, dated back to Schafer [25] . As it is well known that the analysis concentrates on the two basic factors that affect the fishing industry, namely the size of the resource itself and the rate of human harvesting. The above specification does not take into account any other human activities which affect biomass, for example coastlines pollution. Concerning longrun equilibrium, as it is well known, the simplest case of the saddle-point type stability requires only one characteristic of the renewable resource’s growth function, which is the negative growth. But even the supposition of negative growth is sufficient for the saddle-point stability, the local monotonicity is not implied i.e. transient cycles may occur.
On the other hand, harvesting management is not restricted in the traditional way of the renewable resource extraction in the sense of one-man show. Commercial harvesting often requires investment and disinvestment in equipment, and the undertaken decision to expand or to reduce equipment obeys onto the state variable which is the existing renewable resource stock. Therefore, concerning harvesting, as a stock variable, equilibrium dynamics become more complex, and much richer, also including saddle point stability. The dynamics of such equilibrium reveal cyclical policies as optimal strategies.
The emphasis given in the paper is not restricted on the stability properties of the optimal management program, but we also focus on the stability properties of the induced nonzero sum game between two types of players which share a common depletion function thought as a harvesting. Precisely, the game set up between a crowd of weakly armed and a strongly armed player with a common depletion function yields an economic result, for which the discount rate plays the crucial role for periodic solutions. That is, the condition for periodic solutions is that the strong equipped player is more impatient than the weak.
Acknowledgements
An earlier version of this paper was presented in Thales Research Workshop entitled “Optimal Management of Dynamic Systems of the Economy and the Environment” that took place in September 28, 2012 in Kostis Palamas building of the National and Kapodestrian University of Athens. Thanks are due to Professor A. Xepapadeas and the participants in the workshop for helpful comments and discussions. Any remaining errors are solely the authors responsibility.
References
- Plourde, C.G. (1970) A Simple Model of Replenishable Natural Resource Exploitation. American Economic Review, 62, 518-521.
- Clark, C. (1973) Profit Maximization and the Extinction of Animal Species. Journal of Political Economy, 81, 950-961. http://dx.doi.org/10.1086/260090
- Clark, C.W. and Munro, G.R. (1975) Economics of Fishing and Modern Capital Theory: A Simplified Approach. Journal of Environmental Economics and Management, 2, 92-106.
http://dx.doi.org/10.1016/0095-0696(75)90002-9 - Clark, C. (1990) Mathematical Bioeconomics. 2nd Edition, Wiley Interscience, Hoboken.
- Strobele, W. (1988) The Optimal Intertemporal Decision in Industrial Production and Harvesting a Renewable Natural Resource. Journal of Economics, 48, 375-388.
http://dx.doi.org/10.1007/BF01227543 - Hannesson, R. (1983) A Note on Socially Optimum versus Monopolistic Exploitation of a Renewable Resource. Journal of Economics, 43, 63-70. http://dx.doi.org/10.1007/BF01283884
- Strobele, W. and Wacker, H. (1995) The Economics of Harvesting Predator-Prey Systems. Journal of Economic, 61, 65-81. http://dx.doi.org/10.1007/BF01231484
- Farmer, K. (2000) Intergenerational Natural Capital Equality in an Overlapping Generations Model with Logistic Regeneration. Journal of Economics, 72, 129-152.
http://dx.doi.org/10.1007/BF01676980 - Gordon, H.S. (1954) The Economic Theory of a Common Property Resource. Journal of Political Economics, 62, 124-142. http://dx.doi.org/10.1086/257497
- Scott, A. (1955) Natural Resources: The Economics of Conservation. University of Toronto Press, Toronto.
- Smith, V.L. (1969) On Models of Commercial Fishing. Journal Political Economy, 77, 181-198. http://dx.doi.org/10.1086/259507
- Levhari, D. and Withagen, C. (1992) Optimal Management of the Growth Potential of Renewable Resources. Journal of Economics, 3, 297-309. http://dx.doi.org/10.1007/BF01237184
- Bjrndal, T. (1987) Production Economics and Optimal Stock Size in a North Atlantic Fishery. Scandinavian Journal of Economics, 89, 145-164. http://dx.doi.org/10.2307/3440061
- Plourde, C.G. (1971) Exploitation of Common Property Replenishable Resources. Western Economic Journal, 9, 256-266.
- Liski, M., Kort, P. and Novak, A. (2001) Increasing Returns and Cycles in Fishing. Resource and Energy Economics, 23, 241-258. http://dx.doi.org/10.1016/S0928-7655(01)00038-0
- Wirl, F. (1995) The Cyclical Exploitation of Renewable Resource Stock May Be Optimal. Journal of Environmental Economics and Management, 29, 252-261. http://dx.doi.org/10.1006/jeem.1995.1045
- Lewis, T. and Schmalensee, R. (1979) Non-Convexity and Optimal Harvesting Strategies for Renewable Resources. Canadian Journal of Economics, 12, 677-691.
http://dx.doi.org/10.2307/134873 - Dawid, H. and Kopel, M. (1997) On the Economically Optimal Exploitation of a Renewable Resource: The Case of a Convex Environment and a Convex Return Function. Journal of Economic Theory, 76, 272-297. http://dx.doi.org/10.1006/jeth.1997.2305
- Dockner, E., Jorgensen, S., Long, N.V. and Sorger, G. (2000) Differential Games in Economics and Management Science. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511805127 - Dockner, E. and Feichtinger F. (1991) On the Optimality of Limit Cycles in Dynamic Economic Systems. Journal of Economics, 53, 31-50. http://dx.doi.org/10.1007/BF01227014
- Dockner, E. (1985) Local Stability Analysis in Optimal Control Problems with Two State Variables. In: Feichtinger, G., Ed., Optimal Control Theory and Economic Analysis, 2, North Holland, Amsterdam, 89-113.
- Kuznetsov, Y. (1997) Elements of Applied Bifurcation Theory. Springer, Berlin.
- Grass, D., Caulkins, J., Feichtinger, G., Trangler, G. and Behrens, D. (2008) Optimal Control of Nonlinear Processes. Springer, Berlin. http://dx.doi.org/10.1007/978-3-540-77647-5
- Wirl, F. (1997) Stability and Limit Cycles in One-Dimensional Dynamic Optimizations of Competitive Agents with a Market Externality. Journal of Evolutionary Economics, 7, 73-89.
http://dx.doi.org/10.1007/s001910050035 - Schafer, M. (1994) Exploitation of Natural Resources and Pollution. Some Differential Game Models. Annals of Operations Research, 54, 237-262. http://dx.doi.org/10.1007/BF02031736
Appendix
Proof of Proposition 4.1: With the specifications, given in subsection 4.2, one can compute
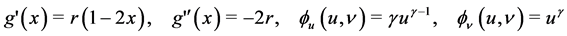
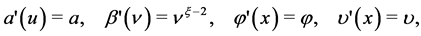
 (5.1)
(5.1)
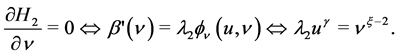 (5.2)
(5.2)
Combining (5.1) and (5.2) the optimal strategies take the following forms
 (5.3)
(5.3)
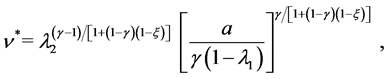 (5.4)
(5.4)
and the optimal harvesting becomes
 (5.5)
(5.5)
with the following partial derivatives
 (5.6)
(5.6)
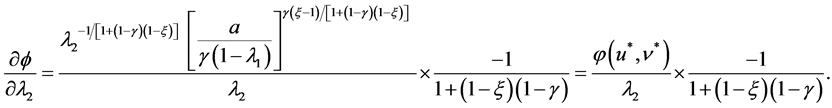 (5.7)
(5.7)
Both derivatives (5.6), (5.7) are negatives due to the assumptions on the parameters![]() ,
, 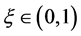 and on the signs of derivatives, that is
and on the signs of derivatives, that is ,
, 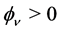 ,
, 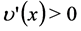 ,
, 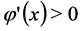 , which ensures the positive sign of the adjoints
, which ensures the positive sign of the adjoints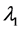 ,
,![]() . Condition
. Condition 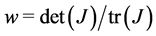 now becomes
now becomes
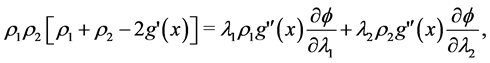
which after substituting the values from (5.6), (5.7) and making the rest of algebraic manipulations, finally yields (at the steady states)
 (5.8)
(5.8)
where we have set  stemming from the adjoint equation
stemming from the adjoint equation  , which at the steady states reduces into
, which at the steady states reduces into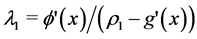 .
.
Condition ![]() after substitution the values from (5.6), (5.7) becomes
after substitution the values from (5.6), (5.7) becomes
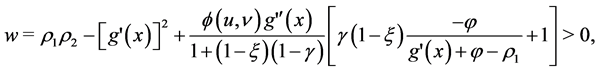 (5.9)
(5.9)
The division (5.8) by ![]() yields
yields
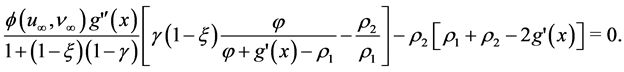 (5.10)
(5.10)
The sum (5.9) plus (5.10) must be positive, thus after simplifications and taking into account that 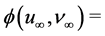
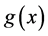 , we have:
, we have:

NOTES

1Hopf bifurcations occur when there are two pure imaginary eigenvalues of the Jacobian matrix. Hopf bifurcations, so called bifurcations of codimension one, are related to the existence of a simple real eigenvalue of Jacobian matrix equal to zero. The dynamic change produced by values of the parameter higher than the bifurcation value has the result of closed trajectories (limit cycles). The equilibrium point for which there exist any of these two types of eigenvalues is known as non hyperbolic equilibrium point.

