Modern Economy
Vol.4 No.11(2013), Article ID:39863,17 pages DOI:10.4236/me.2013.411079
Undesired Excess Capacity and Equilibrium in an Advanced Market Economy
Fondazione Ugo Bordoni Viale del Policlinico 147, Rome, Italy
Email: apannone@fub.it
Copyright © 2013 Andrea Pannone. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 26, 2013; revised August 24, 2013; accepted August 30, 2013
Keywords: undesired excess capacity; production theory; macroeconomic equilibrium; ICT; ex-post sunk cost
ABSTRACT
In this paper I attempt to give theoretical foundation to the concept of undesired excess capacity that I define as an unwilling, persistent mismatch between productive capacity and final demand. Undesired excess capacity has traditional room only in oligopolistic framework, like in Keynesian and Post-Keynesian models. Otherwise I show the possibility of its existence (and persistence) also with reference to a perfectly competitive economy where firms use massively information and communication technologies (ICT). In this stylized economy, undesired excess capacity is associated with “ex-post” sunk costs, in terms of mismatch between total revenues and production costs. My approach, which draws a production theory alternative to the neoclassical one, makes it possible to account for these costs and connect them to the role of money, under the form of credit, in the continuation of the economic process. Moreover, in the conclusion of this paper, I show how the notion of equilibrium that emerges from the analysis could be useful to address the issue of dynamics.
1. Introduction
Excess capacity, that is, actual production below the potential level, appears as a persistent feature of the modern economies. Even though there is not yet a complete consensus on how excess capacity should be defined and measured at a global level, one can clearly observe persistence of this phenomenon in many productive activities of the Western economies for at least three decades. For example in the period 1997-2009, the average rate of industrial capacity utilization of US, Europe and Japan was well below 80%1! Great recession has further emphasized the problem2 clearly, unfolding the crucial role of inadequate final demand in determining widespread production slowdown and job cuts. However, this paper does not intend to enter into the debate among economists about the validity of statistical measures of capacity (under) utilization3 but rather to give theoretical foundation to the concept of undesired excess capacity4 and to evaluate its cost for a stylized advanced economy. To reach this aim I provide a formal framework. The direct ancestor is the formalism adopted in Marini and Pannone [8] to derive a theory of capacity utilization of a firm that, independently on the specific field of activity, is characterized by the presence of information and communications technologies (in short ICT) along the entire supply chain. ICT are able to support a just in time type organization of the production process that guarantees the complete elimination (or at least a significant reduction) of resource idleness. By adopting this framework, excess capacity can be unequivocally ascribed to weak demand signals (for example low level of purchase orders or low expected sales), instead of firm-specific technical inefficiencies. Nowadays ICT are often acknowledged as “special” technologies in the sense that they affect a multitude of sectors and economic activities. Increasingly strong, although not final, empirical evidence supports the idea that ICT are able to serve as general-purpose technologies (see Kretschmer [9] for an extensive review)5. Based on these arguments, in the present paper I will extend the above capacity utilization theory to an advanced market economy6 where the bank system is assumed to entirely finance the purchase of funds (machines first of all) by firms, which re-pay year after year the debt by means of the proceeds from sales to customers. The analysis will lead me to define a non-conventional notion of competitive equilibrium compatible with the presence of undesired excess capacity. His first result is very far from the main conclusion of the economic literature on the matter. In fact market competition, by means of price flexibility, is ever viewed as being able to lead (more or less quickly) to an equilibrium with full capacity utilization, that is, to equality between demand and potential supply. For this reason the notion of undesired excess capacity had basical room in imperfect competition frameworks (monopoly or oligopoly), where there is a falling demand of checking decreasing costs7. This is true, for example, both for Keynesian (more or less bastards) and the post-Keynesian approach (see among others, Kalecky [13], Halevi and Kriesler [14], Hein et al. [15]) where excess capacity (and involuntary unemployment) is connected to the role played by effective demand, and thus investment determins the short run rate of capacity utilization. While completely agreeing with the crucial role of the actual demand, I attempt to provide a more general theoretical result. I will do this just to show that undesired excess capacity could exist (and persist) also in a perfect competition framework, although it is redesigned significantly in the light of our capacity utilization theory. Moreover, the analysis allows to derive dual cost accounting expressions that are useful to determine the total cost of the undesired excess capacity, which appears “ex-post” in the economy because total revenues are not able to recover production costs. This is the second result of the paper and it opens the door to considerations on the role of money, under the form of credit, in the continuation of the economic process.
The paper is organized as follows. In Section 2, I briefly discuss how production is (more or less explicitly) sketched in the traditional competitive framework and what this sketch implies in term of resources utilization. In Section 3, I show that recent observation of industries in advanced economies may allow to formulate new hypothesis for representation of the “productive fact”. In Section 4, I present my ICT-based capacity utilization theory. In Section 5, I extend the framework of Section 4 to a stylized market economy, define a notion of equilibrium compatible with excess capacity, and present accounting expressions that are derivable from the new production framework. Section 6 concludes the potentiality of the framework in direction of evolutionary macroeconomics.
2. Production Theory and Equilibrium in the Traditional Competitive Framework
Although the modern theory of firms and markets is based on imperfect competition, asymmetric information, transaction costs, and notwithstanding the microeconomic textbooks today devote a smaller and smaller part to perfect competition, the concept of perfectly competitive equilibrium, that expresses an ideal state of affairs that cannot actually be realized, is the benchmark from which the most part of the microeconomic analyses has been departed. In fact a very large stream of the past century academic work has been devoted to understanding what happens in the market if one or more of the simplistic assumptions characterizing the perfect competition framework do not apply8. As it is well known these assumptions are9:
1) firms produce and sell a homogeneous product to the aim to maximize profits;
2) there are a large number of small firms;
3) firms are price takers;
4) there is free market entry and exit;
5) firms and consumers have perfect information.
Moreover, another crucial assumption characterizes (more or less explicitly) the perfect competition framework. The assumption concerns the “productive fact” underlying the market trade relationships. It is generally designed as a set of input-output relations selected from an array of feasible technologies, i.e. the production function, by a process of cost minimization with respect to market-determined prices. Production function is convex and it implies absence of indivisibility10 and very high possibility of substituting the production elements at each moment and for each given scale of production. It is well known that if some kind of indivisibility is present, increasing returns exist and the production function is not convex. It implies there may not be equilibrium solutions that maximize profit at given prices (Arrow and Hahn [26], Tani [27]).
The essence of the neoclassical sketch of production can be expressed by the formula introduced by Wicksteed [28]:
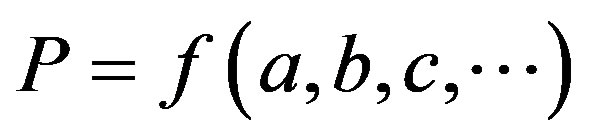 (1)
(1)
where P is the product and a,b,c,… are the factors of production.
As Georgescu-Roegen states “the prevailing silence about the nature of production was interrupted only by a few economists, who thought of providing the purely formal symbols of relation (1) with some epistemological significance” (Georgescu-Roegen [29], p. 225). Some have suggested that all symbols represent quantities of the corresponding elements; in this case, considering for the sake of simplicity only two factors of production— capital and labour—we can re-write (1):
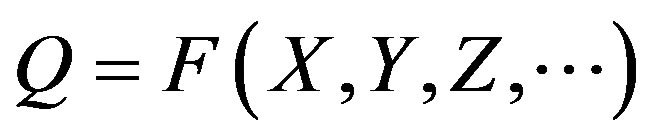 (2)
(2)
where the capital letters represent proper quantum.
The relation (2) interprets each symbol of (1) as timeless quantum. Other economists have suggested interpreting instead the symbols of (1) as flow rates with respect to time. In this case the relation (1) takes the form
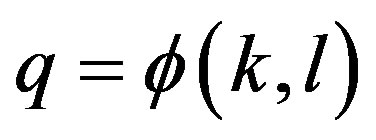 (3)
(3)
where q represents the quantity of product per time unit, t (e.g. the year), and k and l represent quantities of the services performed by the capital and labor during t. The relation (3) can be viewed as a functional, which is a function of all other functions (the inputs with respect to time). As Georgescu-Roegen pointed out (see [29]), (3) is equivalent to (2) only if all processes are indifferent to scale. In this case, the function  is homogeneous of first degree and we have:
is homogeneous of first degree and we have:
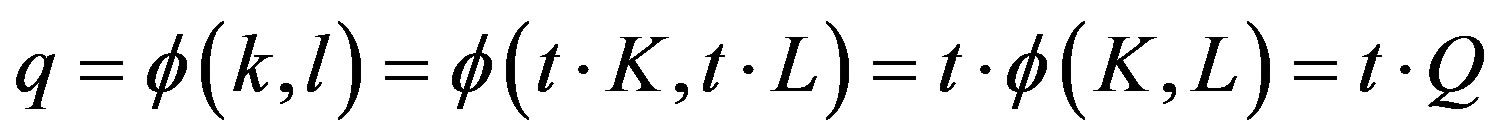 (4)
(4)
Clearly it is .
.
In other terms, the equivalence between (3) and (2) involves that q is a steady state process, which, with the convenient assumption of all-over continuity, remains always identical to itself. This means that all intensities with respect to time are constant for all elements involved and the functions-argument may therefore be replaced by the corresponding rates, that is, by numbers. “For instance the intensity of the service of ten workers is just ten workers”. In this way the functional degenerates into a simple point function (see Georgescu-Roegen [29]).
Equation (4) involves that the factors of production are continuously and completely utilized, without idleness and waste. As a result the production activity runs at maximum capacity.
However, there are many reasons why, at least in the short term, the production activity may not take place at the maximum capacity. Given the capital endowment, this can be done only by using a quantity of labour smaller than the amount of labour necessary for the maximum output rate, that is,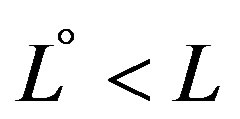 . In this case the quantity of product per time unit is given by:
. In this case the quantity of product per time unit is given by:
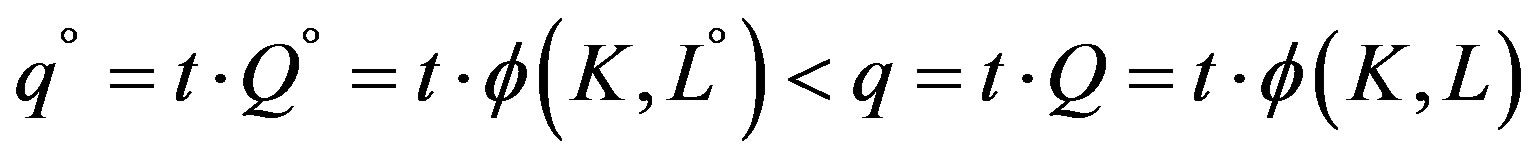 (5)
(5)
But
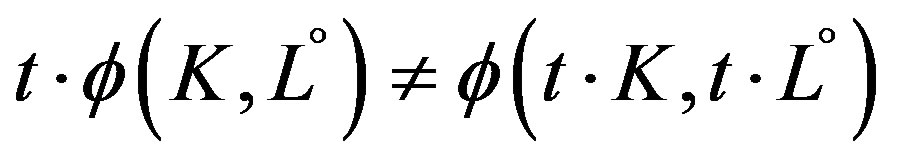 (6)
(6)
this is so because  is not a first degree homogeneous function: differently from (4), the production elements are not utilized in a continuous and complete way. In this case there is no equivalence between (2) and (3).
is not a first degree homogeneous function: differently from (4), the production elements are not utilized in a continuous and complete way. In this case there is no equivalence between (2) and (3).
Therefore, in order to be consistently interpreted, the formula (2) should always refer to production activity running at maximum capacity. As a result, price movements guarantee (more or less instantaneously)11 compatibility between output and market demand, according to a mechanism similar to the Say’s law. In other terms, in the traditional competitive framework, persistent excess capacity cannot have room. We observe that the price signal is assumed to be the only market information that is considered truly relevant to determine the equilibrium. The demand signal plays no real role.
3. New Insights from Recent Observation of Industries
Recent observation of industries could help to formulate new hypothesis for an alternative production theory. Manufacturing in advanced economies suggests that production decisions are increasingly oriented by demand signals (such as purchase orders, or expected sales). In fact empirical evidence shows as most goods and services in the nonfarm business sector of the Western economies are sold to “regular customers” with whom sellers have an ongoing relationship (see Blinder’s survey [32])12. Price adjustments are relatively infrequent and fixed price contract common13. This is also for not to disturb continuing customer relations. Unexpected price changes in the terms of implicit contracts may antagonize customers and diminish the firm’s reputation even in Internet-based selling contexts14, although these markets are very flexible and competitive. This is because with reduced search and switching costs for the consumer in e-commerce, firms may lose more of their customers when they violate consumer expectations (see Bergen et al. [38], Kauffman and Lee [39]). Moreover, Internet enables sellers to quickly monitor and react in real time to their competitors’ price cuts, and often creates an environment for firms to engage in tacit collusion (see Arbatskaya and Baye [40]). In this picture price is, at least partially, deprived of the role of exclusive point of reference for production decisions, which instead it assumes in the framework of Section 2. Consistently, one can see demand-driven production systems based on ICT, like ERP (Enterprise Resource Planning), SCM (Supply Chain Management), and MRP (Manufacturing Resource Planning), to be very common in industries like electronics, automotive, pharmaceutical, and aerospace. These systems, in virtue of superior ability to use machines in modular way and to coordinate different operative tasks, make it possible to eliminate the idle periods from the entire supply chain, reduce stockpiling and warehousing, and permit a more timely and accurate response to demand signals (see Milgrom and Roberts [41], Morroni [42], Marini and Pannone [8], Pannone [43]). In this industries production of goods does resemble production of services that arises only after the demand turns up and for that it requests high adaptability in assigning facilities. Clearly, the above industries are furthest ahead, because they either have short product lifecycles or rely on just-in-time manufacturing15. However makers of discrete goods-apparel, furniture, and other style-oriented products-as well as grocery and other mass-market retailers are even more looking at these systems. In this direction is crucial the role of Internet to accomplish the lean supply chain and facilitate the extraction of realtime data which can then be used as input to analytic models for customer behaviour (see Bruun and Mefford [44], Varian [45]).
Finally we observe that ICT, under form of computers, internet, geographical information systems, mobile phones, as well as traditional media such as radio or TV, are increasingly widespread also in the global system of agriculture that today, because population growth, globalization, and urbanization, is very much driven by the demand side. Improvements—that stem from information about pest and disease control, new varieties, new ways to optimise production and regulations for quality control—permit to enhance agricultural production and calm prices.
In conclusion, in advanced economies adoption of ICT is ever more determining a shift from a product-centered approach (characterizing, for example, the Fordist manufacturing production)—where the customer buys whatever the firm decides to produce and bring to the market—to a customer-centered approach—where the firm produces and bring to the market exactly what the customer wishes to buy and when she(he) wishes to buy.
4. An ICT-Based Capacity Utilization Theory
In the light of the above insights I propose an ICT-based capacity utilization theory where quantity signals, reflected by costumer orders and/or expected sales, play a central role in production decisions. Moreover indivisibilities and complementarities among production elements are fully integrated in the framework. A primordial version of this theory is in Marini and Pannone [8], which may be consulted. In this section I present a more compact version.
4.1. The General Assumptions
We assume that a one-stage production process provides a commodity using two production elements, “capital” and “labour”. Following Georgecu-Roegen ([29,46,47]) the production elements are thought as funds16. The concept of fund identifies an element that enters and leaves the process, providing certain services over a certain period of time. It is therefore never physically incorporated in the product17. As a result the utilization of each fund is characterized by a specific time profile, with some possible idle times.
In this picture I assume:
1) “capital” (machines) incorporates ICT software that allows to encapsulate the functionality of each unit in relatively independent modules (subunits). Each module is separately usable to perform one elementary process, that is, the production process of a unit of commodity. We call this feature of capital technical divisibility. It implies high adaptability to variation in produced quantity. However, firms cannot buy less than one unit of capital: we call this feature economic indivisibility (see Morroni [42]). On the other side worker, the unit of the fund “labour”, is characterized by both technical and economic indivisibility in that it can only be in one place at one time. Economic indivisibility of capital and labour implies no (or very low) possibility of substituting the production elements.
2) Production decisions mainly depend on the existence of a demand signals, reflected by customer orders and/or expected sales; if this signals lack or are weak then the production process does not start or production runs below the maximum capacity. Presence of ICT software permits to manage just in time the signals from the market.
4.2. The Equations
Let us assume that the observation period of production is the working year T. It is defined as product by the duration of the working day fixed by contract, expressed in hours, and the number of working days in a year.
For simplicity we assume also that the elementary process (i.e. the production process of a unit of commodity) requires no more than one subunit of capital (that is an independent module of a capital unit, see above) and one unit of labour (worker). And let  and
and 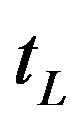 be, respectively, their absorption times in the elementary process. They refer to optimal operation conditions from an engineering point of view and are expressed as fractions of T18. Technical inefficiency, under form of idleness, could derive by the fact that a unit of capital and a worker have different absorption times and different activation scales of elementary processes. Hence a unit could be forced to wait for the other before to be re-usable. This would determine time waste. How to solve the problem?
be, respectively, their absorption times in the elementary process. They refer to optimal operation conditions from an engineering point of view and are expressed as fractions of T18. Technical inefficiency, under form of idleness, could derive by the fact that a unit of capital and a worker have different absorption times and different activation scales of elementary processes. Hence a unit could be forced to wait for the other before to be re-usable. This would determine time waste. How to solve the problem?
Posing T = 1, the minimum efficiency scale of production, that is, the minimum number of elementary processes that permits the elimination of idleness in production is given by:
 (7)
(7)
where  is the least common multiple; k is number of subunits that compose a capital unit: it corresponds by hypothesis to the number of elementary processes contemporaneously activable by that unit. In (7)
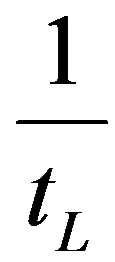
is the least common multiple; k is number of subunits that compose a capital unit: it corresponds by hypothesis to the number of elementary processes contemporaneously activable by that unit. In (7)

represents the productivity of capital, that is, the number of elementary processes activable by a capital unit during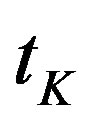 ;
;
represents the productivity of labour, that is, that is, the number of elementary processes activable by a worker during .
.
Equation (7) says that elementary processes are continuously activated without time waste. This is possible since each subunit (and then each elementary process) can be activated independently on the others and thus it can be used also if the others are already performing their task19.
We can obtain other possible efficient levels of activeity simply by multiplying (7) by a scalar (integer):
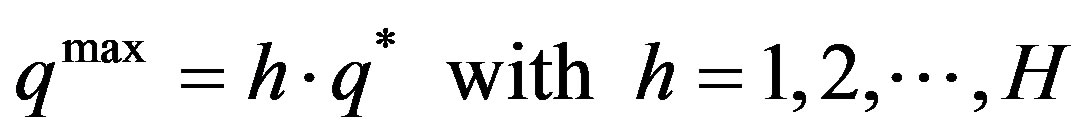 (8)
(8)
Moreover, posing for sake of simplicity h = 1, it is also true
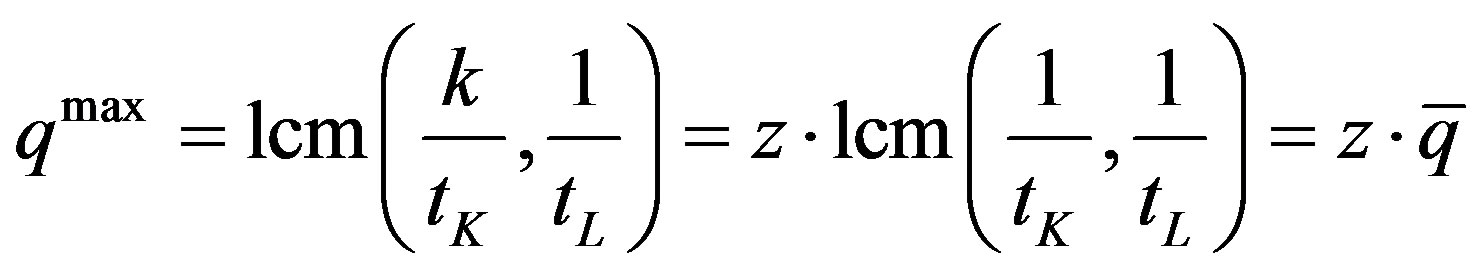 (9)
(9)
where
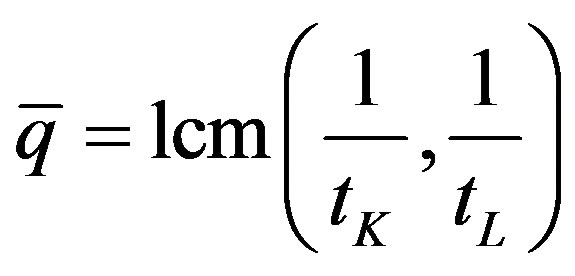
represents the minimum producible batch that defines the technical constraint to the activation of the elementary processes; z is a scalar that represents the maximum activation scale of the elementary processes according to the technological constraint20. Moreover other useful relations can be obtained:
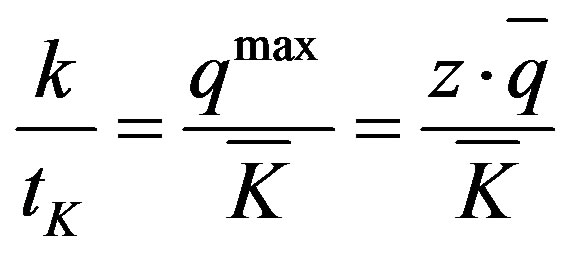 (10)
(10)
where 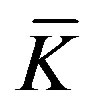 is the capital endowment, that is, the number of available units of capital. From (10) it is:
is the capital endowment, that is, the number of available units of capital. From (10) it is:
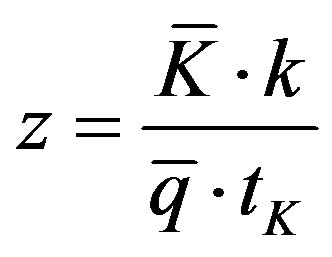 (10bis)
(10bis)
Substituting (10bis) in (9):
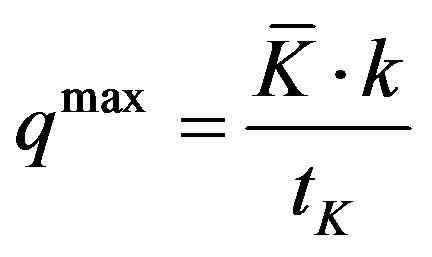 (11)
(11)
where 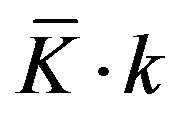 represents the number of available subunits of capital.
represents the number of available subunits of capital.
It is also true:
 (12)
(12)
where L is the workers necessary to perform production. From which we easily have:
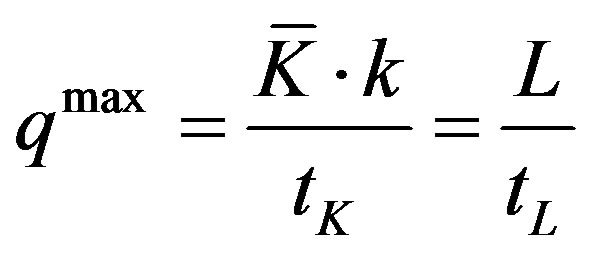 (13)
(13)
Given equations (8) and (9) we can represent all the production levels of a generic firm:
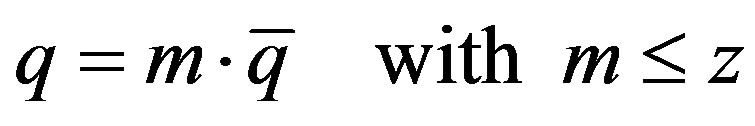 (14)
(14)
where m is a scalar that expresses the actual activation scale of the production process. We note that (14) allows to represent also levels of capacity utilization different from the maximum one.
For the sake of simplicity, in the following of our work we assume that m is a positive real number and then we consider all function of m as linear continuous functions. Clearly if the sign of equality prevails (9) is equal to (14) and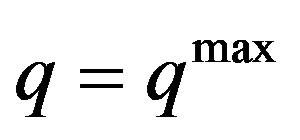 .
.
To determine the value of m we have to solve the firm’s production problem. Before of that we have to determine the firm’s production cost that consists of the expenditure incurred in the use of the funds (capital and labor).
We assume that capital units take time to be operative in production. The capital units operative at the present production period were purchased by the firm in the preceding production period and paid by recurring to bank credit. The financing covered the whole purchase value of the capital units. Current capital expenditure is assessed by means of a rental rate paid for the utilization of a capital unit within the reference production period. Such a cost is fixed by contract and it is expressed by means of a financial mathematical formula as (see Piacentini [49]):
 (15)
(15)
where 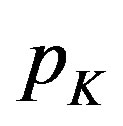 is the purchase price of a capital unit owned from the firm; r is the rate of interest relative to the reference production period and l is the technical duration of the capital.
is the purchase price of a capital unit owned from the firm; r is the rate of interest relative to the reference production period and l is the technical duration of the capital.
In case of infinite technical duration of the capital (15) becomes
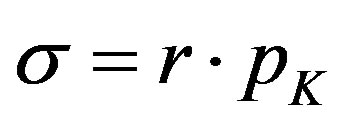 (15bis)
(15bis)
Therefore  is a cost connected to an intertemporal commitment of the firm, that is, a(n ex-ante) sunk cost.
is a cost connected to an intertemporal commitment of the firm, that is, a(n ex-ante) sunk cost.
Labour expenditure is assessed by means of the wage of a worker established by contract. At the beginning we assume that the workers amount varies to vary of the production activity. As a result labour expenditure changes in a proportional way with the production level, given fixed coefficients of use21.
The total costs of a firm can be expressed by:
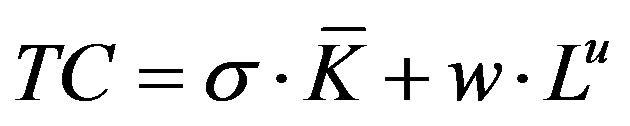 (16)
(16)
In (16) w is the annual nominal wage rate of a worker and  is the number of workers necessary to production. The latter can be expressed in the following:
is the number of workers necessary to production. The latter can be expressed in the following:
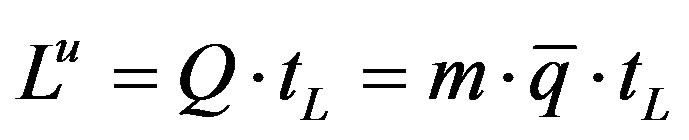 (17)
(17)
equation (17) says that the number of workers necessary to production depends exclusively on the actual activation scale of the elementary processes, given the labour productivity. Substituting in (16):
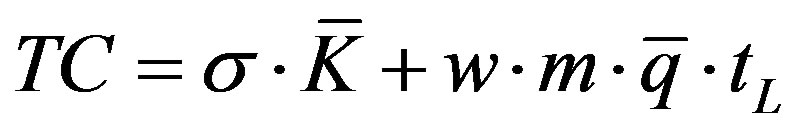 (16bis)
(16bis)
where we assume that
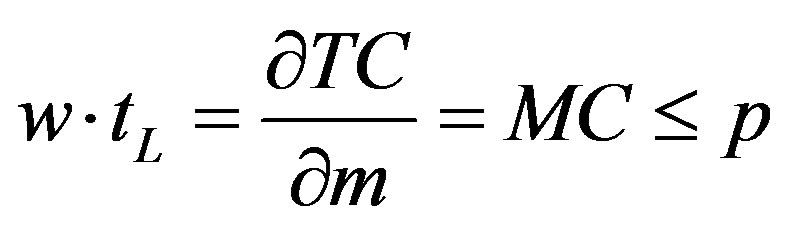
and p is the price of commodity.
In the light of (16bis) the production problem of the firm is:
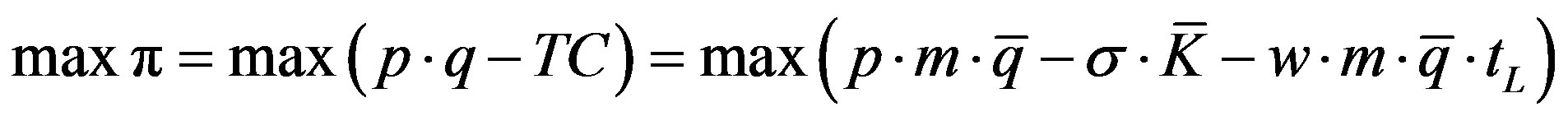
(18)
where we assume p as a given.
The constraints of the problem (18) are
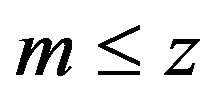 (18a)
(18a)
and
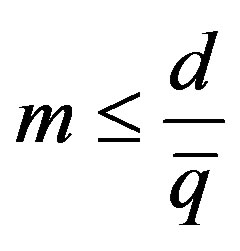 (18b)
(18b)
where d are the customer orders of the firm. The mean of (18b) should be clear: the actual production flow of a firm cannot overcome its customer orders. The sign of parity in (18b) implies that the firm is satisfying completely its orders22.
The solution of (18) is:
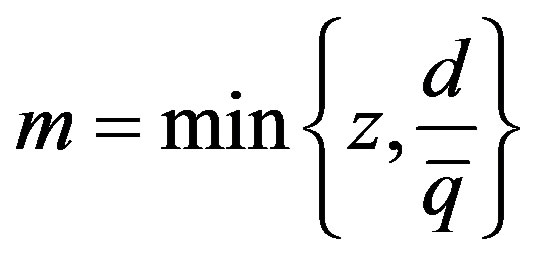 (19)
(19)
In other term the solution of (18) is the minimum between the output capacity of the firm and the amount requested for its product; (19) says that profit maximization in may imply underutilization of the firm’s capital endowment. This happens when the demand level (purchase orders) is not sufficiently high respect to the capacity output.
We note that since in our model the marginal cost is constant and equal to the average variable cost, the short period supply curve of the firm is horizontal up to the limit of the available production capacity,  , at a price equal to marginal cost
, at a price equal to marginal cost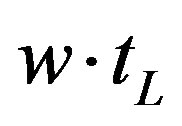 , and then it becomes vertical.
, and then it becomes vertical.
Finally we can define excess capacity of firm:
 (20)
(20)
We observe that excess capacity is unequivocally attributable to low level of purchase orders (see (19). We observe that this kind of excess capacity is “undesired” since it occurs despite the optimum choice of the firm. Moreover, we can see that (20) implies underutilization of capital. In fact from (10bis) it is:
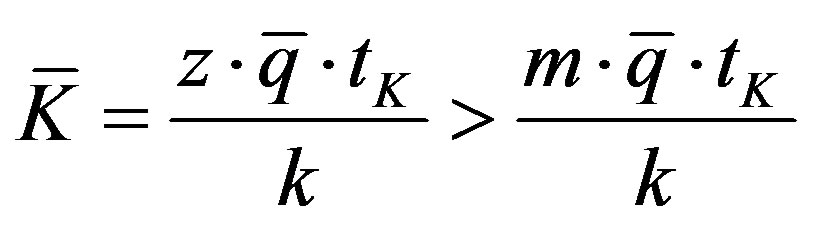 (21)
(21)
where
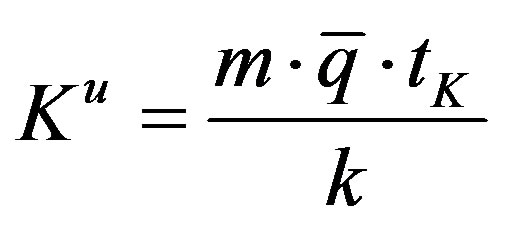 (22)
(22)
represents the number of capital units actually used. This number is rounded off to the nearest higher integer.
From (21) and (22) we can obtain a measure of capital underutilization and then, taking into account (20), the relation between capital underutilization and excess capacity:
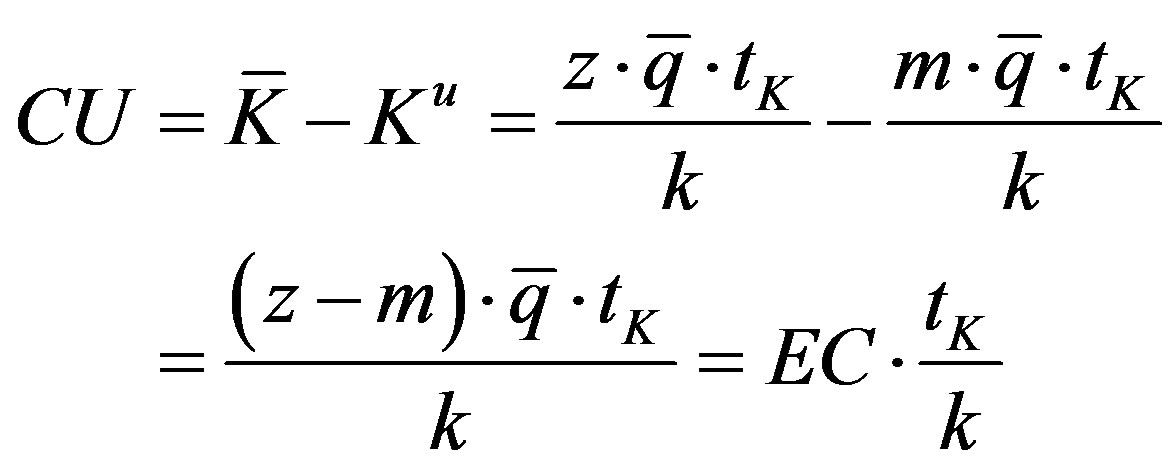 (23)
(23)
Finally, we could extend the capacity utilization model to the case of multi-production, assuming that it is possible to produce N commodities using s funds: s − 1 items of capital, and labour. Some (but not all of the) items of capital are shareable (common funds) in the sense that they are able to perform the same or different stages of different production processes with specific usage time. Hence, because of technical divisibility of the capital goods now it is possible to use up the potentialities of the shareable funds to activate jointly different types of elementary processes. We note that by means of the absorption coefficients of the funds in the different processes,
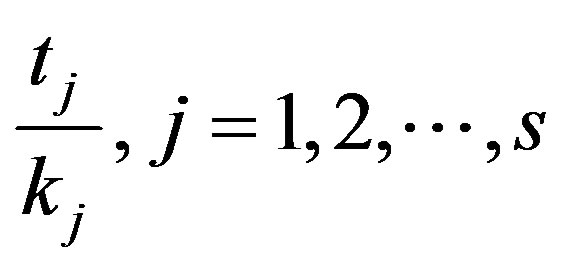 we can identify the quotas of the shareable (and of the no shareable) items of capital which are actually utilized from each product (see (22)). This is so because, compared with the traditional technical coefficient, the absorption coefficients give additional information regarding the effective utilization time of the requested amount of each fund in the elementary process.
we can identify the quotas of the shareable (and of the no shareable) items of capital which are actually utilized from each product (see (22)). This is so because, compared with the traditional technical coefficient, the absorption coefficients give additional information regarding the effective utilization time of the requested amount of each fund in the elementary process.
In this case the production problem of a firm can be represented as a typical problem of linear programming: it consists in determining the set of activation scales of the productions capable of maximizing the profit. The constraints are the same of the case of the single product, but now they refer to the level of demand of each commodity and the endowment of each fund type23.
5. Capacity Utilization and Macroeconomic Equilibrium
In this section I extend the above framework to a stylized market economy. I refer to a closed economy that produces only one commodity in steady state with no inflation, where all firms use ICT, and therefore they use the productive capacity according to the model presented in Section 4. The working of the whole economy is viewed as a circular sequence of actions that involves three kinds of agents: banks, which lend the money to firms to purchase capital and pay wages; firms, which borrowing money and take production decisions; customers, that is, workers and firms, which make the money back, respectively, under the form of expenditures for consumption and investment24. During the production period (working year) firms sell the output to customers (to workers, as consumption goods, and to firms, as investment goods25). With the proceeds of the sales, at the end of the production period, firms pay to the banking system the rental cost of capital (see Equation (15) and (15bis)) as well as they reimburse the money anticipated for wages. For sake of simplicity, we assume that money for wages is credited by banks at zero interest rate; this is because firms can re-pay money for wages completely, in the same production period. Indeed, in Section 4 we assumed that 1) firms employ workers only after receiving demand signals; 2) the commodity price major than or equal to the variable cost (labour cost).
5.1. Microfoundation
To generalize our conclusion we try to stay as close as possible to the spirit of competitive economics. Necessarily, some of the assumptions of the traditional competitive setting have to be revised just in the light of our production theory. The first problem consists of trying to reconcile the presence of ICT, which could imply some type of product customization (see Section 3), with the familiar assumption of homogeneous firms that characterizes the traditional competitive framework (see assumption suba) in Section 2).
In general terms “customization of the product” involves adding features to the product that the customers value. Customization by means of ICT could range from simple “adaptation” of delivered product by customers themselves, up to the total customization of production sale, design, fabrication, assembly and delivery (see Al-Shammari [54]). Therefore, as not to betray too much the firm homogeneity assumption, we limit to set the customization process of the product as a sort of cosmetic customization (see Gilmore and Pine [55], Al-Shammari [54]) where a standard product is presented differently to different customers. The cosmetic approach is appropriate when customers use a product the same way and differ only in how they want it presented. Rather than being customized or customizable, the standard offering is packaged specially for each customer. For example, the product may be displayed differently, its attributes and benefits advertised in different ways, or the customer’s name may be placed on each item (see Gilmore and Pine [55])26. This approach may help us to reconcile the idea of customization with the hypothesis of competitive market that asks for firms substantially identical. Along this direction we resort to the idea that the global market is divided up in as many virtual micro-markets as there are firms, n. The single virtual micro-market is composed only by the customers of the individual firm. They are the fraction of the global market consumers that addresses the orders to it. In other terms, a generic consumer of the global market becomes a customer of a given firm only after sending the order to it. The customization activity starts after the orders and ends with the phase of sales. Since the firms of the market produce a standardized physical product, we can admit that the total orders of customer are distributed fairly among them. Hence is
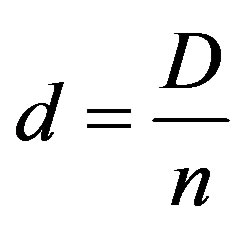 where D are the total orders that we assume to be, for sake of simplicity, an decreasing linear function of the price27.
where D are the total orders that we assume to be, for sake of simplicity, an decreasing linear function of the price27.
Our second problem concerns the price taking assumption. Also I assume that the market price is given for the single firm. However, my interpretation of the price taker behaviour of a firm is a bit different from the traditional perfect competition model. First we assume that the single firm produce at capacity. In this case, clearly, firm has no convenience to low the price; on another hand if it increases the price the others would follow it. As a result new firms would enter into the market, attracted by higher profits. This would increase the number of firms on the market lowering the level of orders for each of them (less total orders for more firms). At the limit of this process the orders of each firm would tend to zero bringing the system to the point of collapse. As a result no firm has any convenience to increase the price.
After this, let us analyze the price behaviour if firm underutilizes capacity. Given the assumption of symmetric orders, also the other firms are underutilizing their capacity. If a firm tries to low the price to increase the flow of orders that accrues to it (that is, its virtual micro-market) by spiriting it away from (the virtual micro-markets of) its competitors, they will conform instantaneously to its decision thwarting its action. As a result a firm has no convenience to lower the price. On another hand, if a firm tries to rise the price to increase the selling value then the competitors could attract its customers and increase (reduce) the (under) utilization of their capacity by holding their prices unchanged. In this condition, a firm has no incentive to increase the price.
In this second case, as well as in the case of full utilization of capacity described above, we want to underlie the conjectural nature of our argument. Indeed the actual demand (orders) of the single firm, d, that is perfectly flat (since the single firm has no power on the price), is different from as it is represented in its choice set. The latter is elastic for price increases and rigid for price decreases. To such a conjectural (and not actual) demand, it corresponds a discontinuous conjectural marginal revenue function that produces a wide range of unresponsiveness —for what concerns price decision—to changes in capacity utilization. We observe that this point of view reverberates, in some way, the sound of the “kinked demand” frame (see Hall and Hitch [57], Sweezy [58]), originally aimed at explaining the rigidity of price in imperfectly competitive markets. The opportunity to transpose the conjectural aspects of this frame into our competitive setting depends on the fact that we subdivide the global market in virtually distinct markets even though equal in size, product and price (see above). As an effect firms may experience some form of competitive interaction since each of them must take care of its rivals behaviour. For this reason a single firm is deterred from undercutting or raising price by the knowledge (or by the belief of knowing) that its competitors can respond. Under this light, the kinked demand frame may be thought of as a theory about how tacit collusion works can work in an environment with an unlimited numbers of homogeneous firms, perfect information and free entry, instead of a theory of price rigidity in an oligopolistic market. In conclusion, according to the adopted perspective, the actual marginal revenue has no more direct relevance for the firm unless very large excess capacity occurs. Given the price, firm maximizes profits simply determining the quantities in response to customer orders. However, as we will see at the end of Section 5.3, the price behaviour could change in presence of a very large fall in the global demand that brings the economy to the point of collapse.
Our last problem concerns the assumption of absence of barriers to entry. How this assumption could be reconciled with our framework, which implies the presence of intertemporal commitments associated to the cost of capital (ex-ante sunk cost, see above Section 4 Equations (15) and (15bis))? The strategy literature on commitment has recently argued that irreversible actions like investments can influence the play of other actors in way beneficial to players able to commit (see Besanko et al. [59], cap. 7). Along this line, the model of two stage game of Cabral and Ross [60] shows as the sunkness of entry costs can rend unprofitable the incumbent’s predation strategy and allow to the entrant to stay in the market.
If an entrant, who would otherwise anticipate an aggressive response by the incumbent (in an effort to chase the entrant from the market), can commit itself irreversibly to that entry, it can defeat the purpose of the incumbent’s retaliation. In this view, high levels of sunk investment may actually facilitate entry if they serve to commit entrants to staying in the market and thereby induce the incumbent to adopt a more accommodating strategy (see Cabral and Ross [60], p. 99).
Coming back to our competitive framework we assume that firms are small and have identical technology. Hence, both entrant and incumbent firms face the same sunk costs, which are evaluated as “high enough” by each entrant since higher sunk costs do not exist. As we saw, these sunk costs can serve to commit entrants to staying in the market. In this case incumbent firms fail to prevent entry strategies. In sum, along this perspective, the existence of sunk costs is not in contrast to the assumption of absence of barriers to entry that our competitive framework calls for.
5.2. The Aggregate Supply Curve
Referring to equation (14) in Section 4.2, we can express the aggregate production level as:
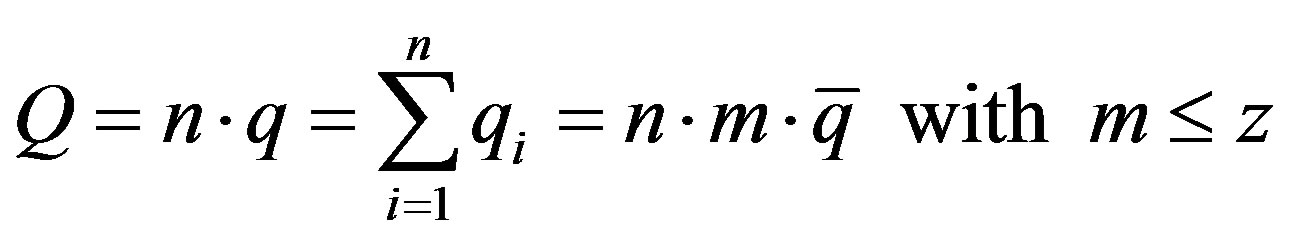 (24)
(24)
In the same way, also the other relations described in that section could be extended at aggregate level. However, with reference to the production problem in (18), another constraint should be added to (18a) and (18b):
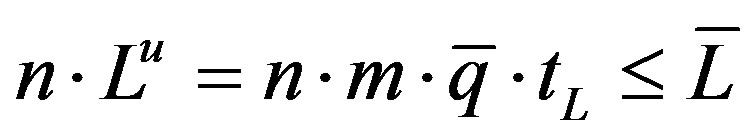 (25)
(25)
where 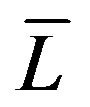 is the labour supply that we assume to be given. Equation (25) means that the demand for labour of all the firms is constrained by the labour supply. The sign of equality implies that the economy is utilizing all the available labour28. Hence in our model, as a well in Keynes (see Keynes [56], p. 260), the volume of employment is essentially determined by the effective demand. Therefore, wage flexibility does not need if unemployment exists the labour market does not clear. We observe that our conclusion would be compatible with whatever wage setting model since nominal and real wage have no direct effect on the demand for labour and hence on the employment.
is the labour supply that we assume to be given. Equation (25) means that the demand for labour of all the firms is constrained by the labour supply. The sign of equality implies that the economy is utilizing all the available labour28. Hence in our model, as a well in Keynes (see Keynes [56], p. 260), the volume of employment is essentially determined by the effective demand. Therefore, wage flexibility does not need if unemployment exists the labour market does not clear. We observe that our conclusion would be compatible with whatever wage setting model since nominal and real wage have no direct effect on the demand for labour and hence on the employment.
In sum the supply curve of the market (that is the sum of the supply curves of all firms) is horizontal up to the limit of the available production capacity, 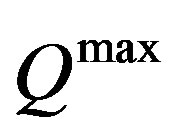 , at a price equal to marginal and then it becomes vertical (see figure 1).
, at a price equal to marginal and then it becomes vertical (see figure 1).
This involves that, up to the limit of the overall capacity of the system, the level of demand is ever equal to the level of production and hence it has no effect on the price.
However, beyond the limit of the overall capacity of the market, the price of the commodity grows in proportion to the excess of demand over the level of maximum potential production, like in a market à la Walras.
5.3. The Equilibrium
How is the market price determined?
First we assume that the total productive capacity of the economy, 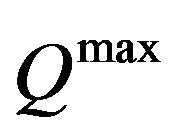 , matches perfectly the aggregate demand D (see figure 1). In the intersection point it is
, matches perfectly the aggregate demand D (see figure 1). In the intersection point it is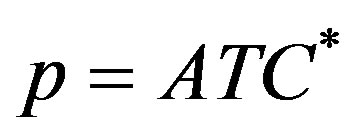 where, remembering (16bis) and (11),
where, remembering (16bis) and (11),
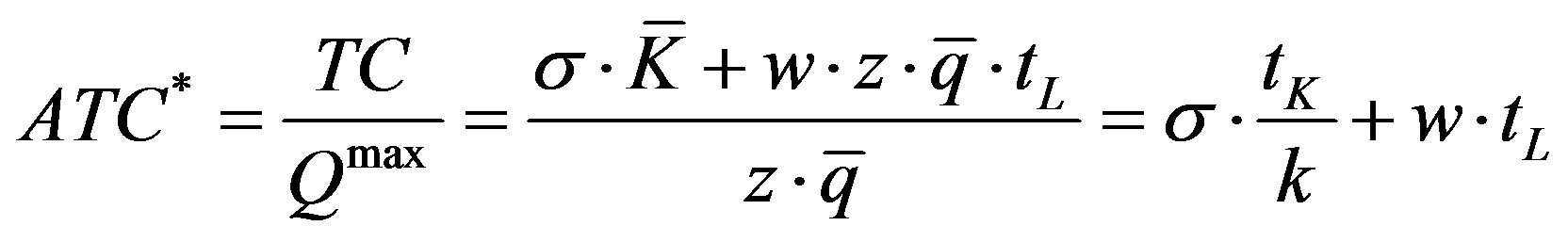 (26)
(26)
is the minimum unitary cost; in (26), for simplicity of notation, we posed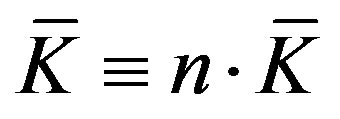 29.
29.
In fact if 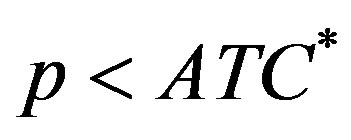 market demand would exceed the potential production and the price would increase till to match
market demand would exceed the potential production and the price would increase till to match . If
. If 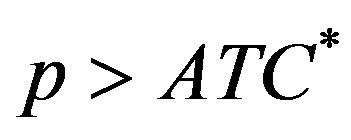 market demand would drop below the potential production and the actual pro
market demand would drop below the potential production and the actual pro
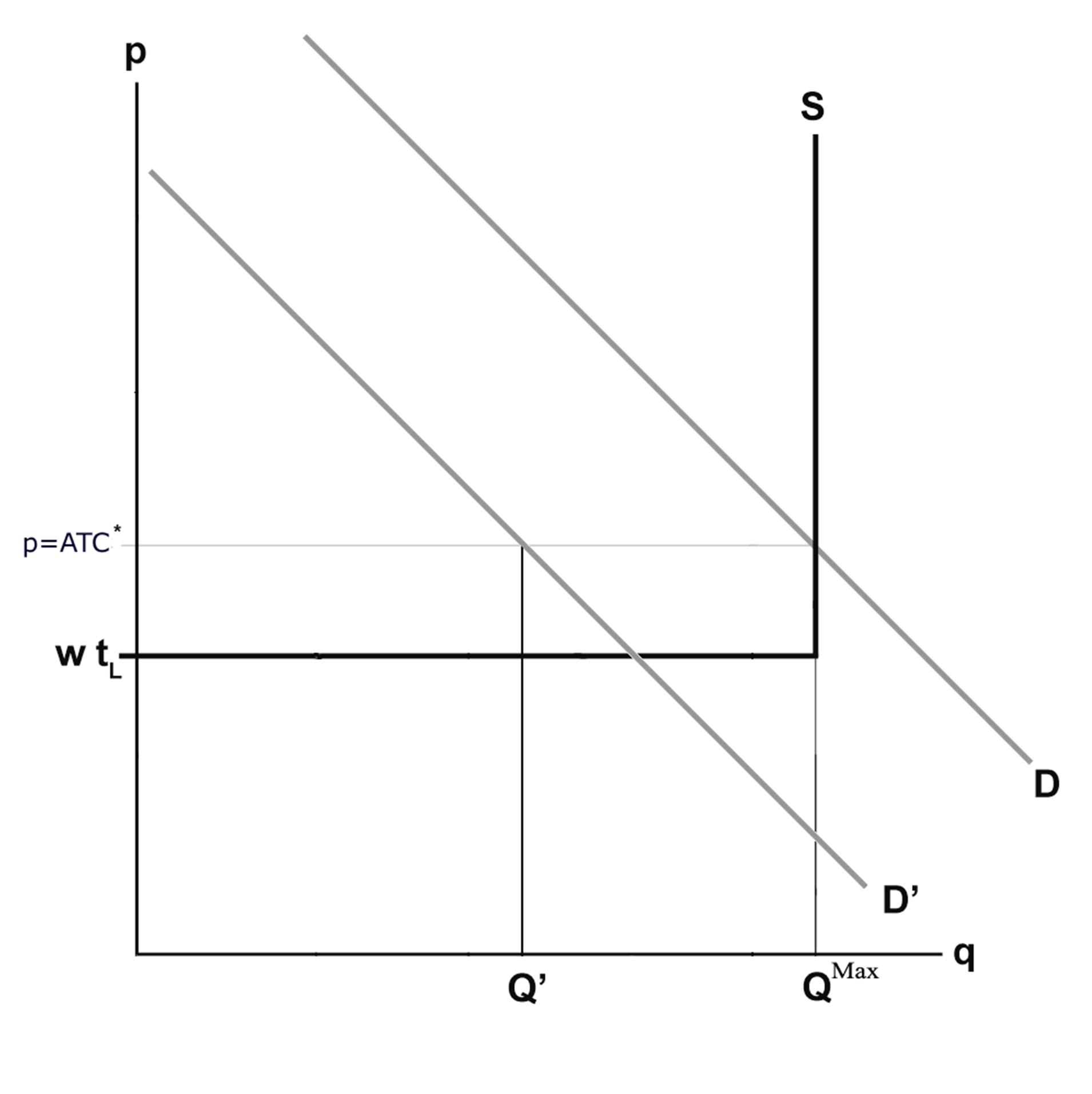
Figure 1. The macroeconomic equilibrium.
duction would be lower than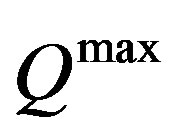 .
.
Now we assume that, starting from the equilibrium point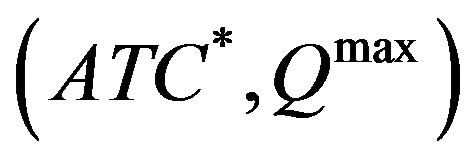 , the demand level falls under capacity as an effect of an exogenous shock (demand schedule moves toward
, the demand level falls under capacity as an effect of an exogenous shock (demand schedule moves toward 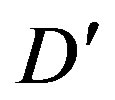 in figure 1). Since firms produce on orders (see Section 4), each firm should reduce the level of utilization of capacity and capital proportionally to the fall of the total orders, without changing the price (see above). Clearly, the point
in figure 1). Since firms produce on orders (see Section 4), each firm should reduce the level of utilization of capacity and capital proportionally to the fall of the total orders, without changing the price (see above). Clearly, the point 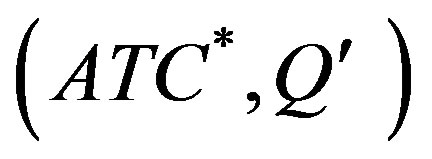 in figure 1 represents the new equilibrium of the economy. In this point there is excess capacity and unemployment, because firms do not use the whole labour supply. As a result the actual unitary cost, that I will indicate by ATC (see Section 5.4), is greater than the minimum one, and hence the price. Therefore in the new equilibrium point each firm incur losses. Despite it firms, at least in the short period, continue to stay on the market because of their intertemporal commitments (see Section 5.1). The way to survive will be analysed in Section 5.4 and even further in Section 6.
in figure 1 represents the new equilibrium of the economy. In this point there is excess capacity and unemployment, because firms do not use the whole labour supply. As a result the actual unitary cost, that I will indicate by ATC (see Section 5.4), is greater than the minimum one, and hence the price. Therefore in the new equilibrium point each firm incur losses. Despite it firms, at least in the short period, continue to stay on the market because of their intertemporal commitments (see Section 5.1). The way to survive will be analysed in Section 5.4 and even further in Section 6.
We observe that the notion of “equilibrium with excess capacity” implied by our analysis is very different from the disequilibrium notion that occurs because “something” (for instance price rigidity) hampers production to be sold. Instead we intend equilibrium with excess capacity as a status in which potential production is different from the actual demand. Therefore this notion refers to a disharmony between stock and flows rather than between flows. In fact within this benchmark there is always equality between supply and demand on the commodity market. Firms fit the incoming demand but do not use all their available capacity. Excess capacity (and capital) cannot be eliminated from the price flexibility since rational firms have not convenience to move the price.
However the price behaviour could change in presence of a very large fall in the global demand that determines a wide involuntary unemployment and, in turn, a generalized reduction of money wage30 and minimum average cost (see equation (26)). In this case price would adjust to match the new lower level of . As a result we have:
. As a result we have:
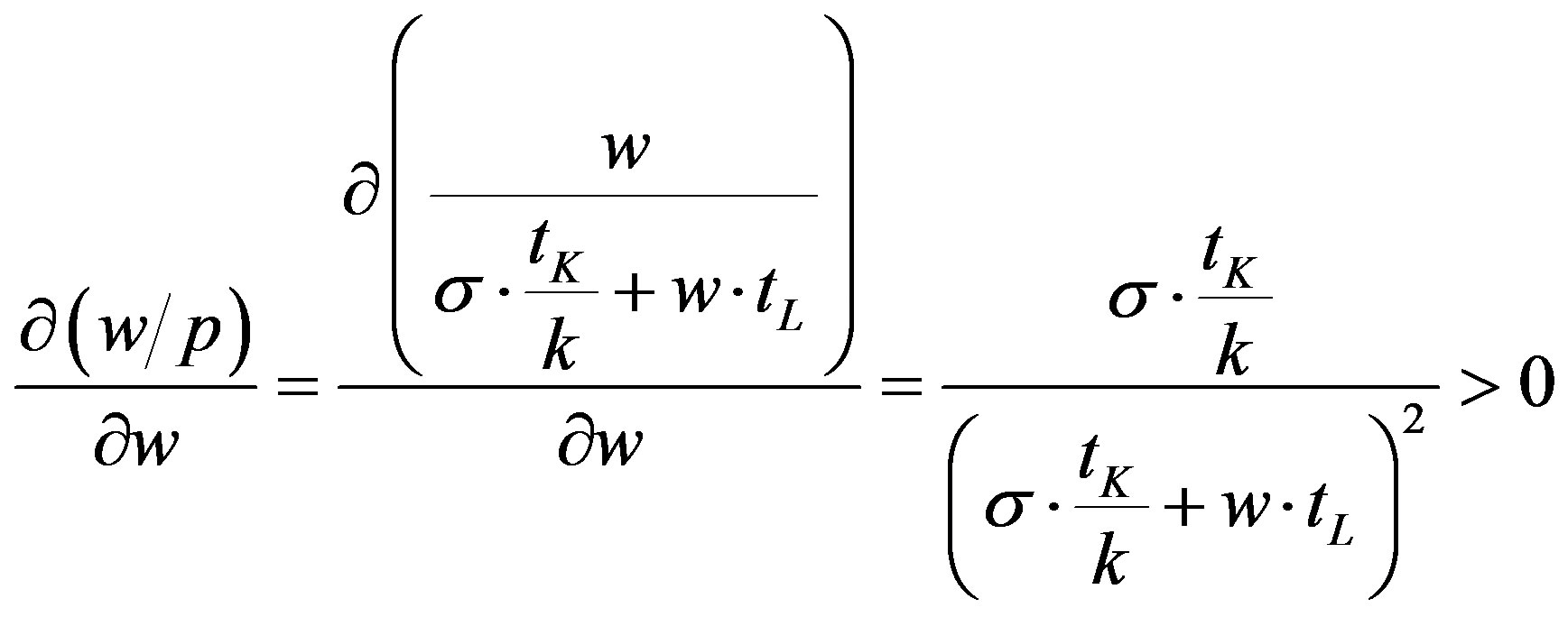 (27)
(27)
The sign of derivative says that the real wage decreases as money wage and price decrease. In other terms, price decreases less than proportionally to wage. It depends on the structure of costs that incorporates the total rental cost of capital.
While the decrease of real wage has no direct effect on the demand for labour (see equation (17)), it may determine
• a slump in workers’ expenditure and in the global demand (demand schedule in figure 1 moves toward left)31;
• a further reduction in the output and unemployment;
• a larger increase in the actual average cost.
In this context firms could break the collusive interaction and give rise to a price war.
“Price collusion is more difficult to be sustained in declining markets, where tomorrow’s profits (with or without retaliation) will be small anyway—in the limiting case where the market is on the verge of collapsing, there is almost no ‘future’ and therefore no possibility to induce firms to stick to a collusive conduct” (see Ivaldi et al. [62], p. 27).
This war could push the price well below the average minimum cost and also much lower than the average effective cost of the firms. At this time it is clear that a sizeable restructuring of the market will involve losses, dead and blessed. The extreme limit of this process is a situation of monopoly or of oligopolistic trust that globally determines the price, confronting to the whole demand schedule. For a more accurate description of this process see Marini and Pannone [8]. In this case the equilibrium price would be:
 (28)
(28)
where 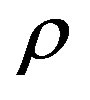 is an “desired” profit rate that we define as a profit rate that guarantees revenues greater than costs. We note that equation (28) recalls the “full cost principle” (see Hall and Hitch [57]) as re-formulated by Sylos Labini ([4], p. 93). More precisely (28) looks at the Sylos formula:
is an “desired” profit rate that we define as a profit rate that guarantees revenues greater than costs. We note that equation (28) recalls the “full cost principle” (see Hall and Hitch [57]) as re-formulated by Sylos Labini ([4], p. 93). More precisely (28) looks at the Sylos formula:
 (29)
(29)
where
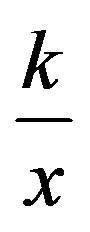
are the unit fixed costs, x the normal level of utilization of productive capacity32, v the variable costs and s is the minimum profit rate, instead of the equivalent wellknown Sylos’ formula:
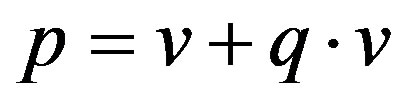 (30)
(30)
where q is the mark-up on variable costs, adopted by Modigliani and other neo-Keynesian authors33.
In this new context, a fall of total demand that determines undesired excess capacity and increase of actual average cost could be:
• ignored by leader firms since revenues greater the minimum average cost cover the higher average cost;
• countered by leader firms with a price reduction (and hence a reduction of the desired profit rate) till to restore equilibrium.
These considerations lead us to formulate a more general expression of the equilibrium price valid for all setting (perfect competition and monopoly/oligopoly), as well as, for each utilization level of capacity (maximum and below the maximum)
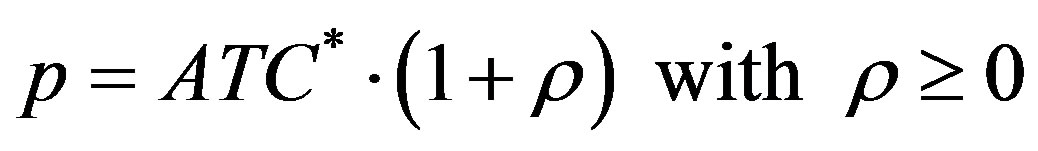 (31)
(31)
Clearly 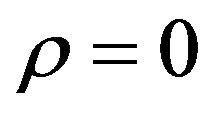 in perfect competition while
in perfect competition while 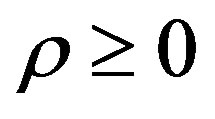 in monopoly/oligopoly34.
in monopoly/oligopoly34.
5.4. Undesired Excess Capacity and “Ex-Post” Sunk Cost
The competitive equilibrium with undesired capacity showed in figure 1 implies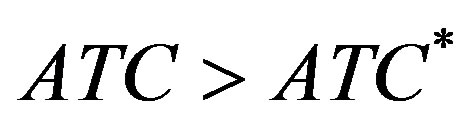 . In fact from (16bis) we know that a fixed side and a variable side compose total cost and hence the unitary cost will decrease (increase) when the production flow increases (decreases).
. In fact from (16bis) we know that a fixed side and a variable side compose total cost and hence the unitary cost will decrease (increase) when the production flow increases (decreases).
To determine the formula of ATC we refer to (11) from which, by means of easy transformation, we can obtain:
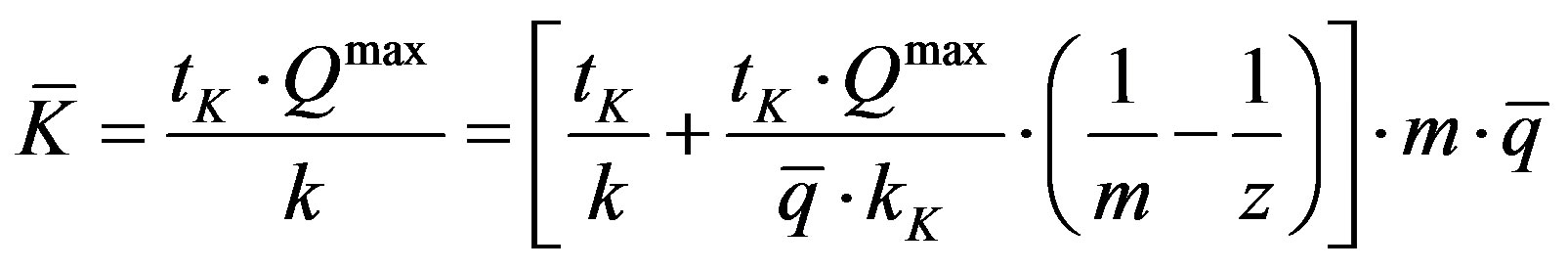 (32)
(32)
Substituting (27) in (16bis) and dividing by Q (production below capacity) it is:
 (33)
(33)
In (33) the component
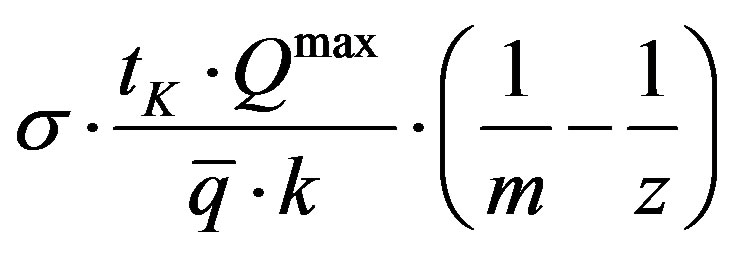 and hence ATC, varies inversely to vary of the activation scale till to the limit of capacity. Clearly at the limit of capacity it is
and hence ATC, varies inversely to vary of the activation scale till to the limit of capacity. Clearly at the limit of capacity it is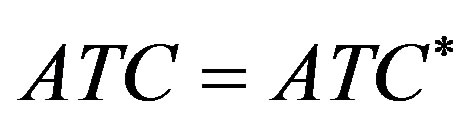 . That is a form of short-run returns to the operation of the capital, not returns to scale and not increasing marginal productivity. This means that, in our framework, average decreasing cost and constant marginal cost (see above) are compatible with a competitive setting.
. That is a form of short-run returns to the operation of the capital, not returns to scale and not increasing marginal productivity. This means that, in our framework, average decreasing cost and constant marginal cost (see above) are compatible with a competitive setting.
We observe that,
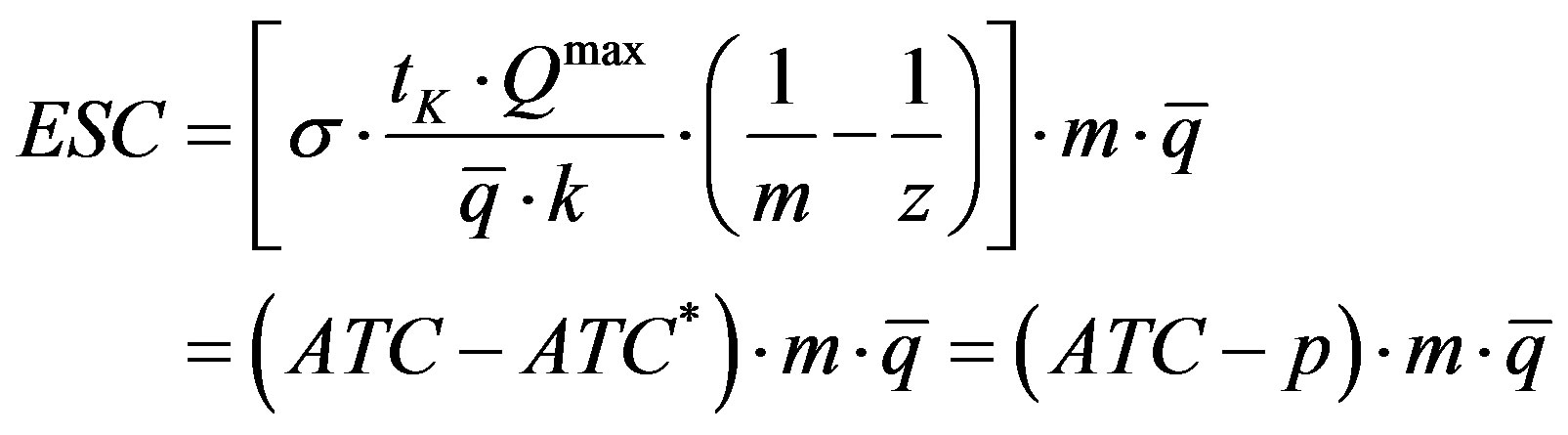 (34)
(34)
is the “ex-post” sunk cost associated to the presence of excess capacity in the economy. It derives from the fact that the total revenue from sales does not cover the total production cost. Moreover, remembering (23), it is also
 (35)
(35)
In other terms, in our perfectly competitive setting the ex-post sunk cost coincides with the total cost of the unused capital35. From (23) it is also:
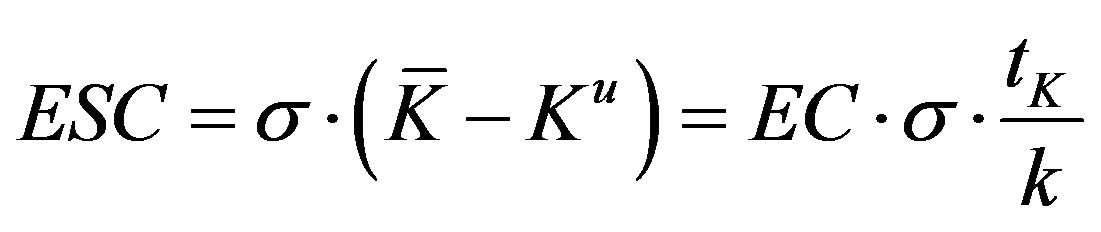 (36)
(36)
where from (26) we know that
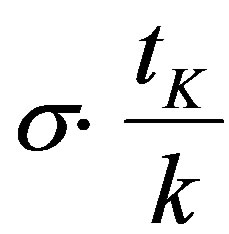
is the minimum cost of a capital unit.
We observe that the ex-post sunk cost can be accounted just because we think the production elements (machines first of all) as funds and evaluate them by means of the rental rate paid for their utilization. The very nature of funds, which must be in the availability of the manager of the production process, but whose intensity of application may differ according to the continuity of their use, imply that unit costs depend crucially on the “saturation” of a potential productivity over the production period (see Piacentini [49]), while the cash flow required for their availability has to be however paid at the beginning of the production period. We observe that to account undesired excess capacity would not be possible adopting the more traditional notions of input and opportunity cost. This is so because the opportunity cost of excess resources that have no alternative use would be zero.
In presence of ex-post sunk cost, money, under form of new credit, is called to play a crucial role for the continuation of the economic process. This is so because ex-post sunk cost implies, at a systemic level, non consistency between initial finance, that is the credit-money necessary to start the production process of firms, and final finance, that is the liquidity flows that come back to them in the form of expenditures of wage-earners and firms (investment). In other terms firms are not able to refund, at the end of the production period, their debt with the banking system, which financed the capital purchases in the preceding production period (see Section 4.2)36. To reimburse the credit loan, so closing the monetary circuit, several possibilities are opened: for example one could assume that a firm uses own assets and liabilities to generate the necessary cash flow. Another possibility is that the firms get all the funds by issuing securities—that are bought by workers that (if any) have active cash balances—and use this money for reimbursing the banks. Lenders obtain a security interest in the property of the firms as stipulated by a contract. Any asset acceptable to the lenders can secure general loans. Mixed solutions between internal and external cash flow are the rule in the real world. In other terms money permits firms to continue to stay in the game rather than leaving, in this way ensuring the sustainability of the equilibrium with undesired excess capacity. Clearly, remain valid the considerations made at the end of Section 5.3 about the consequence of a large fall in global demand.
6. Concluding Remarks: Toward Evolutionary Macroeconomics
The notion of equilibrium with undesired excess capacity (and capital), as it emerges from the analysis of this paper, may have a paramount importance to tackle dynamic issues. Because excess capacity, if any, could establish an indissoluble link between successive time periods contributing to re-orient the firms’ expectations and their investment decisions, it is essential, from the analytical point of view, to outline a sequential process of change (see Amendola and Gaffard [66], p. 45). In fact, since excess capacity is not eliminable by the market price mechanism, possible ex post sunk costs are transferred from period to period in absence of a change in the firms’ investment behaviour. However, at a given period the purchase of securities issued by firms to cover the ex-post sunk cost (see Section 5.4) could fall and the cash necessary to finance the credit loan could be rationed. In fact over time holders of illiquid assets could attempt to sell them in return for liquidity. This is particularly true when a risk adversion phase substitutes an euphoria phase on the assets market (see Minsky [67]). In this case firms, in order to avoid the bankruptcy, may be compelled to revise their investment routine in advance to eliminate the capacity distortion. Since investment decisions are taken on expectation of demand, it implies to revise the expectation model correcting the expected value of the final demand, whatever determined, in the light of the current capital excess. Clearly, capital excess, and then not-fulfil expectations, for one or more periods are not necessary to imply a change in the way by which these expectations are formed (see Lindhal [68], Hahn [69]). However, if nonfulfilment persisting firms have to change both expectation model and investment behaviour since they realize that the existing productive option does not fit well as in the past the needs of customers. In this context, two kinds of reaction could be imagined to correct undesired excess capacity:
1) firms slow down the pace of investment so to harmonize again the rate of increases in capacity and the expansion rate of the final demand. However, in this case the business cycle would undergo one or more periods of contraction/recession during which new unbalances and sizable market restructuration could occur (see end of Section 5.3).
2) firms use internal and/or external cash (if any) in part for reimbursing the central bank and in part for undertaking an innovative strategy. For instance, firms could create new lines of activity/products/sectors by building new specific capital goods that establish new types of complementarity with the existing capital. The introduction of new productive options could stimulate new types of demand that are able to exploit the existent capacity excess till to saturation (see Penrose [70], Teece [71]). Moreover, new commodities could also arise from the fact that firms gradually learn to use “re-combining” excess capital and human capital in new ways in order to generate new knowledge (see Weitzman [72], Antonelli et al. [73]); this is also due to the possible contribution of knowledge external to the firms (universities, public research, etc.). For example, many of the rapid innovations on the Internet (web browsers, search engines, peer to peer music files exchange, social networks, etc.) arise from the fact that
“… component parts were all bits. They were programming languages, protocols, standards, software libraries, productivity tools and the like. There was no time to manufacture, no inventory management, and no shipping delay. You never run out of HTML, just like you never run out of email. New tools could be sent around the world in seconds and innovators could combine and recombine these bits to create new web applications” (Varian [45], p. 2).
However, wide-spread innovation could trigger a sequence of new unexpected unbalances. As you can see, for example, the increasing diffusion of ICT in the US economy, if on the one hand has determined a progressive growth of productivity and productive capacity (see Brynjolfsson and Saunders [74]), on the other hand it has also led to business-process reorganization involving a wide expansion of the flexible working practice. In particular, temporary employments, outsourcing of non-core functions previously handled in-house (Espino-Rodriguez and Padron-Robaina, [75], Farrell, [76]) and the inter-related development of the phenomenon of globalization of production, have weakened the bargaining power of the trade unions and altered the balance of power between firms and workers, with a consequent pressure on real wage and huge redistributive effects37. In this scenario, inevitably, even high-skilled workers have not been preserved from the reduction of the purchasing power38. As a result, in the period 1997-2006, the distribution of income in US started to shift systematically in favour of the richest quintile of the population and the final demand growth rate has progressively lost pace. The further effects have two. On the one hand“the incomes accruing to all those taking advantage of the redistribution go then to finance the purchases of already existing stocks of wealth, strongly inflating their monetary values given the small percentage of these stocks actually put on the market” (Amendola and Gaffard [78], p. 21).
On the other hand the necessity to sustain consumer demand and restraint of the divorce between potential output growth rate and the final demand39 have been faced by allowing households to get indebted beyond any reasonable limit. To reach this aim new financial vehicles have been created.
Both phenomena have provided the spark for the explosion of the financial crisis in 2007-2008 and the world Great Recession that yet works.
In sum, aims to eliminate (or reduce) undesired excess capacity and restore (get closer to) equilibrium firms are “doomed” to change their investment behaviour. The information relative to the level and the structure of excess capital accumulated because of past investment decisions could be a useful starting point in formulating “evolutionary hypotheses” which is functional to decisions for changing their investment routines in the light of revised expectations models. It establishes, in virtue of the time-consuming nature of these actions, an indissoluble causal link either temporal, between successive time periods, or logical, connecting indissolubly short and long period40. However, since this action takes time, their effects can be evaluated only with delay. This could determine mistaken expectations, as well as a multitude of inconsistent planes, and more unbalances. More unbalances, in turn, could generate new credit necessities and pose new constraints to short period decisions, in a continuous sequence of constraints-decisions-constraints (see Amendola and Gaffard [66]). In other terms unbalances could be, at the same time, the point of starting and/or end of economic dynamics, opening the way for further changes. Endogenous and a priori non-predictable events are likely to be encountered along this process. It prevents us to resort to optimising theory, we study the problem of efficiently utilising a given productive capacity, we study the dynamic behaviour of the economy. In other terms, when dynamic phenomena appear, “the previously existing productive structure is disturbed, its way of functioning is affected, its harmony over time, assured in the previous equilibrium state, is perturbed” (Amendola and Gaffard [79]). Rather, numerical simulations may be the best way to carry out the task41.
In conclusion, the persistence of excess capacity re-proposes the actuality of a vision of a market economy evolving only through irregular fluctuations and unbalances as well known to Schumpeter, and after him to Hicks, Samuelson, Tinbergen, Kalecky, Goodwin and others, who tried to address the topic into mathematical constructs. As it is well known, this vision is very far from mainstream modern macroeconomics, which interprets economic fluctuations as orderly dynamics42, where the plans of the economic agents are fully compatible over time and excess capacity is always null43. However, as put in Punzo ([88]), the task to undertake an alternative way was overly ambitious for those times and the mathematics at hand and the Schumpeterian vision got lost in the process of formalization. Today, by means of recent developments in computer software, the time is mature in order to undertake that road newly and attempt to unify the analysis of macro topics such as cycles, growth, technological innovation, equilibrium and disequilibrium, and the role of money. Although, I am aware that this task is formidable I think that the notion of equilibrium with undesired excess capacity proposed in this paper could be useful to build formal framework consistent with this aim.
REFERENCES
- World Bank, “Global Economic Prospects 2010: Crisis, Finance and Growth,” World Bank, Washington, DC, 2010.
- World Bank, “Global Economic Prospects 2011: Navigating Strong Currents,” World Bank, Washington, DC, 2011.
- J. Bain, “Barriers to New Competition,” Cambridge, Mass.: Harvard Univ. Press. 1956
- P. Sylos Labini, “Oligopolio e Progresso Tecnico,” Nuova Edizione, Einaudi, Torino, 1961.
- J. Steindl, “Maturity and Stagnation in American Capitalism,” Blackwell, Oxford, 1952.
- M. Spence, “Entry, Capacity, Investment and Oligopolistic Pricing,” Bell Journal of Economics, Vol. 8, No. 2, 1977, pp. 534-544. http://dx.doi.org/10.2307/3003302
- A. Dixit, “A Model of Duopoly Suggesting a Theory of Entry Barriers,” Bell Journal of Economics, Vol. 10, No. 1, 1979, pp. 20-32. http://dx.doi.org/10.2307/3003317
- G. Marini and A. Pannone, “Capital and Capacity Utilization Revisited. A Theory for ICT-Assisted Production System,” Structural Change and Economic Dynamics, Vol. 18, No. 2, 2007, pp. 231-248. http://dx.doi.org/10.1016/j.strueco.2007.01.001
- T. Kretschmer, “Information and Communication Technologies and Productivity Growth: A Survey of the Literature,” OECD Digital Economy Papers, No. 195, OECD Publishing, 2012. http://dx.doi.org/10.1787/5k9bh3jllgs7-en
- T Bresnahan and M. Trajtenberg, “The Division of Inventive Labour and the Extent of the Market,” In: E. Helpman, Ed., General Purpose Technologies and Economic Growth, MIT Press, Cambridge, 1998.
- P. Sraffa, “Sulle Relazioni tra Costo e Quantità Prodotta,” Annali di Economia, repr. In P. Sraffa, Saggi, il Mulino, Bologna, 1986. 1925
- P. Sraffa, “The Law of Returns under Competitive Conditions,” The Economic Journal, Vol. 36, No. 144, 1926, pp. 535-50.
- M. Kalecki, “Selected Essaysin the Dynamics of the Capitalist Economy,” Cambridge University Press, 1971.
- J. Halevi and P. Kriesler, “Kalecki, Classical Economics and the Surplus Approach,” Review of Political Economy, Vol. 3, No. 1, 1991, pp. 79-92. http://dx.doi.org/10.1080/09538259100000006
- E. Hein, M. Lavoie and T. van Treeck, “Some Instability Puzzles in Kaleckian Models of Growth and Distribution: A Critical Survey,” Cambridge Journal of Economics, Vol. 35, No. 3, 2011, pp. 587-612. http://dx.doi.org/10.1093/cje/beq026
- A. Turner, “The Crisis, Conventional Economic Wisdom, and Public Policy,” Industrial and Corporate Change, Vol. 19, No. 5, 2010, pp. 1317-1329. http://dx.doi.org/10.1093/icc/dtq042
- F. Donzelli, “Topics in the History of Equilibrium Analysis,” Lesson 1, Ph.D. Program in Economics University of York, 2008, p. 3.
- L. Walras, “Principe d’une Théorie Mathématique de l’Échange,” Séances et travaux de l’Académie des sciences morales et politiques (Institut de France), Collection, 33e année, nouvelle série, 101, tome I, Paris, Alphonse Picard, Janvier, 1987, pp. 97-116.
- L. Walras, “Etudes d’Économie Sociale: Théorie de la Répartition de la Richesse Sociale,” F. Rouge, Lausanne, 1896.
- V. Pareto, “Cours d’Économie Politique. Tome I,” Nouvelle édition par G.-H. Bousquet et G. Busino, Librairie Droz, Genève, 1964.
- V. Pareto, “Cours d’Économie Politique. Tome II,” Nouvelle édition par G.-H. Bousquet et G. Busino, Librairie Droz, Genève, 1964.
- K. Arrow and G. Debreu, “Existence of an Equilibrium for a Competitive Economy,” Econometrica, Vol. 22, No. 3, 1954, pp. 265-290. http://dx.doi.org/10.2307/1907353
- A. Marshall, “Principles of Economics,” Prometheus Books, Arbridged, 1890.
- K. Wicksell, “Interest and Prices,” M. Kelley, New York, 1898.
- A. Pigou, “The Economics of Stationary States,” Macmillan, London, 1935.
- K. Arrow and F. Hahn, “General Competitive Analysis,” Holden-Day, San Francisco, 1971.
- P. Tani, “Flows, Funds, and Sectoral Interdependence in the Theory of Production,” Politcal Economy-Studies in the Surplus Approach, Vol. 4, 1988, pp. 3-21.
- P. Wicksteed, “An Essay on the Co-ordination of the Laws of Distribution,” 1932 Edition, Reprint No. 12, London School of Economics, London, 1894.
- N. Georgescu-Roegen, “Man and Production,” In: M. Baranzini and R. Scazzieri, Eds., Foundations of Economics, Blackwell, Oxford, 1986.
- H. Kurt and N. Salvadori, “Theory of Production: A Long-Period Analysis,” Cambridge University Press, Cambridge, 1995. http://dx.doi.org/10.1017/CBO9780511625770
- M. Amendola and J. L. Gaffard, “The Market Way to Riches. Beyond the Myth,” Edward Elgar, 2006.
- A. Blinder, E. Canetti, D. Lebow and J. Rudd, “Asking about Prices: A New Approach to Understanding Price Stickiness,” Russell Sage foundation, New York, 1998.
- M. Bils and P. Klenow, “Some Evidence on the Importance of Sticky Prices,” Journal of Political Economy, Vol. 112, No. 5, 2004, pp. 947-985. http://dx.doi.org/10.1086/422559
- E. Dhyne, L. Álvarez, H. Le Bihan, G. Veronese, D. Dias, J. Hoffmann, N. Jonker, P. Lünnemann, F. Rumler and J. Vilmunen, “Price Setting in the Euro Area: Some Stylized Facts From Individual Consumer Price Data,” Journal of Economic Perspectives, 2006, pp. 947-985.
- A. Wolman, “Managerial and Decision Economics,” Special Issue: Price Rigidity and Flexibility: Recent Theoretical Developments, Vol. 28, No. 6, 2007, pp. 531-552.
- E. Nakamura and J. Steinsson, “Five Facts about Prices: A Reevaluation of Menu Cost Models,” The Quarterly Journal of Economics, Vol. 123, No. 4, 2008, pp. 1415- 1464. http://dx.doi.org/10.1162/qjec.2008.123.4.1415
- R. Kauffman and C. Wood, “Follow the Leader: Price Change Timing and Strategic Pricing in E-Commerce,” Managerial and Decision Economics, Vol. 28, No. 7, 2007, pp. 679-700. http://dx.doi.org/10.1002/mde.1375
- M. Bergen, S. Dutta, D. Levy, M. Ritson and M. Zbaracki, “Shattering the Myth of Costless Price Changes: A Framework for Dynamic Pricing,” European Management Journal, Vol. 21, No. 6, 2003, pp. 663-669. http://dx.doi.org/10.1016/j.emj.2003.09.018
- R. Kauffman and D. Lee, “Should We Expect Less Price Rigidity in the Digital Economy?” In: R. Sprague, Ed., Proceedings of the 37th Hawaii International Conference on System Sciences, Los Alamitos, 5-8 January 2004.
- M. Arbatskaya and M. Baye, “Are Prices ‘Sticky’ Online? Market Structure Effectsand Asymmetric Responses to Cost Shocks in Online Mortgage Markets,” International Journal of Industrial Organization, Vol. 22, No. 10, 2004, pp. 1443-1462. http://dx.doi.org/10.1016/j.ijindorg.2004.11.001
- P. Milgrom and J. Rroberts, “Complementarities and Fit: Strategy, Structure, and Organizational Change in Manufacturing”, Journal of Accounting and Economics, Vol. 19, No. 2-3, 1995, pp. 179-208. http://dx.doi.org/10.1016/0165-4101(94)00382-F
- M. Morroni, “Production Process and Technical Change,” Cambridge University Press, Cambridge, 1992. http://dx.doi.org/10.1017/CBO9780511599019
- A. Pannone, “Production, Unemployment and Wage Flexibility in an ICT-Assisted Economy. A Model,” Structural Change and Economic Dynamics, Vol. 21, No. 3, 2010, pp. 219-230. http://dx.doi.org/10.1016/j.strueco.2010.05.002
- P. Bruun and R. N. Mefford, “Lean Production and the Internet,” International Journal of Production Economics, Vol. 89, No. 3, 2004, pp. 247-260. http://dx.doi.org/10.1016/j.ijpe.2003.10.007
- H. Varian, “Computer Mediated Transactions,” Working Paper, Univ. of California at Berkley, 2010.
- N. Georgescu-Roegen, “Process in Farming versus Process in Manufacturing: A Problem of Balanced Development,” In: G. U. Papi and C. Nunn, Eds., Economic Problems of Agriculture in Industrial Societies, Macmillan, London, 1969.
- N. Georgescu-Roegen, “The Entropy Law and the Economic Process,” 4th Edition, Harvard University Press, Cambridge, 1981.
- R. Scazzieri, “A Theory of Production Tasks, Processes, and Technical Practices,” Clarendon Press, Oxford, 1993.
- P. Piacentini, “Time-Explicit Theory of Production: Analytical and Operational Suggestions Following a “FundFlow,” Approach, Structural Change and Economic Dynamics, Vol. 6, No. 4, 1995, pp. 461-483. http://dx.doi.org/10.1016/0954-349X(95)00027-K
- G. Marini and A. Pannone, “Network Production, Efficiency and Technological Options, toward a New Dynamic Theory of Telecommunications,” Economics of Innovation and New Technology, Vol. 7, No. 1, 1998, pp. 177-201. http://dx.doi.org/10.1080/10438599800000033
- A. Pannone, “Accounting and Pricing for the Telecommunications Industry. An Operational Approach,” Oxford University Press, Oxford, 2001.
- A. Graziani, “The Theory of the Monetary Circuit,” Economies et Sociétés, Monnaie et Production, Vol. 24, No. 7, 1990, pp. 7-36.
- A. Graziani, “Money as Purchasing Power and Money as a Stock of Wealth in Keynesian Thought,” In: G. Deleplace and E. Nell, Eds., Money in Motion: The Post-Keynesian and Circulation Approaches, Macmillan and St. Martin’s Press, London and New York, 1996, pp. 139- 154.
- M. Al-Shammari, “Customer Knowledge Management: People, Processess, and Technology,” 2009. http://dx.doi.org/10.4018/978-1-60566-258-9
- J. H. Gilmore and B. J. Pine, “Four Faces of Mass Customization,” Harvard Business Review, Vol. 75, No. 1, 1997, pp. 91-101.
- J. M. Keynes, “The General Theory of Employment, Interests and Money,” Macmillan, London, 1936.
- R. Hall and C. Hitch, “Price Theory and Business Behavior,” Oxford Economic Papers, Vol. 2, No. 1, 1939, pp. 12-45.
- P. Sweezy, “Demand under Conditions of Oligopoly,” Journal of Political Economy, Vol. 47, No. 4, 1939, pp. 568- 573. http://dx.doi.org/10.1086/255420
- D. Besanko, D. Dranove, M. Shanley, S. Schaefer, “Economics of Strategy,” 3rd Edition, John Wiley & Sons, Hoboken, 2004.
- L. Cabral and T. Ross, “Are Sunk Costs a Barrier to Entry?” Journal of Economics & Management Strategy, Vol. 17, No. 1, 2008, pp. 97-112. http://dx.doi.org/10.1111/j.1530-9134.2008.00172.x
- A. W. Phillips, “The Relation between Unemployment and the Rate of Change of Money Wage Rates in the United Kingdom, 1861-1957,” Economica, Vol. 25, No. 100, 1958, pp. 283-299. http://dx.doi.org/10.1111/j.1468-0335.1958.tb00003.x
- M. Ivaldi, B. Jullien, P. Rey, P. Seabright and J. Tirole, “The Economics of Tacit Collusion,” 2003.
- W. Baumol, J. Panzar and R. Willig, “Contestable Markets and the Theory of Industry Structure,” Harcourt Brace Jovanovich, Inc., New York, 1982.
- F. Hayek, “Prices and Production,” 1st Edition, Routledge and Sons, London, 1931.
- F. Hayek, “Monetary Theory and the Trade Cycle,” Reprinted in Economic Classic Series, Augustus M. Kelley, New York, 1933.
- M. Amendola and J. L. Gaffard, “The Innovative Choice,” Basil Blackwell, Oxford, 1988.
- H. Minsky, “Can ‘It’ Happen Again? Essays on Instability and Finance,” M. E. Sharpe, Armonk, 1982.
- E. Lindhal, “A Note on the Dynamic Pricing Problem,” In: J. Keynes, Ed., The General Theory and after. A Supplement. Selected Writings, Macmillan, London, 1979.
- F. Hahn, “On the Notion of Equilibrium in Economics, in Augural Lecture,” Cambridge University Press, Cambridge, 1974..
- E. Penrose, “Theory of the Growth of the Firm,” B. Blackwell, Oxford, 1959.
- D. Teece, “Toward an Economic Theory of the Multiproduct Firm,” Journal of Economic Behaviour and Organization, Vol. 3, No. 1, 1982, pp. 39-63.
- M. Weitzman, “Recombinant Growth,” Quarterly Journal of Economics, Vol. 113, No. 2, 1998, pp. 331-360. http://dx.doi.org/10.1162/003355398555595
- C. Antonelli, J. Krafft and F. Quatrar, “Recombinant Knowledge and Growth: The Case of ICTs’,” Structural Change and Economic Dynamics, Vol. 21, No. 1, 2010, pp. 50-69. http://dx.doi.org/10.1016/j.strueco.2009.12.001
- E. Brynjolfsson and A. Saunders, “Wired for Innovation: How Information Technology Is Reshaping the Economy,” The MIT Press, Cambridge, 2009.
- T. Espino-Rodriguez and V. Padron-Robaina, “A Review of Outsourcing from the Resource-Based View of the Firm,” International Journal of Management Reviews, Vol. 8, No. 1, 2006, pp. 49-70. http://dx.doi.org/10.1111/j.1468-2370.2006.00120.x
- D. Farrell, “Offshoring: Value Creation through Economic Change,” Journal of Management Studies, Vol. 42 No. 3, 2005, pp. 675-683. http://dx.doi.org/10.1111/j.1467-6486.2005.00513.x
- R. Lawrence, “Blue-Collar Blues: Is Trade to Blame for Rising US Income Inequality?” 2008.
- M. Amendola and J. L. Gaffard, “Capitalism Dynamism: Efficiency and Fairness,” 2009.
- M. Amendola and J. L. Gaffard, “Out of Equilibrium,” Economic Press Oxford, Oxford, 1998. http://dx.doi.org/10.1093/0198293801.001.0001
- F. Kydland and E. Prescott, “Time to Build and Aggregate Fluctuations,” Econometrica, Vol. 50, No. 6, 1982, pp. 1345-1370. http://dx.doi.org/10.2307/1913386
- J. Long and C. Plosser, “Real Business Cycle,” Journal of Political Economy, Vol. 91, No. 1, 1983, pp. 39-69. http://dx.doi.org/10.1086/261128
- P. Romer, “Increasing Returns and Long Run Growth,” Journal of Political Economy, Vol. 94, No. 5, 1986, pp. 1002-1037. http://dx.doi.org/10.1086/261420
- R. Lucas, “On the Mechanics of Economic Development,” Journal of Monetary Economics, Vol. 22, No. 1, 1988, pp. 2-42. http://dx.doi.org/10.1016/0304-3932(88)90168-7
- S. Rebelo, “Long-Run Policy Analysis and Long-Run Growth,” Journal of Political Economy, Vol. 99, No. 3, 1991, pp. 500-521. http://dx.doi.org/10.1086/261764
- R. Solow, “Siena Lectures on Endogenous Growth Theory,” Collana del Dipartimento di Economia Politica, Università degli Studi di Siena, 1992.
- D. Cass, “Optimum Growth in an Aggregative Model of Capital Accumulation,” The Review of Economic Studies, Vol. 32, No. 3, 1965, pp. 233-240. http://dx.doi.org/10.2307/2295827
- R. Solow, “A Contribution to the Theory of Economic Growth,” Quarterly Journal of Economics, Vol. 70, No. 1, 1956, pp. 65-94. http://dx.doi.org/10.2307/1884513
- L. Punzo, “Preface in Growth and Fluctuations: The Post- War Japanese Experience, in Cycles, Growth, and Structural Change,” 2001.
NOTES
1The extent of spare industrial spare capacity is only a partial and limited measure of slack in an economy, where in many countries the majority of employment and GDP is in the services and agricultural sectors. The notion of potential output is the whole economy analog of manufacturing capacity.
2For instance, the average rate of capacity utilization for the US. Industry in the period 2007-2009 has been has been equal to 76.27%. In January 2011 it edged down to 76.1 percent (Federal Reserve statistics 2010-2011).
3In the World Bank’s econometric model (see [1] and [2]) estimations of potential output is based on a constant returns-to-scale Cobb-Douglas production function with fixed factor share parameters and Hicks-neutral technology. Potential output is thus the level of output attained when the entirety of the capital stock and effective labor supply is employed, while total factor productivity (TFP) is growing at its trend rate. The output gap (or economy wide capacity utilization) in turn refers to the gap between actual and potential GDP.
4Clearly, undesired excess capacity has to be distinct from desired excess capacity that, in many microeconomic analyses, results from an intentional strategic behaviour of the firms. These analyses are very different in the spirit and they go, for example, from models where the capacity utilization adjusts to a “normal” level (see Bain [3], Sylos Labini [4], Steindl [5]), to game theory models where the excess capacity hypothesis is connected to the strategic option by incumbent firms to fix a limit price that prevents the entry (see among others Spence [6], Dixit [7].
5The notion new technologies that influence the economy on a broad basis was first provided by Bresnahan and Trajtenberg [10], who coined the phrase of general-purpose technologies (GPT’s). Most positive evidence of ICT as GPT’s was found for United States data, while it is more difficult to find evidence in Europe.
6Further clarification on my assumption of generalized use of ICT in an advanced economy will be provided in Section 3 of this paper.
7As it is well known we can ascribe to Sraffa ([11,12]) the definitive statement on the incompatibility of decreasing average total costs, connected to increasing returns, and perfect competition: the opportunity to exploit increasing returns by a firm implies a rise in its efficiency which may lead it to dominate the entire market, driving all others firms out of a given sector.
8An example for all: Ken Arrow, that jointly to Debreau illustrated a perfectly competitive market economy with a fully complete set of markets to be Pareto efficient, devoted much of his work to analyze the market imperfections that made his representation inapplicable in the real world (see Turner [16]).
9These assumptions are shared by the two alternative concepts of perfectly competitive equilibrium existing in literature (see Donzelli [17]): the instantaneous competitive equilibrium concept characterizing the so-called models à la Walras (see among the others, Walras [18,19]), Pareto [20,21]), Arrow-Debreu [22]); and the neoclassical stationary equilibrium concept characterizing the so-called models à la Marshall (see among the others, Marshall [23], Wicksell [24], Pigou [25].
10Indivisibility refers to indivisible goods that appear in a production process as inputs or as output.
11In the models à la Marshall, where time structure—absent in models á la Walras—has a central role, at least in the short period, firms’ expectations may be not fulfilled and their plans of sale disappointed. By the way in the long period firms can enter into or exit from the market so to bring the stocks of goods that are available to equal the market demand (see Kurtz and Salvadori [30], Donzelli [17], Amendola and Gaffard [31]).
12Blinder et al. ([32]) have conducted a large survey of firms’ pricing practices. This survey sought quantitative information about the frequency of price adjustment, and qualitative information about the costs of price adjustment.
13It is now a well-established stylized fact that most consumer prices remain unchanged for periods that can last several months (e.g. see Bils and Klenow [33], Dhyne et al. [34], Wolman [35], Nakamura and Steinsson, [36], among many others).
14For Internet-based selling context we mean a “set of technological, organizational and managerial capabilities that permit a firm’s prices to be accessible to consumers and businesses via Web sites that sell information, goods and services, and are associated with electronic commerce” (see Kauffman and Wood [37]).
15In production without ICT, like that has characterized industrial production based on the factory system with rigid automation technology (e.g. the car industry up to the ‘90s), firms could adjust actual production to orders received only by varying the time at which they employ their machinery. Frequent adjustments can lead to institutional and organizational problems. Moreover production generates large batches that need a stable intensity of demand for final products (see [1]), without which firms incur in undesired inventories accumulation. Nowadays is in general well equipped with ICT infrastructure. However, the availability of Internet access and the adoption of basic ICT applications still vary across size-classes. Sophisticated computer networks and broadband connections are more common in larger firms.
16For a presentation of the “fund-flow” model see also Tani [27]. Interesting theoretical developments can be found in Scazzieri [48] and in Piacentini [49].
17However, some production elements enter the process and are then “incorporated” in the product (e.g. the energy). Georgescu-Roegen defines them as flows. For sake of simplicity we do not consider them in our analysis.
18Let T, the working year equal to 300 working days per year. We also assume that the average duration of the working day is 8 hours. Hence T is equal to 300 × 8= 2400 hours. The total utilization times (absorption times) of capital and labor are respectively 20 and 24 hours. If we pose T = 1 we have

19Marini and Pannone in [8] have showed that q* is smaller than or equal to the minimum efficiency scale of a continuous production process without ICT as determined by means of the original fund-flow model.
20Also the mean of  should be clear: since the absorption times of capital and labour are different in the elementary process, a subunit of capital may be idle while a worker is completing its tasks (or vice versa). This kind of inefficiency can be solved by identifying the minimum number of elementary processes (minimum batch) which it permits the total elimination of idle times at this level. It is represented by the lcm between a subunit of capital and a worker.
should be clear: since the absorption times of capital and labour are different in the elementary process, a subunit of capital may be idle while a worker is completing its tasks (or vice versa). This kind of inefficiency can be solved by identifying the minimum number of elementary processes (minimum batch) which it permits the total elimination of idle times at this level. It is represented by the lcm between a subunit of capital and a worker.
21We observe that limitations to such an assumption may exist, because of the fact that labour is a quasi-fixed factor, i.e., firms have employment contracts with their workers, and cannot adjust the mount of labour used purely based on orders received. In this case firms could resort to the realities of overtime and shift work. This assumption could be introduced in the framework without loosing generality.
22We note that the inequality sign in (18b) could mean that either the existing production capacity of the firm is not sufficiently large to satisfy the demand level or the production flow cannot exactly match the demand level because of the batches indivisibility. Since ICT make the use of capital goods more refined and more adaptable, improving the matching of inputs to output, we don’t consider the last case.
23We have already developed a multi-production framework with reference to the telecommunication sector in Marini and Pannone [50], and Pannone [51].
24The adoption of this perspective leads our approach near to the spirit of the so-called monetary circuit theory (see, among the others, Graziani [52,53].
25Clearly, we are assuming that expenditures for investment at the present period translate into capital and capacity variation of firms in the period after (see above section).
26For instance a cell phone company might market their phone to teenagers by saying that it is perfect for instant messaging with their friends, while market the same phone to professionals by saying that it is great for downloading business files. Although the cell phone company is only producing one type of phone, by marketing it in different ways it is attempting to personalize the phone to different groups of people, and this is thought of as a form of customization.
27We observe that if the demand signal were provided from the expected sales, rather than customer orders, we shall refrain from referring explicitly to short-term expectations and express the problem of production in terms of values realized. The reason for this is that, like Keynes, we believe that in the short term there is an overlap between expected and achieved results, and any distinction between ex-ante and ex-post is thus extremely dubious (see Keynes [56], pp. 208-209). In other words, even if production anticipates demand, it is as if demand generates signals that cause a continual change in the short-term expectations and thus in production, which comes to be seen as determined by the demand itself, just as in the Keynesian framework.
28At aggregate level we assume that there is always an activation scale of the elementary processes that satisfies simultaneously the sign of parity in (18a), (18b) and (25). In this way we may exclude the possibility of technological unemployment (unemployment caused by a level of capital insufficient to absorb the overall labour supply present in the system). Also we overlook the existence of frictional unemployment (unemployment that depends on the strength of intersectoral shocks and on the mobility of labour and capital).
29Since the economy produces only one commodity, to avoid circular logic we assume that the price of a capital unit at the present period (that is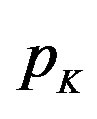 in Equation (15) and (15bis)) is equal to the commodity price in the preceding period. This assumption is consistent with the idea that capital goods are produced (and purchased) in the preceding period and take time to be operative in production (see Section 4 and note 25).
in Equation (15) and (15bis)) is equal to the commodity price in the preceding period. This assumption is consistent with the idea that capital goods are produced (and purchased) in the preceding period and take time to be operative in production (see Section 4 and note 25).
30This assumption could be derived by the original Phillips relationships [61]. It should be:
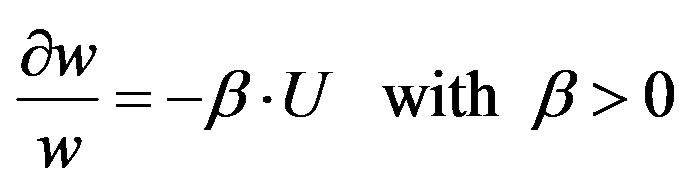 where
where
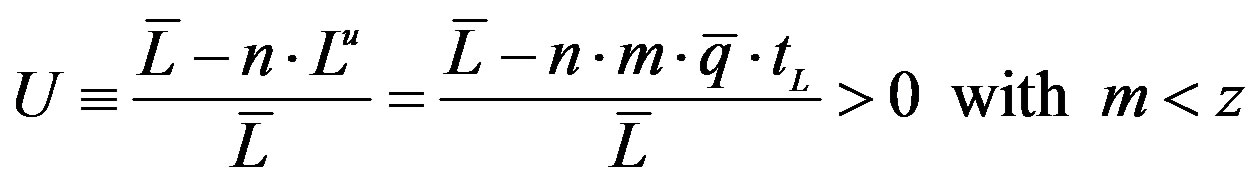
is the unemployment rate (see Equation (25)).
31As it is well known, the contractionary effect of wage reductions is a standard result in Kaleckian models of imperfect competition.
32In (28), for sake of simplicity, the normal level of utilization of capacity coincides with the full utilization.
33Equation (29) is more precise than (30) in presence of a change of the utilization level of capital (see Sylos Labini [4]).
34Clearly 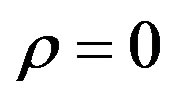 in oligopolistic setting implies that: a) leader firms charge price equal to average costs to compensate the initial fall of demand; b) incumbent firms keep down the price to counter the threat of entry of new comers (see Baumol et al. [63], Cabral and Ross [60]).
in oligopolistic setting implies that: a) leader firms charge price equal to average costs to compensate the initial fall of demand; b) incumbent firms keep down the price to counter the threat of entry of new comers (see Baumol et al. [63], Cabral and Ross [60]).
36Clearly, (34) represents ex-post sunk cost also in an oligopolistic setting if 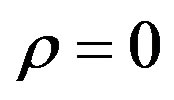 in (31). On the contrary, if
in (31). On the contrary, if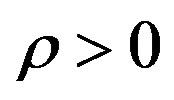 , the total cost of the unused capital may be covered by “over normal” profit. In this case this cost would not be sunk, but its presence would imply in any case reduction of actual profits.
, the total cost of the unused capital may be covered by “over normal” profit. In this case this cost would not be sunk, but its presence would imply in any case reduction of actual profits.
36Clearly, in our approach the role of credit in presence of sunk cost is crucial whatever is the market setting (perfect competition and monopoly/oligopoly). In a different way, in neoclassical equilibrium models ex-post sunk costs are always null and money is “neutral” (see Hayek [64,65]).
37In the period 2000-2006 the wage growth of workers at all but the very highest levels of skill and education has been equally poor. Slow real wage growth reflects strong profit growth (see Lawrence [77]).
38In fact whereas earlier trade pressures affected only unskilled workers, trade now puts downward pressures on the earnings of workers of all kinds because of the increased ability to offshore services electronically. A second reason is connected to the increased ability to offshore manufacturing. There is certainly evidence that US multinational firms have been expanding their employment shares in their foreign affiliates (see Lawrence [77]).
39As an example of this divorce one can see that the growth of the productivity in US in the period 1997-2006, is associated to an average rate of industrial capacity utilization in the same period (79.57%) lower than the periods 1980-1986 (79.67%) and 1987-1996 (82.47%). We have calculated the average capacity utilization rates for the US. Industry on the basis of the Federal Reserve statistics.
40Clearly we are in debt with Hicks [80] for the distinction between historical and logical causality in economics.
41Amendola and Gaffard have recently adopted a “neo-Austrian” model to simulate “out of equilibrium” dynamics associated to the process of technological innovation (see [31,66,79]).
42This is true in the Real Business Cycle (RBC) analysis (see Kydland and Prescott [80], Long and Plosser [81]), where a perfectly competitive equilibrium is always guaranteed by rational expectations and the cycles are explained as the result of the reaction of intertemporally optimizing economic agents to random (and exogenous) technological shocks. But the same is true in the “endogenous growth models” (see Romer [82], Lucas [83], Rebelo [84]), where accumulation of knowledge and R&D or education spending increase the growth rate of economy by increasing the incentive to innovate. Also in this case economic agents (consumers and firms) who have rational expectations solve an intertemporal optimization problem of an objective function (a utility or a profit function) determining the saving rate and hence the intensity of the accumulation of whatever factor is reckoned to bring about increasing returns. As in the RBC analysis the economy is always in equilibrium, condition that becomes the very way of being of economic dynamics.
43Before of RBC and the economic growth models, Solow-type models viewed growth as a steady state and focused on convergence issues. “Steady state is approached asymptotically by any optimal path from any initial conditions: starting from arbitrary initial condition the solution of the optimization problem converges to the saddle point” (Solow [85], p. 15). But while in the “optimizing” version of the approach (see Cass [86]) the economy is always in equilibrium, not only at the saddle point but also along the path followed to reach it (see Amendola and Gaffard [79], p. 110), in the Solow’s original version of the model (Solow [87]) the saddle point is a long period position that the economy may or may not be in: in fact fluctuations—in terms of inconsistency of investments and final consumption—could arise in the short run if wage and price were sticky. However, although the distinction between being in equilibrium or being out of equilibrium exists in the model, the motion toward the long period position involves a problem of “transitional dynamic” and co-ordination that is solved a priori in a steady state equilibrium and hence it cannot be analyzed by means of this framework.

