Wireless Engineering and Technology
Vol. 4 No. 4 (2013) , Article ID: 38683 , 16 pages DOI:10.4236/wet.2013.44029
Parallel Algorithms for Residue Scaling and Error Correction in Residue Arithmetic
![]()
Department of Electrical Engineering, National Tsing Hua University, Hsinchu City, Chinese Taipei.
Email: hylo@ee.nthu.edu.tw
Copyright © 2013 Hao-Yung Lo, Ting-Wei Lin. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 3rd, 2013; revised September 11th, 2013; accepted September 30th, 2013
Keywords: Chinese Remainder Theorem (CRT); Error Correction; Error Detection; Parallel Residue Scaling; Residue Number Systems (RNS); Target Race Distance (TRD); Target Residue-Digit Difference
ABSTRACT
In this paper, we present two new algorithms in residue number systems for scaling and error correction. The first algorithm is the Cyclic Property of Residue-Digit Difference (CPRDD). It is used to speed up the residue multiple error correction due to its parallel processes. The second is called the Target Race Distance (TRD). It is used to speed up residue scaling. Both of these two algorithms are used without the need for Mixed Radix Conversion (MRC) or Chinese Residue Theorem (CRT) techniques, which are time consuming and require hardware complexity. Furthermore, the residue scaling can be performed in parallel for any combination of moduli set members without using lookup tables.
1. Introduction
Because the residue number system (RNS) operations on each residue digit are independent and carry free property of addition between digits, they can be used in highspeed computations such as addition, subtraction and multiplication. To increase the reliability of these operations, a number of redundant moduli were added to the original RNS moduli [RRNS]. This will also allow the RNS system the capability of error detection and correction. The earliest works on error detection and correction were reported by several authors [1-12]. Waston and Hasting [1,2] proposed the single residue digit error correction. Yau and Liu [3] suggested a modification with the table lookups using the method above. Mandelbaum [4-6] proposed correction of the AN code. Ramachandran [7] proposed single residue error correction. Lenkins and Altman [8-10] applied the concept of modulus projection to design an error checker. Etzel and Jenkins [11] used RRNS for error detection and correction in digital filters. In [12-16] an algorithm for scaling and a residue digital error correction based on mixed radix conversion (MRC) was proposed. Recently Katti [17] has presented a residue arithmetic error correction scheme using a moduli set with common factors, i.e. the moduli in a RNS need not have a pairwise relative prime.
In this study, we developed two new algorithms without using MRD (Mixed-radix digit) or CRT (Chinese remained Theorem) for speeding-up the scaling processes and simplifying the error detection and correction in RNS. The first algorithm is used for these purposes, through the residue digit difference cyclic property (CPRDD) within the range of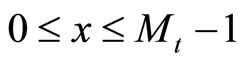 , where
, where 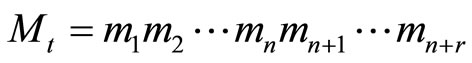 with r additional moduli. The moduli
with r additional moduli. The moduli  are called the nonredundant moduli;
are called the nonredundant moduli; 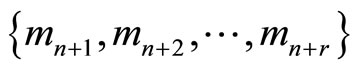 are the redundant moduli. The interval,
are the redundant moduli. The interval, 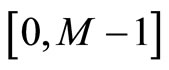 , is called the legitimate range, where
, is called the legitimate range, where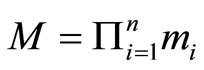 , and the interval,
, and the interval,
 , is the illegitimate range, where
, is the illegitimate range, where
 , and
, and 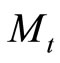 is the total range. This paper is organized as follows: Section II will describe the scheme the cyclic property of residue digit difference (CPRDD). Section III describes the Target Race Distance (TRD) algorithm and followed by some examples. Section IV discusses residue scaling and error correction using the TRD and CPRDD algorithms. Finally, the conclusion is given in section V.
is the total range. This paper is organized as follows: Section II will describe the scheme the cyclic property of residue digit difference (CPRDD). Section III describes the Target Race Distance (TRD) algorithm and followed by some examples. Section IV discusses residue scaling and error correction using the TRD and CPRDD algorithms. Finally, the conclusion is given in section V.
2. Error Detection and Correction Using Residue Digit Difference Cyclic Property
Any residue digit xi representation in moduli set
 has its cyclic length with respect to its module number. For example, if the moduli set is (4, 5, 7, 9), then the cyclic lengths of any residue digits
has its cyclic length with respect to its module number. For example, if the moduli set is (4, 5, 7, 9), then the cyclic lengths of any residue digits
 are 4, 5, 7 and 9, respectively. Since these cyclic lengths are not equal, they are very difficult to use as tools for error detection and correction. Actually, there exists the property of common (uniform) cyclic length in RNS between residue digital-differences (RDD). Consider three moduli set
are 4, 5, 7 and 9, respectively. Since these cyclic lengths are not equal, they are very difficult to use as tools for error detection and correction. Actually, there exists the property of common (uniform) cyclic length in RNS between residue digital-differences (RDD). Consider three moduli set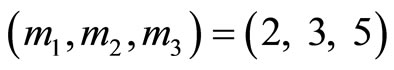 . The residue representations and their corresponding digit-differences are shown in Table 1 and defined as the difference in value between two digits,
. The residue representations and their corresponding digit-differences are shown in Table 1 and defined as the difference in value between two digits, 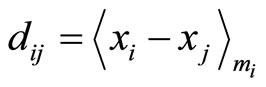 where
where 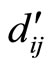 s are all modulo to positive values with respect to
s are all modulo to positive values with respect to  if the cycle length of
if the cycle length of 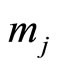 is assigned.
is assigned.
Note that the residue digit-differences 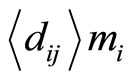 in Table 1 are obtained from
in Table 1 are obtained from 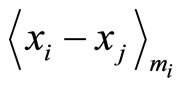 if
if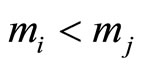 , and from
, and from 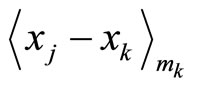 if
if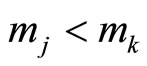 . This difference of
. This difference of
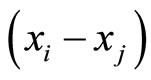 or
or 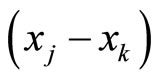 in values may be positive or negative, depending upon
in values may be positive or negative, depending upon  or
or 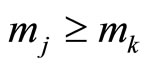 and
and
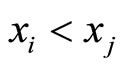 or
or 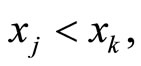 respectively All negative values must be modulo to positive values. For example, on starred row 28, as shown in Table 1, the digit difference in value for
respectively All negative values must be modulo to positive values. For example, on starred row 28, as shown in Table 1, the digit difference in value for 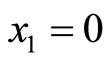 and
and 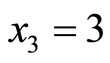 is
is
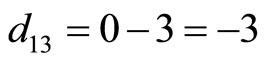 . It results in
. It results in 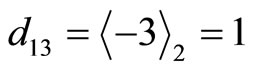
From the cyclic property of residue-digit difference (CPRDD) in RNS, we now have the following theorem.
Theorem 1. For a moduli set
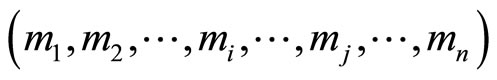 and residue representation for
and residue representation for 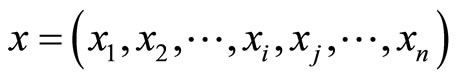 in RNS, there exists a cyclic property in differences between two residue digits,
in RNS, there exists a cyclic property in differences between two residue digits,
 or
or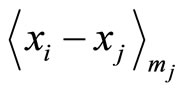 . The cyclic length can be assigned, either to
. The cyclic length can be assigned, either to  or
or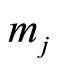 , depending upon modulo operation with respect to
, depending upon modulo operation with respect to 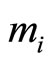 or
or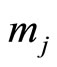 .
.
Proof: Consider the case respective to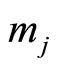 , the residue-digit difference (RDD) between two digits in
, the residue-digit difference (RDD) between two digits in
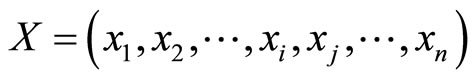 can be in general expressed by the equation
can be in general expressed by the equation
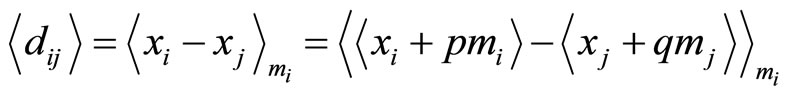 (2-1)
(2-1)
where 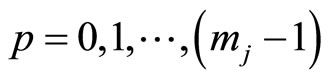

and 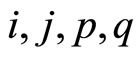 are integers.
are integers.
For simplicity, we only consider the case of  and assume
and assume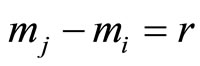 , and the case of
, and the case of  can be obtained in a similar way.
can be obtained in a similar way.
The related theorem and algorithm are described as follows.
1) In cycle 0, (the initial cycle), we have
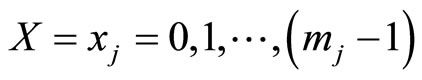 with
with ,
,
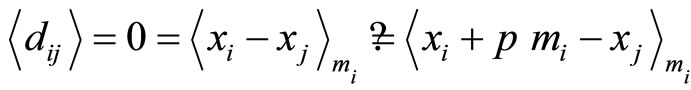 As
As 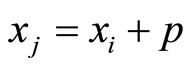

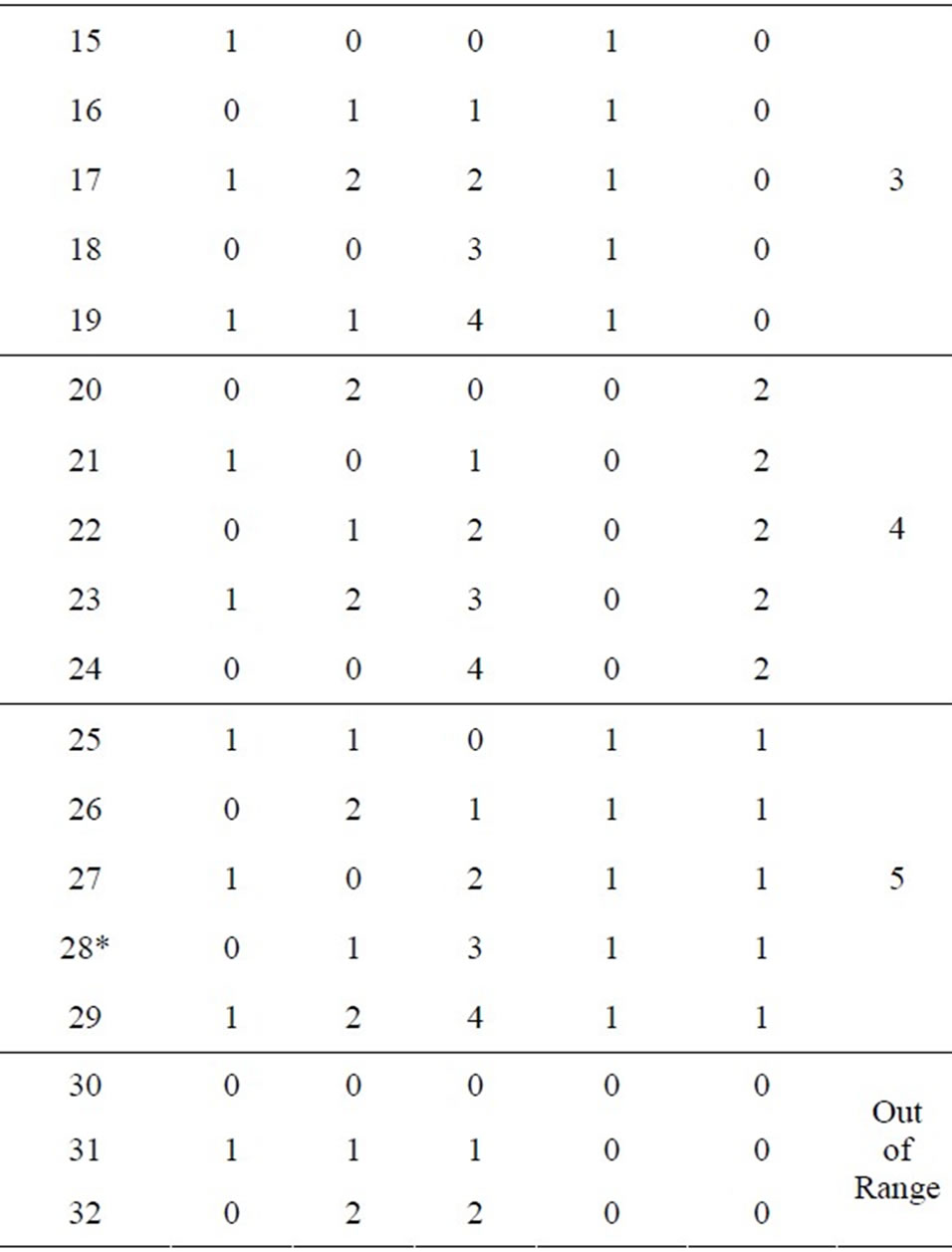
Table 1. Cyclic property of Residue Digit Difference.
 with
with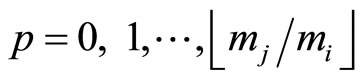 , we have
, we have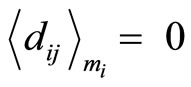 with mj’s 0s in cycle 0, where
with mj’s 0s in cycle 0, where 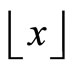 means the largest integer less than or equal to x.
means the largest integer less than or equal to x.
Thus, the RDD has mj’s “0” in the initial cycle for each modulus, i.e., in cycle 0, 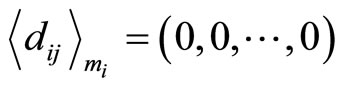 for all
for all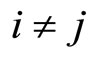 .
.
2) Next consider each modulus Since
Since  and
and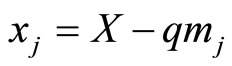 then
then
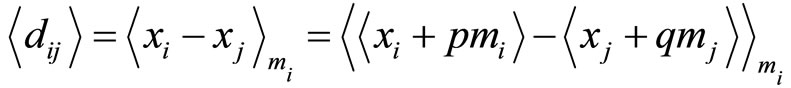 where
where
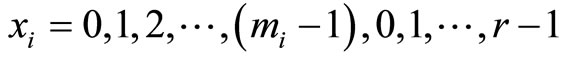

For RDD = 0 (for cycles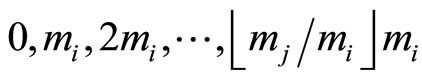 )
)
then

with mj’s 0 s.
For RDD = 1 (not necessary in cycle 1),
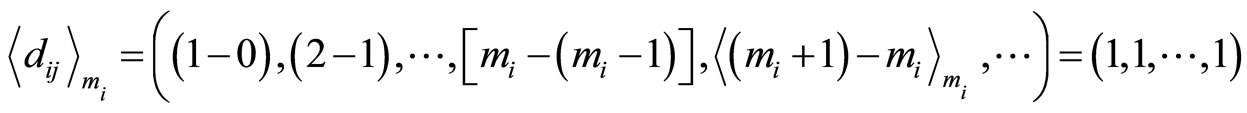 with mj’s 1 s.
with mj’s 1 s.
…
For RDD = mi − 1
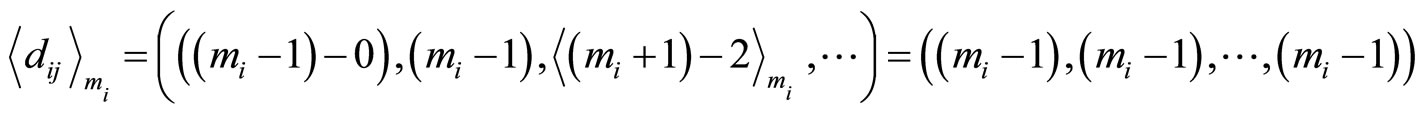
with 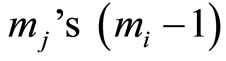 s.
s.
Corollary 1. From the above theorem, we can immediately obtain that each cycle in the residue-digit difference of x will start at location 0, and end at location
 .
.
Corollary 2. It is easily shown that there exists mi number of cycles with respect to the cyclic length of .
.
Proof. Since the residue-digit difference of
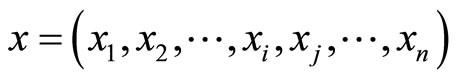 representation is pair-wise, the legitimate range of this pair-wise
representation is pair-wise, the legitimate range of this pair-wise 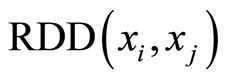 is
is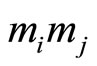 , (from 0 through
, (from 0 through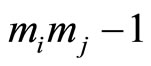 ). From corollary 1, the cyclic length is
). From corollary 1, the cyclic length is . Thus the number of cycles within this cyclic length for
. Thus the number of cycles within this cyclic length for 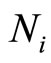 is
is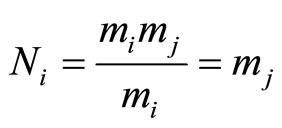 , and for
, and for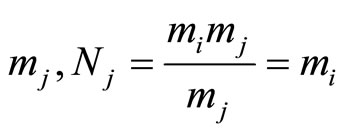 .
.
Theorem 2. The algorithm of theorem 1 and its corollaries can be extended to two or more pair-wise residuedigit differences.
Proof: consider a three moduli set, we have two pairwise moduli sets, whose RDD (Residue Digital Difference) is

where 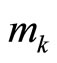 is again the referenced module.
is again the referenced module.
Follow the same procedure as step (2) as above.
Assume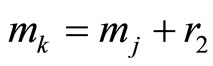 , and also pair-wise numbers
, and also pair-wise numbers
 and
and
 .
.
1) For 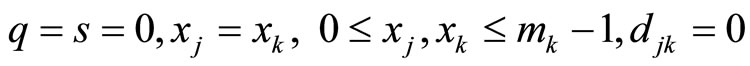
thus
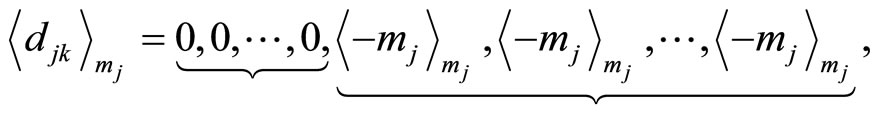
 “0” r2’s “
“0” r2’s “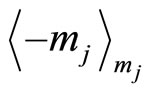 ”
”
This shows that 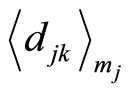 has also
has also  “0”s in cycle 0 of
“0”s in cycle 0 of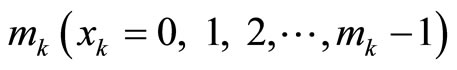 . The cyclic length is
. The cyclic length is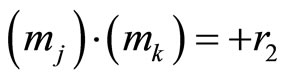 , and the number of cycles for
, and the number of cycles for 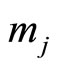 is
is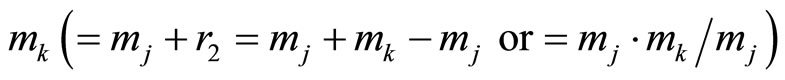 .
.
2) For 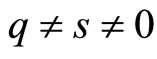 and
and 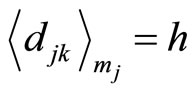 (a constant for any RDD), if
(a constant for any RDD), if 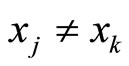
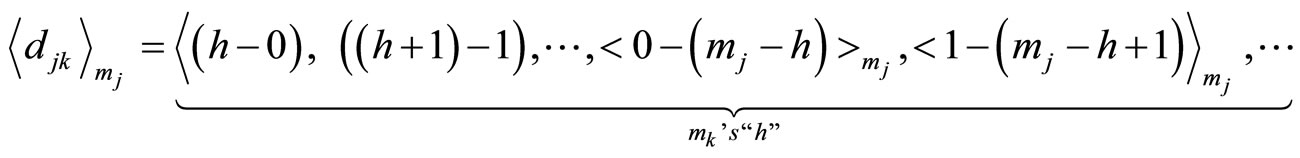
This shows that the 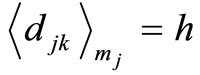 in any location has also
in any location has also 
 in cycle i of
in cycle i of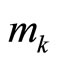 . The number of cycles for
. The number of cycles for 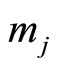 is still
is still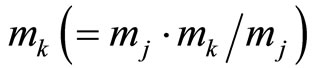 . Combining these three moduli
. Combining these three moduli  into one set, we have cyclic length
into one set, we have cyclic length 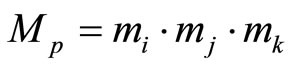 (for example,
(for example,
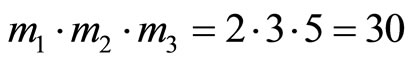 ). The number of cycles for
). The number of cycles for
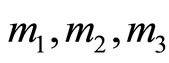 are
are ,
,
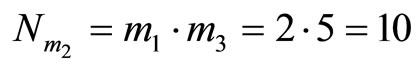 , and
, and , respectively. As shown in Table 1, the RDD pairs of
, respectively. As shown in Table 1, the RDD pairs of
 , and
, and
(1, 1)
In general, 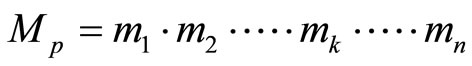 and
and
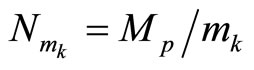 with
with 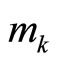 rows and
rows and 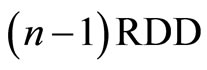 in each row.
in each row.
This completes the proof.
Example 2-1.
Consider a moduli set ,
,  and its corresponding residue digits representation set is
and its corresponding residue digits representation set is . The cyclic length is
. The cyclic length is 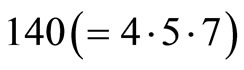 and the number of cycles for
and the number of cycles for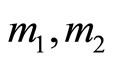 , and
, and  are
are
 , and
, and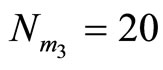 , respectively.
, respectively.
Error detection and correction:
Before the CPRDD algorithm used for error detection and correction is described, some basic terms in use must be defined.
Definition 1: Stride distance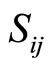 : It is the incremental or decremental distance between moduli
: It is the incremental or decremental distance between moduli 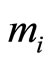 and
and  in absolute value from ith cycle to
in absolute value from ith cycle to  cycle.
cycle.
For example: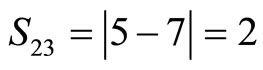 .
.
(1) Error detection Let the moduli set be
 where
where 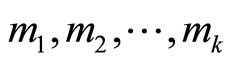 are the nonredundant moduli and
are the nonredundant moduli and  are the redundant moduli. Since the cyclic lengths of CPRDD
are the redundant moduli. Since the cyclic lengths of CPRDD 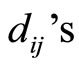 are constant, it is thus easily found that the number of cycles on track
are constant, it is thus easily found that the number of cycles on track  from the starting point 0 (or other
from the starting point 0 (or other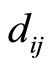 ) to its target position. In turn the distance of RDD’s can also be found.
) to its target position. In turn the distance of RDD’s can also be found.
Theorem 3. The number of cycles on track 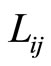 (column
(column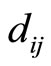 ) from any starting point (say
) from any starting point (say ) to its target position
) to its target position 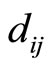 can be found using the equation below;
can be found using the equation below;
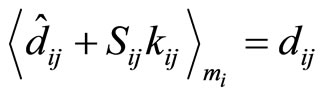
where 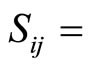 the stride distance between moduli
the stride distance between moduli 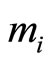 and
and  and k = the number of cycles passing through from starting point
and k = the number of cycles passing through from starting point 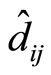 to the destination,
to the destination, 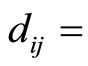 on track
on track 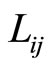 If
If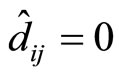 , then the number of cycles are equal to the total cycles from the starting point “0” to its target position
, then the number of cycles are equal to the total cycles from the starting point “0” to its target position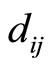 .
.
Proof: Since 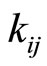 is the number of cycles from 0 to
is the number of cycles from 0 to 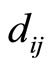 with respect to module
with respect to module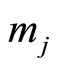 , and
, and 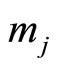 is the cyclic length, thus
is the cyclic length, thus 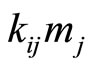 is the total distance from the starting point
is the total distance from the starting point  to its target position
to its target position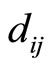 . The remaining distance for
. The remaining distance for 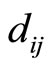 on track
on track  in the
in the 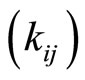 th cycle must be on the same row of
th cycle must be on the same row of 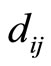 on track
on track . Thus,
. Thus,
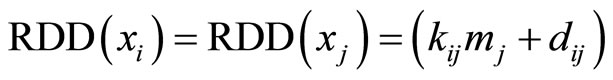 .
.
Once the RDD’s of  are found, the error detection and correction for moduli can be found just by comparing the calculated cycles or RDD with the original residue representation, pair-wise so that the error module can be detected.
are found, the error detection and correction for moduli can be found just by comparing the calculated cycles or RDD with the original residue representation, pair-wise so that the error module can be detected.
The procedure for error detection by using CPRDD algorithm is summarized as follows.
1) Choose two most significant (largest) moduli as the referred moduli among the n moduli, say  and
and .
.
2) Find the skip distance of a cycle
 .
.
3) Find the digit difference
 .
.
4) Create the equation of
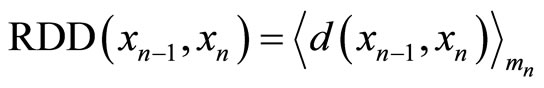 or
or
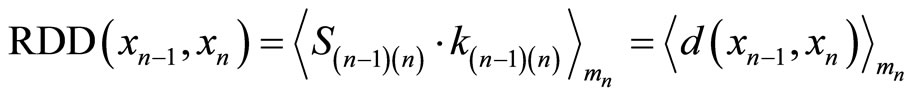 (2-2)
(2-2)
5) Solve for  from Equation (2-2) as the
from Equation (2-2) as the
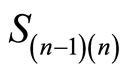 and
and  are known. The value of
are known. The value of 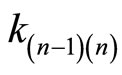 must be less than or equal to
must be less than or equal to
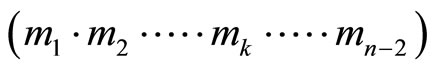 .
.
6) Find the corresponding  distance from the starting point to
distance from the starting point to .
.
7) Calculate 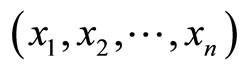 from RDD1, RDD2,
from RDD1, RDD2,  , and check the values of
, and check the values of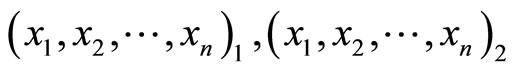 , and …. If these sets’ numbers are equal, then no error occurs; otherwise, error exists.
, and …. If these sets’ numbers are equal, then no error occurs; otherwise, error exists.
We take the similar numerical as example 2-1 to verify this algorithm. (CPRDD)
Example 2-2. Assume that a moduli set
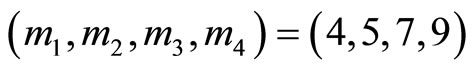 and number X whose residue representation is
and number X whose residue representation is . If an error occurs at
. If an error occurs at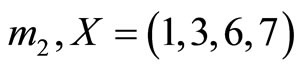 , the error detection can be described as follows.
, the error detection can be described as follows.
Let us begin our procedures from the
 . Since
. Since
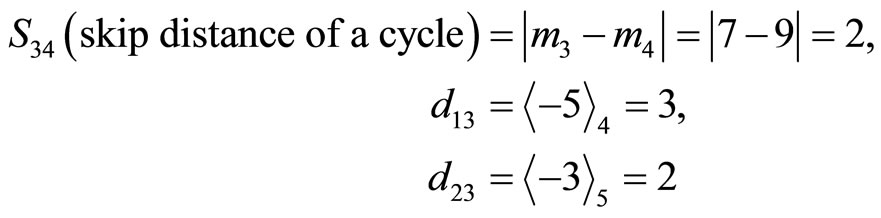 and
and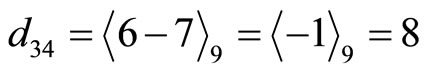 . Then
. Then
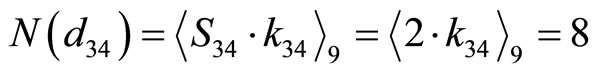 . Solve for
. Solve for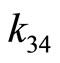 , and let
, and let 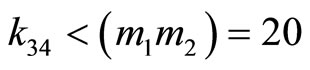 within legitimate range
within legitimate range
 , then
, then .
.
The corresponding 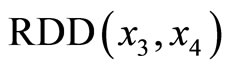 primary distances for these two
primary distances for these two 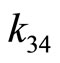 are, respectively,
are, respectively,
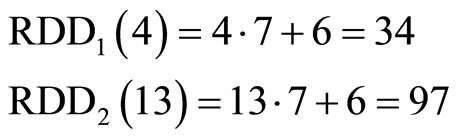
Thus, the generated results of the residue representation from 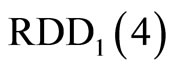 and
and 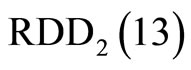 are respectively
are respectively
 ,
,
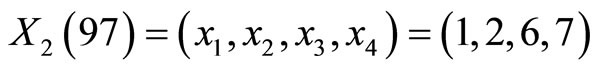 .
.
Since the calculated results of X1 and X2 are not identical, there must be errors in one of these moduli. We cannot determine which one is erroneous. To locate the module where the error exists, at least one additional (redundant) module must be used.
The procedure for error correction by using CPRDD algorithm is essential the same as the error detection. However, two additional redundant moduli 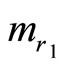 and
and 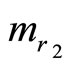 must be added for one error correction. Note that only one redundant modulus added for error detection.
must be added for one error correction. Note that only one redundant modulus added for error detection.
1) Choose 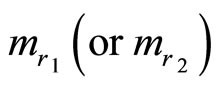 as a referred modulus.
as a referred modulus.
2) Find  as the same procedures of error detection steps 2-7.
as the same procedures of error detection steps 2-7.
3) Examine the values of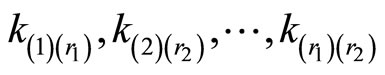 . If common value exists among,
. If common value exists among,  then no error occurs. If there is one and only one, say
then no error occurs. If there is one and only one, say 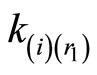 that has no common value with all other
that has no common value with all other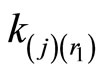 , then an error exits in modulus
, then an error exits in modulus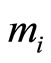 . This completes the error correction procedures.
. This completes the error correction procedures.
The following example is illustrated here to verify this algorithm.
Example 2-3. Error correction As before we can further locate and correct a single error by adding two redundant moduli,  and
and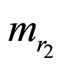 . Let us use the same example. The moduli set
. Let us use the same example. The moduli set
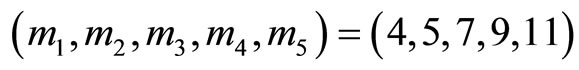 , where
, where 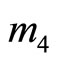 and
and 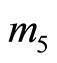 are redundant moduli
are redundant moduli 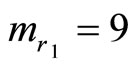 and
and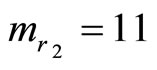 , and the residue X representation,
, and the residue X representation,
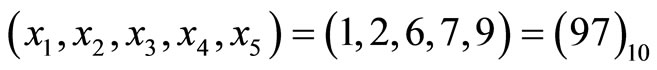 . If a single error occurs at
. If a single error occurs at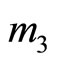 , e.g.
, e.g.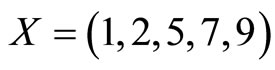 , and
, and 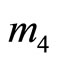 is assigned as a reference module, then
is assigned as a reference module, then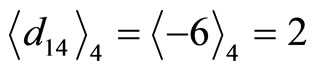 ,
, 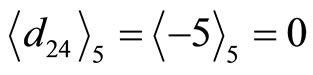 ,
, 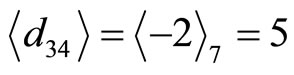 ,and
,and
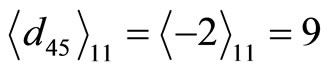 . From CPRDD algorithm, we can find the number of cycles for these RDD’s.
. From CPRDD algorithm, we can find the number of cycles for these RDD’s.
 ,
,
 ,
,
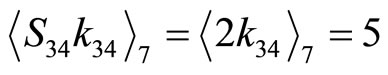 ,
,
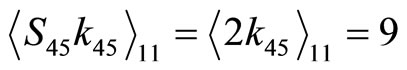
Since the cycle length is 9, all above  values must be less than
values must be less than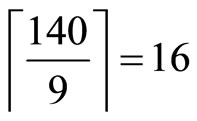 . Thus we have
. Thus we have
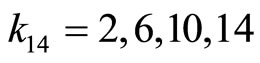

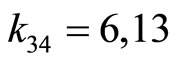 .
.

If no errors occur, all kij’s are equal, i.e.,
 .
.
Compared to the above results with pairwise moduli, only 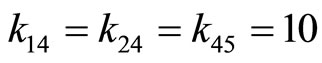 meets this condition. There exists no such value in
meets this condition. There exists no such value in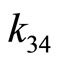 .
.
This shows that the module 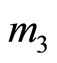 is faulty, therefore we can correct it as follows: since
is faulty, therefore we can correct it as follows: since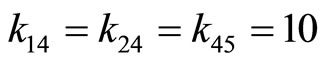 , the
, the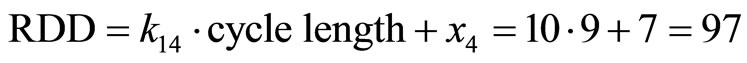 .
.
Thus 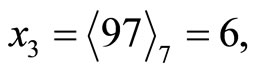

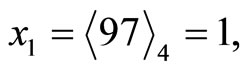
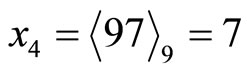 .
.
This completes the error correction.
Note that the above CPRDD’s for each residue-digit difference, 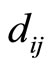 , and
, and  can be processed in parallel. In addition, if the referenced module is assigned to the erroneous module by chance, e.g.,
can be processed in parallel. In addition, if the referenced module is assigned to the erroneous module by chance, e.g., 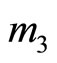 this algorithm will fail to locate the error. In this case, there are no
this algorithm will fail to locate the error. In this case, there are no 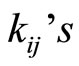 values that can be found to match this condition. The way to solve the problem is, of course, to assign any other moduli, e.g.,
values that can be found to match this condition. The way to solve the problem is, of course, to assign any other moduli, e.g., 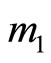 or
or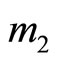 .
.
The hardware design for the proposed algorithm in Example 2-3 is shown in Figure 1.
3. The Target Race Distance (TRD) Scheme
The conversion or decoding technique from residue representation to X in binary is usually accomplished using the mixed-radix digit (MRD) or Chinese remained theorem (CRT). An optimal matched and parallel converter of this kind can be seen in [13]. The MRD is shown by the following expression with weighted numbers:
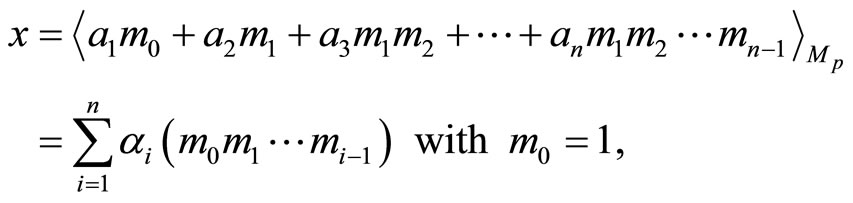
where , and
, and 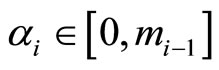 is the mixed-radix conversion (MRC) of x.
is the mixed-radix conversion (MRC) of x.
Optimization can be obtained using this method, as the accessed table lookup time is exactly equal to the right addition time, after immediate column stage for the tree network of the adders.

Figure 1. The hardware implementation for the proposed error and correction location algorithm can be accomplished without using lookup tables.
However, time is still consumed reading a large number of lookup tables. Additional hardware complexity is required by the adder-tree networks. An algorithm called the target race distance was with a simpler structure was developed for high-speed conversion.
TRD algorithm Suppose each residue number in the 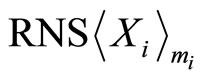 has its own track
has its own track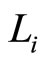 , and the distance over track
, and the distance over track 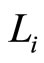 from 0 (starting point) to
from 0 (starting point) to 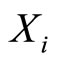 (end point) through
(end point) through  cycles can be expressed using
cycles can be expressed using
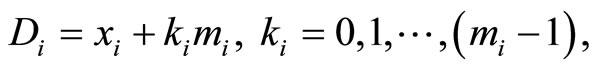 .
.
Obviously, the primary (no multiples of mi) distance of 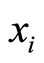 is
is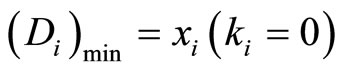 . To obtain the X from its residue representation of
. To obtain the X from its residue representation of , we must find a target such that
, we must find a target such that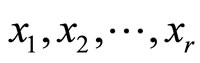 traversing the same distances over tracks
traversing the same distances over tracks 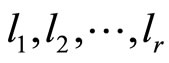 respectively, i.e. when the TRD distance of each target
respectively, i.e. when the TRD distance of each target 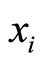 is reached, then
is reached, then 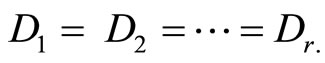 The TRD distance of X can be found from the following theorem:
The TRD distance of X can be found from the following theorem:
Theorem 4. Consider the simple case of two moduli sets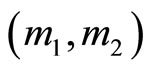 . Its residue representation and targets are x1 and x2 respectively. Let
. Its residue representation and targets are x1 and x2 respectively. Let 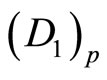 be the primary distance of residue x1 from 0 to x1 on the track
be the primary distance of residue x1 from 0 to x1 on the track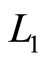 , and
, and  be the primary distance of x2 from 0 to x2 on track
be the primary distance of x2 from 0 to x2 on track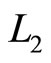 . Then the TRD distance for these two residues x1 and x2 that have the same TRD distances can be obtained by the following equation.
. Then the TRD distance for these two residues x1 and x2 that have the same TRD distances can be obtained by the following equation.
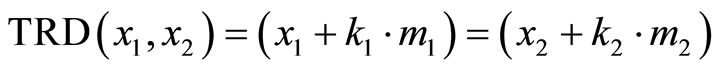 (3-1)
(3-1)
In addition, k1 can be calculated from the equation

where m1 is the cyclic length of x1, and k1 is number of cycles, all of the integers,
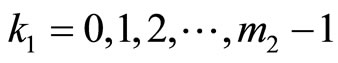 .
.
Proof: It is easy to show that the above 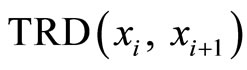 is the common target distance of x1 and x2, Since
is the common target distance of x1 and x2, Since
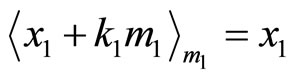
And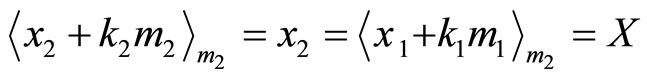 thus
thus 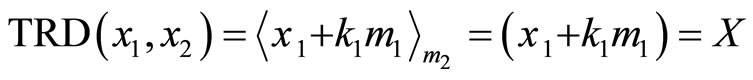 is the TRD distances for both of x1 and x2.
is the TRD distances for both of x1 and x2.
Corollary: It is evident that the above theorem can be extended to n moduli set 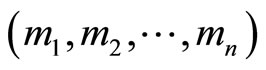 and residue number
and residue number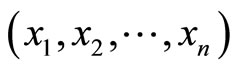 . The corresponding TRD of
. The corresponding TRD of 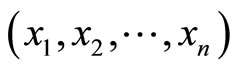 are therefore
are therefore
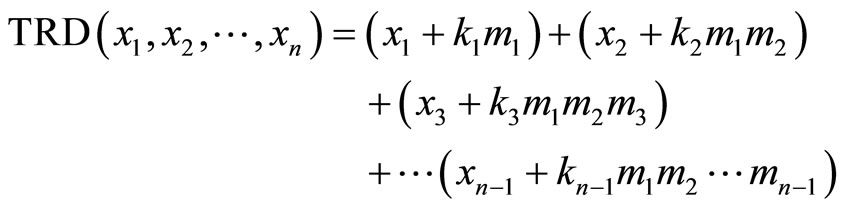
In addition, ki can be solved from the following equations.
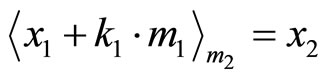
…
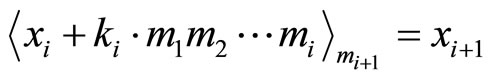
where 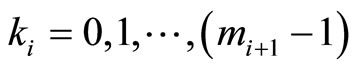
Note that  are the targets of moduli
are the targets of moduli
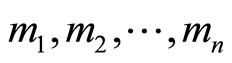 respectively and the
respectively and the 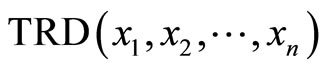 is the distance that has equal track lengths, i.e.
is the distance that has equal track lengths, i.e.
 . That is;
. That is;
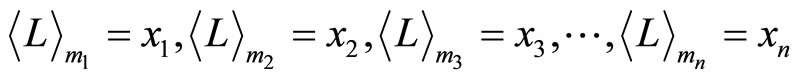 .
.
Example 3-1 Let the moduli set be
 and the residue representation be
and the residue representation be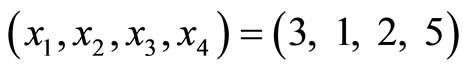 . The procedures to find the TRD distance can be described as follows:
. The procedures to find the TRD distance can be described as follows:
1) Find the primary distance 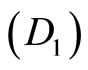 of residue
of residue
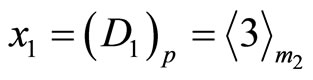 since
since 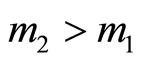 and
and 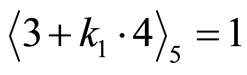
is required , thus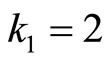 , and
, and
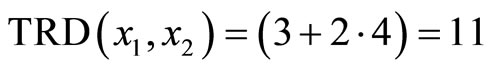
2) Repeat the procedure 1 to find the number of cycles k2 and k3 and the last TRD distances (destinations),
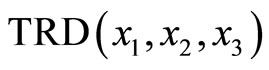 and
and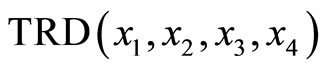 .
.
Since 
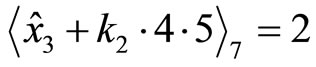
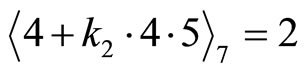
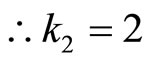
thus 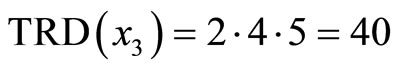
and 

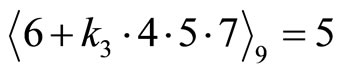

thus 
and 
The final TRD distance is the common distinction of this system for targets 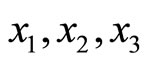 and
and  i.e.
i.e.
 . This result can be verified as follows:
. This result can be verified as follows:
 ,
,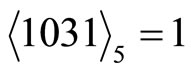 ,
,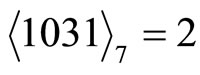 and
and 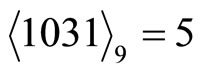
Figure 2 Shows the TRD’s on tracks 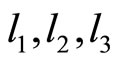 and
and 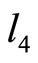 respectively.
respectively.
Error detection and correction by TRD algorithm A redundant residue number system with 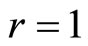 redundant moduli will allow detection of any single error [4,14]. Consider the moduli set
redundant moduli will allow detection of any single error [4,14]. Consider the moduli set
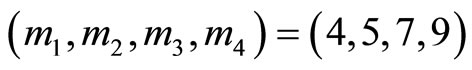 and the correct residue representation
and the correct residue representation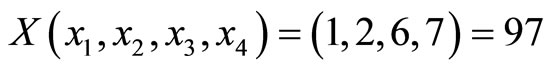 . Let us
. Let us
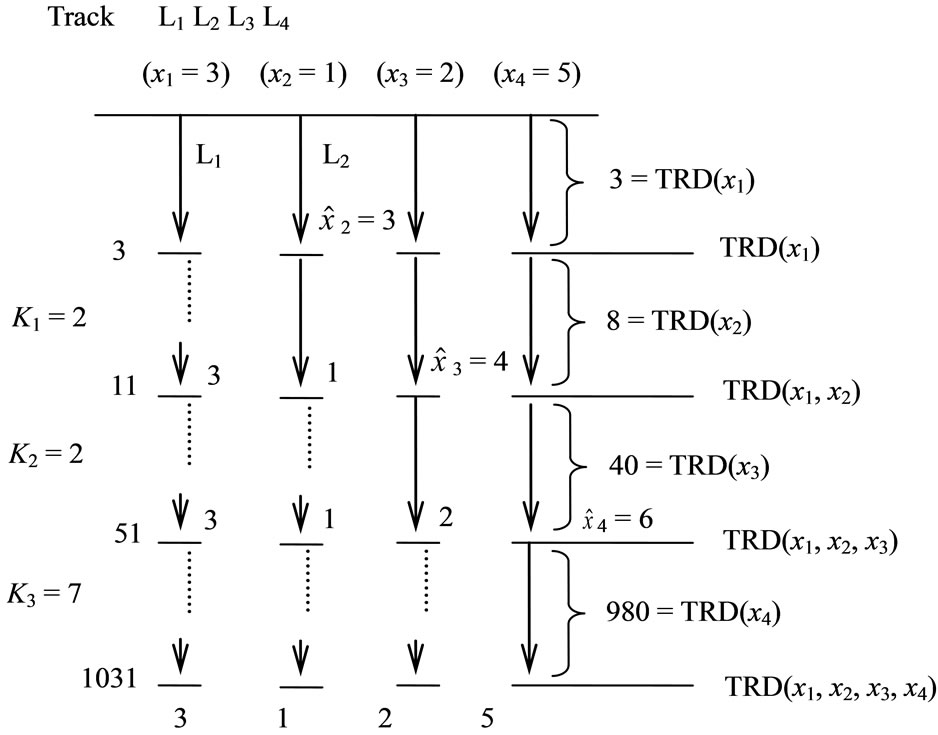
Figure 2. TRD’s on track L1, L2, L3 and L4.
assume that 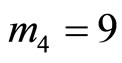 is the redundant moduli with a single error
is the redundant moduli with a single error 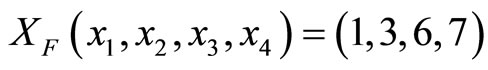 residue representation. The TRD theorem can be used to detect this error. We find that final TRD for
residue representation. The TRD theorem can be used to detect this error. We find that final TRD for 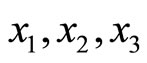 and
and 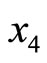 does not fall into the legitimate range as follows i.e.
does not fall into the legitimate range as follows i.e.
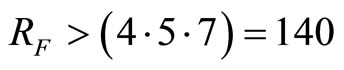

The final TRD distance
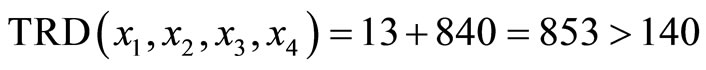 . If we need to locate and correct this module error, another redundant module must be added. Let us assume that
. If we need to locate and correct this module error, another redundant module must be added. Let us assume that 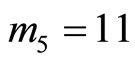 for this requirement in the above residue representation.
for this requirement in the above residue representation.
The current redundant moduli set is
 and the correct residue representation is
and the correct residue representation is
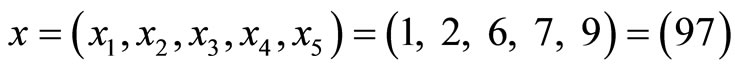 . Let us assume that
. Let us assume that 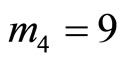 and
and 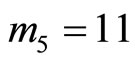 are the redundant moduli. With a single error
are the redundant moduli. With a single error
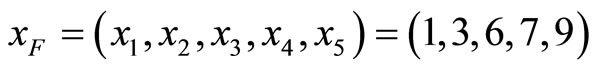 . The TRD theorem can again be used to locate and correct this error. We find that final TRD’s for
. The TRD theorem can again be used to locate and correct this error. We find that final TRD’s for 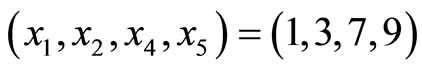 dose not fall in the legitimate range, but other final TRD’s for
dose not fall in the legitimate range, but other final TRD’s for 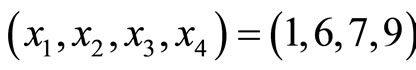 do, falls in the legitimate range:
do, falls in the legitimate range:
1) TRD for  and
and 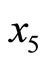
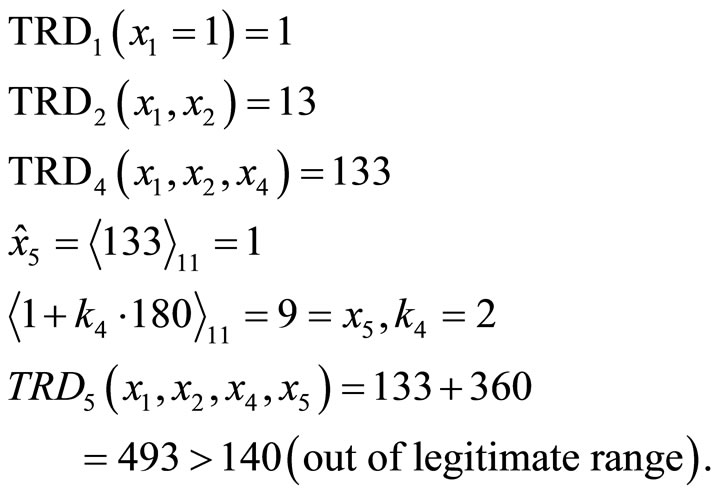
2) TRD for 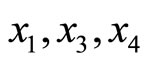 and
and 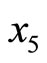

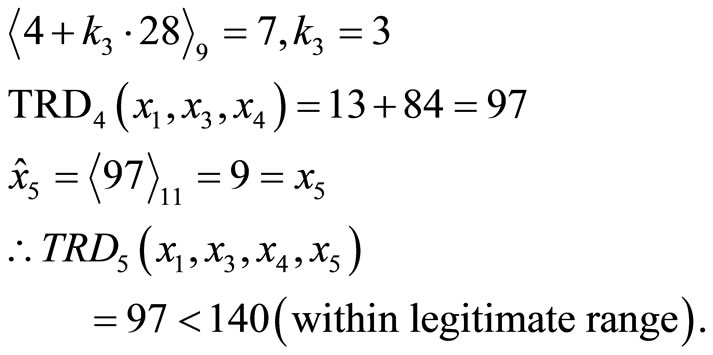
Thus, the error is located at module m2 and must be corrected to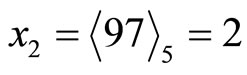 .This algorithm can also be used for multiple error corrections. However, at least three redundant moduli are required. The procedures are similar.
.This algorithm can also be used for multiple error corrections. However, at least three redundant moduli are required. The procedures are similar.
4. Scaling with Error Correction
The above proposed algorithm used for error detection and correction has the advantage of not requiring lookup tables. No CRT (Chinese residue theorem) decoding processes are required. However, it is still time consuming and requires extensive hardware complexity for each module having multiple-value inputs to the match unit and selecting a correct one as a output. To improve this drawback, an optimal matching algorithm is proposed here for the error correction. The following two theorems will be used and an example follows.
Theorem 5. Let m1 and m2 be two relative prime numbers in RNS for module 1 and module 2 respectively. Then there must exist the relation represented by the equation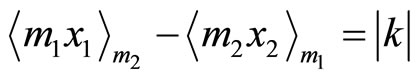 , where
, where
 so that
so that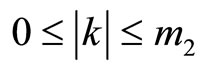 , assuming
, assuming . The
. The 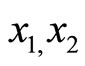 and k are restricted to integers.
and k are restricted to integers.
Proof: As a first step, let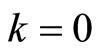 . It is easily seen that
. It is easily seen that 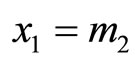 and
and 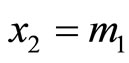 will be satisfied. Next consider
will be satisfied. Next consider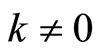 . Since there are two different pair combination
. Since there are two different pair combination
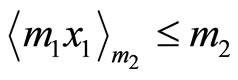 and
and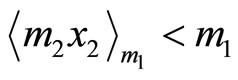 , thus the difference between
, thus the difference between 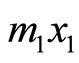 and
and 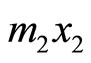 of k will always be satisfied for
of k will always be satisfied for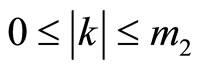 , where k is restricted in integers.
, where k is restricted in integers.
Theorem 6. If the values of m1 and m2 and k in the equation  are known, then p1
are known, then p1
and p2 can always be determined from equation
 or
or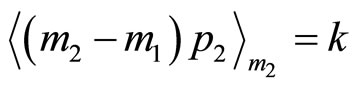 , where p1p2 and k are within the range:
, where p1p2 and k are within the range: 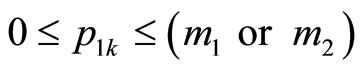
Proof: Let the difference value of  be equal to d, then d will be the integers within the range between 0 and m2, i.e.,
be equal to d, then d will be the integers within the range between 0 and m2, i.e., 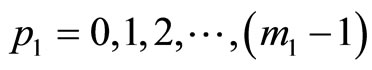 , or
, or
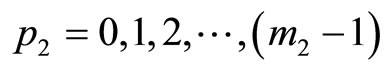 . These two expressions show that we can always select an integer value p, within the interval between 0 and
. These two expressions show that we can always select an integer value p, within the interval between 0 and  or
or 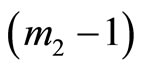 to satisfy the conditions
to satisfy the conditions 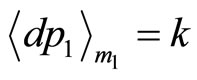 or
or 
Example 4-1 Let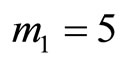 , and
, and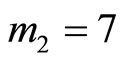 . Find the minimum values of p1 and p2 respectively from the following equation :
. Find the minimum values of p1 and p2 respectively from the following equation :
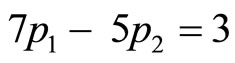
Since 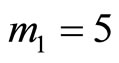 and
and , we have
, we have
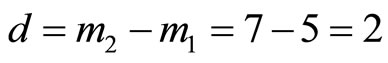 and
and
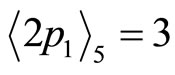 (4-1)
(4-1)
or
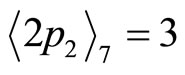 (4-2)
(4-2)
from Equation (4-1)
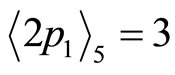 so
so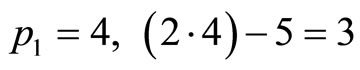
from Equation (4-2)
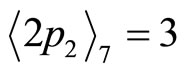 , so
, so .
.
This result can be verified by substituting
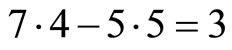 into the above equation. Theorem 6 is very useful as shown in the following example.
into the above equation. Theorem 6 is very useful as shown in the following example.
In Theorem 3 of Section III, the number of cycles on track  from the starting point “0” to its target position “
from the starting point “0” to its target position “ ” can be expressed by setting
” can be expressed by setting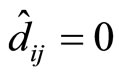 , i.e.
, i.e.
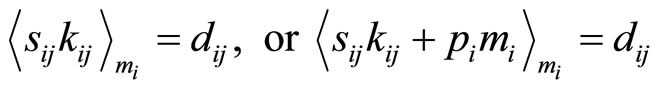 (4-3)
(4-3)
where 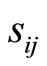 is the module i stride distance referring to module j. Similarly, the number of cycles on track
is the module i stride distance referring to module j. Similarly, the number of cycles on track  from the starting point ”0” to its target position “
from the starting point ”0” to its target position “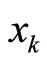 ” can be expressed by setting
” can be expressed by setting , i.e.;
, i.e.;
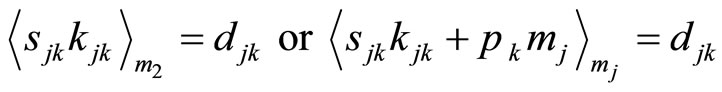 (4-4)
(4-4)
Since, from theorem 3, the cyclic length of the residue digits differences reference to module mj is constant (uniform), then there must exist a condition,
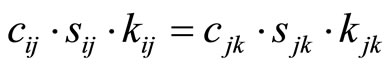 Eliminating the above terms from Equations (4-3) and (4-4),
Eliminating the above terms from Equations (4-3) and (4-4),

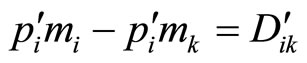
where ,
,  and
and
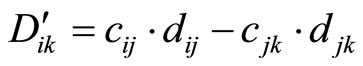
Example 4-2 Let the moduli set 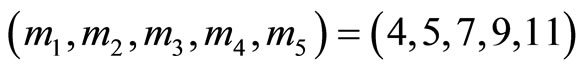
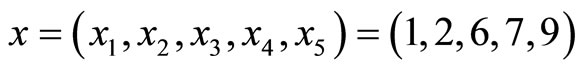 , and the error
, and the error
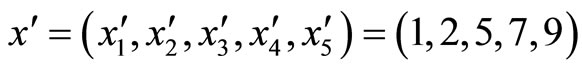 , the error occurs at m3.
, the error occurs at m3.
Follow the same procedures of the Example 4-1 to use this algorithm.
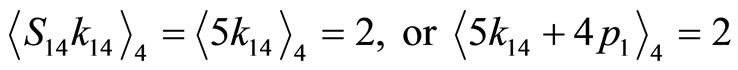 (4-5)
(4-5)
 (4-6)
(4-6)
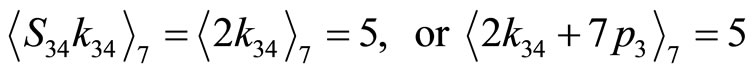 (4-7)
(4-7)
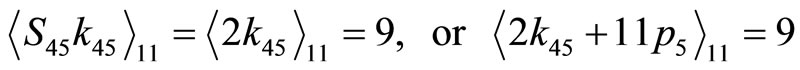 (4-8)
(4-8)
Eliminating 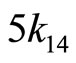 and
and  from Equation’s (4-5) and (4-6)
from Equation’s (4-5) and (4-6)
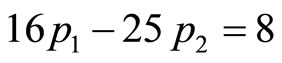 ,
,
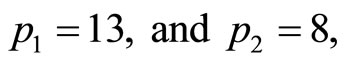
solve for 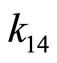 from (4-5),
from (4-5),



or 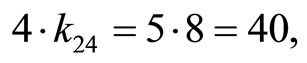
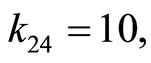
 .
.
Check from Equation (4-5),

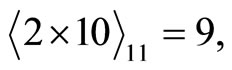
This shows that the error occurs at module m3. From this result, we can immediately obtain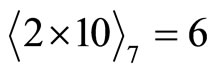 . Noting that it may happen that the assigned referenced memory moduli falls coincidentally with error memory module m3. In this occurrence, we cannot find the correct (integers) values of P1 and P2 within the legitimate range. It seems that this algorithm can only detect error. To complete the error correction procedure, we can simply change the referenced module to any other and follow the same procedure as before. This guarantees that the proposed algorithm in Theorem 4 will also work well in this case. The hardware structure for illustrating this algorithm is shown in Figure 3.
. Noting that it may happen that the assigned referenced memory moduli falls coincidentally with error memory module m3. In this occurrence, we cannot find the correct (integers) values of P1 and P2 within the legitimate range. It seems that this algorithm can only detect error. To complete the error correction procedure, we can simply change the referenced module to any other and follow the same procedure as before. This guarantees that the proposed algorithm in Theorem 4 will also work well in this case. The hardware structure for illustrating this algorithm is shown in Figure 3.
The proposed TRD (target Race Distance) scheme used for error correction can be used for scaling and assigning numbers in a residue number system. A redundant residue number system (RRNS) is defined as before in an RNS with r additional moduli. The moduli
 , are called the nonredundant moduli, while the extra r moduli,
, are called the nonredundant moduli, while the extra r moduli, 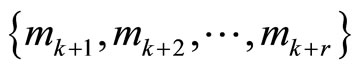 are the redundant moduli. The interval,
are the redundant moduli. The interval,  , is called the legitimate range where
, is called the legitimate range where 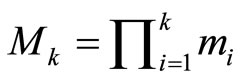 and the interval,
and the interval,  , is the illegitimate range, where
, is the illegitimate range, where 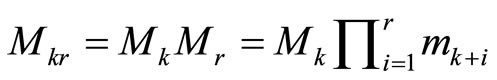 is the total range. In the RRNS, the negative numbers within the dynamic range are represented as states at the upper extreme of the total range, which is part of the illegitimate range. The positive members are mapped to the interval
is the total range. In the RRNS, the negative numbers within the dynamic range are represented as states at the upper extreme of the total range, which is part of the illegitimate range. The positive members are mapped to the interval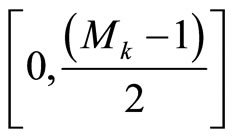 , if Mk is odd, or
, if Mk is odd, or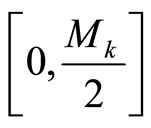 , if Mk is even. The negative numbers are mapped to the interval
, if Mk is even. The negative numbers are mapped to the interval
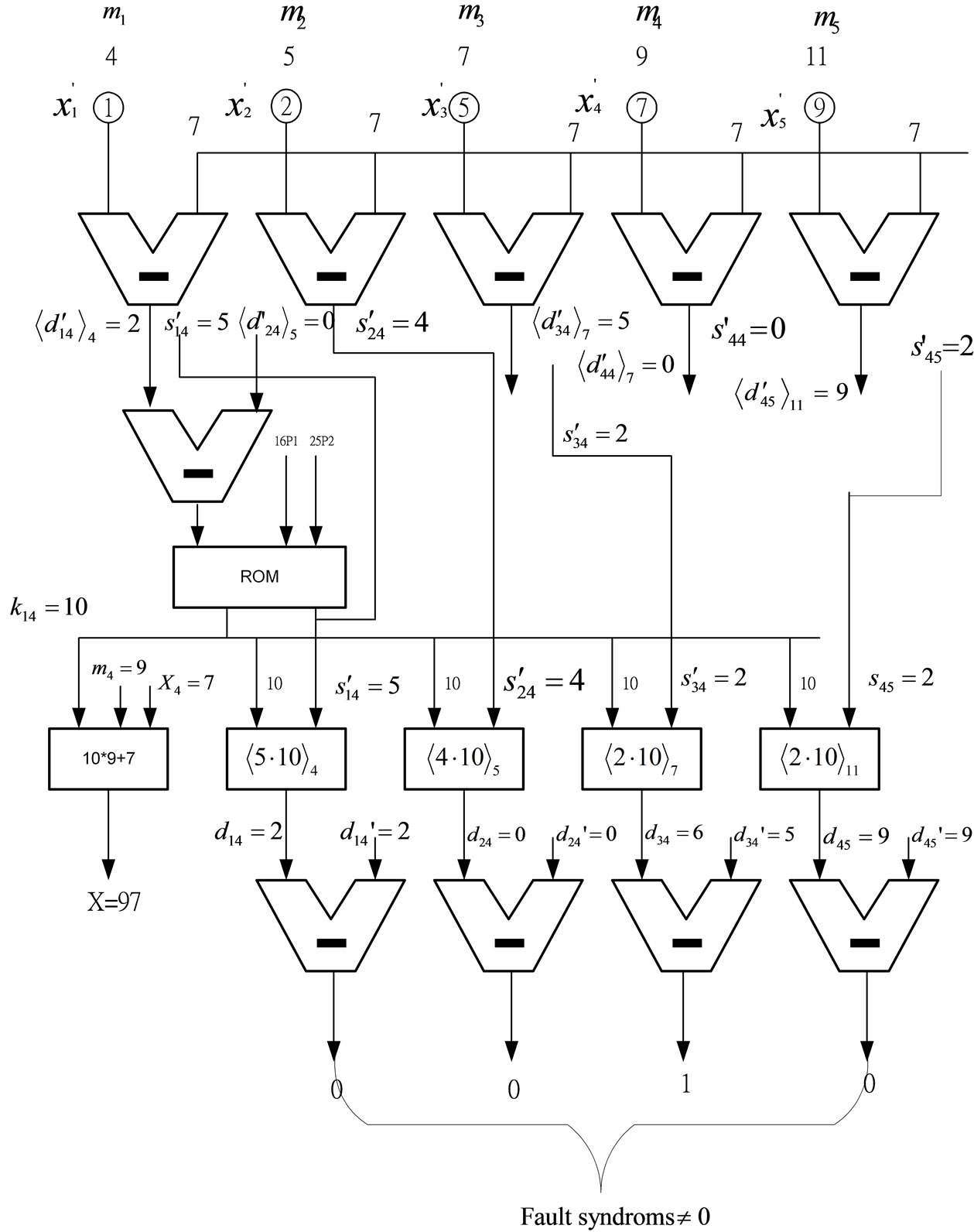
Figure 3. In the block diagram using optimal matching between multiples Pi m and Pkmk, the residue digits are corrected by xi - x4 = di4.
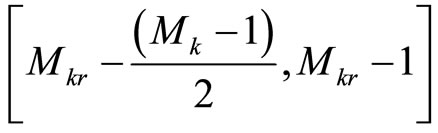 if Mk is odd or
if Mk is odd or
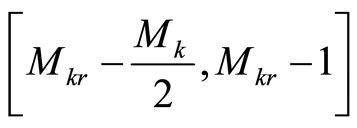 if Mk is even [14].
if Mk is even [14].
The one-to-one correspondence between the integers of the dynamic range and the states of the legitimate range in the RRNS can be established using a polarity shift. [11], The polarity shift is defined as below.
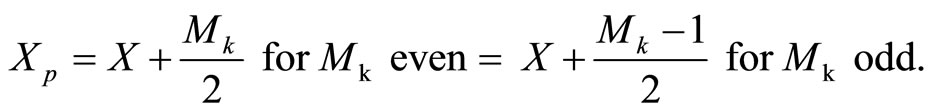
where 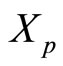 denotes the value X after a polarity shift and
denotes the value X after a polarity shift and
 if
if  is odd, so that
is odd, so that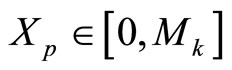 a polarity shift needs to be performed prior to correcting or scaling since
a polarity shift needs to be performed prior to correcting or scaling since 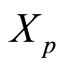 belongs to the legitimate range. If a single residue digit error
belongs to the legitimate range. If a single residue digit error 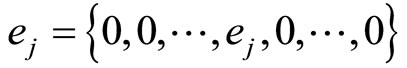 is introduced and corresponds to modules mj, then, after a polarity shift.
is introduced and corresponds to modules mj, then, after a polarity shift.
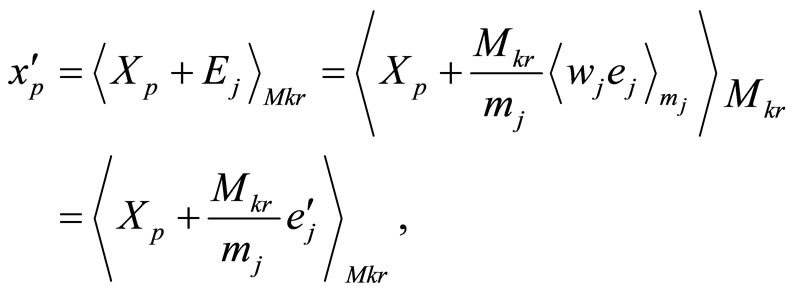
where  is the multiplicative inverse of
is the multiplicative inverse of  moduli mj i.e.
moduli mj i.e. 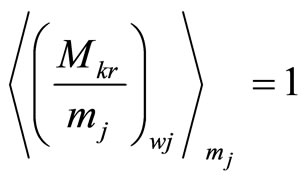 and
and 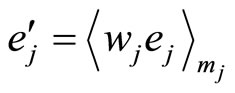 The
The 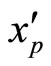
denotes a single residue digit error and must fall within the illegitimate range ,  [11].
[11].
Since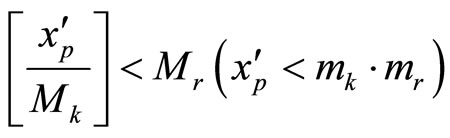 , and can be represented uniquely by
, and can be represented uniquely by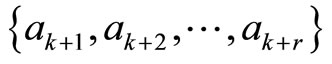 ,where
,where 
are the coefficient from the Chinese Remainder Theorem
(CRT), i.e, 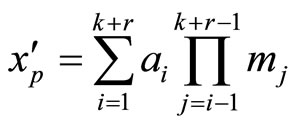 , where
, where . Note that the redundant digits
. Note that the redundant digits  are zeros if no error is introduced, while at least one redundant digit is not equal to zero if a single error is introduced. Therefore, it has the same meaning that
are zeros if no error is introduced, while at least one redundant digit is not equal to zero if a single error is introduced. Therefore, it has the same meaning that 
or 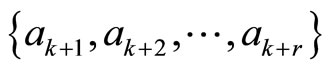 is used to be the entries of the error correction.
is used to be the entries of the error correction.
1) 2)
2) 
Although the errors detection and correction described in section II have been simplified the processes due to no need of CRT conversion. It is still hardware complex and time consuming for the residue scaling operation. To improve this drawback, a direct residue-scaling algorithm can be used. It is flexible and direct to detect and prevent the errors. The flexibility means that the scaling factor can be arbitrary chosen any single module such as , i.e. not necessarily beginning from
, i.e. not necessarily beginning from 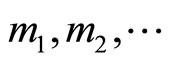 to
to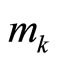 . in order. The direct capability means no requirement for CRT extension processes for decoding or lookup tables. The following theorem (theorem 7) and example are clarified.
. in order. The direct capability means no requirement for CRT extension processes for decoding or lookup tables. The following theorem (theorem 7) and example are clarified.
Theorem 7. If the scaling factor K is one of the module set 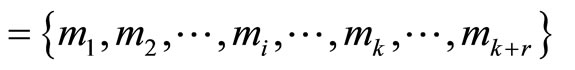 and the residue digits are
and the residue digits are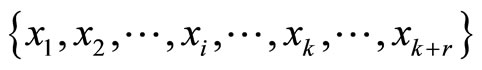 , respectively, then the residue digit
, respectively, then the residue digit  scaled by a factor
scaled by a factor
 can be obtained using the equation
can be obtained using the equation
 (4-9).
(4-9).
Proof: It is easy to show that when , and Equation (4-9) is divided by
, and Equation (4-9) is divided by 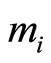 on both side, we have
on both side, we have
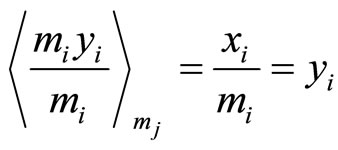 (4-10).
(4-10).
Example 4-3. For convenient comparison of the proposed TRD algorithm to other schemes such as appeared in [14], we take the same numerical example in [11]. Let the moduli set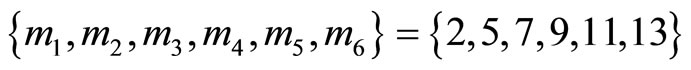 , where
, where 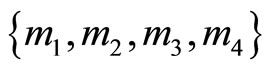 are regular moduli and
are regular moduli and
 are redundant moduli. Then
are redundant moduli. Then
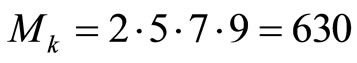 ,
, 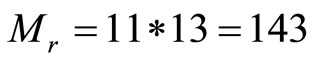 ,
,
 , and
, and
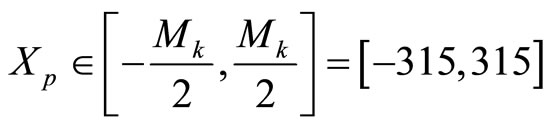 . The sufficient conditions for correcting single residue digits errors are 1)
. The sufficient conditions for correcting single residue digits errors are 1)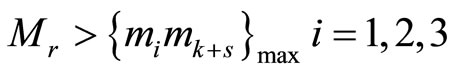 , or 4,
, or 4, 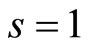 , or 2,
, or 2,
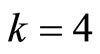 , The maximum
, The maximum
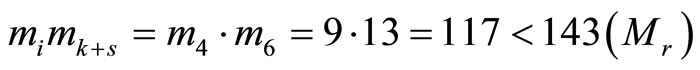 , and 2)
, and 2) 
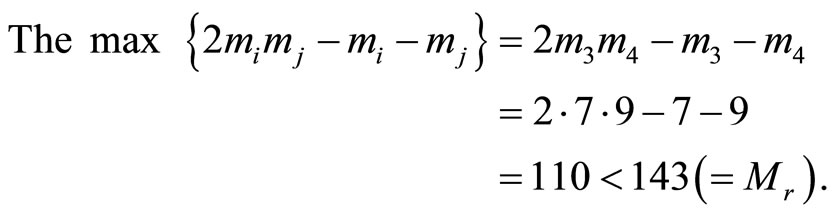
Thus the moduli set satisfies the necessary and sufficient conditions for correcting single errors digit. Assume  and a single digit error
and a single digit error  is introduced, then
is introduced, then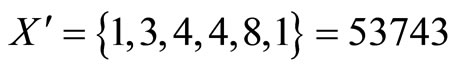 .
.
After a polarity shift, 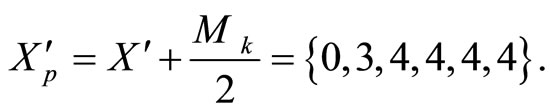
Follow the same procedures as shown in Example 4-2. CPRDD is applied for correction without the need for using a table.
1) Assign the moduli 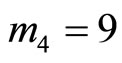 as the reference moduli, the following residue digit references and its corresponding CPRDD equations:
as the reference moduli, the following residue digit references and its corresponding CPRDD equations: 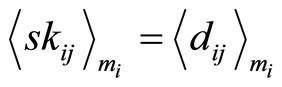 are obtained
are obtained
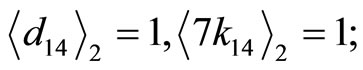
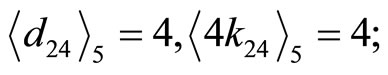
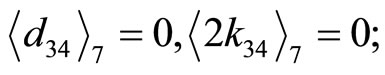
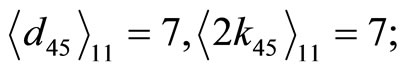
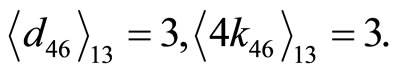
2) Choose two highest digit difference as one pair for equal target race distance e.g.
 . Then the true primary RDD equations are
. Then the true primary RDD equations are
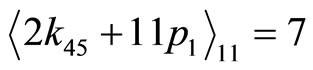 (4-11)
(4-11)
And 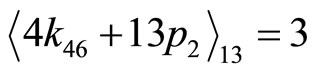 (4-12)
(4-12)
where  and
and 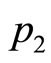 are selected so that the two RDD are equal distances.
are selected so that the two RDD are equal distances.
3) Eliminating k terms in Equation’s (4-11) and (4-12) by putting 
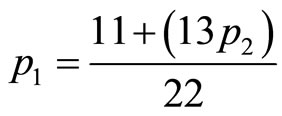
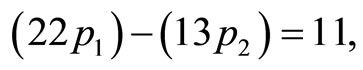 where
where
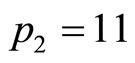 , then
, then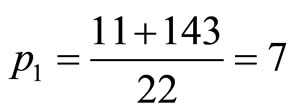 .
.
4) Substituting p1 and p2 into equations (4-9) and (4-10) respectively, we have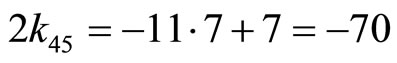 , then
, then
 , and
, and , also,
, also,
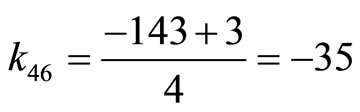 .
.
5) Checking other three RDD’s
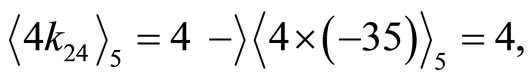
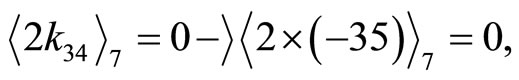
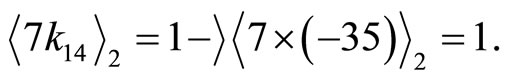
The only different module residue occurs on module number at , i.e.,
, i.e., . The three target distances, can be from any module residue, say, (except
. The three target distances, can be from any module residue, say, (except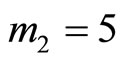 ),
), .
. .
.
The residue representation of X is therefore,
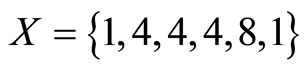 . If a single digit error
. If a single digit error 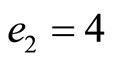 is introduced, then,
is introduced, then,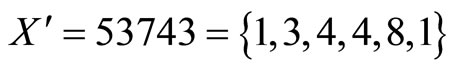 .The corresponding error is therefore
.The corresponding error is therefore
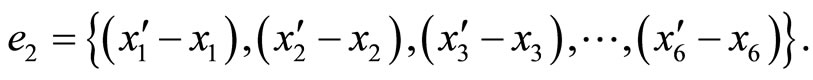
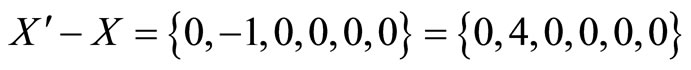

After a polarity shift,
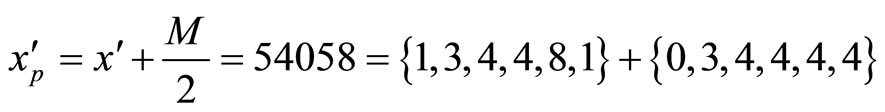
and the scaling factor 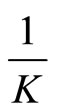 to
to 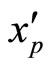 is
is
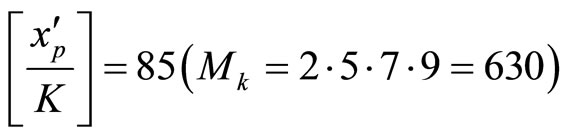 . The final step must use a lookup table to obtain the result,
. The final step must use a lookup table to obtain the result, 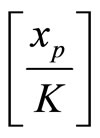 [13].
[13].
For verifying our proposed algorithm, the table of the corresponding 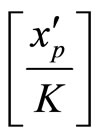 is not required as in [13]. The processes for finding and correcting a single error based on our method are described below.
is not required as in [13]. The processes for finding and correcting a single error based on our method are described below.
1) Find the residue digit difference to a selected module, say  as before
as before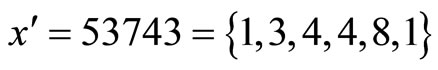 . For verifying that our proposed algorithm detects and corrects single error without using a table, the same numerical example is used to describe the procedure as follows:
. For verifying that our proposed algorithm detects and corrects single error without using a table, the same numerical example is used to describe the procedure as follows:
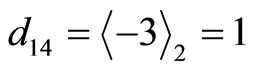 ,
,
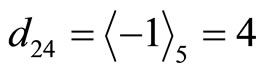 ,
,

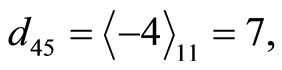
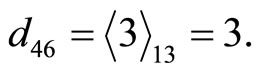
Then
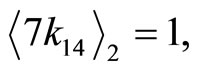

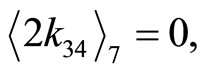

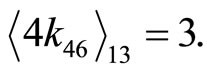
2) Choose two highest digit differences as one pair for equal target race distances. e.g.
 and
and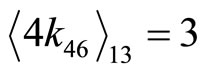 , the following two equations can be obtained:
, the following two equations can be obtained:
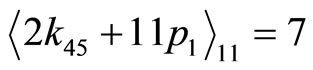 (4-13a)
(4-13a)
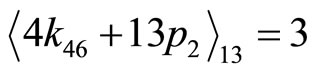 (4-13b)
(4-13b)
3) Eliminating k terms in (4-13a) and (4-13b) by putting 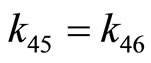
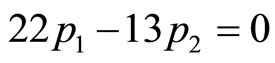 then
then  and
and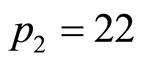 .
.
4) Substituting 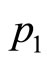 and
and 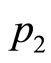 into Equation’s (4-13a) and (4-13b) respectively, we have
into Equation’s (4-13a) and (4-13b) respectively, we have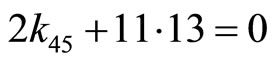 , then
, then , and
, and , also,
, also,


Obviously, the error is located at 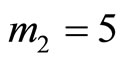 thus
thus
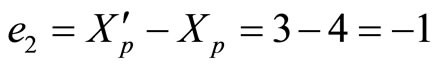 .
.
Furthermore, the CPRDD algorithm can be used directly and in parallel for residue scaling and error correction. Thus the process is greatly speeded up.
Example 4-4 For convenient comparison, the same numeric example as in [13] is illustrated here. Consider , and scaling factor
, and scaling factor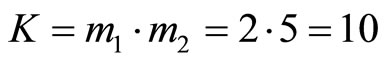 . If an input
. If an input
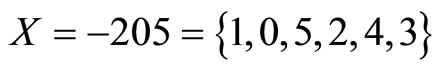 and a single residue digit error
and a single residue digit error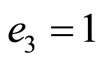 , corresponding to
, corresponding to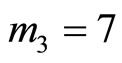 Then
Then 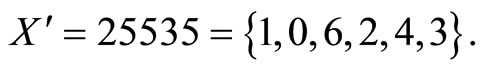
After a polarity shift,
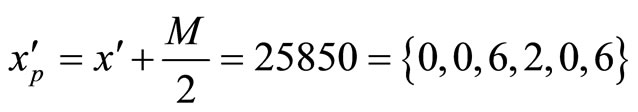
1) Dividing by 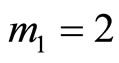 after subtracting
after subtracting 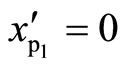 from
from 
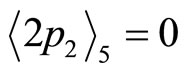 , this leads
, this leads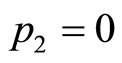 ,
,
 ,
,
 ,
,
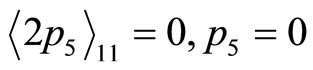 ,
,
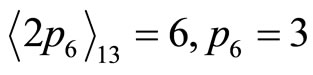 .
.
2) Dividing by 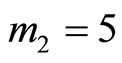 after subtracting
after subtracting
 from
from 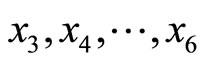
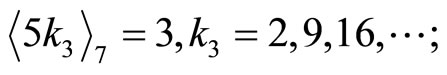
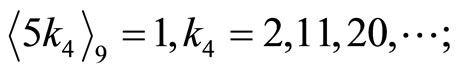
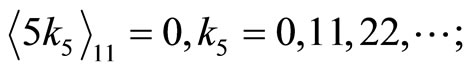
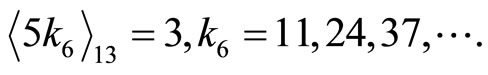
Since from above only k3 does not match with all other’s ki, i.e.  and
and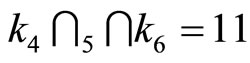 . Therefore, there occurs an error at
. Therefore, there occurs an error at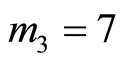 . Once this error is detected, it is easily found and corrected from the above equations,
. Once this error is detected, it is easily found and corrected from the above equations, 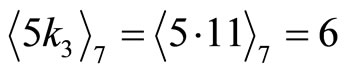 , which in turn
, which in turn
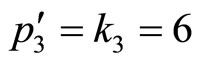 and
and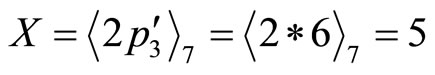 .
.

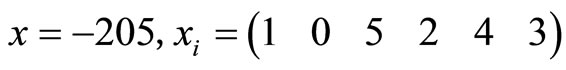
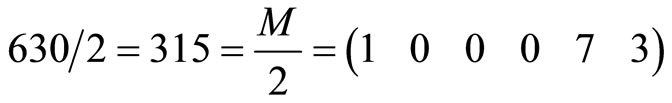
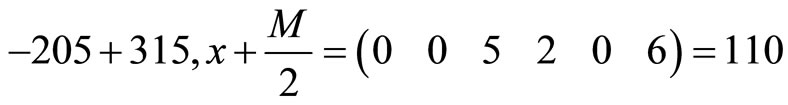
that 
Divided by “2”,

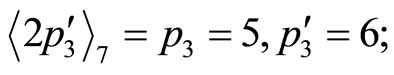
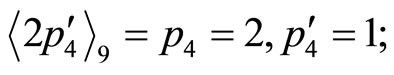
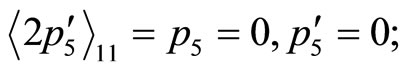
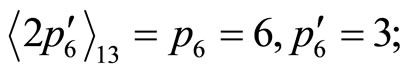
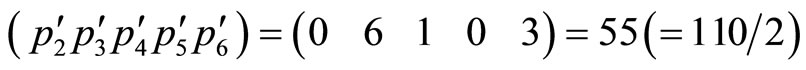 .
.
Divided by “5”
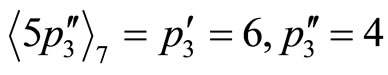 ;
;
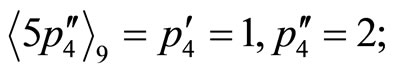


 .
.
The hardware structure of this example for the residue scaling is shown in Figure 4.
Actually this algorithm can be divided by any arbitrary moduli.
Example 4-5 Divided by any arbitrary moduli, say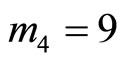 , it must subtract
, it must subtract  from X
from X

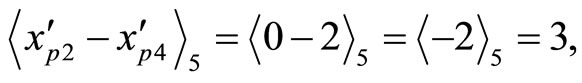
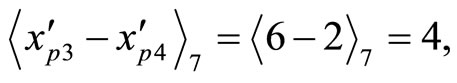

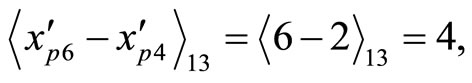
Then

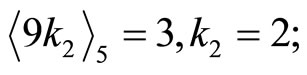
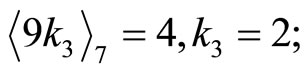
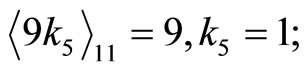

check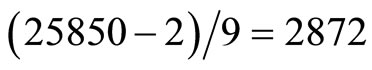 .
.
This results
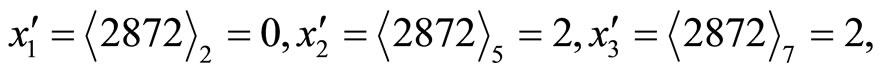

It can be seen from above that
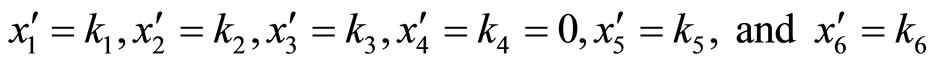 which are equal each other as expected.
which are equal each other as expected.
Example 4-6 For processing two residue scalings and error corrections in parallel, we take Example 4-4 as an illustration. Let scaling factor , i.e., the first residue scaling factor is 2 and the second one is 5 or verse versa. It is easily shown that the extended CPRDD algorithm is used and can be completed in one cycle. That is
, i.e., the first residue scaling factor is 2 and the second one is 5 or verse versa. It is easily shown that the extended CPRDD algorithm is used and can be completed in one cycle. That is



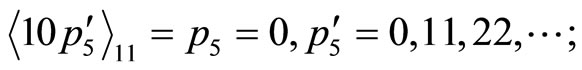
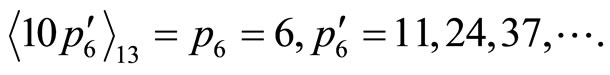
The result is identical
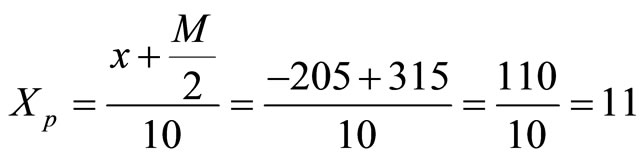 , i.e.,
, i.e.,
 , and
, and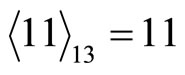 , which are identical results as shown in Example 4-4.
, which are identical results as shown in Example 4-4.
Example 4-7 For error correction



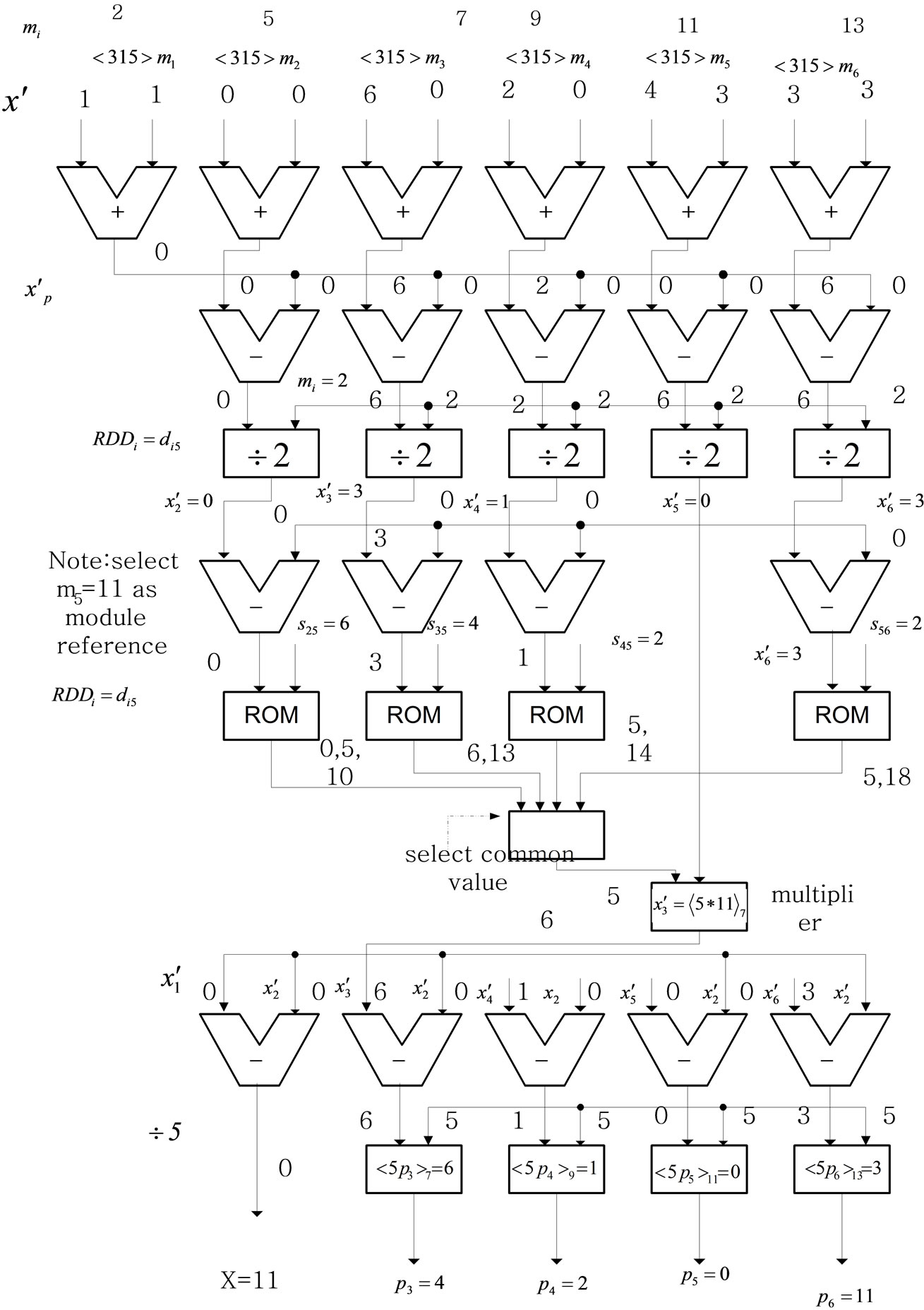
Figure 4. Hardware structure of the residue scaling number for Example 4-4.
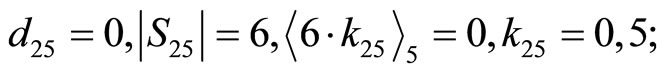



the correct 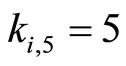

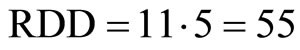 , and
, and

This shows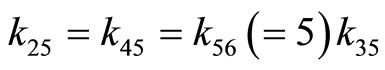 . Therefore the error correction is made by
. Therefore the error correction is made by 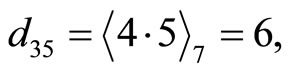 and
and
 , which corresponds to the value in Example 4-4, in scaling factor
, which corresponds to the value in Example 4-4, in scaling factor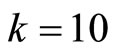 , (dividing by “5” part).
, (dividing by “5” part).
From above results, this checks that scaling
 which is within the accuracy of the residue scaling factor.
which is within the accuracy of the residue scaling factor.
In a general case, 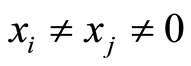 , this time we must modify the subtraction of
, this time we must modify the subtraction of 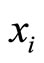 and
and 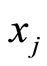 from the X, before the process of the scaling. If
from the X, before the process of the scaling. If 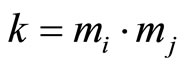 is the scaling factor, then the subtraction must change to
is the scaling factor, then the subtraction must change to
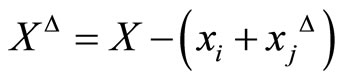 , where
, where  so that
so that
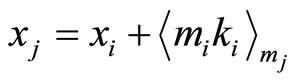 or
or 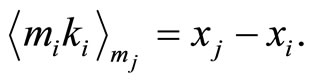 Let us consider the following example:
Let us consider the following example:
Example 4-8
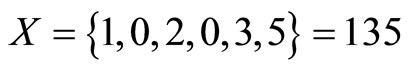 of moduli set
of moduli set
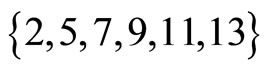 . The scaling factor
. The scaling factor
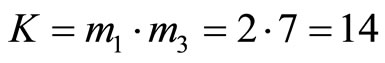 . is assumed. Then, residue
. is assumed. Then, residue
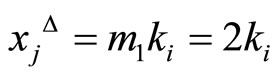 , and
, and 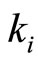 can be found from
can be found from
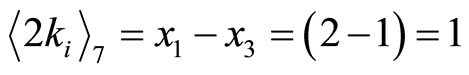 .
.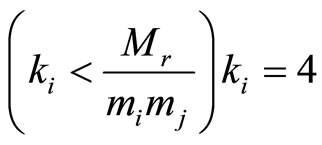 . Thus
. Thus
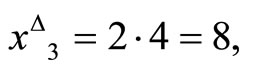 and
and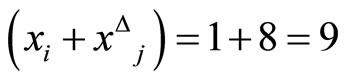 .
.
Alternatively, it could be from other module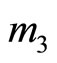 ,
,  , where
, where
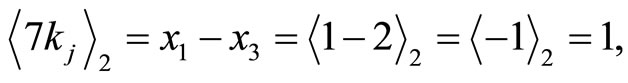 and
and
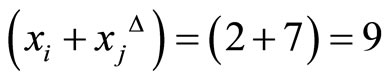

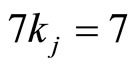 which has the same number to be subtracted.
which has the same number to be subtracted.


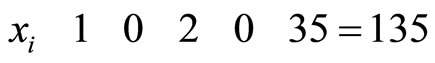


From CPRDD algorithm, the scaling processes are performed as before, we then have the following results by scaling factor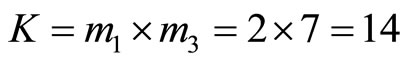 ;
;
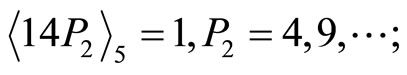
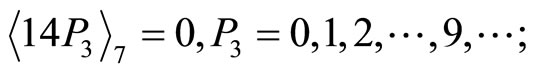
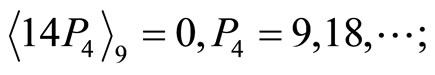
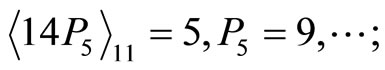

Thus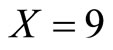 , which is exactly the value
, which is exactly the value 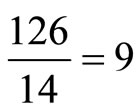 and is the most closed to
and is the most closed to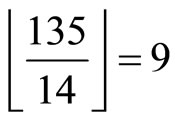 .
.
This result can be checked using sequential steps as follows:
For 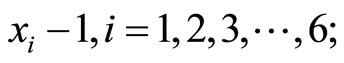
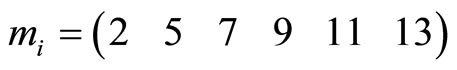
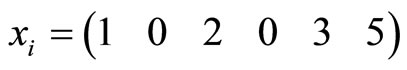
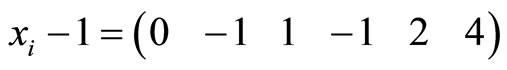
Divided by 2:
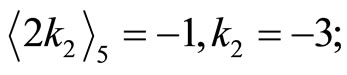
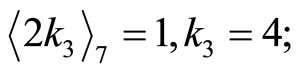

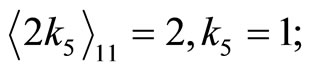
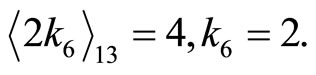
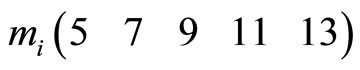
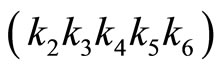
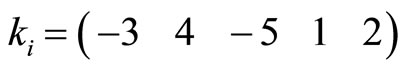

30 0 811 Divided by 7:
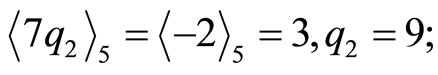
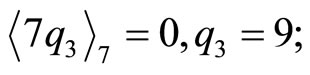
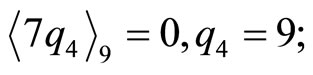
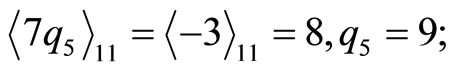
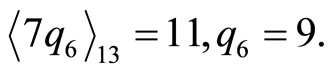
This result of 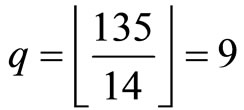 shows that the CPRDD algorithm has the capability of parallel processing operations in residue scaling and error corrections, i.e., any combination moduli scaling factors for Ks of moduli set {m1, m2,
shows that the CPRDD algorithm has the capability of parallel processing operations in residue scaling and error corrections, i.e., any combination moduli scaling factors for Ks of moduli set {m1, m2,  , mk} can be performed simultaneously.
, mk} can be performed simultaneously.
5. Conclusions
The arithmetic operations in the residue number system for addition, subtraction, and multiplication can be speeded up by using its parallel processing properties. However, some difficult operations, such as error detection and correction, must go through conversion or decoding processes from the residue representation to the regional binary number x. This is because the decoding technique is usually accomplished using the mixed-radix digit (MRD) or Chinese Remained Theorem (CRT), which are time consuming processes requiring hardware complexity. We proposed two algorithms for scaling and error correction without the need for lookup tables or increasing the encoding process.
The Cyclic property of the Residue-Digit Difference (CPRDD) algorithm can detect and correct errors from the RNS cyclic property. Any residue moduli set has a specific cycle length, which can be obtained from the individual residue number, difference, each pair, to a reference memory module mi. Once the cyclic length is known, then the original value x is easily found, and in turn, the errors can be detected and corrected.
The TRD (Target Race Distance) algorithm combined with CPRDD is used for scaling and for error detection and correction. The scaling results and error correction can be directly performed by these two algorithms without using MRD or CRT. Thus, the decoding process is significantly reduced, and the hardware structure is greatly simplified. Several examples are illustrated and verified for these two algorithms.
REFERENCES
- R. W. Watson, “Error Detection and Correction and Other Residue-Interacting Operations in a Redundant Residue Number System,” University of California, Berkeley, 1965.
- R. W. Watson and C. W. Hastings, “Self-Checked Computation Using Residue Arithmetic,” Proceedings of the IEEE, Vol. 54, No. 12, 1966, pp. 1920-1931. http://dx.doi.org/10.1109/PROC.1966.5275
- S. S. S. Yau and Y. C. Liu, “Error Correction in Redundant Residue Number Systems,” IEEE Transactions on Computers, Vol. C-22, No. 1, 1973, pp. 5-11. http://dx.doi.org/10.1109/T-C.1973.223594
- D. Mandelbaum, “Error Correction in Residue Arithmetic,” IEEE Transactions on Computers, Vol. C-21, No. 6, 1972, pp. 538-545.
- F. Barsi and P. Maestrini, “Error Correcting Properties of Redundant Residue Number Systems,” IEEE Transactions on Computers, Vol. 22, No. 3, 1973, pp. 307-315. http://dx.doi.org/10.1109/T-C.1973.223711
- F. Barsi and P. Maestrini, “Error Detection and Correction by Product Codes in Residue Number Systems,” IEEE Transactions on Computers, Vol. 23, No, 9, 1974, pp. 915-924. http://dx.doi.org/10.1109/T-C.1974.224055
- V. Ramachandran, “Single Residue Error Correction in Residue Number Systems,” IEEE Transactions on Computers, Vol. C-32, No. 5, 1983, pp. 504-507. http://dx.doi.org/10.1109/TC.1983.1676264
- W. K. Lenkins and E. J. Altman, “Self-Checking Properties of Residue Number Error Checkers Based on Mixed Radix Conversion,” IEEE Transactions on Circuits and Systems, Vol. 35, No. 2, 1988, pp. 159-167. http://dx.doi.org/10.1109/31.1717
- W. K. Lenkins, “Residue Number System Error Checking Using Expanded Projection,” Electronics Letters, Vol. 18, No. 21, 1982, pp. 927-928. http://dx.doi.org/10.1049/el:19820632
- W. K. Lenkins, “The Design of Error Checkers for SelfChecking Residue Number Arithmetic,” IEEE Transactions on Computers, Vol. C-32, No. 4, 1983, pp. 388-396. http://dx.doi.org/10.1109/TC.1983.1676240
- M. H. Etzel and W. K. Jenkins, “Redundant Residue Number Systems for Error Detection and Correction in Digital Filters,” IEEE Transactions on Acoustics Speech and Signal Processing, Vol. 28, No. 10, 1980, pp. 588- 544.
- C. C. Su and H. Y. Lo, “An Algorithm for Scaling and Single Residue Error Correction in Residue Number Systems,” IEEE Transactions on Computers, Vol. 39, No. 8, 1990, pp.1053-1064. http://dx.doi.org/10.1109/12.57044
- H. Y. Lo, “An Optimal Matched and Parallel MixedRadix Converter,” Journal of Information Science and Engineering, Vol. 10, 1994, pp. 411-421.
- A. P. Shenoy and R. Kumaresan, “Fast Base Extension Using a Redundant Modus in RNS,” IEEE Transactions on Computers, Vol. 38, No. 2, 1989, pp. 152-161. http://dx.doi.org/10.1109/12.16508
- E. D. Diclaudis, G. Orlandi and F, Piazza, “A Systolic Redundant Residue Arithmetic Error Correction Circuit,” IEEE Transactions on Computers, Vol. 42, No. 4, 1993, pp. 427-433. http://dx.doi.org/10.1109/12.214689
- S. S. Wang and M. Y. Shau, “Single Residue Error correction Based on K-Term Mj-Projection,” IEEE Transactions on Computers, Vol. 44, No. 1, 1995, pp. 129-131. http://dx.doi.org/10.1109/12.368003
- R. S. Katti, “A New Residue Arithmetic Error Correction Scheme,” IEEE Transactions on Computers, Vol. 45, No. 1, 1996, pp. 13-19. http://dx.doi.org/10.1109/12.481482

