Wireless Engineering and Technology
Vol.1 No.2(2010), Article ID:3031,4 pages DOI:10.4236/wet.2010.12014
Rain Attenuation at Terahertz
![]()
1Department of Communications Engineering, National Defense Academy, Yokosuka, Japan; 2Department of Intelligent Interaction Technology, University of Tsukuba, Tsukuba, Japan.
Email: mizutani@esys.tsukuba.ac.jp
Received July 30th, 2010; revised September 20th, 2010; accepted September 27th, 2010.
Keywords: Rain Attenuation, Raindrop-Size Distribution, Terahertz Waves, P-S Distribution, Weibull Distribution, ITU-R
ABSTRACT
Rain attenuation values were calculated using empirical raindrop-size distributions, which were, Marshall-Palmer (M-P), Best, Polyakova-Shifrin (P-S) and Weibull raindrop-size distributions, and also calculated using a specific rain attenuation model for prediction methods recommended by ITU-R. Measurements of Terahertz wave taken at 313 GHz (0.96 mm) were compared with our calculations. Results showed that the propagation experiment was in very good agreement with a calculation from the specific attenuation model for use in prediction methods by ITU-R.
1. Introduction
Recent advances in electronic and electro-optical Terahertz devices, and improvements in system technology, have stimulated in imaging and sensing applications in the security and non-destructive testing field [1].
Rain attenuation is one of important obstacle to overcome for imaging and sensing system to detect the hazardous things using Terahertz waves above 300 GHz because of its masking action. Raindrop-size distribution has been found to play an important role in monitoring rainfall and in predicting the rain attenuation. The rain attenuation is particularly severe and greatly dependent on various models of raindrop-size distribution in a Millimeter and Terahertz wave system.
2. Raindrop-Size Distribution
Many raindrop-size distributions have been proposed. Marshall and Palmer [2] proposed the following wellknown empirical expression by fitting their data and the Laws and Parsons data. Their data was taken in Ottawa, Canada in 1946 using the filter paper method. The fit of this distribution to the experimental points was not very good for drops less than 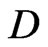 = 1 mm.
= 1 mm.
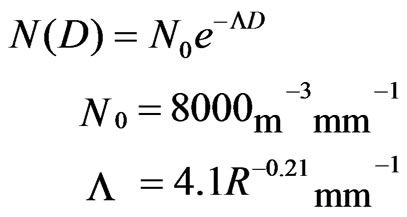 (1)
(1)
where  is the diameter in mm, and
is the diameter in mm, and  is the precipitation rate in mm/hr.
is the precipitation rate in mm/hr.
Best [3] proposed a drop-size distribution model after analyzing a large amount of experimental data in 1950. This is written as
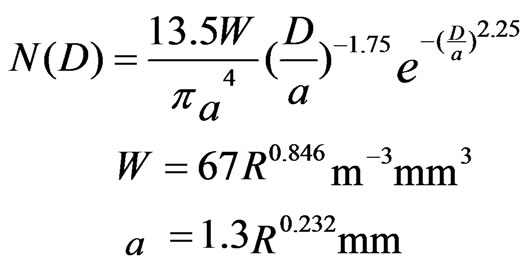 (2)
(2)
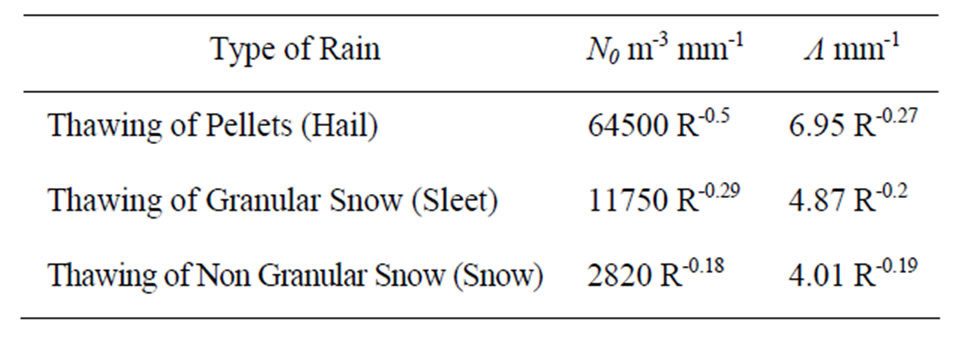
Litovinov proposed a model [4] in 1957 and [5] in 1958 due to Polyakva and Shifrin (P-S) using the Russian data for all three types of rain. This model was also described by Krasyuk, Rozenberg and Chistyakov [6] in 1968 and by University of Tennessee [7] in 1975. It is one case of Gamma distribution proposed by Atlas and Ulbrich [8] in 1984:
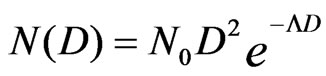 (3)
(3)
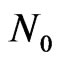 and
and  vary based on the rain types of thawing:
vary based on the rain types of thawing:
Sekine and Lind [9] proposed a Weibull distribution in 1982 by using the FOA data (from the National Defence Research Institute) in Sweden:
 (4)
(4)
This distribution is retained for microwave applications for drizzle, widespread rain, and shower rain cases [10-22].
3. Rain Attenuation
3.1. Calculations
Rain attenuation was calculated by using three types of raindrop-size distributions and a specific attenuation model for use in prediction method recommended by ITU-R.
For calculations using by raindrop-size distributions, rain specific attenuation 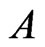 in dB/km is calculated by integrating all of the drop sizes as
in dB/km is calculated by integrating all of the drop sizes as
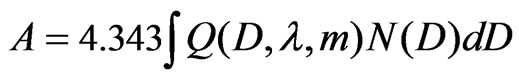 (5)
(5)
where 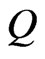 is the attenuation cross section that is a function of the drop diameter
is the attenuation cross section that is a function of the drop diameter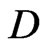 , the wavelength of the radio wave
, the wavelength of the radio wave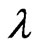 , and the complex refractive index of the water drop
, and the complex refractive index of the water drop , which is a function of the frequency and the temperature, and
, which is a function of the frequency and the temperature, and 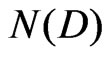 is the drop-size distribution. The attenuation cross section
is the drop-size distribution. The attenuation cross section 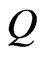 is found by applying the classical scattering theory of Mie for a plane wave radiation to an absorbing sphere particle. According to Hulst [23], the cross section
is found by applying the classical scattering theory of Mie for a plane wave radiation to an absorbing sphere particle. According to Hulst [23], the cross section 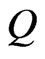 is expanded as
is expanded as
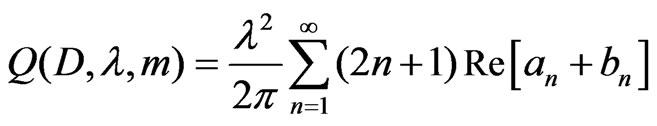 (6)
(6)
where 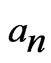 and
and  are the Mie scattering coefficients, which are complex functions of
are the Mie scattering coefficients, which are complex functions of ,
, 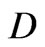 , and
, and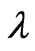 . The complex refractive index of liquid water
. The complex refractive index of liquid water 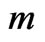 was taken from [24]. The “Mie scattering coefficients”
was taken from [24]. The “Mie scattering coefficients” 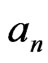 and
and 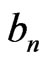 in Equation (6) represent a contribution to the scattered field from the multi poles induced in the sphere, such as raindrops [23].
in Equation (6) represent a contribution to the scattered field from the multi poles induced in the sphere, such as raindrops [23].
For calculation by using the recommended prediction methods by ITU-R [24], rain specific attenuation 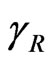 dB/ km is obtained from the rain rate
dB/ km is obtained from the rain rate 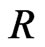 mm/hr using the power-law relationship:
mm/hr using the power-law relationship:
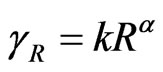 (7)
(7)
Values for the constants for the coefficients 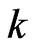 and
and 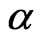 are determined as functions of frequency,
are determined as functions of frequency, 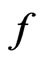 GHz, in the range from 1 to 1000 GHz, from the equations which have been developed from curve-fitting to power-law coefficients derived from scattering calculations. It is shown in ITU-R P.838-3 [25].
GHz, in the range from 1 to 1000 GHz, from the equations which have been developed from curve-fitting to power-law coefficients derived from scattering calculations. It is shown in ITU-R P.838-3 [25].
3.2. Experiments and Computations
Figure 1 shows the results of 313 GHz under a rain fall rate of up to 12 mm/hr. This rain attenuation experiment was carried out by Babkin et al. [26] in the central part of the European part of the former Soviet Union during June and July 1969. The transmitter and receiver were spaced 1 km apart for the measurement.
For the calculations, rain drop-size distributions were used for M-P, Best, P-S and Weibull which were described in Equations (1), (2), (3) and (4) respectively, and specific attenuation model recommended by ITU-R was used for ITU-R which was described in Equation (7). M-P stands for Marshall and Palmer, P-S stands for Polyakva and Shifrin. Best, Weibull and ITU-R used the same name.
An experimental fit curve (shown by the broken line) derived from the raw data with triangular dots was described as A = 1.53 R0.638 [26].
The experimental data obtained from the rain attenuation was shown in Figure 1. It was compared with the calculations of rain attenuations. The departure of the empirical data and the calculated rain attenuations were estimated by calculating the root mean square error (rmse).
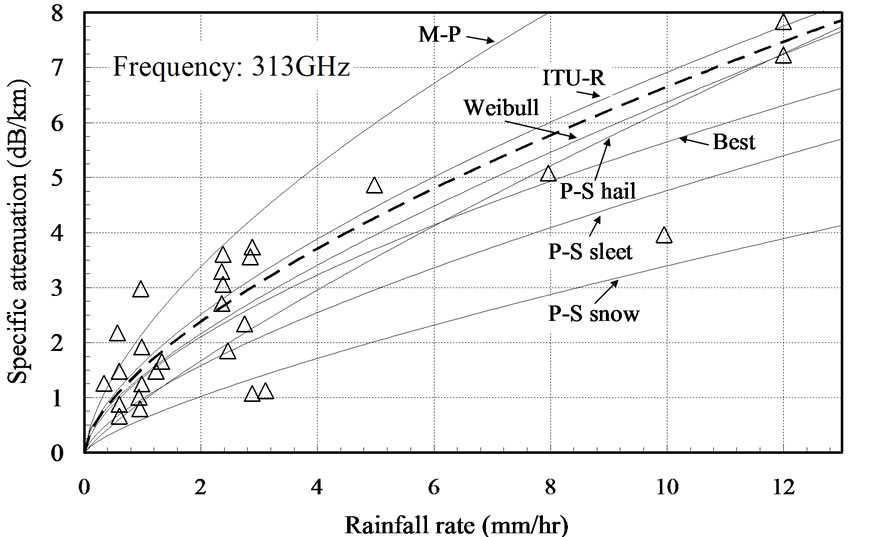
Figure 1. Comparison between calculations and measurements at 313 GHz.

Table 1. Values of rmse for various raindrop attenuations.
These were shown in Table 1. Result showed that the calculation from Weibull and ITU-R were very good agreement with the experimental data. And the best fit was the calculation from ITU-R with the smallest rmse.
4. Conclusions
Rain attenuation at 313 GHz was calculated by using four raindrop-size distributions and using ITU-R specific attenuation model. Calculated results were compared with propagation experiments under a rainfall intensity up to 12 mm/hr. Results showed that the propagation experiment was in very good agreement with the calculation from the specific attenuation model for use in prediction method by ITU-R provided the best fit for the experimental data. Finally, there is greater interest in the rain attenuation at Terahertz waves. An experiment on rain attenuation above 300 GHz at different rainfall rates with various raindrop-size distributions is desirable, especially at a higher rainfall intensity that may cause fatal damage to Terahertz applications.
REFERENCES
- R. M. Langdon, V. Handerek, P. Harrison, H. Eisele, M. Stringer, C. F. Rae and M. H. Dunn, “Military Applications of Terahertz Imaging,” 1st EMRS DTC Technical Conference, Edinburgh, 2004.
- J. S. Marshall and W. M. K. Palmer, “The Distribution of Raindrops with Size,” Journal of Meteorology, Vol. 5, No. 4, 1948, pp. 165-166.
- A. C. Best, “The Size Distribution of Raindrops,” Quarterly Journal of the Royal Meteorological Society, Vol. 76, No. 327, 1950, pp. 16-36.
- I. V. Litovinov, “On the Distribution Function of Particles of Rainfall,” Izvestia AN SSSR, Geophysical Series, No. 6, 1957, pp. 838-839.
- I. V. Litovinov, “Size Distribution of Raindrops from Melting Hail,” Izvestia, Geophysical Series, No. 6, 1958, pp. 903-912.
- N. P. Krasyuk, V. I. Rozenberg and D. A. Chistyakov, “Attenuation and Scattering of Radar Signals by Radio with Shifrin and Marshall-Palmer Drop Size Distributions,” Radio Engineering and Electronic Physics, Vol. 13, No. 10, 1968, pp. 1638-1640.
- “Investigation of Radar Rain Clutter Cancellation Using a Polarization Method,” RADC-TR-75-126, Final Technical Report, University of Tennessee, Knoxville, August 1975.
- C. W. Ulbrich and D. Atlas, “Assessment of the Contribution of Differential Polarrization to Improve Rainfall Measurements,” Radio Science, Vol. 19, No. 1, 1984, pp. 49-57.
- M. Sekine and G. Lind, “Rain Attenuation of Centimeter, Millimeter and Submillimeter Radio Waves,” Proceedings of 12th European Microwave Conference, Helsinki, 1982, pp. 584-589.
- M. Sekine and C. D. Chen, “Rain Attenuation in Terrestrial and Satellite Communications Links,” Proceedings of the 15th European Microwave Conference, Paris, 1985, pp. 985-990.
- C. D. Chen, Y. Okamoto and M. Sekine, “Cancellation of Radar Rain Clutter Using Circular Polarization,” Transactions on IECE of Japan (Section E), Vol. E68, No. 9, 1985, pp. 620-624.
- M. Sekine, “The Relationship between Radar Reflectivity and Rainfall Rate,” Transactions on IECE of Japan (Section E), Vol. E69, No. 5, 1986, pp. 581-582.
- M. Sekine, “Rain Attenuation from Various RaindropSize Distributions,” Transactions on IECE of Japan (Section E), Vol. E69, No. 6, 1986, pp. 711-712.
- M. Sekine, C. D. Chen and T. Musha, “Rain Attenuation from Log-Normal and Weibull Rain-Drop Distributions,” IEEE Transactions on Antennas and Propagation, Vol. AP-35, No. 3, 1987, pp. 358-359.
- M. Sekine, T. Musha and C. D. Chen, “Rain Attenuation from Weibull Raindrop-Size Distribution,” Proceedings of 18th European Microwave Conference, Stockholm, 12-15 September 1988, pp. 423-428.
- M. Sekine and C. D. Chen, ”Inversion Problem in Rain Attenuation Calculations,” Proceedings of the 1989 URSI International Symposium on Electromagnetic Theory, Stockholm, 1989, pp. 23-25.
- H. Jiang, M. Sano and M. Sekine, “Radar Reflectivity and Rainfall Rate Relation from Weibull Rain Drop-Size Distribution,” IEICE Transactions on Communications, Vol. E79-B, No. 6, 1996, pp. 797-800.
- H. Jiang, M. Sano and M. Sekine, “Weibull RaindropSize Distribution and Its Application to Rain Attenuation,” IEE Proc-Microwaves Antennas Propagation, Vol. 144, No. 3, 1997, pp. 197-200.
- S. Sayama and M. Sekine, “Influence of Raindrop-Size Distribution on the Differential Reflectivity up to Submillimeter Wavelength of 0.96 mm,” International Journal of Infrared and Millimeter Waves, Vol. 23, No. 5, 2002, pp. 775-784.
- S. Ishii, “Rain Attenuation at Millimeter Wavelength of 1.33 mm,” International Journal of Infrared and Millimeter Waves, Vol. 25, No. 10, 2004, pp. 1495-1501.
- T. Utsunomiya and M. Sekine, “Rain Attenuation at Millimeter and Submillimeter Wavelength,” International Journal of Infrared and Millimeter Waves, Vol. 26, No. 6, 2005, pp. 905-920.
- T. Utsunomiya and M. Sekine, “Rain Attenuation at 103 GHz in Millimeter Wave Ranges,” International Journal of Infrared and Millimeter Waves, Vol. 26, No. 11, 2005, pp. 1651-1660.
- H. C. Hulst, “Light Scattering by Small Particles,” Wiley, New York, 1957.
- P. S. Ray, “Broad Complex Refractive Indices of Ice and Water,” Applied Optics, Vol. 11, August 1972, pp. 1836- 1844.
- Recommendation, ITU-R P. 838-3, International Telecommunication Union, “Specific Attenuation Model for Rain for Use in Prediction Methods,” 2005.
- Y. S. Babkin, N. N. Zimin, A. O. Izyumov, I. A. Iskhakov, A. V. Sokolov, L. I. Stroganov, Y. V. Sukhonin and G. Y. Shabalin, “Measurement of Attenuation in Rain over 1 km Path at a Wavelength of 0.96 mm,” Radio Engineering and Electronic Physics, Vol. 15, No. 12, 1970, pp. 2164- 2166.

