Wireless Engineering and Technology
Vol.1 No.1(2010), Article ID:2343,5 pages DOI:10.4236/wet.2010.11007
Sensor Placement to Improve the Positioning Performance Based on Angle of Arrival (AOA)
![]()
School of Electrical Engineering, Iran University of Science and Technology, Tehran, Iran.
Email: behzad.omidali@gmail.com, abeheshti@iust.ac.ir
Received March 20th, 2010; revised July 12th, 2010; accepted July 19th, 2010.
Keywords: Sensor placement, positioning, Cramer-Rao bound, numerical optimization
ABSTRACT
In this paper, a method for sensor placement to improve the placement quality based on angle of arrival of signal in a specific area is proposed. The installation place of sensors may be constrained with specified boundaries. In this method, the criterion of maximum quality of placement is the Cramer-Rao bound. The generalized pattern search as an effective method is used to maximize error bound of the placement problem by angle of arrival. Better results are obtained in comparison with results of genetic algorithm. The derived results are compared from two aspects of run time and result quality.
1. Introduction
Positioning based on receiving and processing of radio signals has military, communication, navigation and even biologic application in the today world. Thus, study of positioning quality and methods to improve it has also a considerable importance. In a first glance, many methods are came to mind to improve the quality of positioning, for instance, improving the efficiency of sensors, improving the efficiency of positioning algorithms and proper design for installation location of sensors are some examples of these methods. In this paper, a method for determination of sensor position to improve the positioning quality in a specific area is considered. It is notable that in this paper the sensors are also constrained in the sense of the installation location and their position is not eligible to be in any desired location in the plane.
Yang and Scheuing are analytically and in some special cases prove that to decrease the positioning error in regular ranges such as circle and sphere, the existing sensors must be located on the perimeter of circle or surface of sphere symmetrically [1,2]. The case of study in these papers, is a very special case of sensor placement, because in some cases, all margins of positioning area is not available. In real applications, it is not possible to freely position the sensors and some places are not permitted to be positioned by a sensor; thus, in sensor placement, the location constraints of sensors must be considered.
From another aspect, there are several criterions to define and measure the positioning quality. These criterions might be related to average, maximum or cumulative density function (CDF) of error in the considered area. After defining the quality criterion, a method to calculate it must be proposed. For this aim, a complete simulation of positioning system with a Mont-Carlo method or an approximation of positioning error with existing bounds might be used. In this paper, the criterion of maximum positioning error in the considered area is chosen which is approximated with Cramer-Rao bound and this criterion is minimized with changing place of sensor locations.
After defining the quality criterion, the optimization method for sensor placement must be studied. For this purpose, we arrange all sensor places in an array and employ a cost function to calculate the quality criterion for this array. Then, optimizing the obtained function (minimization of the error or maximization of quality) the problem of sensor placement is solved.
This paper is organized as follows: in Section 2 the positioning problem using angle of arrival is investigated and the Cramer-Rao bound is mentioned for it. In Section 3, the effect of sensor placement on positioning is studied. The proposed method for sensor placement is presented in Section 4. In Section 5, a method based on genetic algorithm as a reference method for comparison is introduced. In Section 6 the results are compared and finally the paper is summarized and concluded in Section 7.
2. The Placement Problem
In this paper, for investigation of proposed sensor placement method, the positioning problem with angle of signal is considered. This type of positioning is efficient in applications in which the sent signal of desired source is a pulse signal.
AOA equations for a source in place of  and N sensors at locations of
and N sensors at locations of 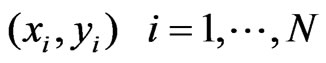 are as follows
are as follows
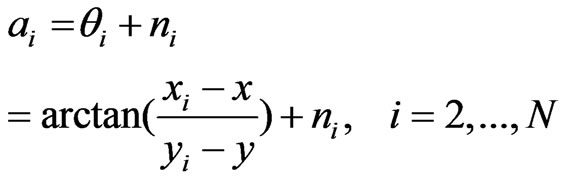 (1)
(1)
where, 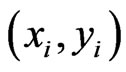 denotes place of ith sensor and ni s are uncorrelated Gaussian noise with covariance matrix of
denotes place of ith sensor and ni s are uncorrelated Gaussian noise with covariance matrix of
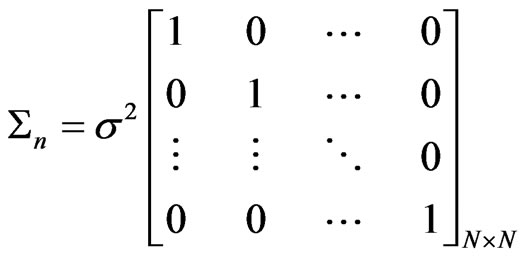 (2)
(2)
Cramer-Rao lower bound is obtained for positioning using AOA as follows [3]
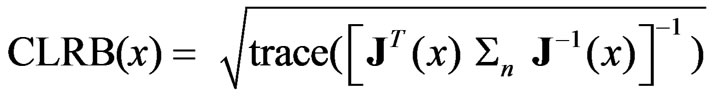 (3)
(3)
where, operations of ,
,  ,
,  and
and  are square root, summation of main diagonal of matrix, transpose of matrix and matrix inverse operation. Furthermore
are square root, summation of main diagonal of matrix, transpose of matrix and matrix inverse operation. Furthermore 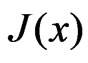 is Jacobean matrix of noiseless angle with respect to target position, which is defined as
is Jacobean matrix of noiseless angle with respect to target position, which is defined as
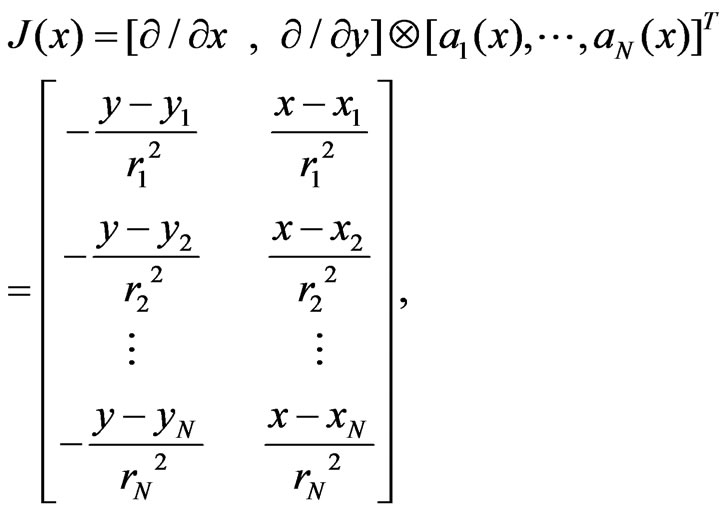 (4)
(4)
where, 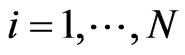 and
and 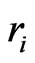 is distance between target to ith sensor. Moreover, operations of
is distance between target to ith sensor. Moreover, operations of ,
,  and
and  shows derivation respect x, y and Kronecker product operation.
shows derivation respect x, y and Kronecker product operation.
The Cramer-Rao lower bound is achievable when position of target respect to position of sensor is not inappropriate. For example, the Gauss-Newton [4] method if it is converged, the error reaches to Cramer-Rao lower bound. Positioning methods such as factor graph [5] or Levenberg –Marquardt [6] have better convergence and reach to Cramer-Rao lower bound. So, this bound is appropriate approximation for showing positioning error in practical systems.
3. Effects of Sensor Placement
To investigate the effect and importance of sensor placement in positioning, a supposed scenario is considered. Figure 1 shows the lower bound of Cramer-Rao error for the specified area in upper half-plane with symmetrical sensor placement in lower half-plane. Standard deviation of error in angle of arrival recognition of signal in each sensor is supposed to be 50 meter. In Figure 1, the right bar, shows the amount of error in each point proportional to the color of that point on the screen.
For optimization in this case, the maximum of positioning error in each area which is the positioning quality index, will be calculated. In Figure 2 this index is minimized and the sensors are replaced to minimize the maximum of positioning error in the considered area. In this case, also it is assumed that the sensors are constrained to place in lower half-plane.

Figure 1. Crammer-Rao error for highlighted region with symmetric positioning of sensors on a rectangular

Figure 2. Crammer-Rao error for highlighted region with symmetric positioning of sensors in a way that maximum positioning error is minimized in the proposed region
For the first case, in which the best symmetrical arrangement is chosen, the maximum error is 815.3 meters, while with optimal placement of sensors this error decreases to 766.1 meters which is an improvement of 6.05%. In practical applications, the requirements of federal communication commission considers a standard for the error which says that in the 65% of considered area the positioning error must be lower than 100 meters or in 95% of mentioned area the error must be lower than 300 meters. Considering maximum error index in an area means that in 100% of that area, the positioning error is lower than determined limit. Note that this design and calculation of maximum positioning error index using the approximation of Cramer-Rao bound is a theoretical process, thus, if in an area, the positioning error in 100% of the points is lower than a determined amount, this will guarantee a certainty margin of 5% to satisfy the standard index of 95%.
The numerical method to calculate the cost function or the maximum positioning error in an area is using a grid of points inside the supposed area. In this method, for all points of this grid, the positioning error bound is calculated, and then these values in all points are compared and their maximums are chosen as the numerical amount of criterian. The numerical method of optimization, which will be considered in Section 4, minimizes this index by replacing the position of sensors. In this paper, to accelerate the calculation of cost function a grid of 40 × 40 points is employed, but the final results are reported using a grid of 200 × 200 points.
4. Propose Method for Sensor Placement
The proposed method to minimize the cost function is using generalized pattern search which will be described in brief. Respect to the comparison of next section, this method is less complex from two aspects of realization and efficiency compared with genetic algorithm; thus this method is a proper method for sensor placement which this application of the method has not been reported in literature, since now.
Generalized pattern search is method for numerical minimization of functions without the need for gradient or other derivatives of functions. In this method, with a start point for the position of sensor and using a series of specified patterns to replace the sensors and with a search radius, the enamoring points of initial one are investigated and in the case of finding a better point, the position of sensor is transferred to that point and the search is continued with applying an expansion factor and with a larger search radius. The number of used patterns in each stage is four times of the number of sensors means that each action of increase or decrease in latitude or longitude coordinates of each sensor is considered as a pattern. In this method, if a better point is not found, the search radius is decreased applying a condensation factor and the search stages are repeated. It is not easy to prove that there is no local minimum for a numerical problem such as our positioning problem, but respect to the simulation results, with a high certainty, there is no local minimum in this problem.
Although it is not necessary, to certify that the initial point is not too improper and the convergence happens with acceptable rate, we can use the best member of a random small population as the initial point. Table 1 shows the parameters used in the generalized pattern search. Respect to table 1, the condensation factor of search radius is 1/4, while the expansion factor of search radius is 2. The default values are generally 1/2 and 2, but in this problem, for an accelerated convergence and converges to a precise solution in lower number of iterations.
5. Method Based on Genetic Algorithm
To optimize the defined cost function, genetic algorithm, as a strong numerical optimization method, can be employed. However, using genetic algorithm considerably increases the possibility to escape the local minimums [7, 8]. But for this certainty, a heavier calculation load is imposed compared with the proposed method. Note that, in genetic algorithm the selected values for parameters of algorithm must be proper. In this paper, due to the lack of references for the use of genetic algorithm in sensor placement, these parameters are selected via try and error method in some experiments.
Several genetic algorithm parameters which are used in this paper are provided in Table 2.
For the fraction of next generation which is born by crossover, the typical value is 0.8 and the values between 0.4 and 0.8 are acceptable. In this problem the value of 0.5 is selected with an aim to have more new members in each generation and thus a larger search area for the algorithm. Based on the performed simulations for parent selection function, competition method [7] has less final error respect to roulette wheel [8] and other methods and therefore is considered in simulations. Adaptive mutation
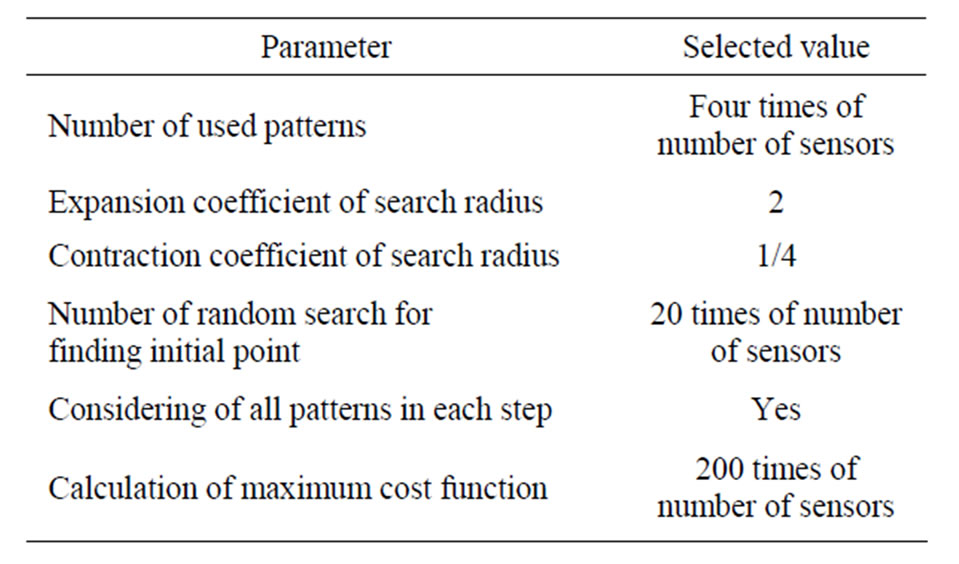
Table 1. Parameters of generalized pattern search method observing no local minimum, the condensation factor acts more rapid than the expansion factor, and thus the method
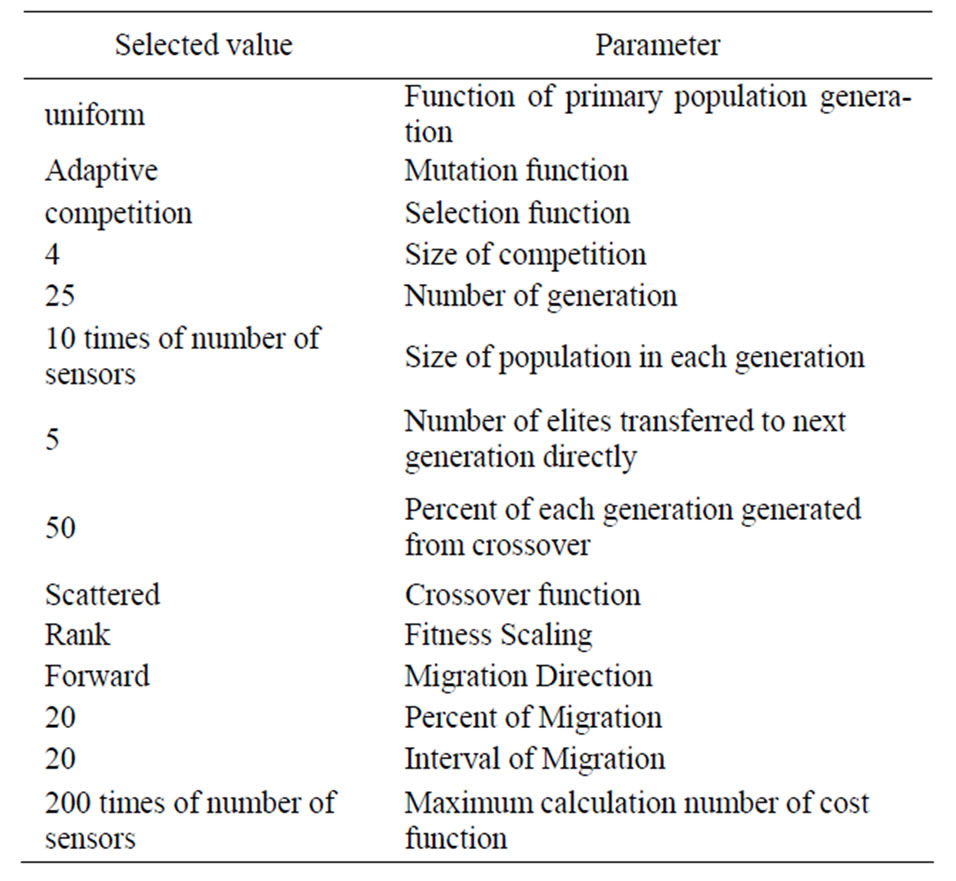
Table 2. Different parameters of genetic algorithm
function is used due to constraint features of the problem in order to prevent problems related to authenticity of mutated offspring in each generation. For constrained optimization problems, it is possible to use uniform or Gaussian distributed mutation but the run time will increase due to infeasibility of some offspring.
6. Comparison Results
The results of these two methods are compared with results of genetic algorithm to evaluate proposed method. From computational complexity view point, proposed method has the same number of function evaluation as genetic algorithm but realization of proposed method sounds simpler than genetic algorithm. To investigate from the view point of positioning quality, the same scenario of Section 3 shown in Figure 1 is used with the difference that in this case 4 sensors are deployed in the lower half-plane. The results of Table 3 and Table 4 are obtained by 100 runs of two methods. It is necessary to note that different scenarios are considered in different simulations in order to compare two methods which have resulted fairly similar results to proposed ones.
In all simulations, the constraint of maximum function evaluation number is assumed 200 times of the number of sensors which leads to reasonable simulation time. In optimizations, cost functions are calculated with a gird of 40 × 40 while final result is calculated and reported with accuracy of 200 × 200 points in the region.
Both methods are evaluated and compared with the criterion of maximum positioning error. Mean and standard deviation and deviation percentage from optimum value are shown in the Table 3 for 100 times of test repetition.

Table 3. Simulation results of proposed method and genetic algorithm for maximum positioning error criterion (optimal value is accessible for maximum error of 766.1)
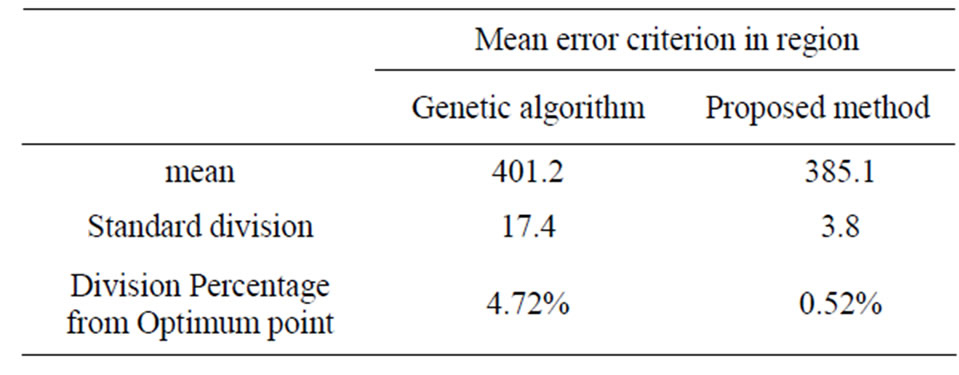
Table 4. Results for mean error on the region for 100 times run of methods which are being compared (optimal value is accessible for mean error of 383.1)
In Table 4 mean of error for 100 times of run are reported for proposed methods in the mentioned region. Optimal value is obtained through minimizing mean of error (rather than maximum of error) on the proposed region but results of methods under comparison are calculated and reported with maximum error criterion.
Table 3 and Table 4 show that the proposed method performs better than genetic algorithm in the region from both view points of maximum and mean of positioning error criterion.
Comparing with the optimal results, maximum error of proposed method which optimization is performed on has 2.5% difference with optimal value while genetic algorithm has error rate of 18.42. Consequently proposed method has better performance from the view point of functionality. Moreover in 100 runs of both methods, standard deviation for results of proposed method is just 7.2; while this value equals 50.3 for genetic algorithm. This shows that the results from genetic algorithm have more variations than those of proposed method.
It can be concluded from Table 4 that if two methods are compared from the view point of mean error in the whole region, it will be concluded that proposed method has 0.84% error respect to optimal value which has a good superiority respect to 4.02% percent for genetic algorithm. Similar to Tabel 3, standard deviation resulted from 100 repetitions of both methods signifies suggested algorithm’s better (less) standard deviation respect to genetic algorithm.
Generally, it can be seen that the proposed method has better results respect to genetic algorithm from the view point of error percentage, stability of results from different runs for two cases of maximum error and mean error.
7. Conclusions
In this paper, a method is proposed based on mutual utilization of random search and generalized pattern search for placement of sensors in positioning applications. This method has higher speed in runtime in addition to less realization complexity and has completely better results respect to genetic algorithm in a way that is very near to optimum. Although this method is investigated for a specific positioning problem, it is possible to generalize it for other positioning applications only with some changes such as in cost function.
REFERENCES
- B. Yang and J. Scheuing, “Cramer-Rao Bound and Optimum Sensor Array for Source Localization from Time Differences of Arrival,” IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Philadelphia, vol. 4, 2005, pp. 961-964.
- B. Yang and J. Scheuing, “A Theoretical Analysis of 2D Sensor Arrays for TDOA Based Localization,” IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Toulouse, Vol. 4, 2006, pp. 961- 964.
- S. M. Kay, “Fundamentals of Statistical Signal Processing: Estimation Theory,” Prentice-Hall, Upper Saddle River, 1993.
- D. J. Torrieri, “Statistical Theory of Passive Location Systems,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 20, No. 2, 1984, pp. 183-198.
- C. Mensing and S. Plass, “Positioning Based on Factor Graph,” EURASIP Journal on Advances in Signal Processing, Vol. 2007, April 2007, pp 1-11.
- C. Mensing, and S. Plass, “Positioning Algorithms for Cellular Networks Using TDOA,” IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Toulouse, Vol. 4, 2006, pp. 513-516.
- R. L. Haupt and S. E. Haupt, “Practical Genetic Algorithms,” 2nd Edition, John Wiley & Sons, Hoboken, 2004.
- S. Olariu, and A. Y. Zomaya, “Handbook of Bioinspired Algorithms and Applications,” Taylor & Francis Group, CRC Press, Boca Raton, 2006.

