Journal of Environmental Protection
Vol. 3 No. 5 (2012) , Article ID: 19518 , 6 pages DOI:10.4236/jep.2012.35052
Support Vector Regression Model of Chlorophyll-a during Spring Algal Bloom in Xiangxi Bay of Three Gorges Reservoir, China
![]()
1College of Chemistry & Life Science, Three Gorges University, Yichang, China; 2College of Hydroelectric & Environment, Three Gorges University, Yichang, China; 3Engineering Research Center of Eco-Environment in Three Gorges Reservoir Region, Ministry of Education, Three Gorges University, Yichang, China.
Email: luohuajun@21cn.com
Received March 4th, 2012; revised April 6th, 2012; accepted May 5th, 2012
Keywords: Support Vector Regression; Chlorophyll-a; Algal Bloom; Three Gorges Reservoir
ABSTRACT
To study the relationship between chlorophyll-a and environmental variables during spring algal bloom in Xiangxi Bay of Three Gorges Reservoir, the support vector regression (SVR) model was established. In surveys, 11 stations have been investigated and 264 samples were collected weekly from March 4 to May 13 in 2007 and February 16 to May 10 in 2008. The parameters in SVR model were optimized by leave one out cross validation. The squared correlation coefficient 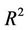 and the cross validated squared correlation coefficient
and the cross validated squared correlation coefficient 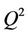 of the optimal SVR model are 0.8202 and 0.7301, respectively. Compared with stepwise multiple linear regression and back propagation artificial neural network models using external validation, the SVR model has been shown to perform well for regression with the predictive squared correlation coefficient
of the optimal SVR model are 0.8202 and 0.7301, respectively. Compared with stepwise multiple linear regression and back propagation artificial neural network models using external validation, the SVR model has been shown to perform well for regression with the predictive squared correlation coefficient 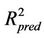 value of 0.7842 for the test set.
value of 0.7842 for the test set.
1. Introduction
The eutrophication of reservoirs and lakes has been a major water quality problem for decades, causing turbid water with high algal biomass [1-3]. This trend is expected to increase by high levels of nutrient input as a result of human activities such as sewage and storm overflows, runoff of commercial fertilizer, and so on [4]. In water research and management, chlorophyll-a is the fundamental index of phytoplankton abundance and a good indicator of algal bloom (a rapid increase in the biomass of phytoplankton) [5-7]. The concentration of chlorophyll-a in aquatic system depends on a number of variables including nutrients, light, temperature, physicochemical properties of the water mass [8] as well as interactions between these physical, chemical and biological compartments of the system. There are many study methods to the relationship between chlorophyll-a and environmental factors such as stepwise multiple linear regression (MLR) analysis [9-12] and artificial neural network (ANN) [13,14]. But the algal bloom is the multivariate interaction and nonlinear process. Many times, linear based methods such as MLR are not able to represent satisfactorily the correlation between chlorophyll-a and respective environmental variables, because these methods do not account for non-linearity. ANN can in principle model nonlinear relations but often difficult to train or even yield unstable models and another drawback is the fact that ANN does not lead to one global or unique solution due to differences in their initial weight set.
Support vector regression (SVR), originally proposed and developed by Vladimir Vapnikn [15,16], is a nonlinear machine learning technique and has many theoretical advantages in the field of chemometrics. These advantages stem from the specific formulation of a (convex) objective function with constraints which is solved using Lagrange Multipliers and has the characteristics that: 1) a global optimal solution exists which will be found, 2) the result is a general solution avoiding overtraining, 3) the solution is sparse and only a limited set of training points contribute to this solution, and 4) nonlinear solutions can be calculated efficiently due to the usage of inner products [17]. So the aim of this present paper is to construct the relationship model between chlorophyll-a and environmental factors during spring algal bloom in Xiangxi Bay of Three Gorges Reservoir using support vector regression method.
2. Materials and Methods
2.1. Area Description
The Three-Gorge Dam (TGD) in China is the world’s largest dam, measuring 2335 m long and 185 m high, and the reservoir created by it has an area of 1080 km2 in 2009 [18]. The Xiangxi River, which lies 38 km upstream from the Dam, is the largest tributary in the Hubei portion of Three-Gorge Reservoir (TGR). This river is 94 km long with a watershed of 3099 km2 (between 110˚25' and 111˚06′E long., 30˚57′ and 31˚34′N lat.) [19]. With impoundment of TGR, the downriver stretch of Xiangxi River was inundated and Xiangxi Bay was formed. Then the water flow velocity has dropped from the original 0.43 - 0.92 m/s [20] to 0.0020 - 0.0041 m/s [21]. So when water temperature increased in spring, there were algal blooms with prolonged retention time and high nutrient concentrations in Xiangxi Bay.
2.2. Sampling and Analysis
Water samples were collected at 11 stations (X0 - X10) in Xiangxi River (Figure 1). Samplings were performed weekly from March 4 to May 13, 2007 and February 16 to May 10, 2008. Water samples were collected at 0.5 m depth from surface in the middle of the river using a 5-L Niskin sampler (Hydrobios-Kiel). Water temperature (WT), dissolved oxygen (DO), pH, turbidity (Turb) were recorded in situ using multi-parameter water quality analyzer (Hydrolab DS5). Total phosphates (TP), phosphate (PO4), total nitrogen (TN), ammonium nitrogen (NH4), nitrate (NO3), silicate (SiO4) were determined in the laboratory using State Environmental Protection Administration (SEPA) standard methods [22]. For chlorophyll-a (Chl-a) analysis, samples filtered through Whatman GF/F filters were extracted with cold 90% acetone and estimated by spectrophotometer [23].
2.3. Support Vector Regression
In support vector regression, the basic idea is to map the data  into a higher dimensional feature space
into a higher dimensional feature space 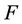 via a nonlinear mapping
via a nonlinear mapping 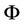 and then to do linear regression in this space [16,17]. Therefore, regression approximation addresses the problem of estimating a function based on a given data set
and then to do linear regression in this space [16,17]. Therefore, regression approximation addresses the problem of estimating a function based on a given data set 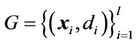 (
(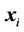 is input vector,
is input vector, 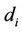 is the desired value). SVR approximates the function in the following form:
is the desired value). SVR approximates the function in the following form:
 (1)
(1)
where 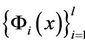 is the set of mappings of input features,
is the set of mappings of input features,
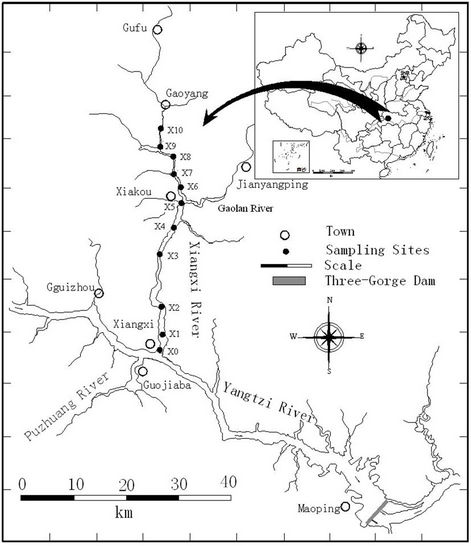
Figure 1. Sampling stations in Xiangxi Bay.
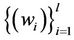 and
and 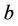 are coefficients. They are estimated by minimizing the regularized risk function
are coefficients. They are estimated by minimizing the regularized risk function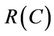 :
:
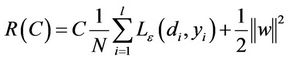 (2)
(2)
where
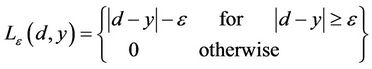 (3)
(3)
and 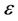 is a prescribed parameter in the insensitive loss function.
is a prescribed parameter in the insensitive loss function.
In Equation (2), 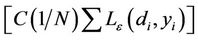 is the socalled empirical error (risk) measured by
is the socalled empirical error (risk) measured by 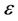 -insensitive loss function
-insensitive loss function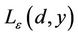 , which indicates that it does not penalize errors below
, which indicates that it does not penalize errors below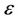 . The second term,
. The second term, 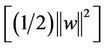 , is used as a measurement of function flatness.
, is used as a measurement of function flatness. 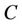 is a regularized constant determining the tradeoff between the training error and the model flatness. Introduction of slack variables
is a regularized constant determining the tradeoff between the training error and the model flatness. Introduction of slack variables 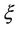 leads Equation (4) to the following constrained function Max:
leads Equation (4) to the following constrained function Max:
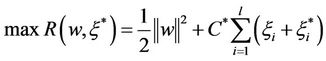 (4)
(4)
s.t.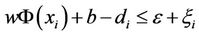 ,
, 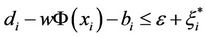 ,
,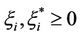 .
.
The minimization of Equation (1) is a standard problem in optimization theory and it can be derived that the weight vector 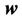 equals the linear combination of the training data:
equals the linear combination of the training data:
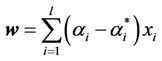
 (5)
(5)
In this formula,  and
and 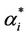 are Lagrange multipliers. Thus, decision function becomes the following form:
are Lagrange multipliers. Thus, decision function becomes the following form:
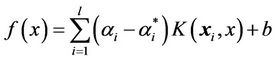 (6)
(6)
where 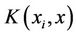 is the kernel function and the value is equal to the inner product of two vectors
is the kernel function and the value is equal to the inner product of two vectors 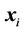 and
and 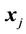 in the feature space
in the feature space . That is,
. That is, 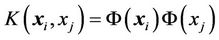 . The most used kernel functions include radial basis function (RBF) kernel, polynomial kernel and linear kernel. For the SVR calculations, a Matlab toolbox was used, developed by Gunn [24].
. The most used kernel functions include radial basis function (RBF) kernel, polynomial kernel and linear kernel. For the SVR calculations, a Matlab toolbox was used, developed by Gunn [24].
3. Results and Discussion
3.1. Selection of the Environmental Factors
Statistic summary of chlorophyll-a and environmental factors during the observation period in Xiangxi Bay of Three Gorges Reservoir are presented in Tables 1 and 2. There is a clear spatial and temporal variation in chlorophyll-a across Xiangxi Bay. The concentration of chlorophyll-a ranged from 0.1280 to 160.2060 mg/m3 in the spring of 2007 and from 1.9380 to 335.7360 mg/m3 in the spring of 2008 with mean values of 11.4910 mg/m3 and 31.8219 mg/m3, respectively. Mean concentration of chlorophyll-a for each station ranged from 3.6723 to 23.7129 mg/m3 in the spring of 2007 and from 17.5191 to 63.6717 mg/m3 in the spring of 2008. The spring algal bloom in 2008 is serious than that in 2007.
The environmental variables were selected using stepwise multiple linear regression method. In the stepwise MLR method, all variables were assessed and evaluated to determine important factors. As the stepping process was terminated, the model with seven important environmental factors was obtained as follows:
 (7)
(7)
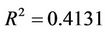 ,
, ,
,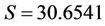 ,
,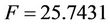 ,
,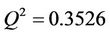 ,
,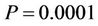 ,
,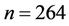
The statistical quality of the regression equation was examined using parameters such as the squared correlation coefficient (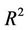 ), the squared adjusted correlation coefficient (
), the squared adjusted correlation coefficient (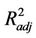 ), the standard error (
), the standard error ( ), the Fisher ratio at the 95% confidence level (
), the Fisher ratio at the 95% confidence level ( ), and the cross validated squared correlation coefficient obtained based on Leave One Out (LOO) method (
), and the cross validated squared correlation coefficient obtained based on Leave One Out (LOO) method (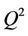 ). The stepwise MLR analysis shows that the environmental variables (DO, pH, Turb, PO4, NH4, NO3, SiO4) are more important to the chlorophyll-a concentration of spring algal bloom in Xiangxi Bay. But Equation (7) only predicted 35.26% of the variance and explained 39.70% of the variance of chlorophyll-a. So the MLR model is not satisfactory.
). The stepwise MLR analysis shows that the environmental variables (DO, pH, Turb, PO4, NH4, NO3, SiO4) are more important to the chlorophyll-a concentration of spring algal bloom in Xiangxi Bay. But Equation (7) only predicted 35.26% of the variance and explained 39.70% of the variance of chlorophyll-a. So the MLR model is not satisfactory.
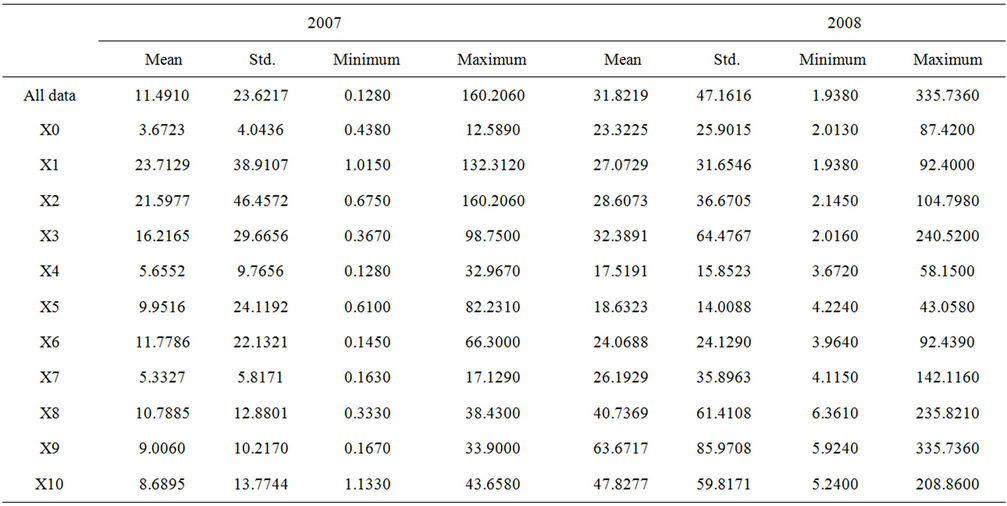
Table 1. Statistic summary of chlorophyll-a (mg/m3) during the observation period in Xiangxi Bay.
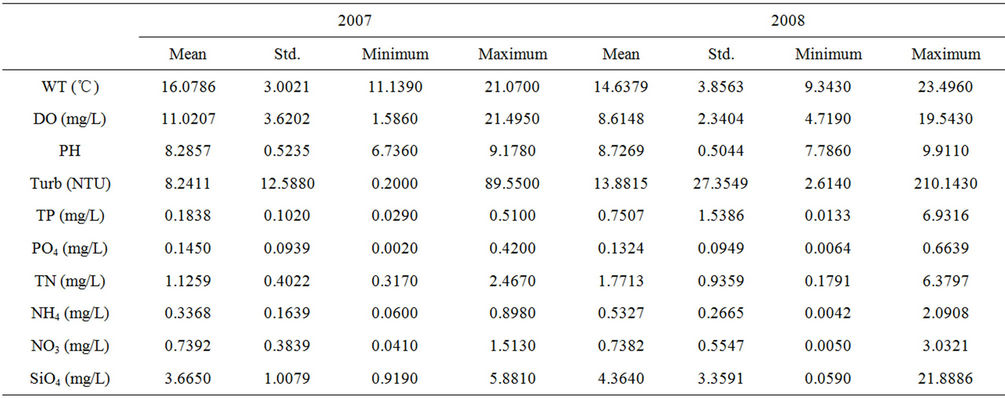
Table 2. Statistic summary of environmental factors during the observation period in Xiangxi Bay.
3.2. Selection of the SVR Model Parameters
The resulting environmental factors in Equation (7) decided by stepwise MLR were used for SVR model. The performance of SVR model is related to variables as well as the combination of parameters used in the model. So some parameters in SVR (the type of kernel function, the regularization parameter 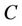 and ε-insensitive loss function) ought to be optimized. In this work,
and ε-insensitive loss function) ought to be optimized. In this work,  was used as a measurement of generalization in leave one out cross validation (LOOCV) of SVR. Figures 2-4 illustrated
was used as a measurement of generalization in leave one out cross validation (LOOCV) of SVR. Figures 2-4 illustrated 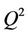 versus
versus 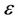 and
and 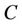 with different kernel functions [RBF with a width of
with different kernel functions [RBF with a width of  = 0.10, polynomial, linear] respectively. It is found that optimal SVR model with
= 0.10, polynomial, linear] respectively. It is found that optimal SVR model with  = 0.7301 is available when the kernel function is polynomial with
= 0.7301 is available when the kernel function is polynomial with  = 0.03 and
= 0.03 and 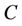 = 150. Figure 5 shows the calculated values of optimal SVR model versus observed values for chlorophyll-a (
= 150. Figure 5 shows the calculated values of optimal SVR model versus observed values for chlorophyll-a (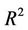 = 0.8202). It can be concluded that the predicted results are in good agreement with the observation ones.
= 0.8202). It can be concluded that the predicted results are in good agreement with the observation ones.
The optimal SVR model was compared with stepwise MLR and back propagation artificial neural network (BPANN). The parameters of BPANN model with three layers used were as follows: the number of hidden nodes was seven; the transformation function was sigmoid; the learning rate and momentum of each epoch were set to 0.30 and 0.20 respectively. External validation was used to compare the predictive capacity of models. The data set was randomly classified into training set (80% data) and test set (20% data) and the predictive 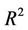 (
( ) values were calculated according to the following equation:
) values were calculated according to the following equation:
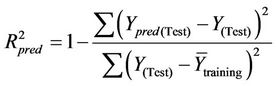 (8)
(8)

Figure 2. 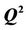 versus
versus  and C with RBF kernel function (σ = 0.10).
and C with RBF kernel function (σ = 0.10).
Figure 3.  versus
versus  and C with polynomial kernel function.
and C with polynomial kernel function.
Figure 4. 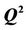 versus
versus 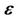 and C with linear kernel function.
and C with linear kernel function.

Figure 5. Observed values versus calculated values for chlorophyll-a using optimal SVR model.
where  and
and 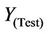 represent the predicted and observed chlorophyll-a values of the test set, respectively.
represent the predicted and observed chlorophyll-a values of the test set, respectively.  is the mean chlorophyll-a value of the training set.
is the mean chlorophyll-a value of the training set.
The 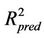 values of MLR, BPANN and SVR models were 0.4127, 0.7644 and 0.7842 respectively. Figure 6 shows the predicted values of optimal SVR model versus observed values for chlorophyll-a. Based on the above results. The SVR method has been shown to perform well for regression and be a useful and powerful technique to construct the chlorophyll-a model during spring algal bloom.
values of MLR, BPANN and SVR models were 0.4127, 0.7644 and 0.7842 respectively. Figure 6 shows the predicted values of optimal SVR model versus observed values for chlorophyll-a. Based on the above results. The SVR method has been shown to perform well for regression and be a useful and powerful technique to construct the chlorophyll-a model during spring algal bloom.
4. Conclusion
The support vector regression model of chlorophyll-a during spring algal bloom in Xiangxi Bay of Three

Figure 6. Observed values versus predicted values for chlorophyll-a using optimal SVR model.
Gorges Reservoir was established. Using stepwise MLR method, the important environmental variables (DO, pH, Turb, PO4, NH4, NO3 and SiO4) were selected. The parameters in SVR such as the type of kernel function, the regularization parameter 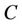 and
and 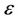 -insensitive loss function were optimized by leave one out cross validation.
-insensitive loss function were optimized by leave one out cross validation.  and
and 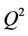 of the optimal SVR model are 0.8202 and 0.7301, respectively. Compared with MLR and BPANN models, the SVR model has been shown to perform well for regression with the
of the optimal SVR model are 0.8202 and 0.7301, respectively. Compared with MLR and BPANN models, the SVR model has been shown to perform well for regression with the  value of 0.7842 for the test set.
value of 0.7842 for the test set.
5. Acknowledgements
This work was funded by National Natural Science Foundation of China (No. 50679038, 51009080), National Science and Technology Support Program of China (No. 2008BAB29B09), National Water Special Project of China (2008ZX07104-004) and Hubei Province Ministry of Environmental Protection, China (No. 2008HB08). We thank Daobin Ji, Zhengjian Yang, Zhongqiang Yi, Jun Ma, Yanmei Su, Xia Yang and Qiaoli Cao for their assistance in the field and lab.
REFERENCES
- S. R. Carpenter, D. Ludwig and W. A. Brock, “Management of Eutrophication for Lakes Subject to Potentially Irreversible Change,” Ecological Applications, Vol. 9, 1999, pp. 751-771. doi:10.1890/1051-0761(1999)009[0751:MOEFLS]2.0.CO;2
- D. W. Schindler, “Recent Advances in the Understanding and Management of Eutrophication,” Limnology and Oceanography, Vol. 51, 2006, pp. 356-363. doi:10.4319/lo.2006.51.1_part_2.0356
- I. Kagalou, E. Papastergiadou and I. Leonardos, “Long Term Changes in the Eutrophication Process in a Shallow Mediterranean Lake Ecosystem of W. Greece: Response after the Reduction of External Load,” Journal of Environmental Management, Vol. 87, No. 3, 2008, pp. 497- 506. doi:10.1016/j.jenvman.2007.01.039
- H. B. Glasgow Jr. and J. M. Burkholder, “Water Quality Trends and Management Implications from a Five-Year Study of a Eutrophic Estuary,” Ecological Applications, Vol. 10, 2000, pp. 1024-1046. doi:10.1890/1051-0761(2000)010[1024:WQTAMI]2.0.CO;2
- P. J. Dillon and F. H. Rigler, “The Phosphorus-Chlorophyll Relationship in Lakes,” Limnology and Oceanography, Vol. 19, No. 5, 1974, pp. 767-773. doi:10.4319/lo.1974.19.5.0767
- K. An and S. S. Park, “Indirect Influence of the Summer Monsoon on Chlorophyll-Total Phosphorus Models in Reservoirs: A Case Study,” Ecological Modelling, Vol. 152, No. 2-3, 2002, pp. 191-203. doi:10.1016/S0304-3800(02)00020-0
- G. Phillips, O. P. Pietilainen, L. Carvalho, A. Solimini, A. L. Solheim and A. Cardoso, “Chlorophyll-Nutrient Relationships of Different Lake Types Using a Large European Dataset,” Aquatic Ecology, Vol. 42, No. 2, 2008, pp. 213-226. doi:10.1007/s10452-008-9180-0
- L. Hakanson, J. M. Malmaeus, U. Bodemer and V. Gerhardt, “Coefficients of Variation for Chlorophyll, Green Algae, Diatoms, Cryptophytes And Blue-Greens in Rivers as a Basis For Predictive Modelling and Aquatic Management,” Ecological Modelling, Vol. 169, No. 1, 2003, pp. 179-196. doi:10.1016/S0304-3800(03)00269-2
- K. K. Balachandran, K. V. Jayalakshmy, C. M. Laluraj, M. Nair, T. Joseph and P. Sheeba, “Step-Up Multiple Regression Model to Compute Chlorophyll a in the Coastal Waters off Cochin, Southwest Coast of India,” Environmental Monitoring and Assessment, Vol. 139, No. 1-3, 2008, pp. 217-226. doi:10.1007/s10661-007-9829-5
- N. K. Sharma, D. Mohan and A. K. Rai, “Predicting Phytoplankton Growth and Dynamics in Relation to Physico-Chemical Characteristics of Water Body,” Water Air & Soil Pollution, Vol. 202, No. 1-4, 2009, pp. 325-333. doi:10.1007/s11270-009-9979-x
- K. H. Cho, J.-H. Kang, S. J. Ki, Y. Park, S. M. Cha and J. H. Kim, “Determination of the Optimal Parameters in Regression Models for the Prediction of Chlorophyll-a: A Case Study of the Yeongsan Reservoir, Korea,” Science of the Total Environment, Vol. 407, No. 8, 2009, pp. 2536- 2545. doi:10.1016/j.scitotenv.2009.01.017
- Y. Liu, H. Guo and P. Yang, “Exploring the Influence of Lake Water Chemistry on Chlorophyll-a: A Multivariate Statistical Model Analysis,” Ecological Modelling, Vol. 221, No. 4, 2010, pp. 681-688. doi:10.1016/j.ecolmodel.2009.03.010
- M. Xu, G. M. Zeng, X. Y. Xu and G. H. Huang, “Application of Bayesian Regularized BP Neural Network Model for Analysis of Aquatic Ecological Data—A Case Study of Chlorophyll a Prediction in Nanzui Water Area of Dongting Lake,” Journal of Environmental Science, Vol. 17, No. 6, 2005, pp. 946-952.
- K.-S. Jeong, D.-K. Kim and G.-J. Joo, “River Phytoplankton Prediction Model by Artificial Neural Network: Model Performance and Selection of Input Variables to Predict Time-Series Phytoplankton Proliferations in a Regulated River System,” Ecological Informatics, Vol. 1, No. 3, 2006, pp. 235-245. doi:10.1016/j.ecoinf.2006.04.001
- V. Vapnik, “Statistical Learning Theory,” Wiley, New York, 1998.
- V. Vapnik, “An Overview of Statistical Learning Theory,” IEEE Transactions on Neural Networks, Vol. 10, No. 5, 1999, pp. 988-999. doi:10.1109/72.788640
- U. Thissen, R. van Brakel, A. P. de Weijer, W. J. Melssen and L. M. C. Buydens, “Using Support Vector Machines for Time Series Prediction,” Chemometrics and Intelligent Laboratory Systems, Vol. 69, No. 1-2, 2003, pp. 35- 49. doi:10.1016/S0169-7439(03)00111-4
- J. G. Wu, J. H. Huang, X. G. Han, Z. Q. Xie and X. M. Gao, “Three-Gorge Dam—Experiment in Habitat Fragmentation?” Science, Vol. 300, No. 5623, 2003, pp. 1239- 1240. doi:10.1126/science.1083312
- L. Ye, D. F. Li, T. Tang, X. D. Qu and Q. H. Cai, “Spatial Distribution of Water Quality in Xiangxi River, China,” China Journal of Applied Ecology, Vol. 14, No. 11, 2003, pp. 1959-1962.
- T. Tang, D. F. Li, W. B. Pan, X. D. Qu and Q. H. Cai, “River Continuum Characteristics of Xiangxi River,” China Journal of Applied Ecology, Vol. 15, No. 1, 2004, pp. 141-144.
- H. Y. Wang, “Effects of the Three Gorges Reservoir on the Water Environment of the Xiangxi River with the Proposal of Countermeasures,” Resource and Environment of Yangtze Basin, Vol. 14, No. 2, 2005, pp. 233-237.
- X. C. Jin and Q. Y. Tu, “Criterion of Eutrophication Survey on Lakes,” 2nd Edition, Environmental Science Press, Beijing, 1990.
- A. J. Lewitus, E. T. Koepfler and J. T. Morris, “Seasonal Variation in the Regulation of Phytoplankton by Nitrogen and Grazing in a Salt Marsh Estuary,” Limnology and Oceanography, Vol. 43, No. 4, 1998, pp. 636-646. doi:10.4319/lo.1998.43.4.0636
- S. R. Gunn, “Support Vector Machines for Classification and Regression,” Technical Report, Image Speech and Intelligent Systems Research Group, University of Southampton, Southampton, 1997. http://www.isis.ecs.soton.ac.uk/isystems/kernel/

