Smart Grid and Renewable Energy
Vol.2 No.2(2011), Article ID:4959,10 pages DOI:10.4236/sgre.2011.22014
Investigation on the Excitation Capacitor for a Wind Pumping Plant Using Induction Generator
![]()
University of Sfax, Unité de Commande de Machines et Réseaux de Puissance CMERP-ENIS, Sfax, Tunisia.
Email: manel_zouhir_ouali@yahoo.fr; maherchaabane@gmail.com; mba.kamoun@enis.rnu.tn
Received February 27th, 2011; revised March 28th, 2011; accepted April 2nd, 2011.
Keywords: SEIG, IM, Centrifugal Pump, Optimal Excitation Capacitor, Wind Rotor Speed
ABSTRACT
This paper presents a SEIG-IM system using a self excited induction generator driven by wind turbine and supplying an induction motor which is coupled to a centrifugal pump. A method to describe the steady state performance based on nodal analysis is presented. Furthermore, a dynamic analysis and performance characteristics are examined. The proposed methodology is discussed in order to optimize the quantity of the pumped water. Therefore an optimal excitation capacitor for a given wind rotor speed is determined and a suitable operation mode of the system is established.
1. Introduction
Owing the increase of the depletion of conventional energy and the degradation of environmental conditions, the development of suitable isolated power generators driven by renewable energies as solar, geothermal, biomass, hydro and wind energy resources are envisaged to replace conventional resources [1]. Wind energy is considered the most adopted, attractive and practical of all renewable energies as it is available in most sites. It consists of the conversion of kinetic energy into a useful form of energy such as mechanical or electrical [2]. The main application is the wind water pumping using turbines [3]. Many types of generator are used for stand alone power generation in remote and windy areas such as permanent magnet, brushless, synchronous, asynchronous, variable reluctance. Self Excited Induction Generator (SEIG) is the most used for low and medium power generation thanks to its lower cost, easy operation, brushless construction and easy maintenance. It can sustain self excitation and supply electric power while an appropriate value of a capacitor banc is properly connected across its stator terminals [4,5].
SEIG driven by regulated or unregulated turbine and supplying a static or dynamic load has been undertaken by many researchers and is well discussed in literature [6,7]. Investigation in steady state operation are essentially based on the analysis of the per phase equivalent circuit of the three phase induction machine and on either the loop impedance [8] or the nodal admittance concept [9].
As for the dynamic and transient operation, it was treated for no load and for different loads: resistive [10], inductive [11], capacitive [12], induction motor [13], DC load, etc. In this context, this work presents an investigation on a wind pumping plant (SEIG-IM) using a SEIG driven by wind turbine and supplying an Induction Motor (IM) which is coupled to a centrifugal pump. A SEIG-IM performance analysis is developed so as to determine the optimal excitation capacitor which offers maximum pumped water for a given wind rotor speed.
This paper is organized as follows: section two gives the system modeling in static and a dynamic state. Section three shows the computation procedure which provides the optimal excitation capacitor that maximizes the volume of the pumped water. Simulation results are discussed in section four. Finally a conclusion resumes the developed work and its features.
2. System Modeling
2.1. System Configuration
The pumping unit, shown by Figure 1, is composed of a wind turbine which converts wind kinetic energy into electricity by means of SEIG. The produced power is used to supply an induction motor coupled to a centrifugal water pump. As the SEIG requires reactive power for
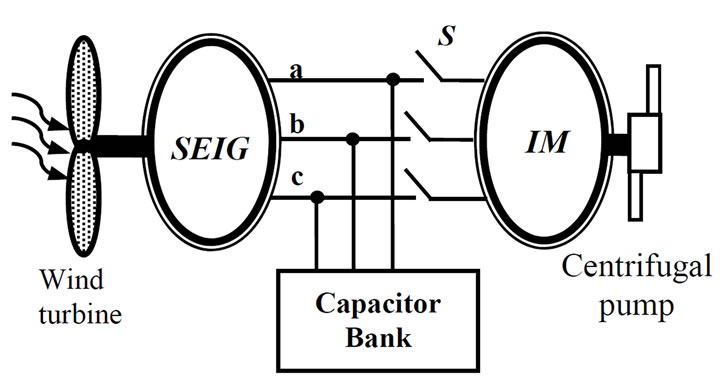
Figure 1. Wind electric pumping system.
its excitation, a three phase capacitor bank is connected across its stator terminals.
The IM cannot be supplied unless the SEIG stator voltage build up process occurs. For this reason an operating mode switcher selects first the no load condition ( ) until the voltage build up process is accomplished. Subsequently the switcher is turned on (
) until the voltage build up process is accomplished. Subsequently the switcher is turned on (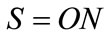 ) so as to connect the IM to the SEIG.
) so as to connect the IM to the SEIG.
In order to analyze the performances of self excited induction generator witch supplies an induction motor driving water pump, a system modeling is required. Following, a steady state and dynamic modeling are presented.
2.2. Steady State Modeling
For a given excitation capacitance and wind rotor speed, the steady state of SEIG-IM can be studied unless the stator angular frequency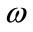 , the IM angular velocity
, the IM angular velocity 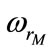 and the magnetizing inductance of the induction generator
and the magnetizing inductance of the induction generator 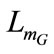 are known. By examining per phase equivalent circuit (Figure 2) and considering the magnetization characteristics of both induction machines, two equations are determined. A third equation is deduced from the system power balance. All circuit’s parameters except the magnetizing inductances
are known. By examining per phase equivalent circuit (Figure 2) and considering the magnetization characteristics of both induction machines, two equations are determined. A third equation is deduced from the system power balance. All circuit’s parameters except the magnetizing inductances 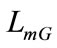 and
and 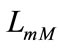 are assumed to be constant and insensitive to saturation. In addition, core losses and effect harmonics in the machine have been ignored.
are assumed to be constant and insensitive to saturation. In addition, core losses and effect harmonics in the machine have been ignored.
The loop equation involving the stator voltage Vs is written as:
 (1)
(1)
where, Y is the total loop admittance giving by:
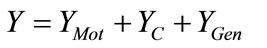 (2)
(2)
The expression of admittance capacitive 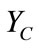 is giving by:
is giving by:
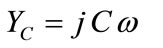 (3)
(3)
The induction generator admittance 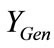 is expressed as:
is expressed as:
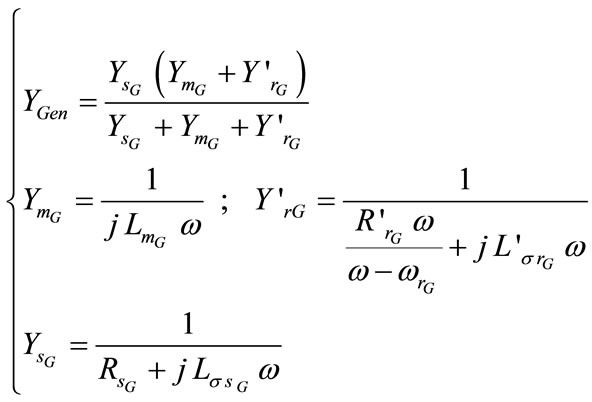 (4)
(4)
As a consequence of the symmetry of per phase equivalent circuit, the expression of induction motor admittance 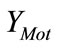 can be deduced from that of
can be deduced from that of 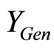 by replacing the index
by replacing the index  by
by 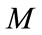 and
and 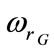 by
by .
.
Since under steady – state excitation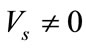 , it implies that
, it implies that  or both real and imaginary parts of
or both real and imaginary parts of 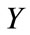 are equal to zeros:
are equal to zeros:
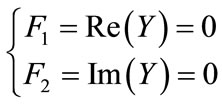 (5)
(5)
While the rotational loss torque, the windage losses and damping factor are ignored, the mechanical power of induction motor 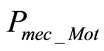 is equal to that of centrifugal pump
is equal to that of centrifugal pump , and it can be expressed as a function of
, and it can be expressed as a function of
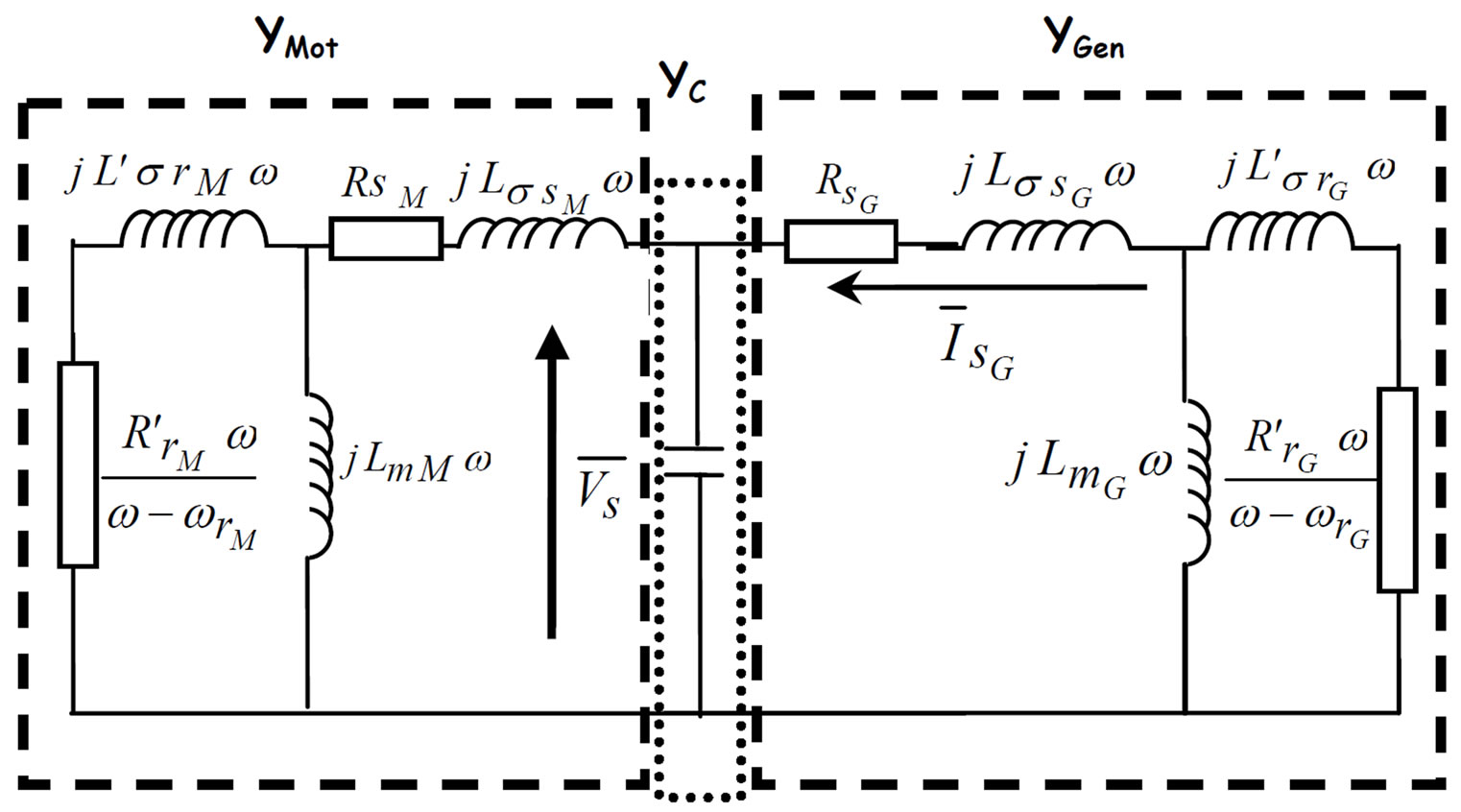
Figure 2. Per phase equivalent circuit of self excited induction generator feeding an induction pump motor.
the equivalent circuit parameters:
 (6)
(6)
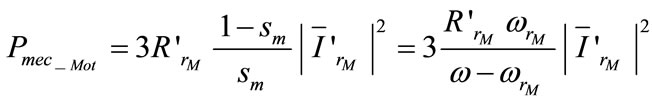 (7)
(7)
The mechanical power of the centrifugal pump is giving by [14]:
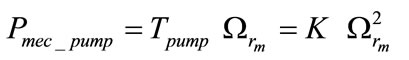 (8)
(8)
where the Tpump is the load torque of the pump and 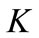 is a coefficient computed by:
is a coefficient computed by:
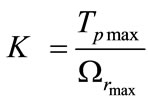 (9)
(9)
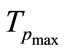 is the maximum rated torque and
is the maximum rated torque and  is the maximum rated mechanical motor speed.
is the maximum rated mechanical motor speed.
The IM rotor current expression can by obtained by the application of voltage divider theorem to the motor circuit model:
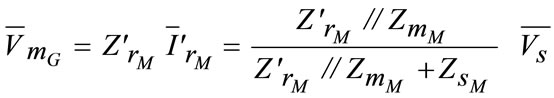 (10)
(10)
The stator voltage can also be expressed by the application of voltage divider theorem to the generator circuit model:
 (11)
(11)
where
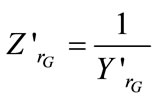 ,
, 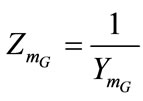 ,
, 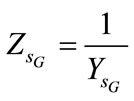 ,
,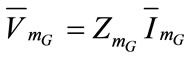 .
.
The motor impedances expressions  are calculated by the same way as above by replacing the index
are calculated by the same way as above by replacing the index  by
by 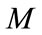 and
and by
by 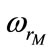 in expressions of
in expressions of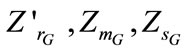 .
.
 (12)
(12)
The IM magnetizing current  is formulated as a function of
is formulated as a function of :
:
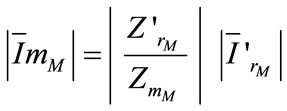 (13)
(13)
Equations (5) and (6) are nonlinear, where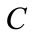 ,
, 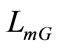 ,
,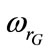 ,
,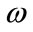 and
and  are unknown variables. Therefore, in order to solve these equations, two of these variables must be specified. Two approaches are considered in literature [8,9,15]:
are unknown variables. Therefore, in order to solve these equations, two of these variables must be specified. Two approaches are considered in literature [8,9,15]:
• To determine the steady state performance of the SEIG-IM system, 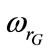 and
and 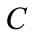 must be specified and the equations must be solved for
must be specified and the equations must be solved for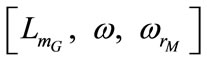 .
.
• To determine the minimum capacitor value required for the onset of self-excitation process ,
, 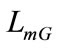 and
and  must be specified and the equations must be solved for
must be specified and the equations must be solved for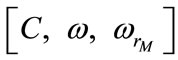 .
.
The above mentioned equations can be solved by adopting the method of Newton Raphson and calculating the corresponding Jacobian matrix.
Since saturation phenomenon is a significant factor in the processes of self excited induction generator, the variation of magnetic generator inductance  should be taken into consideration to find the correct voltage build up. Therefore, at each sampling step, the value of the magnetic generator current
should be taken into consideration to find the correct voltage build up. Therefore, at each sampling step, the value of the magnetic generator current  is adjusted according to
is adjusted according to 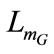 thanks to a spline interpolation of the generator magnetization measured characteristic. Then,
thanks to a spline interpolation of the generator magnetization measured characteristic. Then, 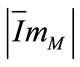 is computed using Equations 12 and 13. Finally,
is computed using Equations 12 and 13. Finally,  is adjusted according to the
is adjusted according to the  value thanks to a spline interpolation of the motor magnetizing measured characteristic.
value thanks to a spline interpolation of the motor magnetizing measured characteristic.
2.3. Dynamic State Modeling
In order to analyze the transient response of SEIG-IM, a dynamic system modeling of the SEIG, the IM and the centrifugal pump is necessary.
2.3.1. Induction Machines Models
Using the generator convention, the voltage equations of the SEIG are expressed as:
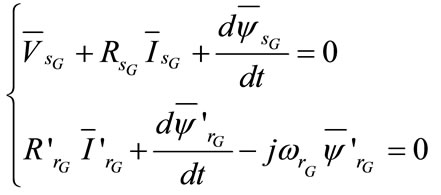 (14)
(14)
where, the fluxes of the SEIG are giving by:
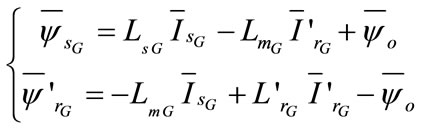 (15)
(15)
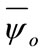 represents the initial residual flux. The generator magnetizing flux is computed by:
represents the initial residual flux. The generator magnetizing flux is computed by:
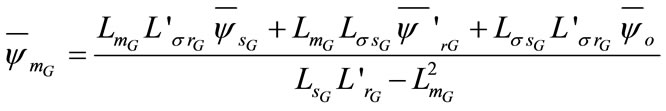 (16)
(16)
In the same way and by adopting the motor convention, the voltage equations and fluxes of IM are respectively given by:
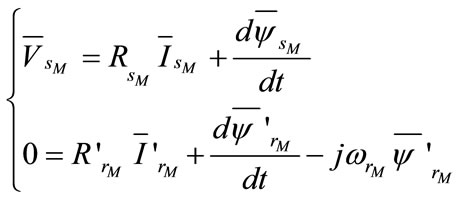 (17)
(17)
 (18)
(18)
The motor magnetizing flux is computed by:
 (19)
(19)
The stator voltage of both machines is expressed as:
 (20)
(20)
 represents the capacity current. It is given by:
represents the capacity current. It is given by:
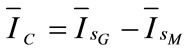 (21)
(21)
To take account of the non linearity of the magnetic material, the magnetization curve of both machines SEIG and IM are implemented in their models: at each sampling step, the value of 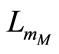 and
and  are adjusted. The mechanical equation that describes this system is:
are adjusted. The mechanical equation that describes this system is:
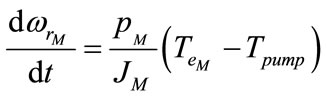 (22)
(22)
where, 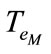 and
and 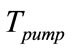 represent respectively the electromagnetic torque produced by IM and the load torque of the pump.
represent respectively the electromagnetic torque produced by IM and the load torque of the pump.
2.3.2. Centrifugal Pump Model
Due to mechanical losses, the useful power of centrifugal pump coupled to the shaft of IM is:
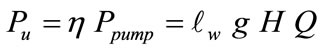 (23)
(23)
where 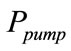 is the mechanical power given by Equation (8),
is the mechanical power given by Equation (8), 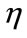 represents the pump efficiency,
represents the pump efficiency, 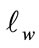 is the water density (
is the water density (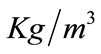 ),
), is the gravity acceleration (
is the gravity acceleration (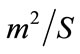 ),
),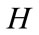 is the height of rise (
is the height of rise ( ) and
) and 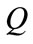 is the flow (
is the flow (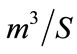 ). For a pumping period
). For a pumping period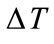 , the volume of pumped water (
, the volume of pumped water (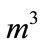 ) is computed by:
) is computed by:
 (24)
(24)
3. Determination of the Optimal Capacitor
The work aims to maximize the amount of the pumped water by minimizing the excitation capacitance value. Referring to Equations 8, 23 and 24, the volume of the pumped water increases while raising the IM mechanical power (rotor speed). This is ensured by minimizing the excitation capacitance value. Therefore, the criterion defined by “minimize 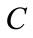 so that
so that 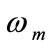 is maximum” must be checked using an iterative procedure. First, it is necessary to determine the minimum excitation capacitance value for which the SEIG stator voltage builds upoccurs at IM load operation
is maximum” must be checked using an iterative procedure. First, it is necessary to determine the minimum excitation capacitance value for which the SEIG stator voltage builds upoccurs at IM load operation . Then the maximum excitation capacitance
. Then the maximum excitation capacitance 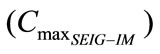 is calculated considering the limitation of the current stator at 120% of its nominal value to avoid destructive over current which causes serious damage to the system equipments. Finally, the following steps are to proceed:
is calculated considering the limitation of the current stator at 120% of its nominal value to avoid destructive over current which causes serious damage to the system equipments. Finally, the following steps are to proceed:
1) For a given wind rotor speed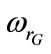 , the excitation capacitance is assumed equal to
, the excitation capacitance is assumed equal to  for which the parameters of the centrifugal pump, the parameters of the two machines and their magnetization characteristics are defined.
for which the parameters of the centrifugal pump, the parameters of the two machines and their magnetization characteristics are defined.
2) The Newton Raphson iterative method is used as follows:
a) The initial conditions are fixed and the substitutions of parameters adopted in the resolution of Equations 1-13 are calculated.
b) The vector, the corresponding Jacobian matrix and the
vector, the corresponding Jacobian matrix and the 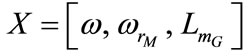 vector are determined.
vector are determined.
c) The 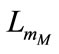 value is estimated using
value is estimated using  value, magnetic characteristics of both machines and Equations 12-13.
value, magnetic characteristics of both machines and Equations 12-13.
d) Using the new obtained values, repeat steps a, b and c until the error on the vector  is less than a given precision. In this case, the convergence is considered reached.
is less than a given precision. In this case, the convergence is considered reached.
3) The obtained value of 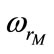 is saved and then the excitation capacitance is incremented by
is saved and then the excitation capacitance is incremented by .
.
4) Repeat steps 2 and 3 until 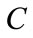 value is equal or greater then
value is equal or greater then .
.
Thus, for each value of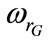 , a database is established in order to study the IM wind rotor variation function of the excitation capacitance. The minimum value of
, a database is established in order to study the IM wind rotor variation function of the excitation capacitance. The minimum value of 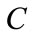 for which
for which 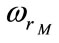 becomes maximum and substantially constant is chosen. This value is considered as the optimal capacitor.
becomes maximum and substantially constant is chosen. This value is considered as the optimal capacitor.
4. Results and Discussions
The proposed method of evaluating the steady and dynamic state characteristic of a SEIG-IM is tested referring to a three-phase induction generator: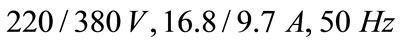
 .
.
This later supplies an induction motor:
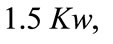 .
.
The fixed parameters of both induction machines used in simulation are:

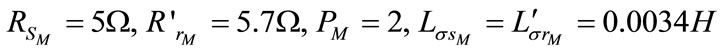
The magnetizing inductances of the both induction machines are measured as a function of the magnetizing currents by performing an open circuit test for which the machines are driven at synchronous speed and a variable voltage source is applied to the stator (Figure 3).
4.1. Steady State Results
The behaviours of the stator voltage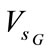 , the IG stator current
, the IG stator current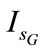 , the IM stator current
, the IM stator current 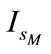 and the frequency are plotted as a function of the excitation capacitance and the wind rotor speed. The curves network for
and the frequency are plotted as a function of the excitation capacitance and the wind rotor speed. The curves network for 
 and different values of
and different values of  (a step of 0.025 is considered) are shown by Figures 4 and 5. It is noticed that the increase in
(a step of 0.025 is considered) are shown by Figures 4 and 5. It is noticed that the increase in 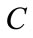 causes a gradually increase of
causes a gradually increase of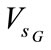 ,
, 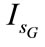 and
and . As for the frequency
. As for the frequency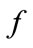 it increases then remains constant.
it increases then remains constant.
A similar curves set of 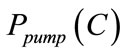 for different values of
for different values of  is shown by Figure 6. For each curve, it is clear that by increasing
is shown by Figure 6. For each curve, it is clear that by increasing 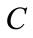 from
from  to
to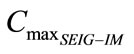 ,
, 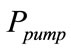 increases gradually. Nevertheless, since a certain value of
increases gradually. Nevertheless, since a certain value of ,
, 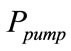 becomes maximum and substantially constant. At this functional point, the obtained value of
becomes maximum and substantially constant. At this functional point, the obtained value of  is considered as optimal
is considered as optimal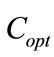 .
.
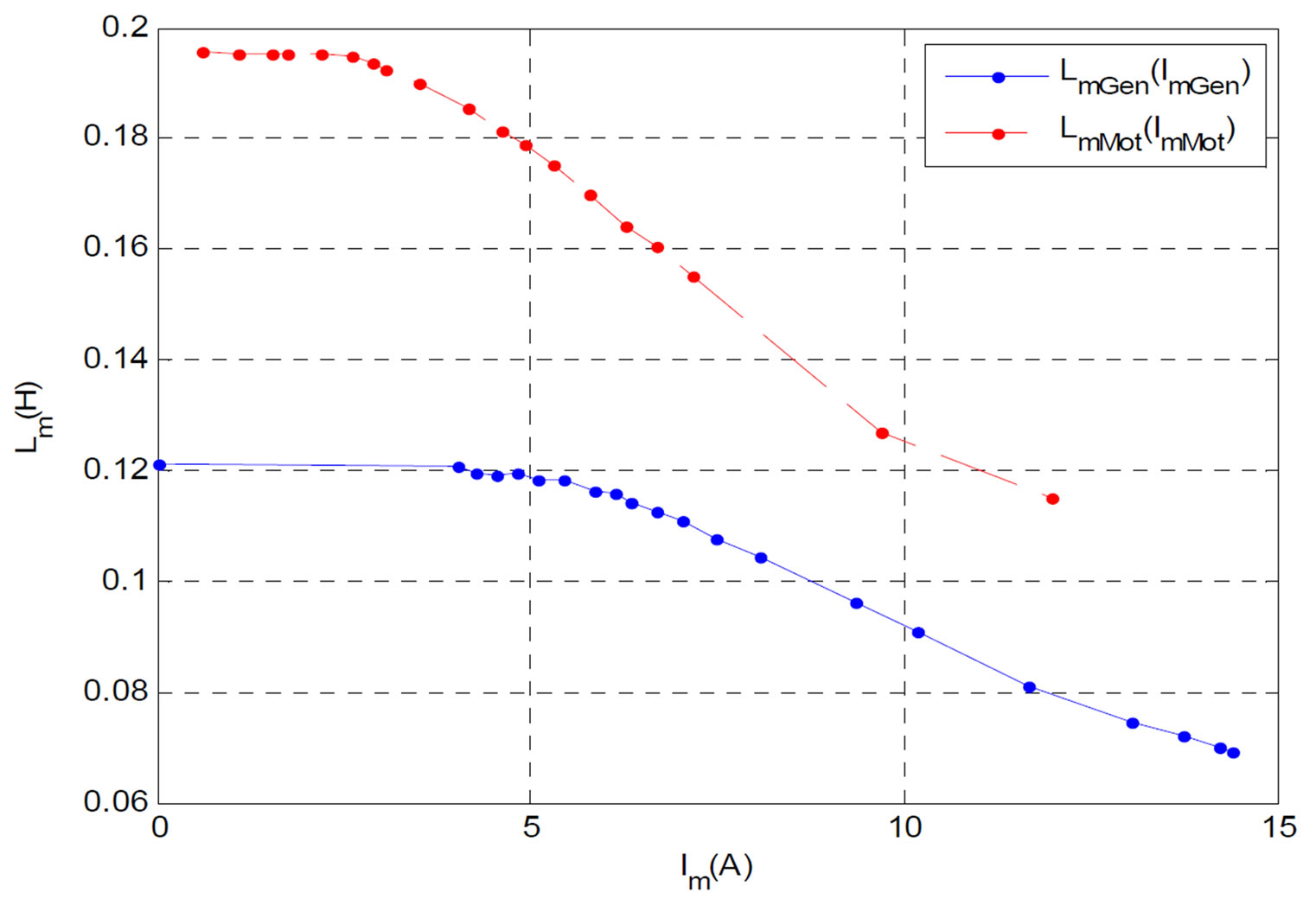
Figure 3. Magnetization characteristics of both induction.
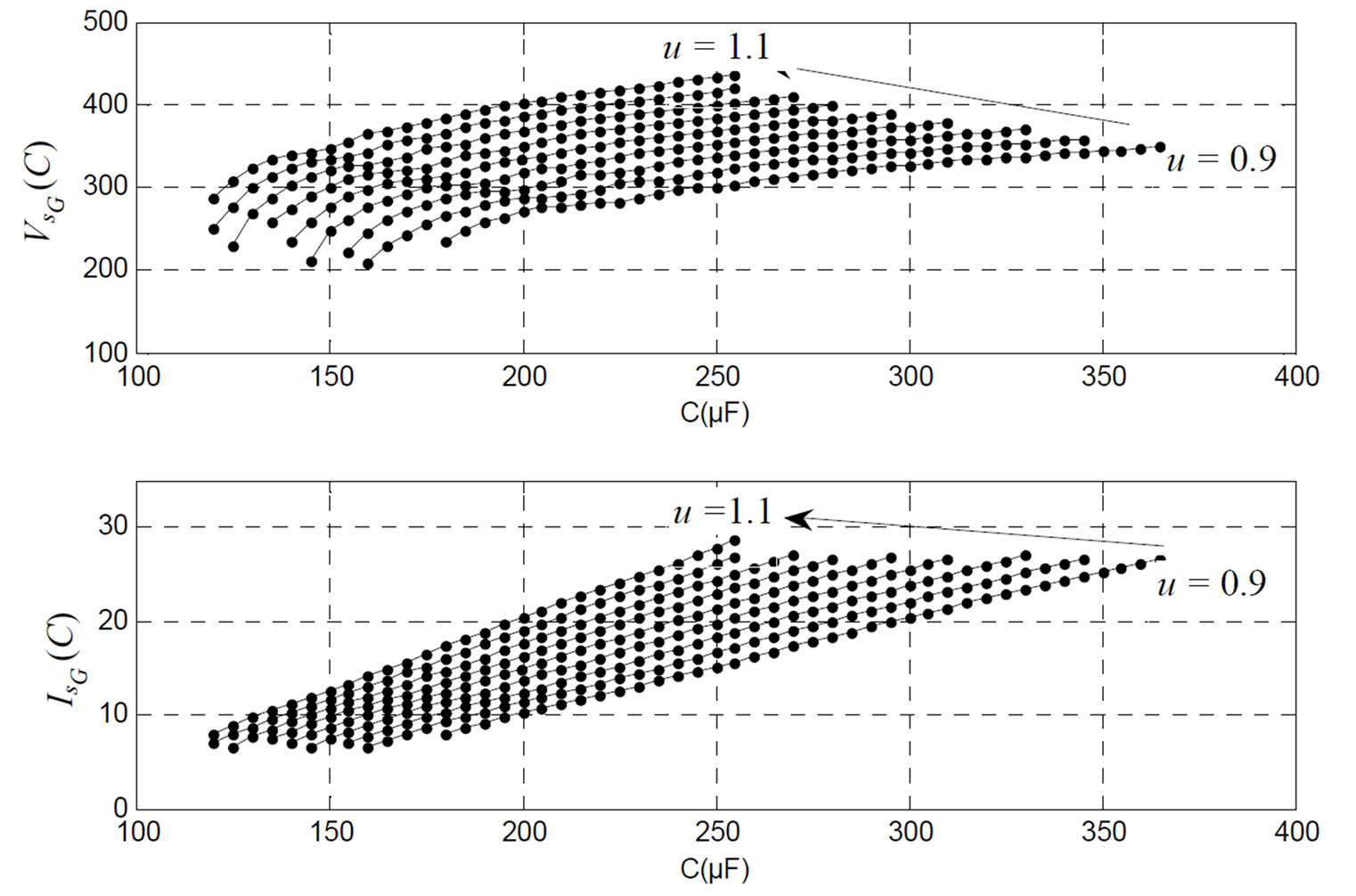
Figure 4.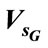 ,
, 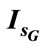 variation function of excitation capacitance for various values of
variation function of excitation capacitance for various values of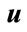 .
.

Figure 5 .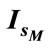 ,
, 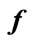 variation function of excitation capacitance for various values of
variation function of excitation capacitance for various values of .
.
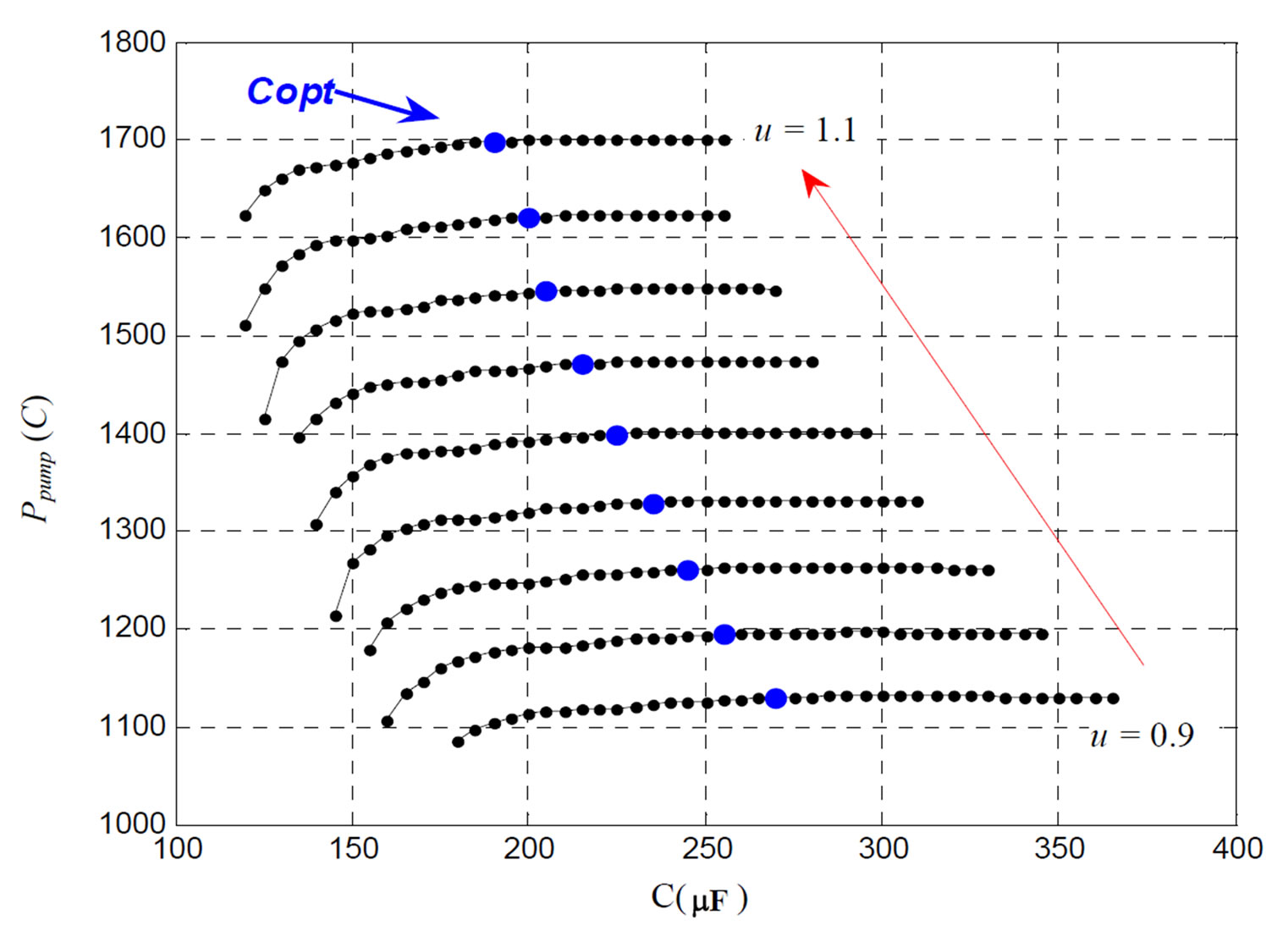
Figure 6. 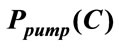 characteristics for various.
characteristics for various.
4.2. Dynamic Results
In order to determine the suitable operation mode of SEIG-IM system driven by wind turbine at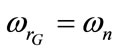 , the effect of the capacitance value on the stator voltage waveform is studied. Firstly, C is equal to
, the effect of the capacitance value on the stator voltage waveform is studied. Firstly, C is equal to . It is shown that the self excitation process does not occur (Figure 7). This proves the necessity of functioning in two stages. The induction generator is self excited at no load (
. It is shown that the self excitation process does not occur (Figure 7). This proves the necessity of functioning in two stages. The induction generator is self excited at no load ( in first stage),
in first stage), 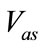 is established and reaches its steady state value; then the motor pump starts operation after a delay of about
is established and reaches its steady state value; then the motor pump starts operation after a delay of about  (
(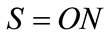 in second stage).
in second stage).
Secondly, when  is equal to
is equal to  during the two stages, the stator voltage is established in first stage and decreases rapidly to be eliminated during the second stage (at IM operation) (Figure 8).
during the two stages, the stator voltage is established in first stage and decreases rapidly to be eliminated during the second stage (at IM operation) (Figure 8).
Subsequently,  is equal to
is equal to  during the two stages (Figures 9(a) and 9(b)).
during the two stages (Figures 9(a) and 9(b)).
The self excitation process is well established and maintained but 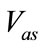 and
and 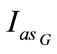 can reach peaks at no load operation. This phenomenon is especially important when working at high wind rotor speed
can reach peaks at no load operation. This phenomenon is especially important when working at high wind rotor speed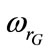 .
.
Hence, the value of 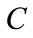 is fixed at
is fixed at  during the first stage and respectively at
during the first stage and respectively at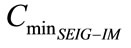 ,
,  and
and 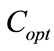 during the second stage (Figures 10
during the second stage (Figures 10

Figure 7.  Variation with time at
Variation with time at 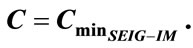

Figure 8. 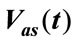 characteristic at
characteristic at 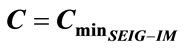 during the two stages of operation.
during the two stages of operation.
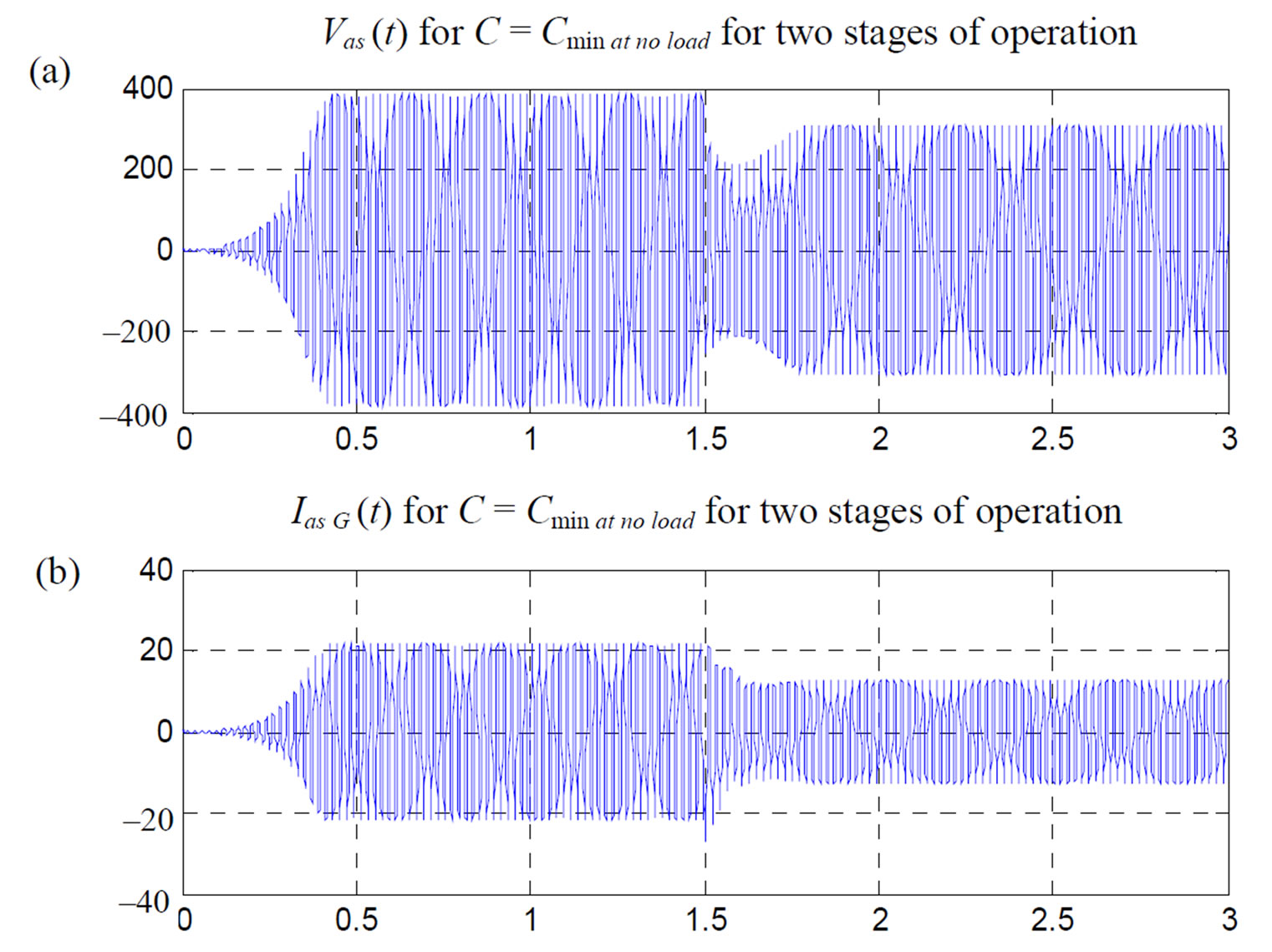
Figure 9.  and
and  characteristics at
characteristics at  during the two stages.
during the two stages.
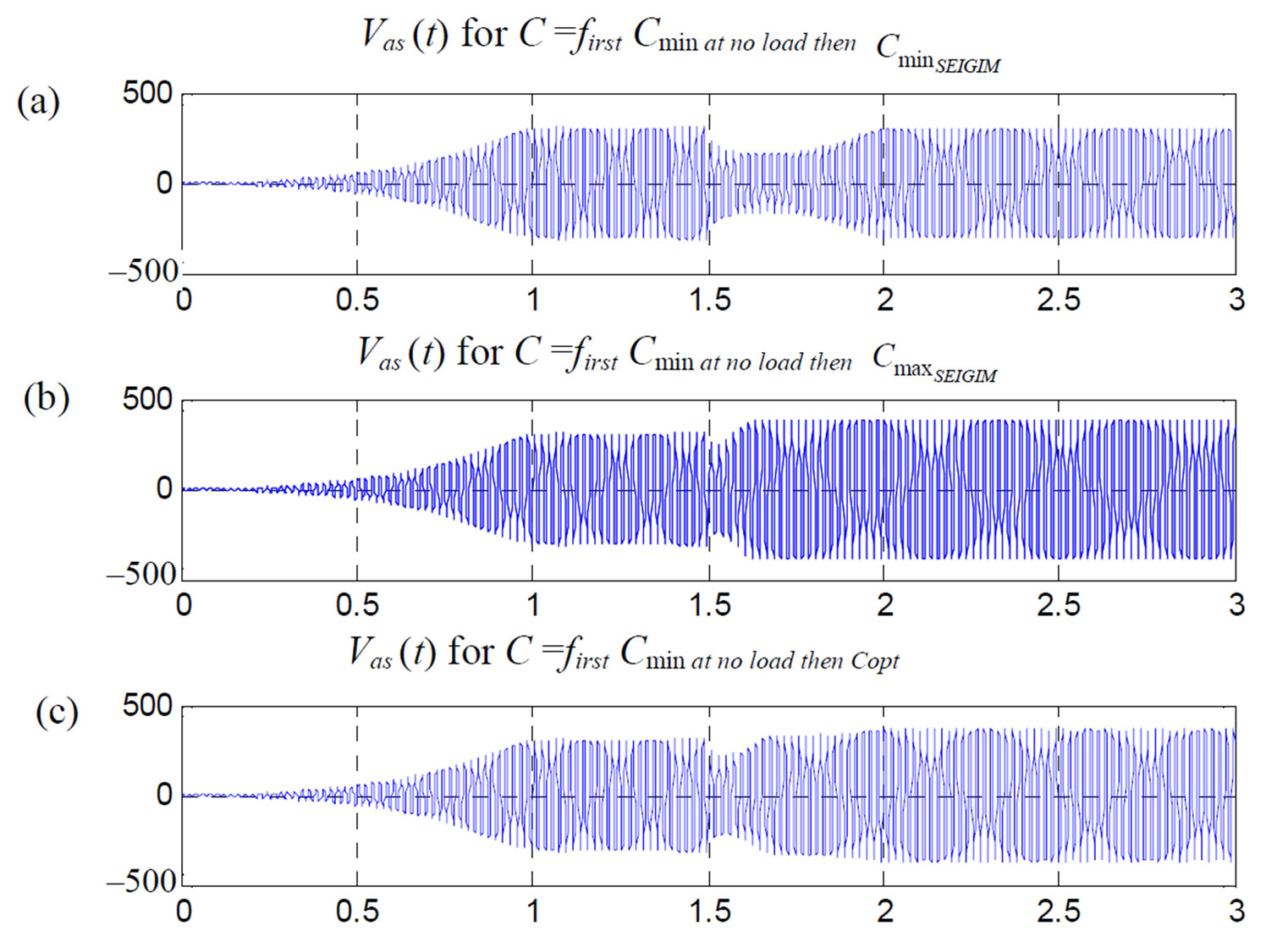
Figure 10.  Variation with time at different modes of operation.
Variation with time at different modes of operation.

Figure 11.  variation with time at different modes of operation.
variation with time at different modes of operation.
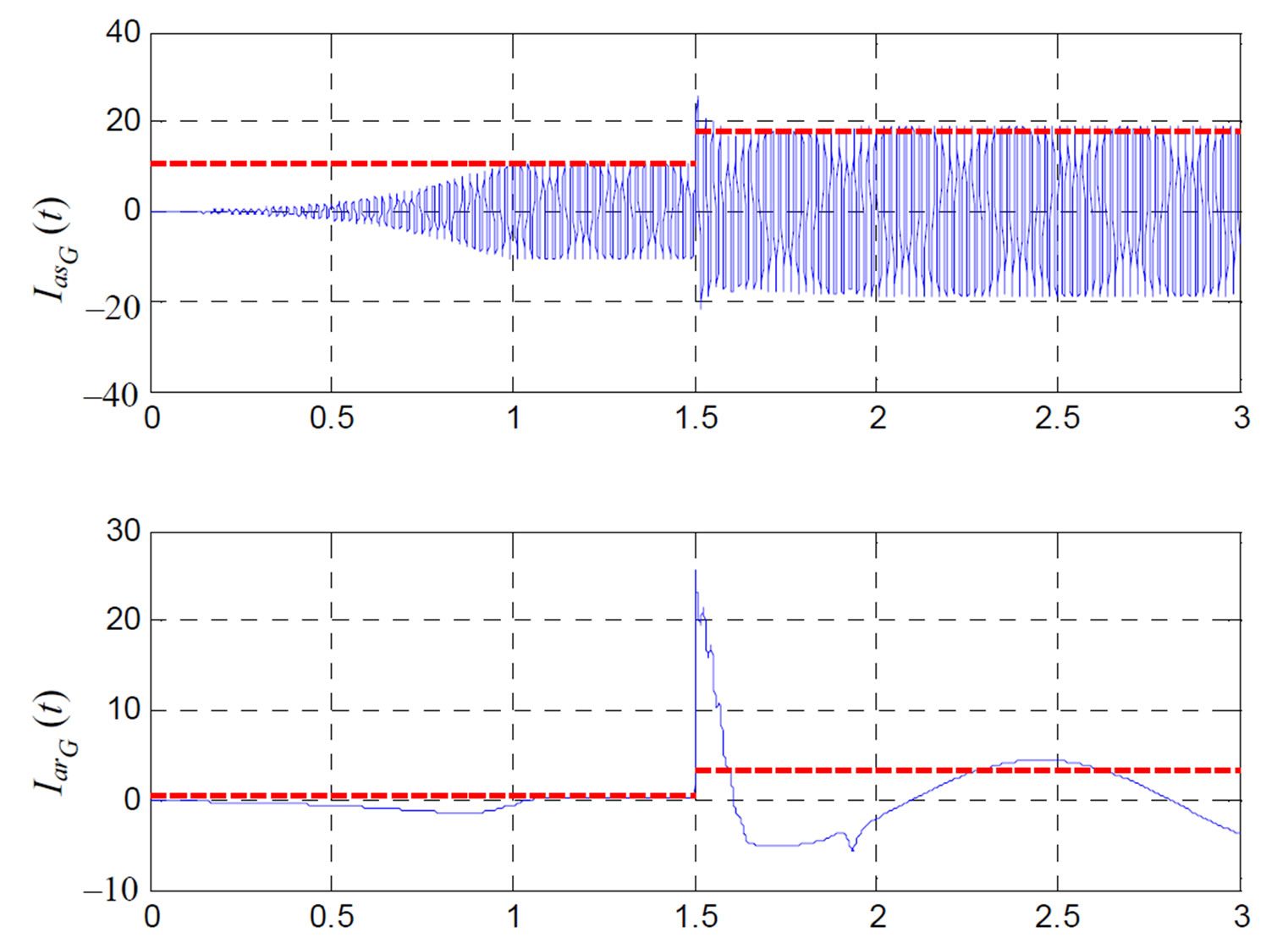
Figure 12.  and
and  variation with time at adequate operation mode.
variation with time at adequate operation mode.
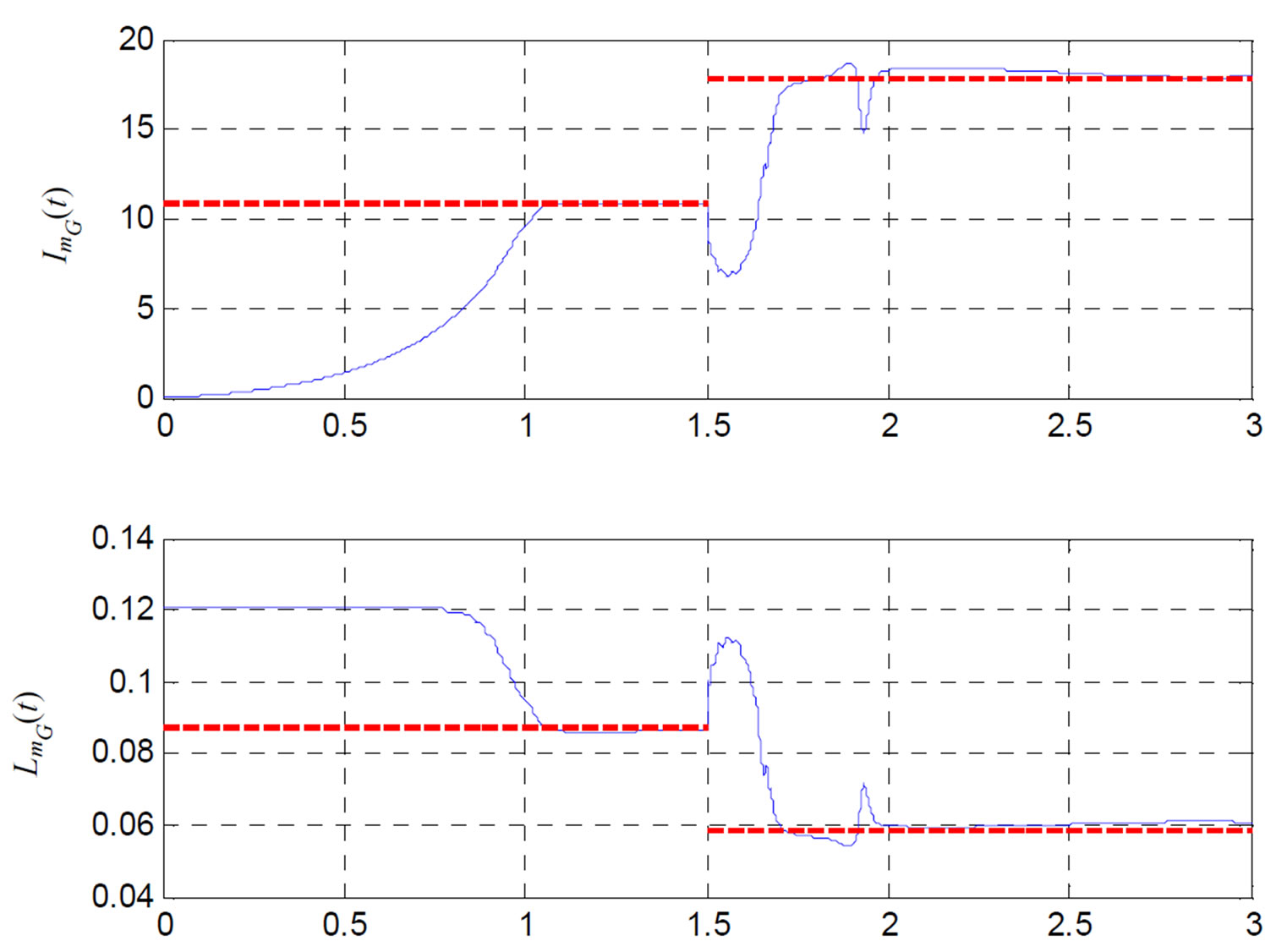
Figure 13. 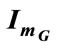 and
and  variation with time at adequate operation mode.
variation with time at adequate operation mode.
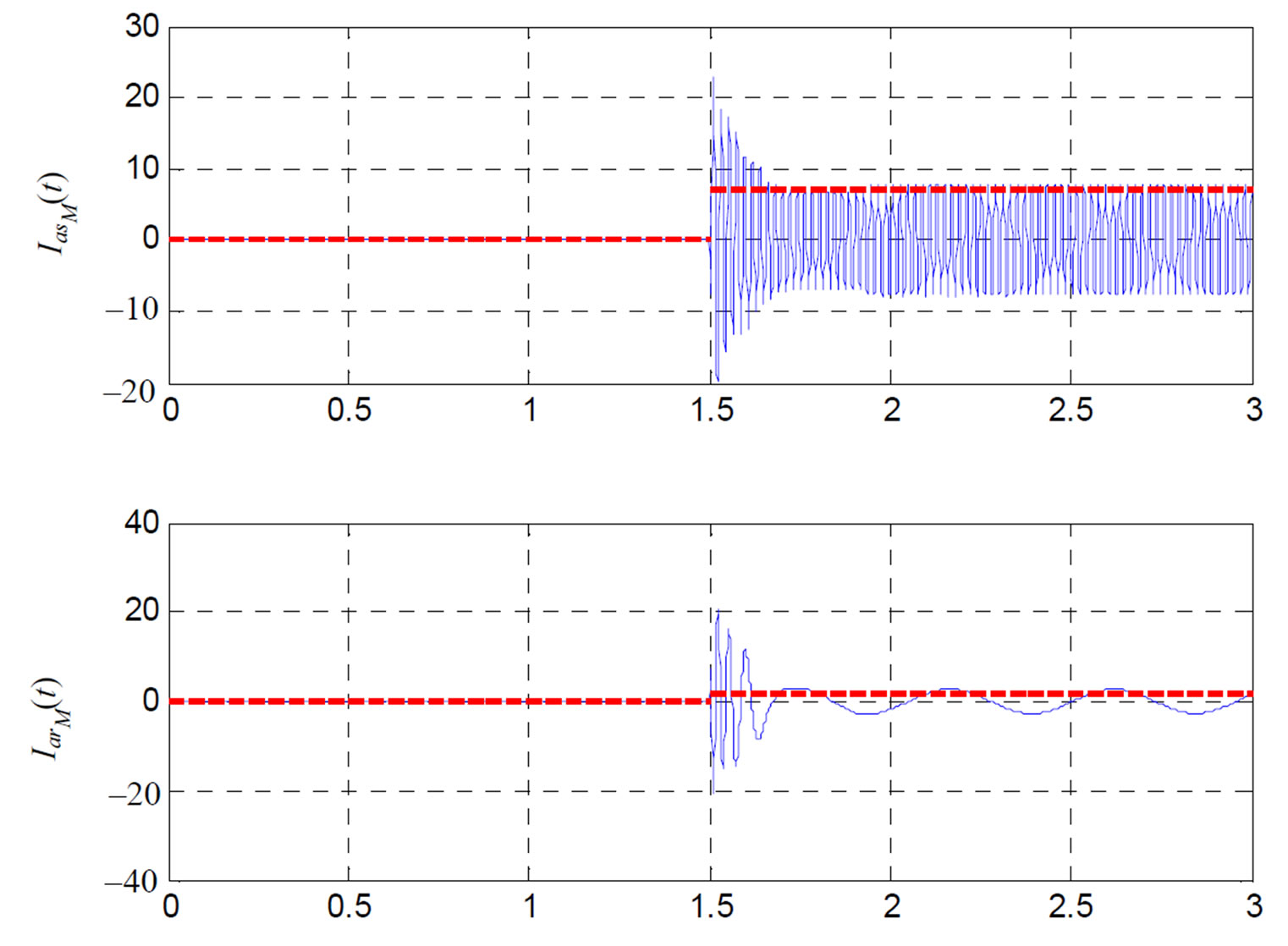
Figure 14. 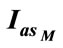 and
and 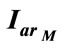 variation with time at adequate operation mode.
variation with time at adequate operation mode.
(a)-10(c)). The self excitation process is consequently established and maintained.
For the same scenario of capacitance values, the  variation as a function of time is presented (Figure 11) and their steady state values during the second phase noted by
variation as a function of time is presented (Figure 11) and their steady state values during the second phase noted by ,
,  ,
,  are examined. It shows that
are examined. It shows that  and
and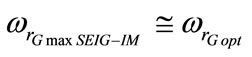 .
.
This proves the justification of the choice of the value  calculated in the static state steady.
calculated in the static state steady.
Therefore, the appropriate operation mode of SEIG is that for which  is equal to
is equal to  during the first stage and equal to
during the first stage and equal to 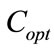 during the second stage. Figures 12-14 show the variation of
during the second stage. Figures 12-14 show the variation of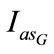 ,
,  ,
, 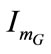 ,
, 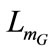 ,
,  and
and 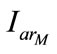 as a function of time. The continuous line curves are the curves obtained in dynamic mode and those in broken line are obtained in static mode. Good agreements between the two results are confirmed.
as a function of time. The continuous line curves are the curves obtained in dynamic mode and those in broken line are obtained in static mode. Good agreements between the two results are confirmed.
5. Conclusions
In order to optimize the quantity of the pumped water, an effect of an excitation capacitor on the steady state behaviour of the SEIG-IM plant is studied to enable selection of optimal capacitance value for a giving wind rotor. A steady state analysis is examined using the nodal admittance concept and the per phase equivalent circuit which represent the model of this plant. The transient performance of SEIG-IM system is moreover presented and examined to determine the suitable operation mode of this system.
REFERENCES
- A. M. Omer, “Energy, Environment and Sustainable Development,” Renewable and Sustainable Energy Reviews, Vol. 12, No. 9, 2008, pp. 2265-2300. doi:10.1016/j.rser.2007.05.001
- B. G. Ziter, “Electric Wind Pumping for Meeting OffGrid Community Water Demands,” Guelph Engineering Journal, Vol. 2, 2009, pp. 14-23.
- M. S. Miranda, R. O. Lyra and S. R. Silva, “An Alternative Isolated Wind Electric Pumping System Using Induction Machines,” IEEE Transactions on Energy Conversion, Vol. 14, No. 4, December 1999, pp. 1611-1616. doi:10.1109/60.815113
- N. H. Malik and A. H. AI-Bahrani, “Influence of the Terminal Capacitor on the Performance Characteristics of a Self Excited Induction Generator,” IEE Proceedings C: Generation, Transmission and Distribution, Vol. 137, No. 2, March 1990, pp. 168-173.
- K. Idjdarene, D. Rekioua, T. Rekioua and A. Tounzi, “Vector Control of Autonomous Induction Generator Taking Saturation Effect into Account,” Energy Conversion and Management, Vol. 49, No. 10, 2008, pp. 2609- 2617. doi:10.1016/j.enconman.2008.05.014
- R. C. Bansal, “Three-Phase Self-Excited Induction Generators: An Overview,” IEEE Transactions on Energy Conversion, Vol. 20, No. 2, June 2005, pp. 292-299. doi:10.1109/TEC.2004.842395
- G. K. Singh, “Self-Excited Induction Generator Research—A Survey,” Electric Power Systems Research, Vol. 69, No. 2-3, 2004, pp. 107-114. doi:10.1016/j.epsr.2003.08.004
- M. H. Haque, “Comparison of Steady State Characteristics of Shunt, Short-Shunt and Long-Shunt Induction Generators,” Electric Power Systems Research, Vol. 79, No. 10, 2009, pp. 1446-1453.
- doi:10.1016/j.epsr.2009.04.017
- K. A. Nigim, M. M. A. Salama and M. Kazerani, “Identifying Machine Parameters Influencing the Operation of the Self-Excited Induction Generator,” Electric Power Systems Research, Vol. 69, No. 2-3, 2004, pp. 123-128. doi:10.1016/j.epsr.2003.08.003
- I. M. Katiniotis, M. G. Ioannides and P. G. Vernados, “Operation of Induction Generator in the Magnetic Saturation Region as a Self-Excited and as a Double Output System,” Journal of Materials Processing Technology, Vol. 161, No. 1-2, 2005, pp. 263-268. doi:10.1016/j.jmatprotec.2004.07.034
- L. Wang and Ch.-H. Lee, “A Novel Analysis on the Performance of an Isolated Self Excited Induction Generator,” IEEE Transactions on Energy Conversion, Vol. 12, No. 2, June 1997, pp. 109-117. doi:10.1109/60.629692
- M. H. Salama and P. G. Holmes, “Transient and steady State Load Performance of a Stand Alone Self Excited Induction Generator,” IEE Proceedings, Electric Power Application, Vol. 143, No. 1, January 1996, pp. 1350- 2352. doi:10.1049/ip-epa:19960002
- B. Singh, L. Shridhar and C. S. Jha, “Transient Analysis of Self-Excited Induction Generator Supplying Dynamic Load,” Electric Machines And Power Systems, Vol. 27, No. 9, 1999, pp. 941-954. doi:10.1080/073135699268795
- S. Sallem, M. Chaabene and M. B. A. Kamoun, “Energy Management Algorithm for an Optimum Control of a Photovoltaic Water Pumping System,” Applied Energy, Vol. 86, No. 12, 2009, pp. 2671-2680. doi:10.1016/j.apenergy.2009.04.018
- R. J. Harrington and F. M. M. Bassiouny, “New Approach to Determine the Critical Capacitance for SelfExcited Induction Generators,” IEEE Transactions on Energy Conversion, Vol. 13, No. 3, September 1998, pp. 244-249. doi:10.1109/60.707603
Nomenclature
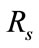 ,
, : Stator and rotor resistances,
: Stator and rotor resistances,
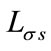 ,
, : Stator and rotor leakage inductances,
: Stator and rotor leakage inductances,
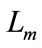 : Cyclic stator mutual inductance,
: Cyclic stator mutual inductance,
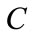 : Excitation capacitor,
: Excitation capacitor,
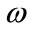 : Stator angular frequency,
: Stator angular frequency,
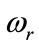 : Rotor electrical angular speed,
: Rotor electrical angular speed,
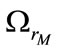 : Mechanical motor speed,
: Mechanical motor speed,
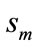 : Induction motor slip,
: Induction motor slip,
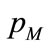 : Number of poles pairs of induction motor,
: Number of poles pairs of induction motor,
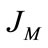 : Inertia moment of IM
: Inertia moment of IM
 : Imaginary operator
: Imaginary operator
Superscript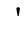 denotes the transformed rotor quantities based on the stator.
denotes the transformed rotor quantities based on the stator.
Indices 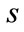 and
and 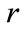 stand for stator and rotor respectively, while
stand for stator and rotor respectively, while 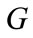 and
and  stand for induction generator and induction motor respectively.
stand for induction generator and induction motor respectively.

