Energy and Power Engineering
Vol.06 No.11(2014), Article ID:50747,17 pages
10.4236/epe.2014.611034
The Influence of Radial Area Variation on Wind Turbines to the Axial Induction Factor
Kedharnath Sairam, Mark G. Turner
School of Aerospace Systems, University of Cincinnati, Cincinnati, USA
Email: kdbeggar@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 July 2014; revised 20 August 2014; accepted 10 September 2014
ABSTRACT
Improvements in the aerodynamic design will lead to more efficiency of wind turbines and higher power production. In the present study, a 3D parametric gas turbine blade geometry building code, 3DBGB, has been modified in order to include wind turbine design capabilities. This approach enables greater flexibility of the design along with the ability to design more complex geometries with relative ease. The NREL NASA Phase VI wind turbine was considered as a test case for validation and as a baseline by which modified designs could be compared. The design parameters were translated into 3DBGB input to create a 3D model of the wind turbine which can also be imported into any CAD program. Design modifications included replacing the airfoil section and modifying the thickness to chord ratio as a function of span. These models were imported into a high-fidelity CFD package, Fine/TURBO by NUMECA. Fine/TURBO is a specialized CFD platform for turbo-ma- chinery analysis. A code-geomturbo was used to convert the 3D model of the wind turbine into the native format used to define geometries in the Fine/TURBO meshing tool, AutoGrid. The CFD results were post processed using a 3D force analysis code. The radial force variations were found to play a measurable role in the performance of wind turbine blades. The radial component of the blade surface area as it varies in span is the dominant contributor of the radial forces. Through the radial momentum equation, this radial force variation is responsible for creating the streamline curvature that leads to the expansion of the streamtube (slipstream) that is responsible for slowing the wind velocity ahead of the wind turbine leading edge, which is quantified as the axial induction factor. These same radial forces also play a role in changing the slipstream for propellers. Through the design modifications, simulated with CFD and post-processed appropriately, this connection with the radial component of area to the radial forces to the axial induction factor, and finally the wind turbine power is demonstrated. The results from the CFD analysis and 3D force analysis are presented. For the case presented, the power increases by 5.6% due to changes in airfoil thickness only.
Keywords:
Wind Energy, Axial Induction Factor, Radial Area Variation, Wind Power, 3DBGB, Force Analysis

1. Introduction
Wind energy is one of the fastest growing energy sectors today. Apart from being a very promising source of energy, it also has other advantages. It is a source of green power and hence is a very critical part of the solution to the global climate change crisis. It is affordable and cost effective. The cost of manufacturing and monitoring wind turbines has reduced drastically over the last few decades owing to advancements in manufacturing tech- nology. It improves economic development by providing a range of job opportunities in the communities where the wind farms are located. It is a sustainable source of energy and widely available [1] .
The power output of a wind turbine is directly related to the swept area of the rotors [2]
 (1)
(1)
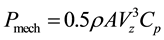 (2)
(2)
where 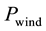 is the power available in the kinetic energy of the wind.
is the power available in the kinetic energy of the wind.
The power coefficient depends on the overall aerodynamic and mechanical efficiency of the wind turbine design. Therefore, the power output of a wind turbine at a prescribed wind velocity can be improved by in- creasing the swept area of the rotor. However, not all wind turbine installation sites are suitable for large rotors and a large part of the capital cost is related to the rotor size. One of the key aspects of wind turbine design is the ability to extract as much energy from the wind as possible and reducing aerodynamic and mechanical losses to a minimum.
A general illustration of 2D wind turbine aerodynamics is given in Figure 2. Wind turbine design nomen- clature is provided in Figure 3 and conventional turbine nomenclature is provided in Figure 4. When the on-coming wind hits the wind turbine blade, a low pressure field is created on the suction side of the airfoil and a high pressure field is created on the pressure side of the airfoil. This creates a resultant force to act on the blade which can be represented as components of the force that are normal to each other i.e the lift and drag on the airfoil. The drag force is small compared to the lift force at the high reynold’s number of modern wind turbines. This lift causes the blade to rotate.
Current wind turbine design approaches are based on the Blade-Element-Momentum theory, a 2D method which is explained in detail in [2] . 2D force analysis is a great way to understand the fundamentals of aerody- namics. However, in reality, complex 3D effects occur which need to be analyzed in order to optimize the blade design. A post-processing code was developed for 3D force analysis on the blade. This post-processing capa-
Figure 1. Actuator disc model [3] .
Figure 2. Wind turbine aerodynamics in 2d [4] .
Figure 3. Wind turbine nomenclature [4] .
Figure 4. Conventional turbine nomenclature [4] .
bility allows the interpretation of forces relevant to a wind turbine. The effect of radial force variation on the performance of the blade was discovered to be significant. The radial forces have been found to act as a main driver for the stream tube area expansion. New blades were designed to further explore the effect of radial forces in detail by manipulating the geometry.
Access to the 3D parametric blade geometry builder-3DBGB [5] -[7] , a gas turbine blade geometry generation tool, proved to be a useful way to approach the design of wind turbines with complex geometries. Using the built-in airfoil definition, tip-offset, sweep and rake options, it was possible to manipulate the rotor geometry. CAD models of the blade were created using the output from 3DBGB. The design was then analyzed using a 3D CFD package-Fine/Turbo. Post-processing was carried out by the 3D force analysis code-Calc- PdA and other tools. The NREL Phase VI wind turbine was used as a starting point because of the availability of detailed design and analysis data [8] .
Very little investigation has been done on manipulating the geometry to modify the radial forces on the blades. This paper aims to explore improvements in performance due to thickness to chord ratio variation of not only wind turbines, but also propellers and other turbo-machinery applications as well. Wind turbine geometry de- finition using 3DBGB and 3D CFD analysis using Fine/Turbo are explained in subsequent sections. A detailed explanation of the 3D force analysis code is provided. The results and comparison for the wind turbine test cases are presented and effect of radial area variation on wind turbine rotor blades is explained.
2. Wind Turbine Geometry Definition Using 3DBGB
3DBGB [5] -[7] is a blade geometry generation tool that uses a parametric approach to design blades for turbomachinery applications. Due to its parametric nature, a wide range of blades can be designed with relative ease. 2D airfoil sections are created using geometric and aerodynamic input quantities. The sections are stacked in a 3D cylindrical space and are transformed to cartesian space. This can be imported into any CAD package to create 3D solid models. Conventional wind turbines are stacked radially, but other input can be used to define a stacking axis and location on the blade for stacking. The geometry builder is also capable of creating complex geomtries such as bent tips and split tips with minimum change to the inputs.
2.1. Blade Design Process
3DBGB uses the input file “3dbgbinput.dat” to extract the input parameters and create 3D sections. The number of blades, scaling factor and number of streamlines are specified in the first few lines of the input file. A switch to use non-dimensional actual chord values is available to enable reverse engineering of known blades. At each streamline the blade inlet and outlet angles, relative mach number at inlet, non-dimensional actual chord, thick- ness to chord ratio, incidence, deviation and secondary flow angle are specified. The blade stagger angle can be input through the inlet and outlet leading edge and trailing edge angles.
3DBGB has the capability to generate a variety of airfoils. Due to its parametric nature it is easy to define different airfoils at different sections which makes the design process highly flexible. Presently, the code has the capability to create circular sections, NACA 4-digit airfoils, NREL S809 airfoils and the default mixed camber airfoil. New airfoils can also be included in the code.
3. 3D CFD Analysis
FINE/TurboTM is a Computational Fluid Dynamics (CFD) analysis tool from NUMECA International [9] . It stands for Flow Integrated Environment and it is a complete CFD package which includes grid generation, flow solver and post-processing capabilities. FINE/Turbo is specialized to simulate internal, rotating and turboma- chinery flows for all types of fluids. The package has a fully hexahedral and highly automated grid generation module AutoGridTM. The package uses a 3D Reynolds Averaged Euler and Navier Stokes flow solver EURANUS. CFViewTM is a post-processing module which is also part of the package.
3.1. Grid Setup
The grid generation module, AutoGrid, provides the option of either importing and linking a CAD file or importing a “.geomturbo” file, which is the native blade section file format. The blade generation code 3DBGB has the capability to output the blade geometry in the “.geomturbo” file format, which makes importing the blade geometry simple as it initializes the grid parameters and geometry definition. The built-in wind turbine wizard mode in AutoGrid was used to create good grids with the appropriate blade topologies. Figure 5 shows the grid created using AutoGrid. A complete description of all the parameters and definitions can be found in the NUMECA User Manuals [10] .
Figure 5. 3D grid.
3.2. Flow Setup and Solution
The Fine/Turbo flow solver module is an intuitive platform to set up the flow properties and to run a simulation. Once the boundary conditions are appropriately assigned using the IGG module, the path to the IGG file is specified in the flow solver module and the flow parameters are specified. The parameters used for the wind turbine case are given below.
• *Configuration
--Fluid Model-Air-(perfect gas)
--Flow Model-Characteristics of the flow:
* -Time Configuration-Steady
* -Mathematical Model
• Turbulent Navier-Stokes
• Spalart-Allmaras Turbulence Model
* -Low Speed Flow-
--Rotating Machinery-72 RPM
• *Optional Models—Abu-Ghanam-Shaw Transition Model
• *Boundary Conditions—The boundary condition already generated in Autogrid are available for additional input definition.
Once the flow properties are set, the flow solver EURANUS can be started and the convergence can be mo- nitored. Fine/Turbo also provides the option of running the solution in batch processing mode. The conver- gence history can be viewed graphically for the global residuals, torque, efficiency and axial thrust. Using the CFView module, the solution can be post-processed to visualize the flow feild properties. Figure 6 shows the 3D static pressure contour for the NREL blade using CFView. Further post-processing was done using Asgard. Asgard is a collection of visualization/post-processing tools. The asgard library serves as the backbone for file manipulations, calculations, and feature extractions.
4. 3D Force Analysis
The flow field around a wind turbine is complex and no matter how close a 2D approximation is, it will still be innacurate and fail to account for all the details. This was the reason a code was developed using MatLab for 3D force analysis. From the CFD results, the data from each grid point on the blade was extracted using Asgard. This data was processed to arrive at the aerodynamic forces acting on elemental slabs of the wind turbine blade and these forces were integrated over the span to arrive at the global force, torque and power output of the blade.
4.1. Code Formulation
Using the data extracted from Asgard, the blade was divided into the individual sections. Each section and the section above it in the radial direction were treated as a 3D slab. Figure 7 shows two consecutive 3D slabs. Each
Figure 6. 3d Static pressure contour–pressure, side and suction side-nrel blade.
Figure 7. 3D slabs created using CFD data.
slab is divided into elemental areas. Points A,B,C and D enclose one such area. The static pressure at each point is known. The average static pressure acting on the elemental area is found.
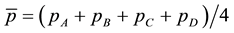 (3)
(3)
The area vector of the elemental area is found by using the diagonal vectors which is then multiplied with the average pressure to obtain the force  acting on the elemental area. The resultant force
acting on the elemental area. The resultant force 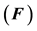 acting on the slab is the summation of the forces acting on all the “n” elemental areas on the slab.
acting on the slab is the summation of the forces acting on all the “n” elemental areas on the slab.
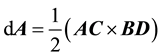 (4)
(4)
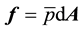 (5)
(5)
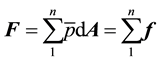 (6)
(6)
Figure 8 shows two slabs with diagonal vectors and force vectors on each elemental area. The cartesian force vectors are transformed into cylindrical force vectors. The position vector for the transformation is taken as the centroid of the slab. The centroid is found using an open source MatLab function-Polygeom [11] .
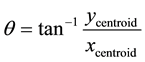 (7)
(7)
Figure 8. Diagonal vectors and force vectors on, a slab.
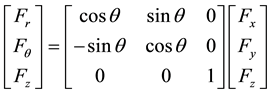 (8)
(8)
The product of the tangential force and the local radius gives the torque of the slab. Summing all the torques yeilds the global torque of the blade. The product of the global torque and the rotational speed of the blade gives the power output output of the blade which can be multiplied with the total number of blades to give the total power output of the wind turbine.
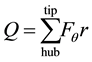 (9)
(9)
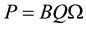 (10)
(10)
It should be noted that shear forces are not taken into account in this analysis as they were found to be very negligible owing to the high Reynold’s number.
5. Results and Comparison
The 3D force analysis was carried out on the NREL Phase VI blade and used as a baseline. CFD results for the NREL blade predicted a power output of 4.8 kilowatts for a Vz of 7 m/s. This was validated using the NREL design report [8] as seen in Figure 9 which produced a power output of 4.8 kilowatts at 7 m/s in a test as interpreted from the graph. In order to analyze the effect of the radial area variation in great detail, the NREL blade’s S809 airfoil was substituted with a NACA 2420 airfoil since this was a close approximation to the S809 airfoil. The dependence of the radial forces associated with the blade on the radial component of the cross sectional area can be seen mathematically through the integral form of the radial momentum equation.

The third term on the left hand side is the radial force term and “rd
The NACA 2420 airfoil was found to be a very close approximation to the S809 airfoil in both thickness and lift coefficient characteristics. The difference in the lift coefficient is within a tolerable margin in the angle of attack range from 0 to 7 degrees for the S809 and NACA 2420 airfoils, which is the region where the effective angle of attack lies for the blade. The maximum difference in 
Figure 9. NREL power curve [12] .
The addition of the NACA 4-digit airfoil generation capability in the 3DBGB code provided a tremendous range of airfoil sections that could be included in the design. The thickness to chord ratio of the airfoils is the key parameter that is used to manipulate the radial component of the surface area. Figure 10 shows the lift coefficient characteristics obtained using XFOIL [4] of a few NACA airfoils that have been used in the blade design. It can be seen that they all have very similar 

5.1. NACA 2420 vs. NACA 2420-2404
The NACA 2420-2404 blade consists of the NACA 2420 airfoil till 50% span and then gradually decreases to NACA 2404 at the tip as shown in Figure 11. Due to the greater change in the radial component of the area, the NACA 2420-2404 blade has higher radial forces acting on the blade than the NACA 2420 blade. The jump in the radial force at 50% span for the NACA 2420-2404 blade can be clearly seen in Figure 12. The tangential forces, axial forces and torque are also greater for the NACA 2420-2404 blade than the NACA 2420 blade as seen in Figure 13-15.
Figure 12 shows the radial force comparison between the NACA 2420 and NACA 2420-2404 blades using gauge pressure instead of static pressure. This is done by substituting the pressure term in the force equation with 



Figure 10. Lift coefficient vs. Angle of attack-NACA series.
Figure 11. Cross sectional area vs. span.
Figure 12. Radial force using gauge pressure vs. span.
So the axial induction factor for the NACA 2420-2404 blade is 9.8% higher than the NACA 2420 blade. The mass flow rate is constant through a streamtube for each design. From the actuator disc theory [2] shown in Figure 1, subscript “1” corresponds to the station far upstream and subscript “2” corresponds to the station just in front of the leading edge.


The density is essentially constant and 

Figure 13. Tangential force vs. span.
Figure 14. Axial force vs. span.
Figure 15. Torque vs. span.


The subtle and gradual radial area variation between the NACA 2420 and NACA 2420-2404 blades has resulted in a 1.96% decrease in the streamtube area far upstream of the blade. This area change results in a lower
Figure 16. Area averaged vz in front of blade vs. span.
Figure 17. Axial induction factor vs. span.
Figure 18. Effective angle of attack vs. span.
Vz in front of the blade, increasing the effective angles of attack over the span of the blade and directly contri- butes to the increase in the tangential forces acting on the blade. The increase in tangential forces ultimately improves the power output of the blade.



Figure 19. Lift coefficient vs. span.

Theoretically, the power output of the NACA 2420-2404 blade is 5.661% more than the NACA 2420 blade. The power output of the blades was calculated from the torque.


The NACA 2420 blade has a power output of 6.0117 Kilo Watts which is 25.8% more than the NREL original blade. This increase in the power output is due to the slightly better 
6. Effect of Radial Area Variation
In the actuator disc model discussed in [2] and shown in Figure 1, the wind velocity in stations 2 and 3, 





The radial momentum equation can be expressed in terms of the streamline curvature, using the streamline curvature approach as outlined in [12] , as follows.

L.H. Smith, Jr. derived an equation to describe the radial variation of circumferentially averaged flow properties inside a turbomachinery blade row [14] . Circumeferential averaging of a flow property “x” is defined as

where 





The first term on the right hand side of Equation (27) is the desired radial gradient of the average pressure. The second term is related to the radial component of the blade force on the fluid and the last term is attributed to a blockage effect. Smith [14] goes on to state that the last term vanishes when the pressure varies linearly in the 


When the lean angle 

Figure 20 shows the comparison of the first term in Equation (27), the radial gradient of the circumferentially
averaged pressure, between the NACA 2420 and NACA 2420-2404 blades. The 
2420-2404 blade is lower than the NACA 2420 blade over most of the span, especially from 40% - 60% of the span and from 82% - 100% span.
The third term in Equation (27), the blockage effect term, is compared between the NACA 2420 and the NACA 2420-2404 blades in Figure 21. It is slightly higher for the NACA 2420-2404 blade than the NACA 2420 blade at mid-span. From 62% - 100% span, it is lower for the NACA 2420-2404 blade than the NACA 2420 blade.
Figure 20. Radial pressure gradient term in Equation (9.14) 
Figure 21. Third term in Equation (9.14) 
The difference between the two cases is the cause for the difference in the circumferencial averaged radial pressure gradient. The streamline curvature is directly related to the circumferentially averaged radial pressure gradient; hence, the NACA 2420 and NACA 2420-2404 blades have different streamline curvatures. The NACA 2420-2404 blade is able to bend the streamlines more than the NACA 2420 blade, thereby increasing the streamtube area expansion and reducing the wind speed ahead of the blade more effectively. This enables the NACA 2420-2404 blade to extract more energy from the wind and perform better than the NACA 2420 blade.
In order to get the circumferential average streamtube radius at the tip, thirty streamlines were spawned, equi-distant from each other, on a line between the leading edge and trailing edge of the two blades for the NACA 2420 and NACA 2420-2404 cases using Asgard. A comparison of the thirty streamtubes between the NACA 2420 and NACA 2420-2404 blades can be seen in Figure 22. The average streamtube radius for the NACA 2420 blade and NACA 2420-2404 blade are shown in Figure 23 and Figure 24. They are embedded on their respective azimuthal averaged static pressure contours. It can be seen how the streamlines are bent more for the NACA 2420-2404 blade at the tip than the NACA 2420 blade. The area ratio is the streamtube area of the NACA 2420-2404 blade over the streamtube area of the NACA 2420 blade. Figure 25 and Figure 26 show the streamtube area and area ratio respectively.
The blade lies between Z = 47.7 meters and Z = 48 meters. The upstream streamtube area of the tip streamlines for the NACA 2420-2404 blade is slightly lower than the NACA 2420 blade. When the streamlines reach the blade tip, the difference in area grows large. The NACA 2420-2404 blade is able to reduce the wind velocity and increase the streamtube area at the blade more than the NACA 2420 blade; thereby, extracting more kinetic energy from the wind.
The average axial induction factor of the NACA 2420 blade is 0.1637 and the average axial induction factor of the NACA 2420-2404 blade is 0.1798. Theoretically, the maximum possible axial induction factor is 0.3333 according to Betz [13] . From Figure 26, it can be seen that the area ratio far upstream of the blade is approxi- mately 0.98. This area ratio can be related to the average axial induction factor through Equation (16) and the results are very similar. The axial induction factor depends on the streamtube area which, in turn, depends on how much the streamlines are bent in front of the blade. Higher radial area variation on the blade facilitates this bending of the streamlines by creating a higher radial pressure gradient. The lowering of Vz in front of the blade improves the effective angles of attack over the span; thereby increasing the lift coefficients over the span. As a result, the tangential forces acting on the blade are improved; hence, the power output is higher. As shown in Equation (17) and Equation (21), a 1.96% decrease in the streamtube area far upstream of the blade causes the power to increase by 5.661%. The power output results from CFD analysis show that the NACA 2420-2404 blade has an output that is 6.8690% higher than that of the NACA 2420 blade.
7. Conclusion and Future Work
Methods to improve the performance of wind turbines have been explored. 3D CFD analysis was carried out on
Figure 22. Streamtube radius vs. Z at tip-naca 2420 and naca 2420-2404-30 streamlines.
Figure 23. Average streamtube radius vs. Z at tip-naca 2420.
Figure 24. Average streamtube radius vs. Z at tip-naca 2420-2404.
an NREL phase VI wind turbine. 3D analysis of the forces acting on the blade established the magnitude of the radial force acting on the blade to be much larger than the tangential and axial forces. The impact of radial area variation on the performance of the blade was explored using the NACA four digit airfoil series. The thickness to chord ratio was manipulated over the span of the blade to explore its effect.
Figure 25. Average streamtube radius vs. Z at tip-NACA 2420 and NACA 2420-2404.
Figure 26. Average streamtube area ratio vs. Z at tip-NACA 2420 and NACA 2420-2404.
The NACA 2420-2404 blade has been found to have the best performance. The key findings of this research work are as follows:
• *The radial component of the surface area of the blade is a contributor to the magnitude of the radial forces acting on the blade.
• *The radial pressure gradient is responsible for bending the streamlines.
• *For wind turbines which operate at low wind speeds, this circumferentially averaged radial pressure gradient term depends on the blockage effect.
• *The axial induction factor depends on the streamtube area which, in turn, depends on how much the streamlines are bent by the blade.
• *The axial induction factor influences the effective angle of attack seen by the blade sections.
• *An increase in the streamtube area by 1.96% results in an increase in power output by 5.661%.
• *The NACA 2420-2404 blade has a power output that is 6.8690% higher than the NACA 2420 blade.
Improved models need to be developed between the radial variation of the cross-sectional area and the axial induction factor. This will aid in desigining wind turbine blade geometries with high axial induction factors to extract the maximum possible power from the wind. The 3D force analysis code developed for this thesis can be used for a wide range of applications. The findings presented in this paper are not only restricted to wind turbines but can also be applied to propellers, transonic fans, open rotors and other turbomachinery applications. A highly detailed version of this research can be found in [15] .
Acknowledgements
A special thanks to Kiran Siddapaji and Soumitr Dey for their help and brainstorming sessions for my research. Thanks to Rob Ogden for helping me with many license and Linux issues. I would like to thank Robert Knapke, Marshall Galbraith and Andy Schroder for their support and help. I would also like to thank the NUMECA support team (Roque Lopez and Autumn Fjeld ) for their timely help with Fine Turbo trouble-shooting.
References
- Appalachian State University-North Carolina Wind Energy. www.wind.appstate.edu
- Manwell, J.F. and McGowan, J.G. and Rogers, A.L. (2002) Wind Energy Explained: Theory, Design and Application of Wind Energy. 1st Edition, John Wiley and Sons, Inc., Hoboken.
- Dey, S. (2011) Wind Turbine Blade Design System-Aerodynamic and Structural Analysis. Master’s thesis, University of Cincinnati, Cincinnati.
- Drela, M. and Youngren, H. XFOIL-Subsonic Airfoil Development System. http://web.mit.edu/drela/Public/web/xfoil/
- Park, K., Turner, M.G., Siddappaji, K. and Dey, S. and Merchant, A. (2011) Optimization of a 3-Stage Booster Part 1: The Axisymmetric Multi-Disciplinary Optimization Approach to Compressor Design. ASME Proceedings, Paper No. GT2011-46569, 1413-1422.
- Siddappaji, K. (2012) Parametric 3D Blade Geometry Modeliing Tool for Turbomachinery Systems. Master’s Thesis, University of Cincinnati, Cincinnati.
- Siddappaji, K., Turner, M.G., Dey, S., Park, K. and Merchant, A. (2011) Optimization of a 3-Stage Booster-Part 2: The Parametric 3D Blade Geometry Modeling Tool. ASME Proceedings, Paper No. GT2011-46664, 1431-1443.
- Giguere, P. and Selig, M.S. (1999) Design of a Tapered and Twisted Blade for the NREL Combined Experiment Rotor. Technical report, NREL/SR-500-26173. http://dx.doi.org/10.2172/750919
- Numeca. www.numeca.com
- Numeca User Manuals. www.numeca.com
- http://www.mathworks.com/matlabcentral/fileexchange/319-polygeom-m
- Novak, R.A. (1967) Streamline Curvature Computing Procedures for Fluid-Flow Problems. Journal of Engineering for Gas Turbines and Power, 89, 478-490.
- Betz, A. (1926) Windenergie und ihre ausnutzung durch wind-muhlen: Vandenhoeckund ruprecht.
- Smith Jr., L.H. (1966) The Radial-Equilibrium Equation of Turbomachinery. Journal of Engineering for Gas Turbines and Power, 88, 1-12.
- Sairam, K. (2013) The Influence of Radial Area Variation on Wind Turbines to the Axial Induction Factor. Master’s Thesis, University of Cincinnati, Cincinnati.
Nomenclature








