Communications and Network
Vol. 4 No. 2 (2012) , Article ID: 19100 , 5 pages DOI:10.4236/cn.2012.42019
The Tight Bound for the Number of Pilots in Channel Estimation for OFDM Systems
Electrical Engineering Department, Shahed University, Tehran, Iran
Email: *mimani@shahed.ac.ir
Received February 24, 2012; revised March 28, 2012; accepted April 20, 2012
Keywords: Doppler Frequency Shift; Second Order Statistics; Channel Estimation; Pilot; OFDM
ABSTRACT
Coherent detection in OFDM systems requires accurate channel state information (CSI) at the receiver. Channel estimation based on pilot-symbol-assisted transmissions provides a reliable way to obtain CSI. Use of pilot symbols for channel estimation, introduces overhead and it is desirable to keep the number of pilot symbols as minimum as possible. This paper introduces a new tight bound for the number of pilots in channel estimation using adaptive scheme in OFDM systems. We calculate the minimum number of necessary pilots using two approaches. The first approach for the number of pilots is obtained based on Doppler frequency shift estimation and the second approach is acquired based on channel length estimation using second order statistics of received signal. Finally we obtain the tight bound for the number of pilots using attained values.
1. Introduction
Orthogonal frequency division multiplexing (OFDM) represents a valid choice for a variety of wireless applications since it has been shown to outperform single-carrier schemes especially in high data rate applications [1]. To correctly demodulate the received data symbols, the channel estimation plays an important role to the system performance greatly. The most common technique to obtain channel information is via pilot aided channel estimation [2]. Pilot symbols consume both power and spectrum and thus it is desirable to keep the number of pilot symbols as minimum as possible. Some approaches for reduction of pilot overhead were proposed in [3-5]. On the other hand the spacing between pilot symbols should be small enough to make channel estimates reliable. Adaptive resource allocation in order to achieve a proper trade-off between utilized resources and quality of channel estimates based on CSI is necessary. Some authors discussed the number of used pilots in channel estimation and represent some methods for reduction them in OFDM systems. Authors in [6] use deviation of corresponding signals as a parameter to predict the channel characteristics in the transmitter end. They transmit fixed length of test signal to the channel whenever connection setup initiation takes place. Then by using the response, number of pilot signals to insert is determined and correspondingly appended to the data signal. Thus by varying the number of pilots depending upon the channel environment, it certainly improves the channel estimation and reduction in number of pilots used for channel estimation and feedback. The proposed estimator in [7] employs a specific pilot structure which consists of two types of pilot symbols with different pilot density. The combination of interference alleviation and pilot rearrangement not only makes the channel estimation robust to the time selectivity of the channel but also reduces the number of pilot subcarriers needed to estimate the channel. Authors in [8] develop a method to obtain the optimal number of known pilot symbols for pilot-aided linear channel estimation in OFDM. They derive an expression for channel estimation error covariance from which performance measures can be numerically evaluated to obtain the optimal number of pilot symbols. In [9], the shortest preamble that attains a given mean square error in a sequence that under-samples the channel spectrum is found. A high mobile wireless channel is time-variant due to Doppler frequency shift. Then, the number of used pilots in channel estimation depends on the Doppler frequency shift. So, we represent a lower bound for the number of pilots based on it. Also, the number of used pilots depends on the length of channel. Thus, we evaluate channel length estimation problem for obtaining another lower bound for the number of pilots. Finally the tight bound is obtained.
The reminder of this paper is structured as follows: in section 2 the system model is introduced. Bounds for number of used pilots in channel estimation are presented in section 3. Some simulation results are given in section 4 and finally section 5 concludes the paper.
2. OFDM System Model
The basic building block for OFDM transceiver is shown in Figure 1. In an OFDM transmitter, at the nth symbol time, K data symbols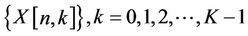 , are converted into time-domain signals using the inverse fast Fourier transform (FFT). A cyclic prefix (CP) is inserted to preserve the orthogonality between the subcarriers and to eliminate the interference between the adjacent OFDM symbols. At the receiver, the CP is removed before the FFT process. Assuming the ideal synchronization at the receiver, the received symbol of the k th subcarrier at the n th symbol time can be represented by:
, are converted into time-domain signals using the inverse fast Fourier transform (FFT). A cyclic prefix (CP) is inserted to preserve the orthogonality between the subcarriers and to eliminate the interference between the adjacent OFDM symbols. At the receiver, the CP is removed before the FFT process. Assuming the ideal synchronization at the receiver, the received symbol of the k th subcarrier at the n th symbol time can be represented by:
 (1)
(1)
where H[n,k] is the frequency response of the channel at the k th subcarrier and the n th symbol time, and Z[n,k] is the background noise, which can be approximated as zero-mean additive white Gaussian noise (AWGN) with variance 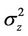 [10].
[10].
3. Bounds for the Number of Pilots
We study the number of used pilots for channel estimation in OFDM systems, and achieve the bounds for it. Here, we recall that unnecessary overhead is not desirable in terms of the resource allocation for the pilot signals. An appropriate pilot distribution is necessary using adaptive pilot allocation based on obtained bounds.
3.1. The First Lower Bound for the Number of Used Pilots in OFDM Systems
For proper channel estimation, it is necessary to sample channel according to the Nyquist theorem. The parameters of used in this section are listed in Table 1. Let us denote the spacing between pilot symbols in the time domain by  and in the frequency domain by
and in the frequency domain by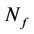 . The sampling theorem states that [11]:
. The sampling theorem states that [11]:
 (2)
(2)
where  and
and 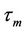 denote maximum Doppler frequency shift and maximum delay respectively.
denote maximum Doppler frequency shift and maximum delay respectively. 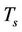 de-
de-

Figure 1. Baseband OFDM transceiver.
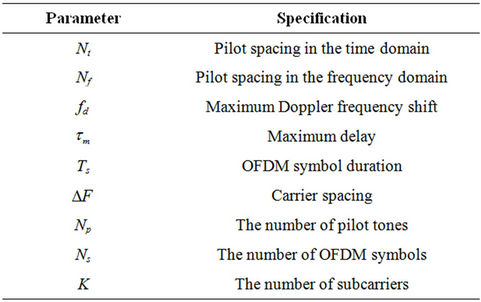
Table 1. The list of used parameters in section 3.1.
notes the OFDM symbol duration and the carrier spacing, 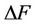 , is the spacing in the frequency domain. As illustrated in Figure 2, the transmitter sends pilot symbols scattered in the time and frequency domains in a regular pattern. Assuming that power spectrum density (PSD) of channel is based on jakes spectrum [12],
, is the spacing in the frequency domain. As illustrated in Figure 2, the transmitter sends pilot symbols scattered in the time and frequency domains in a regular pattern. Assuming that power spectrum density (PSD) of channel is based on jakes spectrum [12],  can be estimated as follows:
can be estimated as follows:
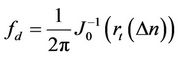 (3)
(3)
where  is the 0th order Bessel function of the first kind and
is the 0th order Bessel function of the first kind and 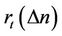 denotes the correlation function in the time domain. Also
denotes the correlation function in the time domain. Also 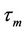 can be estimated with some approaches such as [13]. The
can be estimated with some approaches such as [13]. The 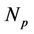 pilot tones are uniformly inserted into OFDM block.
pilot tones are uniformly inserted into OFDM block.  is calculated as follows:
is calculated as follows:
 (4)
(4)
where  is the number of OFDM symbols in the time domain.
is the number of OFDM symbols in the time domain.
Using Equations (2) and (4), the first lower bound for the number of used pilots is obtained as follows:
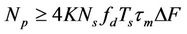 (5)
(5)
3.2. The Second Lower Bound for the Number of Used Pilots in OFDM Systems
We assume that channel impulse response is as follows:
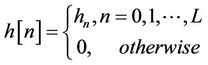 (6)
(6)
where L is the length of channel. Authors in [14] proposed an algorithm for estimation of the channel length without the need of pilots based on the second-order statistics of the received signal. Here, we represent a terse description of it.
Assuming an arbitrary positive integer N (N > L), we may construct an (N + 1) × 1 autocorrelation vector  for the received signal such that:
for the received signal such that:

Figure 2. Pilot symbols in the OFDM signals.
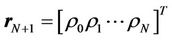 (7)
(7)
where
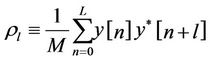 (8)
(8)
M denotes the sample size. Assume that the maximum lag N satisfies that N > L. A threshold 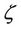 can be established as follows:
can be established as follows:
 (9)
(9)
where  is the parameter to be chosen and
is the parameter to be chosen and 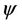 is denotes as the start-terminal-coefficients-to-channelgain ratio, which is related to the detectable start and terminal channel coefficients, such that:
is denotes as the start-terminal-coefficients-to-channelgain ratio, which is related to the detectable start and terminal channel coefficients, such that:
 (10)
(10)
The steps of proposed algorithm for channel length estimation in [14] are as follows:
Step 1: choose maximum lag N and sample size M. Set the threshold  according to Equation (9).
according to Equation (9).
Step 2: compute 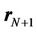 as given by Equation (7). Set
as given by Equation (7). Set .
.
Step 3: compute  with the threshold
with the threshold . Determine
. Determine  if
if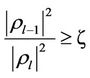 . Otherwise, decrement l by 1 and redo Step 3 until
. Otherwise, decrement l by 1 and redo Step 3 until .
.
Step 4: if , set
, set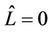 . where
. where 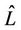 is estimated channel length.
is estimated channel length.
To control the detectability, 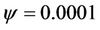 (high detectability) and
(high detectability) and 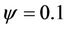 (low detectability) are chosen. The performance of presented channel length estimation method is not sensitive to the values of the parameter θ and is robust over all kinds of constellations such as BPSK and QPSK.
(low detectability) are chosen. The performance of presented channel length estimation method is not sensitive to the values of the parameter θ and is robust over all kinds of constellations such as BPSK and QPSK.
The following theorem states that, with knowing length of channel, we can have a bound for the number of pilots.
Theorem: assuming equi-spaced and equal power pilot tones with the number of pilot tones,  , greater than or equal to the channel length, implies:
, greater than or equal to the channel length, implies:
1) The covariance matrix of the channel estimation error , Σ, is a diagonal matrix.
2) If matrix Σ is diagonal, the MSEs of channel prediction are identical for all subcarriers.
3) Increasing the number of pilot tones greater than channel length will not enhance the performance of the channel predictor.
The proof of this theorem is given in [15]. Then, we have:
 (11)
(11)
3.3. Adaptive Algorithm for Pilot-Aided Channel Estimation Based on Tight Bound
We rename right hand of inequalities (5) and (11), as follows:
 (12)
(12)
Then
 (13)
(13)
Thus, we have a tight bound for the number of necessary pilots for channel estimation in OFDM systems as follows:
 (14)
(14)
The receiver, after calculating the tight bound for the number of pilots, feeds these values back to the OFDM transmitter such that these values will be used in the next transmission period. By exploiting CSI, The proposed system minimizes the pilot overhead while maintaining desired channel estimation accuracy. In other words, receiver by consideration the tight bound for the number of necessary pilots and environment conditions, decide that how many pilots should be used for channel estimation. Figure 3 illustrates proposed adaptive algorithm for pilot aided channel estimation in the OFDM systems.
4. Simulation Results
In this section, we evaluate the performance of proposed adaptive algorithm for channel estimation. Simulation parameters are shown in Table 2.
BER vs. SNR curves with  are shown in
are shown in
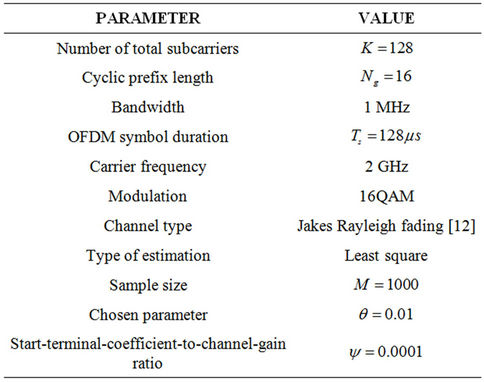
Table 2. Simulation parameters.

Figure 3. Proposed OFDM system with adaptive scheme for number of used pilots.

Figure 4. BER vs. SNR with L = 8, 12.
Figure 4. The adaptive pilot system based on the first lower bound is compared to fixed pilot system in Figures 5 and 6 in 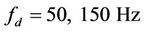 respectively.
respectively.
The fixed number of pilots is calculated according to the average situation of the environment and the number of adaptive pilots is equal to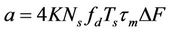 .
.
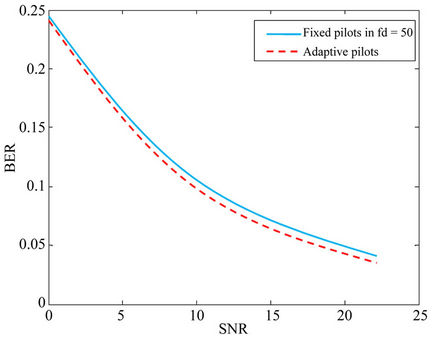
Figure 5. Performance improvement using adaptive resource allocation based on the first lower bound for the number of pilots,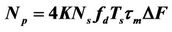 . Channel estimation using fixed pilots is implemented in fd = 50 Hz.
. Channel estimation using fixed pilots is implemented in fd = 50 Hz.

Figure 6. Performance improvement using adaptive resource allocation based on the first lower bound for the number of pilots, . Channel estimation using fixed pilots is implemented in fd = 150 Hz.
. Channel estimation using fixed pilots is implemented in fd = 150 Hz.

Figure 7. BER performance of the OFDM system with fixed pilots and adaptive pilots based on obtained tight bound with Np = B1 and Np = B2.
Figures 5 and 6 illustrate that adaptive pilot improves performance of OFDM system especially under high Doppler frequency shift. Figure 7 shows the bit error rate (BER) performance of the OFDM system with fixed pilots and adaptive pilots with 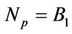 and
and . Proximity of curves for
. Proximity of curves for  and
and 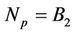 demonstrates that presented bound in section 3 is really tight.
demonstrates that presented bound in section 3 is really tight.
5. Conclusion
In this paper, we drive a new tight bound for the number of used pilots in channel estimation for OFDM systems. This bound is fed back to the transmitter adaptively to improve the system performance with low pilot overhead compared to the conventional schemes.
REFERENCES
- J. A. C. Bingham, “Multicarrier Modulation for Data Transmission: An Idea Whose Time Has Come,” Communications Magazine, Vol. 28, No. 5, 1990, pp. 5-14. doi:10.1109/35.54342
- O. Edfors, M. Sandell, J. J. Van de Beek, S. K. Wilson and P. O. Borjesson, “OFDM Channel Estimation by Singular Value Decomposition,” IEEE Transactions on Communications, Vol. 46, No. 7, 1998, pp. 931-939. doi:10.1109/26.701321
- G. Tauböck and F. Hlawatsch, “A Compressed Sensing Technique for OFDM Channel Estimation in Mobile Environments: Exploiting Channel Sparsity for Reducing Pilots,” IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, 31 March-4 April 2008, pp. 2885-2888.
- S. Bae, Y. Jang, S. Shin, Z. Chengshi and K. Kwak, “Two Dimentional Estimations with Reduced Pilot Arrangements for OFDM Systems,” Advanced Communication Technology International Conference, Phoenix Park, 15- 18 February 2009, pp. 503-506.
- M. Chang and T. D. Hsieh, “Detection of OFDM Signals in Fast-Varying Channels with Low-Density Pilot Symbols,” IEEE Transactions on Vehicular Technology, Vol. 57, No. 2, 2008, pp. 859-872. doi:10.1109/TVT.2007.906369
- J. Byng and N. P. Natarajan, “Adaptive Pilot Utilization for OFDM Channel Estimation in a Time Varying Channel,” IEEE 10th Annual Wireless and Microwave Technology Conference, Clearwater, 20-21 April 2009, pp. 1- 5.
- S. Lee, K. Kwak, J. Kim and D. Hong, “Channel Estimation Approach with Variable Pilot Density to Mitigate Interference over Time-Selective Cellular OFDM Systems,” IEEE Transaction on Wireless Communications, Vol. 7, No. 7, 2008, pp. 2694-2704.
- S. Ohno, E. Manasseh and M. Nakamoto, “How Many Known Symbols Are Required for Linear Channel Estimation in OFDM?” IEEE International Conference on Acoustics, Speech and Signal Processing, Prague, 22-27 May 2011, pp. 3580-3583.
- C. Oberli, M. C. Estela and M. Ríos, “On Using Transmission Overhead Efficiently for Channel Estimation in OFDM,” IEEE Transactions on Communications, Vol. 58, No. 2, 2010, p. 399. doi:10.1109/TCOMM.2010.02.070530
- J. W. Choi and Y. H. Lee, “Optimum Pilot Pattern for Channel Estimation in OFDM Systems,” IEEE Transactions on Communications, Vol. 4, No. 5, 2005, pp. 2083- 2088.
- P. Hoeher, S. Kaiser and P. Robertson, “Two-Dimensional Pilot-Symbol-Aided Channel Estimation by Wiener Filtering,” IEEE International Conference on Acoustics, Speech and Signal Processing, Munich, 21-24 April 1997, pp. 1845-1848.
- W. C. Jakes, “Microwave Mobile Communications,” Wiley, New York, 1974.
- S. A. Husen, S. Baggen and A. Filippi, “Blind Estimation of Maximum Delay Spread in OFDM Systems,” IEEE 64th Conference on Vehicular Technology, Montreal, 25- 28 September 2006, pp. 1-5.
- X. Wang, H. C. Wu, S. Y. Chang, Y. Wu and J. Y. Chouinard, “Analysis and Algorithm for Non-Pilot-Aided Channel Length Estimation in Wireless Communications,” IEEE Conference on Global Telecommunications, New Orleans, 30 November-4 December 2008, pp. 1-5.
- M. Karami, A. Olfat and N. C. Beaulieu, “Pilot Symbol Assisted Adaptive Modulation for OFDM Systems with Imperfect Channel State Information,” IEEE Conference on Global Telecommunications, Miami, 6-10 December 2010, pp. 1-6.
NOTES
*Corresponding author.

