Communications and Network
Vol.3 No.3(2011), Article ID:6898,16 pages DOI:10.4236/cn.2011.33021
Maximizing Resilient Throughput in Peer-to-Peer Network
1 School of Computer Science and Technology, Huazhong University of Science and Technology, Wuhan, China
2Department of Electrical Engineering and Computer Science at Vanderbilt University, Nashville, USA
3YouTube, LLC, San Francisco, USA
E-mail: bo.liu@hust.edu.cn, {fan.qiu, yanchuan.cao}vanderbilt.edu, binchang@google.com, {yi.cui, yuan.xue}Vanderbilt.edu
Received May 29, 2011; revised July 5, 2011; accepted July 12, 2011
Keywords: Peer-to-Peer, Resilient, Throughput, Maximizing
Abstract
A unique challenge in P2P network is that the peer dynamics (departure or failure) cause unavoidable disruption to the downstream peers. While many works have been dedicated to consider fault resilience in peer selection, little understanding is achieved regarding the solvability and solution complexity of this problem from the optimization perspective. To this end, we propose an optimization framework based on the generalized flow theory. Key concepts introduced by this framework include resilience factor, resilience index, and generalized throughput, which collectively model the peer resilience in a probabilistic measure. Under this framework, we divide the domain of optimal peer selection along several dimensions including network topology, overlay organization, and the definition of resilience factor and generalized flow. Within each subproblem, we focus on studying the problem complexity and finding optimal solutions. Simulation study is also performed to evaluate the effectiveness of our model and performance of the proposed algorithms.
1. Introduction
Peer-to-peer (P2P) has been proved a highly cost-effective content distribution solution, where peers self-organize themselves into an overlay network and relay data to each other, thus reducing server load. A central problem in the overlay network construction is peer selection, the strategy a peer employs to select other peer(s) as its parent(s) to receive data from. Peer selections aggregate into multicast tree(s) spanning from the server, the source of the data, to all peers. Given the data intensive nature of P2P applications (e.g., video streaming or bulk data distribution), a common objective is to maximize the data throughput to all peers.
Already challenging in its static setup, the optimal peer selection problem is further aggravated by the high Volatility of the P2P network. Due to various reasons such as user leaving or machine/network failure, unscheduled peer departure constantly happens, which results in service disruptions or outages on all the downstream peers. Therefore, we argue that when designing peer selection solutions, fault resilience deserves the same level of attention as first-class performance metrics, e.g. throughput, delay, etc.
A significant amount of research has been conducted on this topic with different emphasis. While important heuristics have been proposed such as minimizing depth [1,2], multiple trees [3,4], bandwidth-first, age-first [5], or a hybrid of the two [6], some analytical works have tried to analyze and compare their performances under stochastic framework [7,8] or real-system traces. However, this domain has been rarely examined from the optimization perspective. If we are able to model the fault-resilient peer selection problem under an optimization framework which combines fault resilience with key performance metrics such as throughput, standard optimization techniques can be practiced to evaluate key questions such as the solvability of the problem and the complexity of its optimal solutions, if any. Also existing heuristics could be quantitatively evaluated under the same framework.
In this paper, we report our initial research towards this direction. Our optimization framework is based on the generalized flow theory [9]. It generalizes the classical network flow problem by specifying a gain factor to each link in the network. As such, the objective is to optimize the throughput of the generalized flow as the product of raw flow and the gain factor on each link, while the traditional capacity and flow conservation constraints still apply to the raw flow. Widely employed in operation research to model the loss, theft, or interest rate in commodity transportation [10-12], we find it a good match to the P2P domain. If we assign each peer a resilience factor as the probabilistic measure of its chance of survival within a given time horizon, this resilience factor could be considered as the gain factor in the generalized flow setting. Under this framework, the problem of fault resilient peer selection becomes to maximize the aggregation of generalized flow received by each peer, which is the product of the raw flow and resilience factors of peers it passes along.
We study this problem under a multitude of problem settings. Specifically• Regarding network model, we consider two types of topologies: the general topology which models the underlying physical network as a graph, and the star topology which assumes the bottleneck does not exist in the physical network, but on only on peer’s access link.
• Regarding overlay organization, we consider cases where the number of trees interconnecting peers is unlimited or upper-bounded, e.g., single tree.
• Along the dimension of generalized flow definition, we consider concatenation model where the generalized flow delivered to a peer depends on the resilience of all its ancestors, and non-concatenation model which only considers the resilience of its immediate parent.
Along these dimensions, we explore the entire spectrum of this domain, and focus on studying problem complexity and finding the optimal solutions within each subproblem.
The rest of this paper is organized as follows. In Sec. 2, we introduce our optimization framework and formally define key concepts such as generalized flow and resilience index. In Sec. 3, we study the optimal peer selection problem under the general topology, and propose two algorithms employing linear programming techniques. In Sec. 4, we study the same problem under the star topology, and propose two algorithms based on combinatorial optimization techniques. Sec. 5 presents evaluation results. Finally, we discuss related works in Sec. 6 and conclude in Sec. 7.
2. Framework Overview
2.1. Network Model
We consider two kinds of network models: star model and general model.
2.2.1. General Network
We model the network as a graph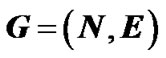 , with capacity ce on each physical edge
, with capacity ce on each physical edge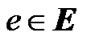 . On top of G, an overlay network
. On top of G, an overlay network 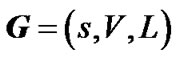 exists, where s is the server, and peers belong to the set
exists, where s is the server, and peers belong to the set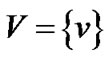 . Each overlay edge
. Each overlay edge 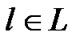 connects two peers in V, and corresponds to the uni-cast route at the physical network G.
connects two peers in V, and corresponds to the uni-cast route at the physical network G.
2.2.2. Star Network
Many works [13] have implicitly assumed that the bottleneck of a uni-cast path only happens at either access link of its two end hosts. In this way, we can simplify the general model into a star model. The central node of the star represents the Internet cloud, which reaches out to every peer. In this model, we denote the outbound bandwidth of peer 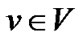 as cv.
as cv.
2.2. Overlay Organization
To transfer data among peers, the simplest and most straight forward strategy is a single multicast tree spanning from the server s to all peers in V. Although simple to manage, this solution has clear drawback since a peer departure can cause complete disruption to all its descendants.
An alternative solution is the recently popular multitree or mesh solution, where each peer schedules to receive data from multiple parents. Since the mesh structure can be usually decomposed as the sum of multiple spanning trees, therefore will be categorized as multi-tree solution1. We denote the tree set as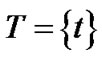 , where each tree
, where each tree 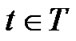 covers all peers and has a single rate f(t).
covers all peers and has a single rate f(t).
2.3. Resilience Factor and Generalized Flow
We assign a resilience factor 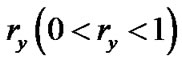 to each peer
to each peer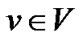 . Our model makes no assumption on how
. Our model makes no assumption on how 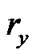 is defined. For the purpose of illustration, we introduce one way to define
is defined. For the purpose of illustration, we introduce one way to define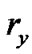 . Suppose v follows certain lifetime distribution with c.d.f. F(τ), and T is a random variable denoting the time of departure, then the survival function of v is
. Suppose v follows certain lifetime distribution with c.d.f. F(τ), and T is a random variable denoting the time of departure, then the survival function of v is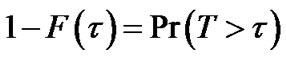 , the probability that its time of departure is later than time τ. If we denote
, the probability that its time of departure is later than time τ. If we denote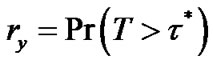 , where τ∗ is a fixed time point in the future, then it represents the chance of survival for v until τ∗.
, where τ∗ is a fixed time point in the future, then it represents the chance of survival for v until τ∗.
Given the resilience factor of v, we consider two models to compute the rate of generalized flow.
2.3.1. Concatenation Model
For each peer v in tree t, there is a path from the server s to v, denoted as:
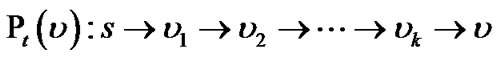
Given t’s flow rate f(t), the dependency model computes the generalized flow delivered to v as f(t) timed by the concatenate product of rv1 through rvk. We define such product as the resilience index of v in t:
 (1)
(1)
Based on this definition, f(t)Rt (v) is the generalized flow rate delivered to v in tree t. We can further define the resilience index of tree t as:
 (2)
(2)
Since Rt(v) ≤ 1, it is obvious that R(t) ≤|V|. Now we are able to define generalized throughput of t, which is the sum of generalized flow rates to all peers.
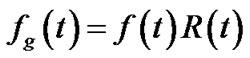 (3)
(3)
This model computes a peer’s generalized flow by factoring in the resilience factors of all its ancestors. It fits the live P2P streaming scenario where a peer failure can cause disruptions on all its descendants. Also an implicit assumption in the definition of Rt(v) is that the resilience factor of server s is 1, i.e., s will not departure.
2.3.2. Non-concatenation Model
In this model, we define the generalized flow to a peer to be only dependent on its immediate parent. Formally, in the same sample context of concatenation model, we define the resilience index of peer v in tree t as follows.
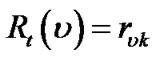 (4)
(4)
This model fits better to P2P applications with no real time constraints. For example, in some on-demand streaming and downloading applications, the parent peer serves its children from its local cache. This gives its children buffering time to find new parent(s) upon its own departure or failure, thus absorbing the impact of cascading disruption.
Finally, in Table 1, we summarize findings when exploring along the three dimensions outlined in this section. Of the eight sub-problems, we find four of them polynomially solvable and present the optimal solutions. Of the four NP-hard problems, we are able to find a O(logε)-approximation algorithm, and only find heuristics to the other three. We also summarize notations appeared in this paper in Table 2.
3. General Topology Model
In this section, we present our study on optimal generalized throughput under the general topology model, as shown in Figure 1.
3.1. Multiple Tress
We start with the most basic setting, where an unlimited number of trees can be constructed for the purpose of maximizing generalized throughput. With notions introduced in Sec. 2, we formulate it into the following linear programming (LP) problem.
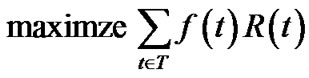 (5)
(5)
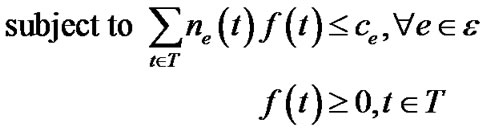 (6)
(6)
The objective of problem (5) is to maximize the generalized throughput (defined in Equation (3)) of all trees. Inequality (6) refers to the capacity constraint, i.e., the aggregate raw flow of all trees cannot exceed any physical link e∈E. ne(t) is an integer variable indicating the number of times tree t has passed through e. Note since t is an overlay tree, ne(t) can be greater than 1.
The central difficulty of problem (5) is that its number of variables is exponential to the size of the P2P network. Based on Cayley’s theorem [14], the number of different spanning trees contained in T is |T|= (|V|+ 1)(|V|−1), |V| being the number of peers in V.
On the other hand, the dimensionality of this problem, i.e., the number of constraints, is |E|, the number of physical links. This gives us a chance to solve this problem via its dual presented as follows, which contains |T| variables but exponential constraints.

Table 1. Summary of findings.
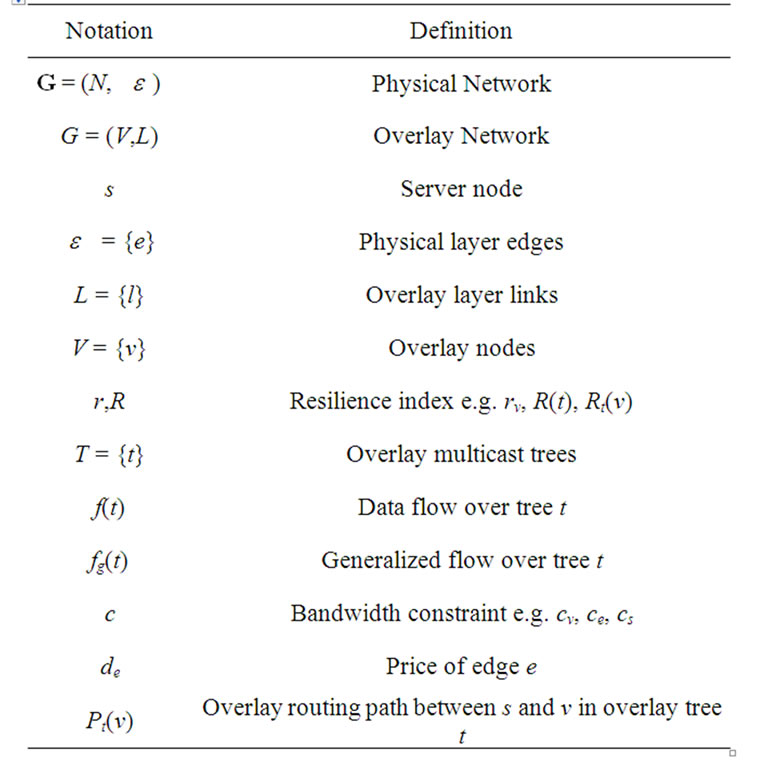
Table 2. Notations table.
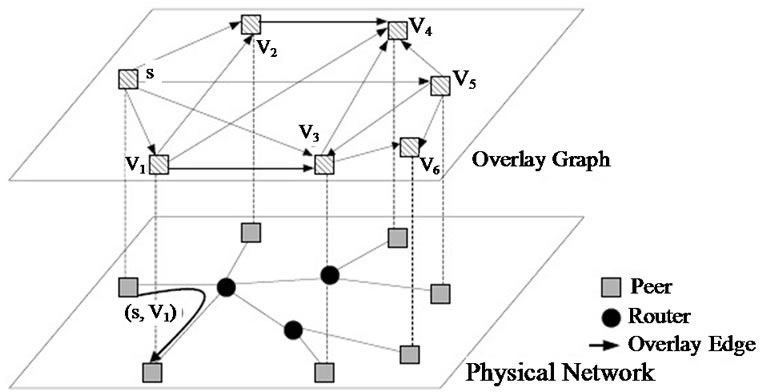
Figure 1. General topology model.
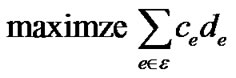 (7)
(7)
 (8)
(8)
Problem (7) refers to assigning each link e a length de, and minimize the sum of de multiplied by the capacity ce, subject to inequality (8), which states that the length of any spanning tree must be greater than its own resilience index R(t), defined in Equation (2).
Although there exists exponential number of trees in T, if we can find a separation oracle able to check whether constraint (8) is met in polynomial time, then the dual problem (7) is solvable in polynomial time, hence the primal problem.
To find if such an oracle exists, we first adapt the definition of R(t) from peer-based to link-based, to be consistent with the left side of constraint (8). This can be easily achieved as follows. We assign a resilience factor re to each link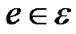 , and define it as:
, and define it as:
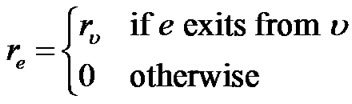 (9)
(9)
As articulated in Sec. 2.3, we have different definitions on R(t) for concatenation and non-concatenation models. We start with the non-concatenation model first.
Based on the definition on resilience index Rt(v) shown in Equation (4), we can easily observe that R(t) in this case is the sum of resilience factors of all non-leaf peers in tree t. Translated into the link-based definition, it is the sum of resilience factors of all links in t, i.e., R(t) = Σe∈t ne(t)re. This allows us to reformulate Inequality (8) into the following.
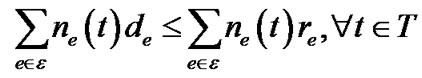
It is now clear that the separation oracle is a minimum spanning tree algorithm that sees the cost on each link e as (de − re). Constraint (8) will be satisfied if the cost of the found minimum spanning tree is still greater than 0.
To this end, we present a fully polynomial time approximation scheme (FPTAS). FPTAS is a family of algorithms which finds a 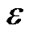 -approximate solution returning a result at least (1 −
-approximate solution returning a result at least (1 −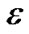 ) times the maximum value, for arbitrary error parameter
) times the maximum value, for arbitrary error parameter  > 0.
> 0.
Table 3 shows the MultiTrees-General algorithm. It solves the primal and dual problems in an iterative fashion. It sets initial length to β all links in E. In each iteration, it finds the minimum spanning tree t∗ based on the cost (de − re), and route traffic over t∗. Based on the traffic increment, the length de is updated as defined in line 10. Finally, the algorithm terminates when constraint (8) is satisfied, i.e., when the cost of the minimum spanning tree is greater than 0. Note that since the aggregated raw flow of all returned trees can exceed the capacity of certain physical links, we introduce the index le to record the congestion ratio on each link e. By scaling the rate of each tree with the maximum congestion noted by lmax, the algorithm is guaranteed to return a feasible solution. We summarize the property of this algorithm in Theorem 1.
Theorem 1: Under the non-concatenation model, when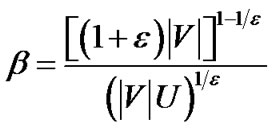 , the MultiTrees-General algorithm returns the solution at least (1 − 2
, the MultiTrees-General algorithm returns the solution at least (1 − 2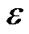 ) times the optimal result of problem (5), with running time
) times the optimal result of problem (5), with running time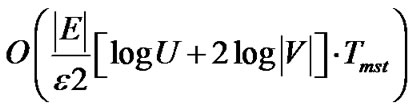 . U is the length of the longest uni-cast route and Tmst is the running time of the minimum spanning tree algorithm.
. U is the length of the longest uni-cast route and Tmst is the running time of the minimum spanning tree algorithm.

Table 3. Finding multiple trees under general topology model.
Now we turn to the concatenation model, where the resilience index is defined in Equation (1). In this case, each peer’s resilience index is the product of resilience factors of all its ancestors. Although we can perform logarithm operation on resilience factors re and solve this problem using Dijkstra’s algorithm, it becomes extremely hard when combining with length assignment de, which needs to be solved by a minimum spanning tree algorithm. In the following theorem, we prove this problem to be NP-hard, by reducing its separation oracle to the problem of 3-SAT.
Theorem 2: Under the concatenation model, the MultiTrees-General problem (5) is NP-hard.
3.2. Single Tree
A salient feature of the MultiTrees-General algorithm is that it reveals the maximum generalized throughput a P2P network can achieve. However, given the exponential selection space in tree set T, the algorithm often returns a high number of trees, which are hardly manageable in practice. For practical purposes, we enforce a limit on the number of trees we can construct. To achieve so, we modify problem (5) into the following integer programming problem.
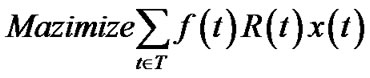 (10)
(10)
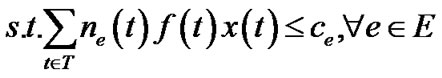 (11)
(11)
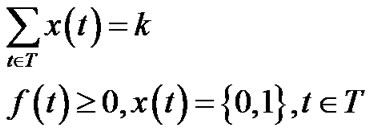 (12)
(12)
Problem (10) introduces a 0 - 1 variable x(t), and k, the upper limit on the number of trees. This constraint is enforced by Equation (12). This problem is NP-hard since its special case has been proved so. When k = 1 and resilience factor of all peers are 1, this problem reduces to maximizing the throughput of a single overlay multicast tree, which was shown NP-hard in [15] under the name MPSP (Multicast Path Set Problem).
Following the same idea of the MultiTrees-General algorithm, we assign length to each physical link to find minimum spanning tree, but only in an online fashion. The algorithm runs k iterations, in each of which a tree is returned. The details of the algorithm can be found in Table 4.
We note that the two algorithms presented in this section can be also applied to the concatenation model. However, theorem 1 will not apply due to the NP-hardness of separation oracle for problem (5).
4. STAR Topology Model
The algorithms presented in Sec. 3 rely on linear programming technique, and operate on both overlay network L and physical network whose measurement can be expensive. They require complete knowledge on the physical network, i.e., the capacity of any physical link e ε, if it appears in the underlying routing path that connects any overlay link l
ε, if it appears in the underlying routing path that connects any overlay link l L.
L.
Many P2P research works have chosen to rely on a simplified assumption, which imposes outgoing bandwidth

Table 4. Finding k trees under general topology model.
constraint on each peer and allow it to parent other peers until its outbound bandwidth depletes. In other words, the Internet cloud is assumed to have enough capacity supporting all peers. This effectively transforms the physical networkεinto a star network, whose central hub represents the Internet cloud reaching out to all peers, as shown in Figure 2. In this section, we study the same set of problems under such a special topology.
4.1. Multiple Trees
We again start with the case of multiple trees. To simplify the illustration, we remove notations associated with the general network ε. Instead, we introduce notations cv to denote outbound bandwidth of peer v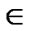 V, cs to denote outbound bandwidth of the server s, and nv(t) or ns(t) to denote the number of children v or s have in tree t. The problem formulation is as follow s2.
V, cs to denote outbound bandwidth of the server s, and nv(t) or ns(t) to denote the number of children v or s have in tree t. The problem formulation is as follow s2.
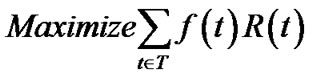 (13)
(13)
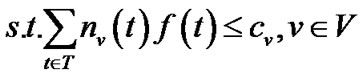 (14)
(14)
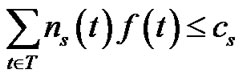 (15)
(15)
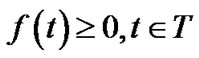 (16)
(16)
Inequalities (14) and (15) refer to the capacity constraint. In fact, problem (13) is only a special case of the problem (5), thus can be solved by algorithm MultiTrees-General in the same linear programming fashion. However, given the simplified topology, we are interested to find out if this problem can be simply addressed through combinatorial optimization techniques.
Table 5 shows the MultiTrees-Star algorithm. It construct at most |V| + 1 trees in the order shown in Figure 3.
Starting from peer v1 with the maximum resilience factor, tree t1 is constructed, which depletes the outbound bandwidth of v1. The process continues until v|V| or the server bandwidth cs runs out. If there is still residue of cs after tree t|V| is finished, we construct a special tree t0 to deplete cs. We show the optimality of this simple algorithm as follows.
Theorem 3: MultiTrees-Star algorithm returns the optimal result of problem (13).
It is easy to observe that this theorem applies to both non-concatenation and concatenation models, since trees t0 through tn return the same resilience index under either definition, i.e., Equation (1) for concatenation model and
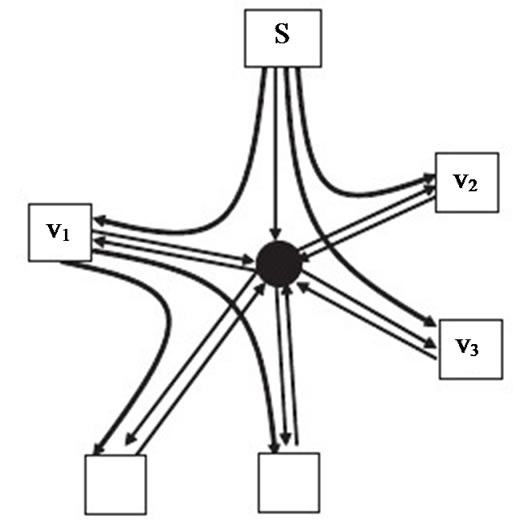
Figure 2. Star topology model.

Table 5. Finding multiple trees under star topology model.
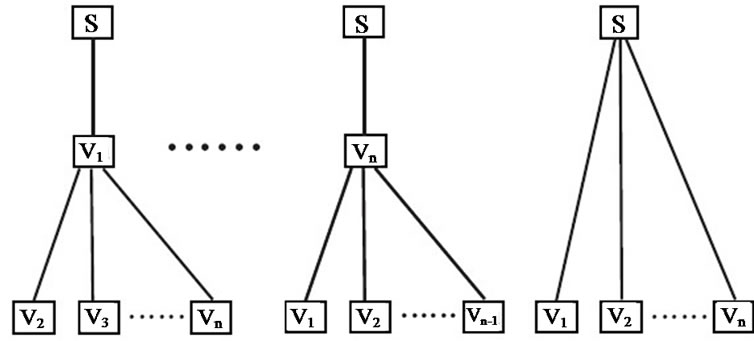
Figure 3. Lllustration of MulTitrees-Star algorithm.
Equation (4) for non-concatenation model.
The trees found by the MultiTrees-Star algorithm comply with many heuristics practiced by existing works. In terms of tree structure, t0 through tn are “fat trees” or “minimum-depth tree”. In terms of construction order, the algorithm starts from the peer with maximum resilience factor, which suggests maximum lifetime. This complies with the “longest-first” approach that assigns higher priority to peers with longer expected lifetime.
4.2. Single Tree
The number of trees returned by the MultiTrees-Star algorithm scales up linearly with |V|, the size of the P2P network. Although more scalable than the MultiTreesGeneral algorithm, the number of trees can be still too big as the P2P network grows.
To limit the number of trees, we can impose an additional integer constraint over problem (13) in the same fashion we defined problem (10) under the general topology model.
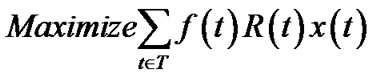 (17)
(17)
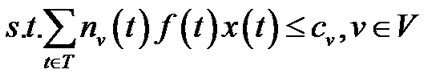 (18)
(18)
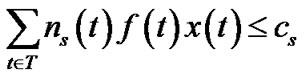 (19)
(19)
 (20)
(20)
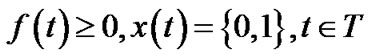 (21)
(21)
In particular, we are interested in the case when k = 1, i.e., when only one tree is allowed.
We start with the non-concatenation model. Table 6 shows the SingleTree-Star algorithm, which further contains two sub-algorithms. MaxRate-Star finds out the maximum rate a single tree can possibly afford. It works in a trial-and-error fashion by proposing a rate f and learning the maximum outbound degree the server s and each peer in V can support based on f. Starting from the server outbound bandwidth cs, f keeps shrinking until the sum of outbound degrees exceeds or equals to |V|, the number of peers. MostResilientTree-Star is a greedy algorithm constructing the tree with the highest resilience index. Given rate f, it gives priority to peers with the highest resilience factor and assign children to them up to their maximum outbound degrees. The algorithm returns the generalized throughput, which according to the definition in Equation (3), is the product of f and the returned tree’s resilient index.
With these two sub-algorithms, The SingleTree-Star algorithm finds the optimal tree by feeding different rates to MostResilientTree-Star and keeping track the tree returning the maximum generalized throughput. The trial starts from the maximum affordable rate found by MaxRate-Star, and ends when the outbound degree of the server s becomes |V|. In this case, we can construct tree t0 shown in Figure 3, which has the maximum resilience index |V|. Since in each iteration of SingleTree-Star, at least one peer’s outbound degree will in



Table 6. Finding single tree under star topology.
crease by 1, the number of iterations is bounded by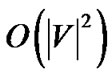 . Combined with the linear running time of MostResilientTree-Star, its overall running time is
. Combined with the linear running time of MostResilientTree-Star, its overall running time is . The following theorem establishes the optimality of SingleTree-Star.
. The following theorem establishes the optimality of SingleTree-Star.
Theorem 4: Under the non-concatenation model, the SingleTree-Star algorithm returns the optimal solution for problem (17) when k = 1, with running time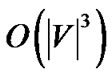 .
.
When applying the same algorithm to concatenation case, we find that the greedy approach of MostResilientTree-Star does not fit the multiplicative definition of resilience factor given in Equation (1). Essentially, although finding the tree with the maximum resilience index is solvable by a multiplicative-variant of Dijkstra’s algorithm, it becomes hard when imposing degree constraints on the peers. To show NP-hardness of this problem, we consider its special case, the maximum multiplicative cost path problem (MMCP), then reduce it to the Hamiltonian path problem.
Evidently, under the concatenation model, the intrinsic conflict between outbound bandwidth and resilience factor poses great barrier to our effort to assign priority in peer selection. On the other hand, the problem becomes polynomially solvable under the same framework of SingleTree-Star if all peers are identical over either of above metrics. For example, if all peers have the same resilience index, we only need to modify MostResilientTree-Star to greedily choose peers with the highest outbound bandwidth. If all peers have the same outbound bandwidth, the exact algorithm in Table 6 can be reused with no modification.
We note that algorithms listed in this section have assumed the inbound bandwidth of all peers are unlimited. Nevertheless, they can be easily modified when applying this constraint. Since our paper studies single-rate multicast, i.e., the rate of raw flow delivered to each peer is the same, we only consider cin, the minimum inbound bandwidth of all peers. If cin ≥ cs, then one should not be concerned since the raw flow delivered to a peer cannot exceed the outbound bandwidth of the server s. Otherwise, cin replaces cs as the bottleneck. As such, we only need to replace cs with min{cs, cin} in Tables 5 and 6.
4.3. Discussions
We finally discuss the implement-ability of algorithms presented in this paper. Given the unlimited number of trees the MultiTrees-General algorithm can produce, its main purpose remains to provide the theoretical optimal point against which other practical solutions can be measured. The k-Tree algorithm in Table 4 avoids this pitfall by limiting the number of trees. However, its functioning requires measurement overhead of the underlying physical network. The MultiTrees-Star and SingleTree-Star algorithms address both of the above issues. However, a centralized entity, e.g., the server s, needs to be in place. It collects uplink bandwidth information and resilience factors from all peers, then runs the algorithm. While it is reasonable to expect the server to keep the up-to-date information of the peers it serves, the distributed versions of these algorithms, if possible, are often desirable and constitutes the future direction of our research.
5. Evaluations
In this section, we present our evaluation study, which mainly carries two purposes. First, we will evaluate the validity of the generalized flow optimization framework at capturing the key characteristics of fault resilient peer selection problem. Second, we will study the performance of the algorithms proposed in this paper, as well as several well-known heuristics, at maximizing the generalized throughput and maintaining fairness.
5.1. Experimental Setup
We use simulation to evaluate the performance of our algorithm. Two experimental topologies are chosen. The first one is a 1000-node router-level network (2000 edges) created by the Boston BRITE topology generator using the Waxman model. Any pair of routers are connected by a pair of links with opposite directions. The bandwidth of physical links between routers, as well as peers’ access links, are normally distributed from 100 Kbps to 1000 Kbps. The second topology follows the star configuration outlined in Figure 2.
Under both topologies, we create 100 peers with unlimited inbound bandwidth. Under the general topology, they are randomly attached to the routers in the network.
Each simulation run lasts a finite time period. Starting from time 0, each peer is assigned a lifetime based on exponential and Pareto lifetime distributions with mean lifetime varying from 1500 seconds to 3500 seconds. The simulation run expires when the lifetime of the longest-lived peer expires. In our simulation, we assign resilience factor to each peer based on its expected lifetime in each particular run. Our algorithms are executed at the beginning of each run, taking the resilience factors and outbound bandwidths of all peers as the input, and returning single or multiple trees whose combined generalized throughput is maximized.
As time proceeds, peers expire one by one, which gradually tears down the tree(s) constructed at the beginning of the simulation. To capture this effect, we accumulatively calculate the amount of data collected by each peer until its ancestor or itself fails. We term this result as Volume, which represents the capability of the constructed tree(s) at collecting data for all peers before they demise.
5.2. Generalized Throughput vs. Volume
The objective of our algorithms is to maximize the generalized throughput, given resilience factors of all peers. However, it merely represents the expected amount of data the constructed tree(s) can possibly collect. Therefore, to test the fitness of our model under simulated P2P network with peer dynamics, we need the metric Volume, which counts the total amount of data collected. If our experiment can establish a proportional relationship between generalized throughput and Volume, then we can claim with high confidence level that our optimization framework can effectively model the dynamics of P2P network, and the developed optimization algorithms are able to increase the resilient throughput under such dynamics. Based on this consideration, our simulation does not include repairing mechanisms, i.e., a peer is not allowed to reconnect to the P2P network once disconnected due to the departure of either its ancestor or itself. This way, the recorded Volume can more accurately reflect the resilience of the tree(s) constructed by our algorithm.
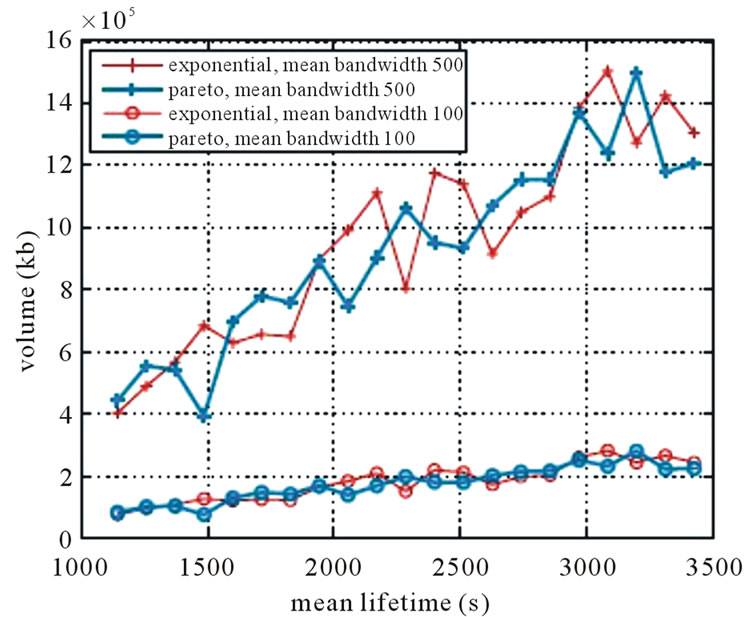
In Figure 4, we run the MultiTrees-General algorithm under the general topology, and contrast the generalized throughput returned by the algorithm in (a), calculated Volume in (b). We observe that the performance difference under two lifetime distributions are consistently obeyed in both figures when varying the mean peer lifetime.
We then run the MultiTrees-Star under the star topology, and contrast the generalized throughput and Volume by varying the mean outbound bandwidth. We further introduce two heuristic single-tree algorithms. In both heuristics, we compute the mean outbound bandwidth, and the mean resilience factors of all peers, then assign rate of the tree as the ratio of the two. Heuristic A constructs the tree by assigning priorities to peers with higher resilience factors, and heuristic B assigns priorities to the ones with higher outbound bandwidth. Our purpose is simple: if algorithms not developed under our optimization framework can still establish proportional relationship between generalized throughput and Volume, then it becomes more convincing that the generalized flow model can effectively capture the dynamic characteristics of P2P network. As shown in Figure 5, performance ordering of these algorithms under different
 (a)
(a) (b)
(b)
Figure 4. Performance of multitrees-General under nonconcatenation model. (a) Volume; (b) generalized throughput.
lifetime distributions are consistent in both figures.
5.3. Performance of Single Tree Algorithms
To evaluate the ability of single tree algorithms at maximizing the generalized throughput, we run heuristics A and B, and SingleTree-Star algorithm under the star topology and concatenation model, and normalize their results with the one achieved by the optimal MultiTree-Star algorithm. In Figure 6, we observe that all of them are able to maintain the performance ratio from 0.1 to 0.6 under different mean outbound bandwidths, mean lifetime, and lifetime distributions.
In Figure 7, 8, and 9, we display the sorted per-node generalized throughput and Volume for MultiTrees-Star, SingleTree-Star, and the two heuristics.
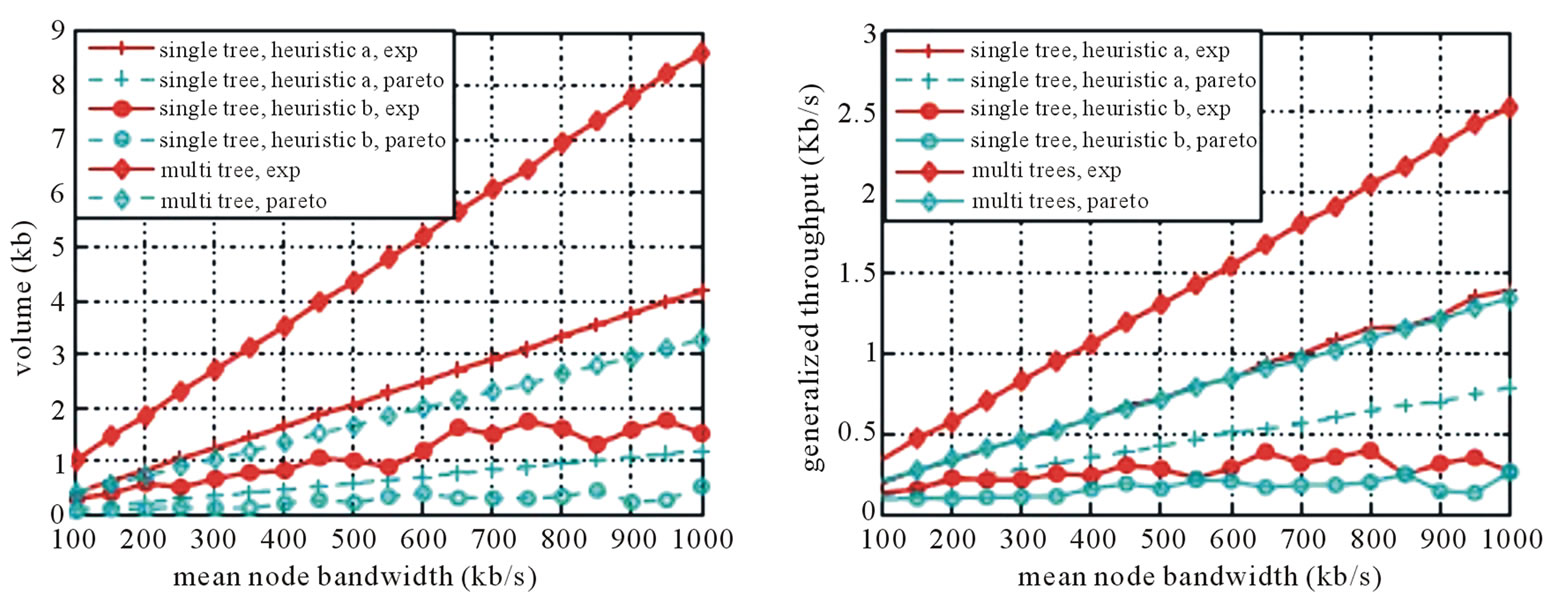
Figure 5. Performances of MultiTrees-Star and two heuristics under concaternation model (mean lifetime = 1500 s). (a) Volume; (b) generalized throughput.

Figure 6. Performances radio of heuristics to MultiTrees-Star under concaternation model. (a) Outbound bandwidth; (b) lifetime.
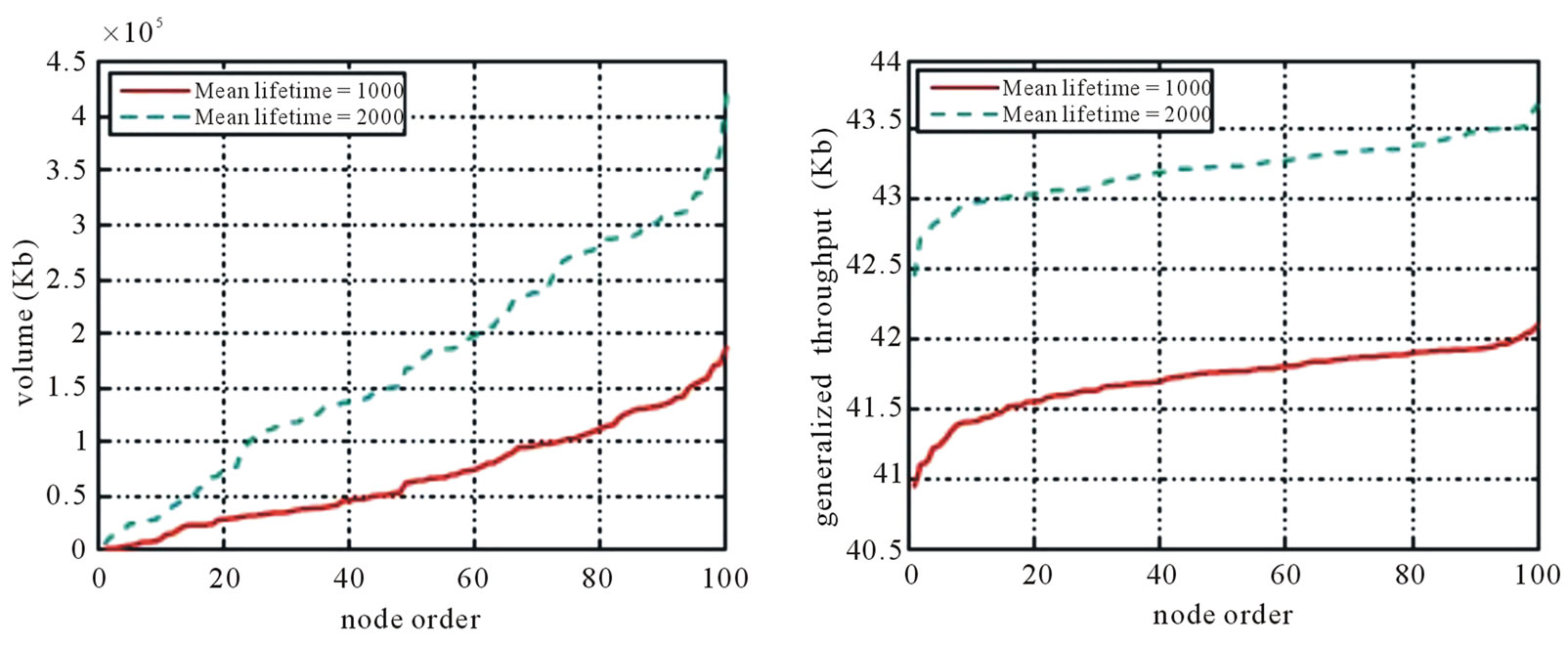
Figure 7. Sorted nodes of MultiTrees-Stae (mean outbound bangwidth = 100 Kbps). (a) Volume; (b) Generalized throughput.
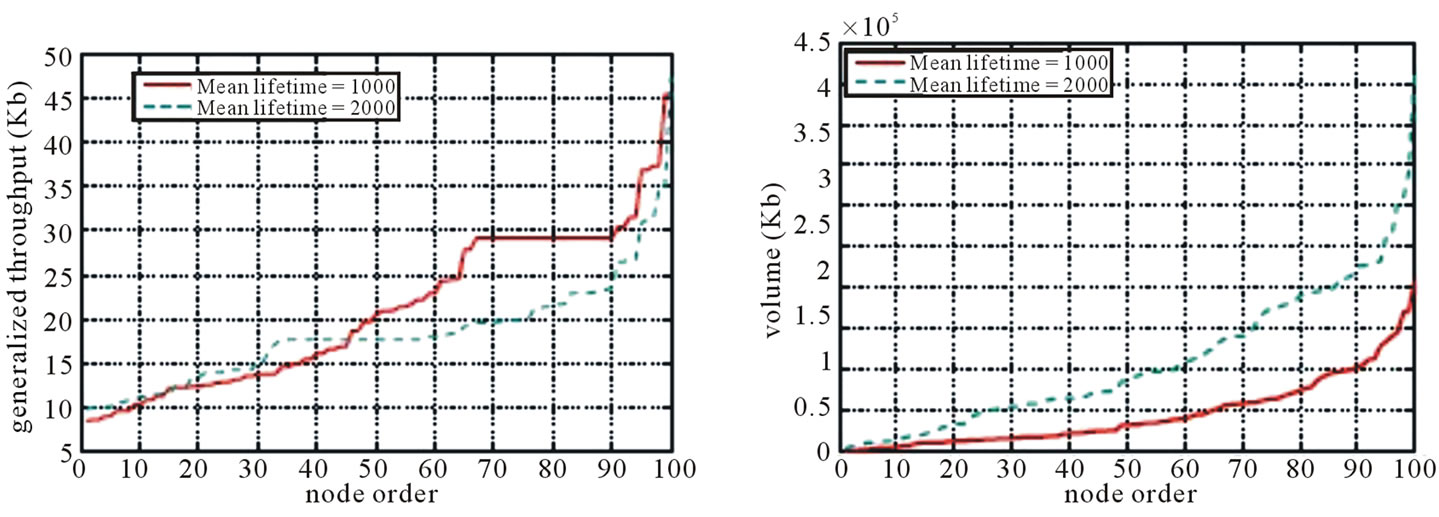
Figure 8. Sorted nodes of singletree-Star under non-concatenation model (mean outbound bandwidth = 100 Kbps). (a) Volume; (b) Generalized throughput.

Figure 9. Sorted nodes of heuristics under concatenation model (mean outbound bandwidth = 100 Kbps). (a) Volume; (b) Generalized throughput.
6. Related Work
Fault resilience has been considered in many existing solutions in overlay and P2P networks. An important approach is to reduce the tree depth to minimize failure propagation and service delay. Algorithms bearing the flavor of “minimizing depth” have been proposed in [1], [2], etc. Several well-known works, such as Bullet [16], SplitStream [3], and CoopNet [4], also employs the multi-tree approach to reduce the impact of peer failure, meanwhile increasing the aggregate throughput. In contrast to the depth-optimizing approach, Sripanidkulchai et al. [5] propose the longest-first algorithm which, by utilizing peers’ heavy tailed lifetime distribution, grants the longest lived peer with higher priority. These algorithms coincide with many findings in our paper, such as the optimal tree structure exhibited in the multi-tree setting under star network model.
Several evaluative works have been conducted to study the impact of different overlay construction algorithms on the resilience of P2P network. Bishop et al. examines the effect of bandwidthand age-priority heuristics on multicast tree reliability using trace-based simulation [6]. Stochastic network analysis have been employed to study the resilience of DHT based P2P network [7] and decentralized P2P network [8] under given peer lifetime distribution. In contrast, our work does not make a priori assumptions on peer characteristics, but focuses on finding optimal peer selection algorithms that can take any input.
Optimization has long been practiced in network routing, primarily based on the multi-commodity flow theory. The basic idea is to assign weights to links to reflect their congestion conditions, and perform traffic routing based on the weights. In particular, the work of [17,18] presents the theoretical models for online unicast routing. In the multicast domain, the work of [19] investigate the case of receivers within a multicast session arriving in batch, and the work in [20] presents a solution for receivers arriving separately. In the past, we have extended the multi-commodity flow theory to maximize the throughput of overlay multicasting [21]. This work is our initial effort to further incorporate fault resilience by introducing generalized flow theory.
Generalized flow has many applications [9], where the gain factors can model physical transformations of a commodity due to leakage, evaporation, breeding, theft, also transformations from one commodity into another as a result of manufacturing, scheduling, or currency exchange, etc. Exiting works have been focused on unicast routing [10,11]. In particular, Wayne et al. [12] present a Dijkstra-variant shortest path algorithm for minimumcost unicast-based generalized flow problem if all gain factors are below one. It is our finding in this paper that when applying to multicasting, the difficulty of the problem increases rapidly due to the complexity brought up by the exponential cardinality of multicast tree set.
7. Conclusions
In this paper, we propose an optimization framework based on the generalized flow theory. Utilizing the concept of gain factor in this theory, we introduce the resilience factor of peer to model its chance of survival in a probabilistic measure, and propose an optimization framework targeting at maximizing generalized throughput as the product of raw throughput and resilience factors. We report our findings in this problem domain along several dimensions including network topology, overlay organization, and concatenation model.
Our future work will carry along two directions. On the theoretical front, we will study whether improvement space exists for optimal algorithms presented in this paper, such as SingleTree-Star. On the practical front, we will design the lightweight distributed solution of our algorithms, especially under the star topology model. We are also interested to search for simple heuristics and have quantitatively evaluated within our optimization framework.
8. Acknowledgements
This work was supported by NSF award 0643488, Vanderbilt Discovery grant, and a gift from Microsoft Research.
9. References
[1] M. Guo and M. Ammar, “Scalable Livideo Streaming to Cooperative Clients Using Time Shifting and Video Patching,” Proceedings of the International Conference on Computer Communications and Networks, Chicago, 11-13 October 2004.
[2] V. Padmanabhan, H. Wang and P. Chou, “Resilient Peer-to-peer Streaming,” 11th IEEE International Conference on Networking Protocols, Atlanta, 4-7 November 2003, pp. 16-27. doi:10.1109/ICNP.2003.1249753
[3] M. Castro, P. Druschel, A. M. Kermarrec, A. Nandi, A. Rowstron and A. Singh, “Splitstream: High-Band Width Multicast in Cooperative Environments,” Proceedings of the Nineteenth ACM Symposium on Operating Systems Principles, Vol. 37, No. 5, 2003, pp. 298-313. doi:10.1145/945445.945474
[4] V. N. Padmanabhan, H. J. Wang, P. A. Chou and K. Sripanidkulchai, “Distributing Streaming Media Content Using Cooperative Networking,” Proceedings of the 12th International Workshop on Network and Operating Systems Support for Digital Audio And Video, New York, 2002, pp. 177-186. doi:10.1145/507670.507695
[5] K. Sripanidkulchai, A. Ganjam, B. Maggs and H. Zhang, “The Feasibility of Supporting Large-Scale Live Streaming Applications with Dynamic Application End-Points,” ACM SIGCOMM Computer Communication Review, Vol. 34, No. 4, 2004, pp. 107-120. doi:10.1145/1030194.1015480
[6] M. Bishop, S. Rao and K. Sripanidkulchai, “Considering Priority in Overlay Multicast Protocols under Heterogeneous Environments,” Proceedings of 25th IEEE International Conference on Computer Communications, Barcelona, April 2006, pp. 1-13. doi:10.1109/INFOCOM.2006.140
[7] G. Tan and S. Jarvis, “On the Reliability of DHT-Based Multicast,” Proceeding of International Conference on, Computer Communications and Networks, Honolulu, 13- 16 August 2007.
[8] D. Leonard, Z. Yao, V. Rai and D. Loguinov, “On Lifetime-Based Node Failure and Stochastic Resilience of Decentralized Peer-to-peer Networks,” IEEE/ACM Transactions on Networking, Vol. 15, No. 3, 2007, pp. 644-656.
[9] R. Ahuja, T. Magnanti and J. Orlin, “Network Flows: Theory, Algorithms, and Applications,” Englewood Cliffss, Bergen, 1993.
[10] K. Wayne, “A Polynomial Combinatorial Algorithm for Generalized Minimum Cost Flow,” Proceedings of the 31th Annual ACM Symposium on Theory of Computing, Atlanta, 1-4 May 1999, pp. 19-28.
[11] E. Tardos and K. Wayne, “Simple Generalized Maximum Flow Algorithm,” 7th International Integer Programming and Combinatorial Optimization Conference, Graz, 9-11 June 1999, pp. 1-16.
[12] K. Wayne and L. Fleischer, “Faster Approximation Algorithms for Generalized Flow,” Proceedings of the Tenth Annual ACM-SIAM Symposium on Discrete Algorithms, San Francisco, 1999.
[13] Y. Cui, Y. Xue and K. Nahrstedt, “Max-min Overlay Multicast: Rate Allocation and Tree Construction,” IEEE International Workshop on Quality of Service, Montreal, June 2004.
[14] N. Deo, “Graph Theory with Applications to Engineering and Computer Science,” Prentice Hall Inc., Upper Saddle River, 1994.
[15] R. Cohen and G. Kaempfer, “A Unicast-Based Approach for Streaming Multicast,” Twentieth Annual Joint Conference of the IEEE Computer and Communications Societies, Vol. 1, 2001, pp. 440-448. doi:10.1109/INFCOM.2001.916727
[16] D. Kostic, A. Rodriguez, J. Albrecht and A. Vahdat, “Bullet: High Bandwidth Data Dissemination Using an Overlay Mesh,” Proceedings of the 19th ACM Symposium on Operating System Principles, Vol. 37, No. 5, 2003, pp. 282-297. doi:10.1145/1165389.945473
[17] J. Aspnes, Y. Azar, A. Fiat, S. Plotkin and O. Waarts, “On-line Routing of Virtual Circuits with Applications to Load Balancing and Machine Scheduling,” Journal of the Association for Computing Machinery, Vol. 44, No. 3, 1997. doi:10.1145/258128.258201
[18] B. Awerbuch, Y. Azar, S. Plotkin and O. Waarts, “Competitive Routing of Virtual Circuits with Unknown Duration,” Proceedings of the Fifth Annual ACM-SIAM Symposium on Discrete Algorithms, Philadelphia, 1995, pp. 321-327. doi:10.1145/314464.314508
[19] B. Awerbuch, Y. Azar and S. Plotkin, “ThroughputCompetitive Online Routing,” Proceedings of the 1993 IEEE 34th Annual Foundations of Computer Science, Washington, 1993. doi:10.1109/SFCS.1993.366884
[20] A. Goel, M. Henzinger and S. Plotkin, “Online Throughput-competitive Algorithm for Multicast Routing and Admission Control,” Proceedings of the 9th ACM-SIAM Symposium on Discrete Algorithms, Vol. 5, 1998.
[21] Y. Cui, B. Li and K. Nahrstedt, “On Achieving Optimized Capacity Utilization in Application Overlahy Networks with Multiple Competing Sessions,” 16th annual ACM Symposium on Parallel Algorithms and Architectures, Barcelona, 27 - 30 June 2004, pp. 11-19.
Appendix: Proof of Theorem 1
The proof of Theorem 1 follows the proofs of the following lemmas. We denote OPT as the optimal value of the problem (5).
Lemma 1: MultiTrees-General terminates after at most 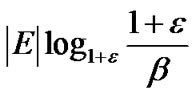 iterations.
iterations.
Proof: Let us consider any edge e∈ε. Initially, de = β. The last time the length of e is updated, it is on a overlay spanning tree t whose length is less than
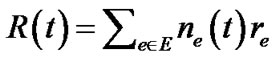 , and is increased by at most a factor of 1 +
, and is increased by at most a factor of 1 + . Since every augmentation increases the length of some edge by a factor of at least 1 +
. Since every augmentation increases the length of some edge by a factor of at least 1 +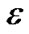 , and R(t) ≤|V|, the number of possible augmentations is at most
, and R(t) ≤|V|, the number of possible augmentations is at most
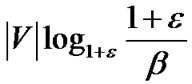 .
.
Lemma 2: Scaling the final flow by 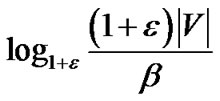 yields a feasible primal solution.
yields a feasible primal solution.
Proof: In the ith iteration of the algorithm, the total flow on an edge e∈εincreases by a fraction 0 ≤ γ(i) ≤ 1 of its capacity. Its length de is multiplied by 1 + γ(i). Since (1+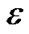 γ(i)) ≥ (1+
γ(i)) ≥ (1+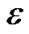 )γ(i) when 0 ≤γ(i) ≤ 1, we have Πi(1+
)γ(i) when 0 ≤γ(i) ≤ 1, we have Πi(1+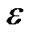 γ(i)) ≥ (1+
γ(i)) ≥ (1+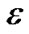 )Σi γ(i) . Thus, every time the flow on e increases by its capacity, its length de increases by a factor of at least (1 +
)Σi γ(i) . Thus, every time the flow on e increases by its capacity, its length de increases by a factor of at least (1 +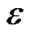 ). Since de is initialized as β, and ends up at most (1 +
). Since de is initialized as β, and ends up at most (1 +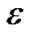 ) |V|, its total flow cannot exceed
) |V|, its total flow cannot exceed
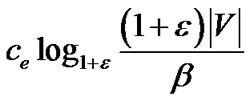 .
.
Lemma 3: When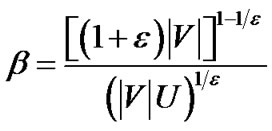 , the final flow scaled by
, the final flow scaled by 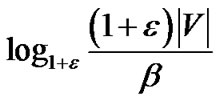 has a value at least (1- 2
has a value at least (1- 2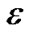 )
)
times OPT. U is the length of the longest unicast route.
Proof: We make the following denotations. Regarding a set of edge length assignments de (e ∈ε), the objective function in problem (7) is 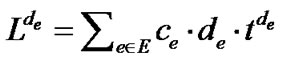 is the minimum overlay spanning tree in terms of de – re. We denote
is the minimum overlay spanning tree in terms of de – re. We denote  as the length of tde in terms of solely de.
as the length of tde in terms of solely de.
The objective of problem (7) is to minimize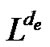 , subject to the constraint that
, subject to the constraint that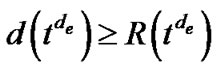 . This constraint can be easily satisfied if we scale the length of all edges by
. This constraint can be easily satisfied if we scale the length of all edges by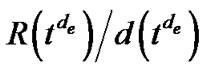 . So problem (7) is equivalent to finding a set of edge lengths, such that
. So problem (7) is equivalent to finding a set of edge lengths, such that 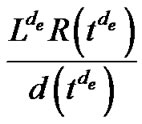 is minimized. Thus the optimal value of problem (7) is
is minimized. Thus the optimal value of problem (7) is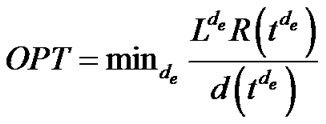 .
.
In each iteration of the algorithm, the length of an edge is updated. We use 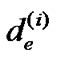 to denote the length of e after the ith iteration.
to denote the length of e after the ith iteration. 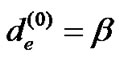 is the initial weight of de. Regarding
is the initial weight of de. Regarding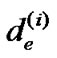 , we simplify the following denotations L
, we simplify the following denotations L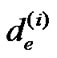 , t de (i) and d(t de (i)), into
, t de (i) and d(t de (i)), into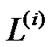 ,
, 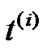 and
and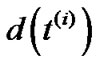 . We also denote f(i) as the total flow that has been routed after the ith iteration. Then based on the edge length update function (Line 10 in Table 7), we have
. We also denote f(i) as the total flow that has been routed after the ith iteration. Then based on the edge length update function (Line 10 in Table 7), we have
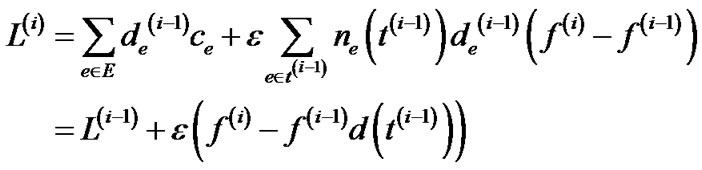
which implies that
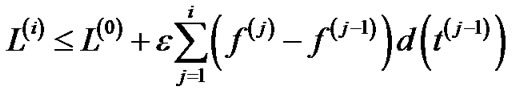 (22)
(22)
Now let us consider the length function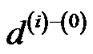 ), i.e., for each edge e ∈ E, its length is
), i.e., for each edge e ∈ E, its length is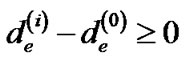 , since the length function is monotonically increasing. Thus, we have
, since the length function is monotonically increasing. Thus, we have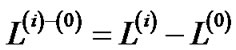 . Since
. Since 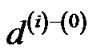 and
and 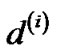 only differs by the constant β at each edge,
only differs by the constant β at each edge, 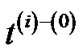 and
and 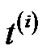 are the same tree. In addition, the length of the tree using
are the same tree. In addition, the length of the tree using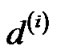 ) versus
) versus 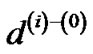 differs by at most β|V|U, U being the length of the longest unicast route. Hence
differs by at most β|V|U, U being the length of the longest unicast route. Hence
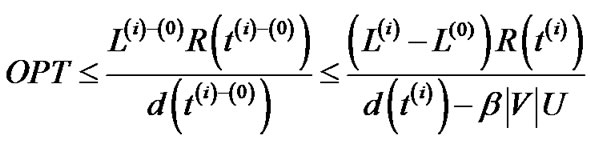
Substituting this bound on L(i) – L(0) in Equation (22) gives
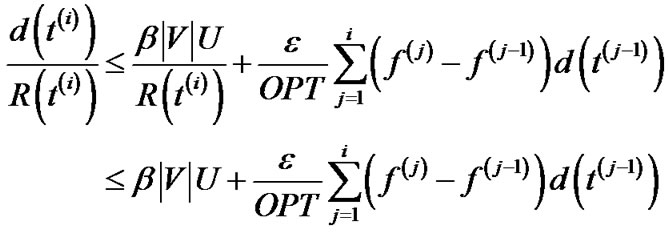
since .
.
Observe that, for fixed i, this right hand side is maximized by setting  to its maximum possible value, for all
to its maximum possible value, for all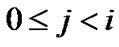 . Let us call this maximum value
. Let us call this maximum value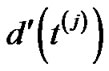 . Hence
. Hence
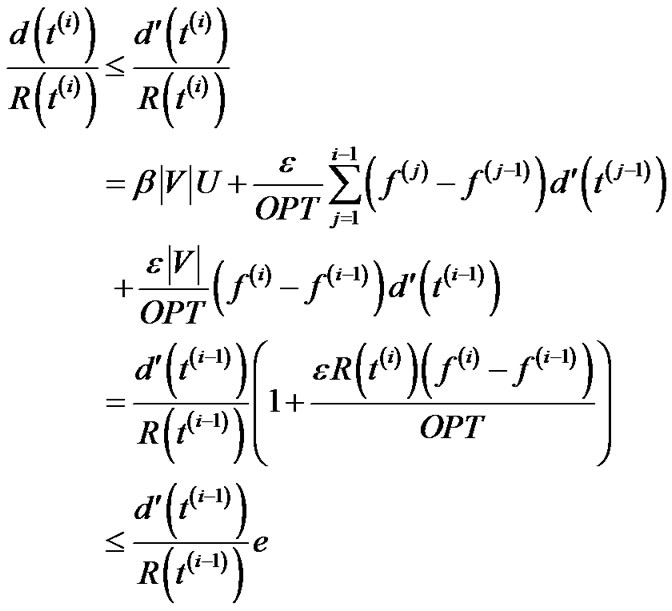
Since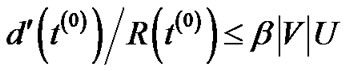 , this implies that
, this implies that
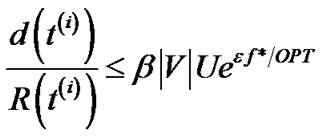
where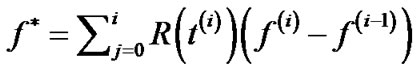 , the objective of problem (7).
, the objective of problem (7).
The algorithm stops when the value of  . Let f∗ be the total flow routed, we have,
. Let f∗ be the total flow routed, we have,
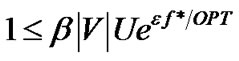
Hence,
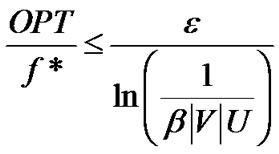
By Lemma 2,  is a feasible solution to problem (7). Then the ratio between the optimal value of problem (7) and the result returned by our algorithm is
is a feasible solution to problem (7). Then the ratio between the optimal value of problem (7) and the result returned by our algorithm is
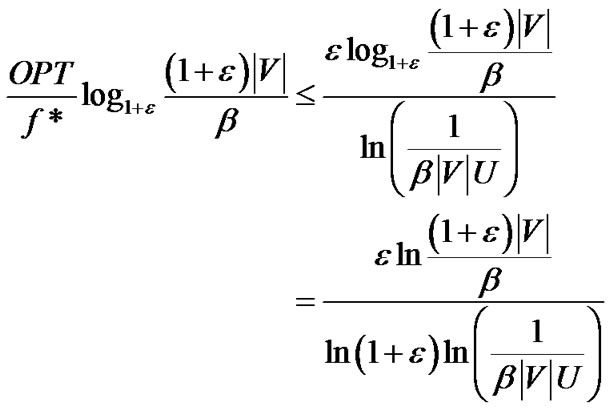 (23)
(23)
when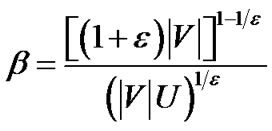 , the above inequality becomes
, the above inequality becomes
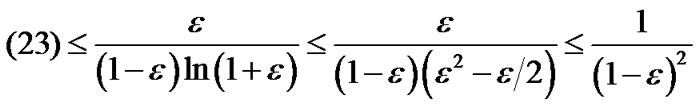
Now we are ready to proof Theorem 1 as follows.
Proof: By Lemma 1, the algorithm terminates after at most 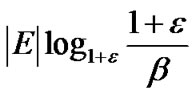 rounds, each round containing a minimum spanning tree construction. When
rounds, each round containing a minimum spanning tree construction. When 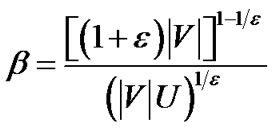 , the maximum number of the iterations needed by the algorithm is
, the maximum number of the iterations needed by the algorithm is
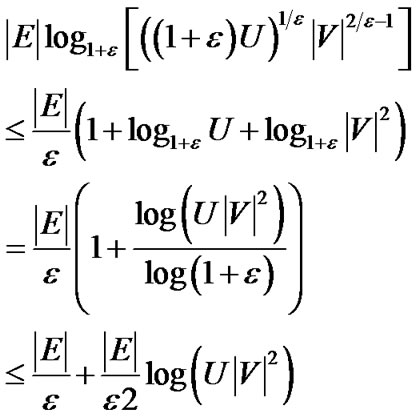
Therefore, the running time is 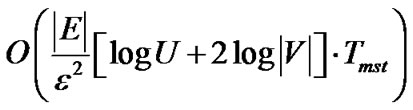 .
.
Appendix: Proof of Theorem 2
Proof: We prove that problem (7), the dual problem of (5) is NP-complete.
The proof is by reduction from the 3-SAT problem. Let F be a 3-SAT formula in conjunctive normal form, where each clause consists of three literals from 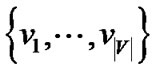 and
and 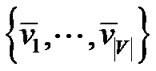 . In Figure 10, we build an overlay network, in which testing if constraint (8) is violated, i.e., the separation oracle of problem (5), corresponds to satisfying assignment of F.
. In Figure 10, we build an overlay network, in which testing if constraint (8) is violated, i.e., the separation oracle of problem (5), corresponds to satisfying assignment of F.
Besides server s, There are two types of peers in this graph. The first type of peers correspond to literals 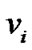 and
and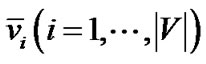 . The second type of peers correspond to clauses of F. All peers have the same resilience factor. The overlay network is a complete graph, whose edges are grouped into two subsets, where edges in each subset carry the same length. Figure 10 only shows all edges with smaller lengths: they direct from s to all literal nodes, between each pair of literal nodes, and from each literal node to each clause node it appears in.
. The second type of peers correspond to clauses of F. All peers have the same resilience factor. The overlay network is a complete graph, whose edges are grouped into two subsets, where edges in each subset carry the same length. Figure 10 only shows all edges with smaller lengths: they direct from s to all literal nodes, between each pair of literal nodes, and from each literal node to each clause node it appears in.
It is obvious that, in terms of the literal set size, there exist an exponential number of minimum spanning trees in this graph, in which all edges have the same length. However, among these trees, we can decide if there exists a tree with the maximum resilience index only by solving the assignment F.
Since all peers have the same resilience factor, the greatest resilience index a peer can get is via the shortest path from s to itself. This is straightforward for literal nodes since s has a direct edge to each of them. A clause node will have to connect to s either through a literal node directly (two-edge path), or through a pair of literal nodes (three-edge path). Only if F is satisfied can we prove the existence of the minimum spanning tree with the maximum resilience index, in which a two-edge path exists for all clause nodes.
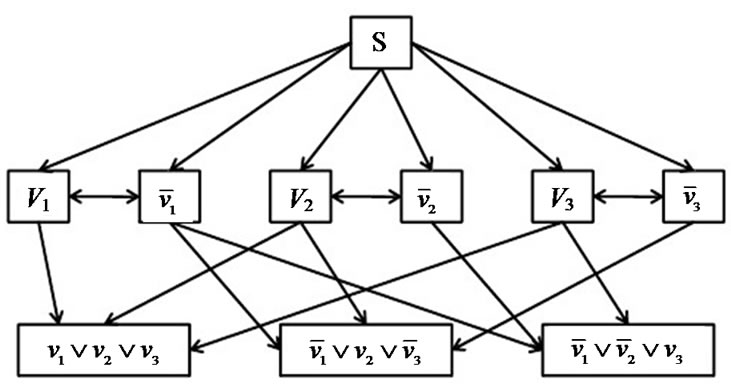
Figure 10. Proof of theorem 2.
Appendix: Proof of Theorem 3
Proof: Our proof consists of two parts. In the first part, we show that any tree can be reorganized into the collection of a subset of the |V| + 1 trees shown in Figure 3 with higher generalized throughput. In the second part, we prove that the tree selection priority the MultiTrees-Star algorithm follows at choosing among these |V| + 1 trees guarantees optimality.
In the first part, we examine an arbitrary tree t, with data flow rate 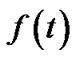 and resilient index
and resilient index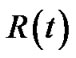 . We introduce a set
. We introduce a set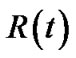 , which consists of all non-leaf nodes in t. It is obvious that
, which consists of all non-leaf nodes in t. It is obvious that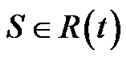 . For each node
. For each node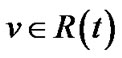 , we denote
, we denote 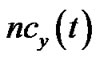 as the number of children v has in t. Then the bandwidth contribution by v is
as the number of children v has in t. Then the bandwidth contribution by v is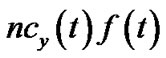 . The resilient throughput contributed by v is the summation of generalized flow received by all its children. Under the non-concatenation model, this value is
. The resilient throughput contributed by v is the summation of generalized flow received by all its children. Under the non-concatenation model, this value is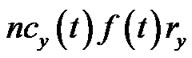 , the product of v’s bandwidth contribution and its resilient factor. Under the concatenation model, this value is
, the product of v’s bandwidth contribution and its resilient factor. Under the concatenation model, this value is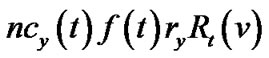 , the product of v’s bandwidth contribution, resilient factor, and resilient index. Under both models, the resilient throughput contributed by the server s is
, the product of v’s bandwidth contribution, resilient factor, and resilient index. Under both models, the resilient throughput contributed by the server s is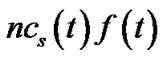 , since the resilience factor of s is 1. As such, t’s resilient throughput
, since the resilience factor of s is 1. As such, t’s resilient throughput 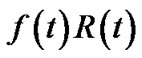 can be considered as the summation of resilient throughput contribution by all nodes in
can be considered as the summation of resilient throughput contribution by all nodes in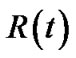 .
.
We now reorganize t as follows. For each peer node v ∈ R(t), we select tree tv in Figure 3, where v is the relaying node. The flow rate of the selected tree is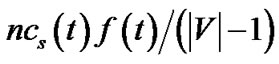 , such that the bandwidth contribution of v equals to its contribution in t. In this tree, the resilient throughput contributed by v is
, such that the bandwidth contribution of v equals to its contribution in t. In this tree, the resilient throughput contributed by v is 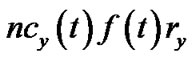 under both concatenation and nonconcatenation models. Compared to the same value in t, v’s resilient throughput contribution in the new tree is higher in concatenation model, and stays the same in non-concatenation model. After conducting the above step for all peer nodes in R(t), the total bandwidth contribution by s would have reached
under both concatenation and nonconcatenation models. Compared to the same value in t, v’s resilient throughput contribution in the new tree is higher in concatenation model, and stays the same in non-concatenation model. After conducting the above step for all peer nodes in R(t), the total bandwidth contribution by s would have reached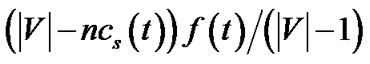 , which is also its resilient throughput contribution. To consume the bandwidth still left at s, we construct tree t0, the last tree in Figure 3, with rate
, which is also its resilient throughput contribution. To consume the bandwidth still left at s, we construct tree t0, the last tree in Figure 3, with rate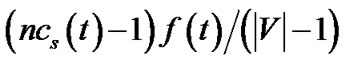 . Since s must have at least one child to ensure connectivity, this value is no smaller than 0. Then s’s bandwidth contribution, as well as its resilient throughput contribution, adding over all trees constructed, is
. Since s must have at least one child to ensure connectivity, this value is no smaller than 0. Then s’s bandwidth contribution, as well as its resilient throughput contribution, adding over all trees constructed, is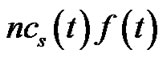 . This value stays the same as in t under both concatenation and non-concatenation models. Now we can claim that, with the above reorganization, the generalized throughput contribution by each node in R(t) is greater or equal to its contribution in tree t. Hence collectively, the aggregate generalized throughput of these trees is greater or equal to the generalized throughput of t, with the same bandwidth contribution by each node in R(t).
. This value stays the same as in t under both concatenation and non-concatenation models. Now we can claim that, with the above reorganization, the generalized throughput contribution by each node in R(t) is greater or equal to its contribution in tree t. Hence collectively, the aggregate generalized throughput of these trees is greater or equal to the generalized throughput of t, with the same bandwidth contribution by each node in R(t).
As it is now clear that the 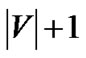 trees shown in Figure 3 collectively achieve higher generalized throughput than any other tree, we proceed to the second part of our proof. Each tree tv except t0 only consumes the bandwidth of s and the relaying peer v, and has its rate upper bounded by the minimum of
trees shown in Figure 3 collectively achieve higher generalized throughput than any other tree, we proceed to the second part of our proof. Each tree tv except t0 only consumes the bandwidth of s and the relaying peer v, and has its rate upper bounded by the minimum of 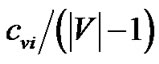 and the remaining bandwidth of s. t0 consumes solely the bandwidth of s. As such, the bandwidth of s becomes bottleneck resource that all trees rely on. We introduce the “gain ratio” for each tree, which is the ratio of its generalized throughput and the bandwidth contribution by s. For all trees except t0, such value is
and the remaining bandwidth of s. t0 consumes solely the bandwidth of s. As such, the bandwidth of s becomes bottleneck resource that all trees rely on. We introduce the “gain ratio” for each tree, which is the ratio of its generalized throughput and the bandwidth contribution by s. For all trees except t0, such value is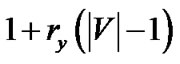 , where rv is the resilience factor of the relaying peer v. For the last tree t0, such value is
, where rv is the resilience factor of the relaying peer v. For the last tree t0, such value is . The tree selection of MultiTrees-Star is based on the descending order of their gain ratios. It is now clear that the algorithm follows a greedy strategy, in each round the tree with the highest gain ratio is chosen and fed with the maximum achievable rate, until the bandwidth of s is depleted.
. The tree selection of MultiTrees-Star is based on the descending order of their gain ratios. It is now clear that the algorithm follows a greedy strategy, in each round the tree with the highest gain ratio is chosen and fed with the maximum achievable rate, until the bandwidth of s is depleted.
Appendix: Proof of Theorem 4
Proof: Our proof consists of three parts. First, we show that the rate returned by MaxRate-Star is feasible to construct a tree. Second, we show that given a fixed rate, MostResilientTree-Star constructs the tree with the maximum generalized throughput. Third, we show that the number of iterations by SingleTree-Star is bounded by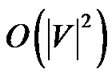 .
.
MaxRate-Star works in a trial-and-error fashion. In line 2, it sets the rate f to cs, the uplink bandwidth of the server, which the maximum possible value for f. From line 3 to 9, it finds sum, the total number of children that the server and all peers can support. If it is smaller than the target value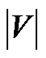 , a smaller value of f will be tried until sum ≥
, a smaller value of f will be tried until sum ≥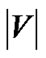 . Since the value of m will advance by at least 1 in each iteration, the algorithm runs in no more than
. Since the value of m will advance by at least 1 in each iteration, the algorithm runs in no more than  iterations.
iterations.
Next, MaxRate-Star constructs a tree by the given streaming rate. It works in a greedy fashion by scheduling the peer with the highest resilience factors to take the maximum number of children it can, starting from the server whose resilience factor is the maximum. Given the definition of a tree’s generalized throughput in the non-concatenation model, the tree constructed will return the highest generalized throughput. The number of peers scheduled by the algorithm is bounded by |V|.
Finally, SingleTree-Star tries different streaming rates from the maximum rate returned by MaxRate-Star to the minimum value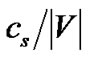 , since any value smaller than that allows the server to stream to all peers, a tree with the maximum resilience index. Since in each iteration, at least one peer’s outbound degree (number of children it can support) will increase by 1, it takes at most
, since any value smaller than that allows the server to stream to all peers, a tree with the maximum resilience index. Since in each iteration, at least one peer’s outbound degree (number of children it can support) will increase by 1, it takes at most 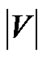 iterations to increase the server’s outbound degree by 1. Therefore, the number of iterations by SingleTree-Star is bounded by
iterations to increase the server’s outbound degree by 1. Therefore, the number of iterations by SingleTree-Star is bounded by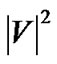 , which makes the running time of MostResilientTree-Star
, which makes the running time of MostResilientTree-Star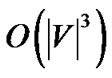 .
.
NOTES
1We note that such categorization does not apply to the management of P2P network, but only suits the purpose of calculating throughput to each peer, which is the main focus of this paper.
1We note that such categorization does not apply to the management of P2P network, but only suits the purpose of calculating throughput to each peer, which is the main focus of this paper.
2We note that unless otherwise notified, our discussion in this section assumes that the inbound bandwidth of each peer v is unbounded, thus removed from the problem formulation. By the end of this section, we will introduce how our algorithms could be adapted to incorporate the inbound bandwidth constraint.

