Advances in Pure Mathematics
Vol.06 No.13(2016), Article ID:73092,4 pages
10.4236/apm.2016.613077
Erratum to “The Riemann Hypothesis-Millennium Prize Problem” [Advances in Pure Mathematics 6 (2016) 915-920]
A. A. Durmagambetov
L. N. Gumilyov Eurasian National University

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 12, 2016; Accepted: December 25, 2016; Published: December 28, 2016
The original online version of this article (Durmagambetov, A.A. (2016) The Riemann Hypothesis-Millennium Prize Problem. Advances in Pure Mathematics, 6, 915-920. 10.4236/apm.2016.612069) unfortunately contains a mistake. The author wishes to correct the errors in Theorem 2 of the result part.
2. Results
These are the well-known Abel’s results.
Theorem 1. Let the function  be limited on every finite interval, and
be limited on every finite interval, and 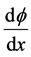 (x) is
(x) is
continuous and limited on every finite interval then
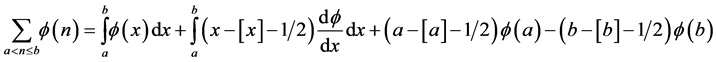 (1)
(1)
Corollary 1. Let the function ,
,  ,
, 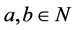 then
then
 (2)
(2)
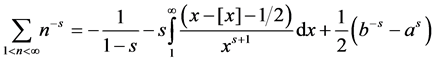 (3)
(3)
Our goal is to use this theorem on the analogs of zeta functions. We are interested in the analytical properties of the following generalizations of zeta functions:
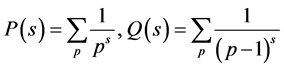 (4)
(4)
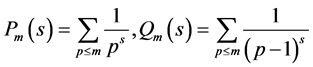 (5)
(5)
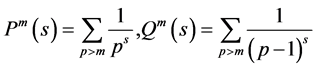 (6)
(6)
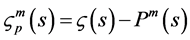 (7)
(7)
Let N be the set of all natural numbers and 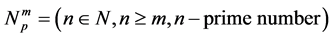
 ―the set of all natural numbers without
―the set of all natural numbers without 
Below we will always let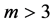 , this limitation is introduced only to simplify the calculations. Considering all the information above let us rewrite
, this limitation is introduced only to simplify the calculations. Considering all the information above let us rewrite

For the function  let us apply the results obtained by Muntz for the zeta function representation. With the help of the given definitions we formulate the analog of Muntz theorem.
let us apply the results obtained by Muntz for the zeta function representation. With the help of the given definitions we formulate the analog of Muntz theorem.
Lemma 1. Let the function
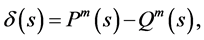 then (8)
then (8)

PROOF: According to the theorem conditions we have

Lemma 2. Let the function

then




PROOF: Follows from computing of integrals.
Lemma 3. Let the function





PROOF: Computing the sums , we have

Theorem 2. Let the function




PROOF: Using Corollary 1. we have






From the last equation we obtain the regularity of the function 
Theorem 3. The Riemann’s function has nontrivial zeros only on the line
PROOF: For

Applying the formula from the theorem 2

estimating by the module

Estimating the zeta function, potentiating, we obtain

According to the theorem 1 

similarly, applying the theorem 2 for 



These estimations for 






