Received 5 February 2016; accepted 25 July 2016; published 28 July 2016

ABSTRACT

For an odd prime number p, and positive integers k and, we denote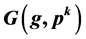, a digraph for which 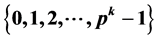is the set of vertices and there is a directed edge from u to v if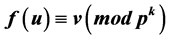, where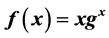. In this work, we study isolated and non-isolated fixed points (or loops) in digraphs arising from Discrete Lambert Mapping. It is shown that if , then all fixed points in 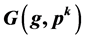are isolated. It is proved that the digraph has 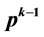isolated fixed points only if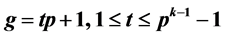. It has been characterized that 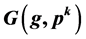has no cycles except fixed points if and only if either g is of order 2 or g is divisible by p. As an application of these loops, the solvability of the exponential congruence 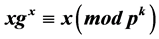has been discussed.

Keywords:

Fixed Points, Lambert Map, Multiplicative Order

1. Introduction

The Lambert W functions are used to find solutions of such equations in which the unknown also appears in

exponential (or logarithmic) terms. It is defined as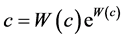, where c is a complex number. Equivalently, it can be defined as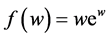. Lambert solved a Diophantine equation 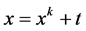in 1758 (see [1] ). Later,

the solution is expressed in term of series. In 1980, the Lambert function was stored in MCAS (Maple Computer Algebra System) as a function for the solution of algebraic equations involving exponential (or logarithmic) functions (see [2] ). In this work, we discussed solutions of such functions by means of their digraphs using residue theory from number theory.

Let be the ring of residue classes modulo. Define by, the discrete Lambert mapping, where. We investigate this mapping using directed graphs whose vertices are residues modulo with edges from to if and only if. This digraph is denoted by.

We investigate self loops (fixed points) of these digraphs and also lift up the investigations of such digraphs by Jingjing Chen and Mark Lotts in [3] from modulo a prime p to modulo. Results regarding fixed points, isolated points followed by astute proofs have been presented. It is important to note that all solutions of congruences of Lambert functions are difficult to find since such mappings are hard to invert and need enormous inversions in any computer algorithm. To understand the terminology and symbols, we follow [3] - [6] .

Definition 1. (see [7] ). Let p be prime and a be any integer not divisible by p. A least positive integer r such that is called order of a modulo. It is denoted as.

Theorem 0. (see [3] ). Let q be any prime and. Then,

1. Let g be a quadratic residue of q, then.

2. A point t is fixed Û.

3. Fixed points of f are multiples of the order of g.

4. Let. If t is odd, then, and if t is even, then is a fixed point.

Let’s draw a digraph of the Lambert map. Take and chose a composite modulus m as. We see that the digraph (see Figure 1) has six loops (fixed points) of which three are non-isolated. The digraph has two non-isomorphic components.

2. Fixed Points of the Map

Recall that a vertex u is said to have a loop ( fixed point) on it if and it referred to as an isolated fixed point of the graph if and there does not exist any vertex v such that. In this section, we present some results to find fixed points (or loops) and isolated points of the graph.

Lemma 1. Let p be any prime. Then, if and only if for any integer g.

Proof. Let. Then 2 is the least positive integer such that. This means that either or. But the first implies that,. Hence. Since. Thus. Conversely, it is easy to see that.

,

The proof of the following theorem is simple and can be established similar to Theorem 0 (4).

Theorem 1. Let and f be Discrete Lambert Map. If a is any odd residue of then and if a is an even residue of then under f.

In the following theorem, we find the values of g for which the fixed points of the digraph are necessarily isolated. Before proving the assertion, we give the following important lemmas.

Lemma 2. If then are the fixed points of the graph. In particular, the vertices, when k is odd and when k is even are always fixed points.

Proof. Let, then for some integer s. But then

(1)

For the rest of the proof, we note that when k is odd and when k is even. Therefore,

The case when k is odd can be dealt in a similar technique. ,

The following Lemma is of crucial importance. However, its proof is simple and can be viewed as a direct consequence of the Definition 1.

Lemma 3. Let g be a residue of. Then if and only if

Proof. Let. Then l is the least positive integer such that. Suppose, then for some integer s such that and. Now

Thus if and only if. But. Hence, we conclude that for. ,

Lemma 4. Let. If divides v then v is a fixed point of the digraph.

Proof. Let. Then is the least positive integer such that. Now for any vertex v, if divides v then for some integer. But then. ,

Theorem 2. If, then all fixed points of are isolated.

Proof. Let. Then by Lemma 3, for. This means that possible orders of g modulo are. Hence by Lemma 4, , for any integer, are the fixed points. We need only to show that these are the possible fixed points and are isolated. Since, so, , where and. Let x be any fixed point in, then. Or

. This means that either or. But. Hence . This clearly shows that x is or multiple of. Finally, we show that these are isolated. Let for some, is adjacent to some. Then. But , so implies that. That is, , which is not possible since ,

Figure 2 depicts Theorems 2 and 3. In Figure 2, we note that. By Theorem 2, the vertices 5, 10, 15, 20 are the fixed points and are isolated. Also is not a multiple of 5, so by Theorem 3, 0 is also an isolated fixed point. Thus all fixed points are isolated.

Theorem 3. Let be a discrete Lambert digraph. Then,

i) If then 0 is the only fixed point of G.

ii) 0 is an isolated fixed point of G if and only if

iii) If is a fixed point then

Proof. i) Let and x be any fixed point of G. Then,

(2)

This means that either or. But, so. Hence (2) yields that, . This is possible only if.

ii) Let On contrary we suppose that there exist a vertex such that x is adjacent to 0. That is,. This means that. But. Hence,

. This certainly implies that. Hence, for some integer k, a contradiction to supposition that. Hence 0 is isolated.

Conversely, suppose 0 is isolated. Let there be any integer k such that and there exist some x such that. Then there must exist some integer such that. This shows that 0 is not isolated, a contradiction. Therefore.

iii) Let be a fixed point together with Then,

This shows that is a primitive root of. But. Thus the word primitive root arrive at a contradiction. ,

The following corollaries are the simple consequences of above theorem.

Corollary 1. Let be the set of vertices in. If then the digraph has no fixed point.

Corollary 2. If then is not a fixed point.

Theorem 4. The digraph contains no cycles except fixed points if and only if either g is of order 2 or g is divisible by p.

Proof. By Lemma 1, if and only if for any integer g. Also by Theorem 1, if and x is odd then otherwise. We claim that there exist no cycle of length 2. For otherwise, an odd vertex a must mapped onto (say), which is of course even and hence b can never adjacent to a since, being even, a contradiction. Thus there does not exist any cycle of length > 1. Now if g is a multiple of p then it is trivial that all vertices constitute one component. Also by Theorem 3(i), if g is a multiple of p then 0 is the only fixed point. Thus the digraph must be a tree with root at 0. Consequently contains no cycle of length > 1. ,

In Figure 3,. By Theorem 4, 0 is the only isolated fixed points.

3. Applications

In recent years, studying graphs through different structural environments like groups, rings, congruences has become much captivating and dominant field of discrete mathematics. These assignments are easy to handle most of the mathematics which is integral based. A variety of graphs have been introduced and characterized regarding their structures through this dynamism. By means of congruences one can inspect numerous enthralling topographies of graphs and digraphs. Thus it becomes interesting to demonstrate that every congruence can generate a graph and hence under certain conditions on these graphs, the nature and solutions of congruences can be discussed. In this section, we discuss the solvability of the congruence and enumerate their solutions using the results given in previous section. The non-trivial ( other than) solution of the congruence modulo a single prime p is easy to discuss since every is prime to p. So the congruence is solvable if and only if as given in Theorem 0 (4). Hence by Fermat's Little Theorem, the number becomes a solution of. Now if we lift up the modulo from p to its higher powers, then the vertices which are not prime to p must not follow the fashion as for.

The following result tackle this case and enumerate the solutions as well. Note that the vertex is the trivial solution in either case. The proof of the following theorem is simple and can be established using results given in Section 2.

Theorem 5. Let p be an odd prime and. Then the following hold:

1. If then the congruence is solvable.

2. Let be any integer. If then the congruence is solvable.

In particular, all are its solutions.

3. If g is a primitive root of then congruence has a unique non-trivial solution.

Thus, 0 and are the only solutions of.

4. If, then the congruence has no non-trivial solution.

Acknowledgements

We are very thankful to the editor and the reviewers for specially sparing their precious time and forwarding useful comments. We sincerely believe that this has made the manuscript more interesting and informative.

Cite this paper

M. Khalid Mahmood,Lubna Anwar, (2016) Loops in Digraphs of Lambert Mapping Modulo Prime Powers: Enumerations and Applications. Advances in Pure Mathematics,06,564-570. doi: 10.4236/apm.2016.68045

References