Advances in Pure Mathematics
Vol.04 No.12(2014), Article ID:52798,1 pages
10.4236/apm.2014.412077
Erratum to “Weierstrass’ Elliptic Function Solution to the Autonomous Limit of the String Equation of Type (2,5)” [Advances in Pure Mathematics 4 (2014), 494-497]
Yoshikatsu Sasaki
Department of Mathematics, Hiroshima University, Higashi-Hiroshima, Japan
Email: sasakiyo@hiroshima-u.ac.jp
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 June 2014; revised 3 July 2014; accepted 15 July 2014
The original online version of this article (Sasaki, Y. (2014) Weierstrass’ Elliptic Function Solution to the Autonomous Limit of the String Equation of Type (2,5). Advances in Pure Mathematics, 4, 494-497. http://dx.doi.org/10.4236/apm.2014.48055 ) was published in August, 2014. Unfortunately, it contains several mistakes. The author wishes to correct the following errors in [1] :
P. 494, L. 7-: The string equation of type (q, p) should be correctly read as
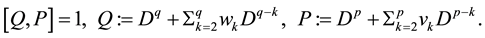
P. 496, L. 13 - 14: Theorem B should be correctly read as follows:
Theorem B. The autonomous limit Equation (A) has a solution concretely described by the Weierstrass’ elliptic function as
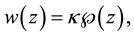
where 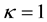 or 3.
or 3.
P. 496, L. 17: In Remark, g2 and g3 in the elliptic function theory should be correctly read as follows:
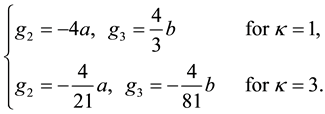
P. 496, L. 21: In the r.h.s. of Equation (1), “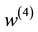 ” should be correctly read as “
” should be correctly read as “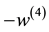 ”.
”.
P. 496, L. 3- - P. 497, L. 2: These 5 lines should be correctly read as follows:
If both of (2) and (3) are valid, then 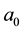 must vanish and
must vanish and 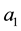 coincides with 4 or
coincides with 4 or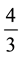 .
.
Case 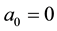 and
and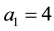 : In this case, we immediately obtain
: In this case, we immediately obtain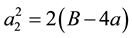 ,
,  ,
,
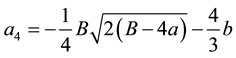 , where
, where 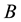 is a root of
is a root of . Inversely, if these are sa-
. Inversely, if these are sa-
tisfied, both of (2) and (3) are valid. 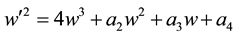 can be reduced to
can be reduced to 








integral constant 

Case 
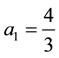




allowed as the integral constant c in the r.h.s. of (2). Inversely, if these are satisfied, both of (2) and (3) are valid.




References
- Sasaki, Y. (2014) Weierstrass’ Elliptic Function Solution to the Autonomous Limit of the String Equation of Type (2,5). Advances in Pure Mathematics, 4, 494-497. http://dx.doi.org/10.4236/apm.2014.48055

