Advances in Pure Mathematics
Vol.4 No.6(2014), Article
ID:47280,3
pages
DOI:10.4236/apm.2014.46036
Time-Domain Analysis of the Periodically Discontinuously Forced Fractional Oscillators
Zdzislaw Trzaska
Warsaw University of Ecology and Management, Warsaw, Poland
Email: zdzislaw.trzaska@netlandia.pl
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 February 2014; revised 19 March 2014; accepted 25 March 2014
ABSTRACT
A new method for the solution of non-sinusoidal periodic states in linear fractionally damped oscillators is presented. The oscillator is forced by a periodic discontinuous waveform and a viscous element is taken into account. The presented method avoids completely the Fourier series calculations of the input and output oscillator waveforms. In the proposed method, the steady-state response of fractionally damped oscillator is formulated directly in the time domain as a superposition of the zero-input and forced responses for each continuous piecewise segments of the forcing waveform, separately. The whole periodic response is reached by taking into account the continuity and periodicity conditions at instants of discontinuities of the excitation and then using the concatenation procedure for all segments. The method can be applied efficiently to discontinuous and continuous non-harmonic excitations equally well. Solutions are exact and there is no need to apply any of the widely up-to-date used frequency approaches. The Fourier series is completely cut out of the oscillator analysis.
Keywords:Fractionally Damped Oscillators, Periodic Non-Smooth Forcing Terms, Non-Sinusoidal Periodic Solutions, Concatenation Procedure

1. Introduction
Mathematical models of dynamical systems with fractional-order derivatives have found many applications in various domains of science and technology such as viscoelasticity, control theory, electronics, heat conduction, electrode-electrolyte polarization, diffusion wave, electromagnetic waves, signal processing and many other physical processes [1] -[8] . In mechanics, for example, fractional-order derivatives have been successfully used to model the damping forces with memory effect or to describe state feedback controllers [9] [10] . Presently, it is clear that the fractional calculus broadens our perception not only of physical processes but also of many biological systems. Studies on dynamical behaviors of the electric signals of a human muscle’s tremor of legs in a normal state and of the electric potentials of the human brain core from EEG’s during epileptic seizure as well as a human hand finger tremor in Parkinson’s disease have attracted considerable attention in many research centers through the world [11] [12] . These systems are known to display fractional-order dynamics (FOD). The characteristic features of all these models are that fractional derivatives introduce a new parameter-the order of fractional derivative n changing the properties of the solutions.
Recently, it is found in [13] that in fractional-order vibration systems of single degree of freedom, the term of fractional-order derivative whose order is between 0 and 2 acts always as damping force. In addition, almost all systems containing internal damping are not suitable to be described properly by the classical methods, but the fractional calculus represents one of the promising tools to incorporate in a single theory both conservative and non-conservative phenomena [14] . It is a well-recognized belief that fractional calculus leads to better results than classical one [15] . In some cases, it is possible to find out closed form solutions of fractional-order differential equations [2] [6] [8] . Therefore, a description of dynamical systems with using fractional derivatives may lead to results of major importance.
The definitions of fractional integral and derivative have been provided in the fractional calculus literature in a variety of ways, including Riemann-Liouville, Caputo, Erdélyi-Kober, Hadamard, Grünwald-Letnikov, and Riesz type. Equivalence of these definitions on some function has also been established [16] -[18] . However, the two most commonly used definitions are the Riemann-Liouville and the Caputo ones. It is well known presently that initial conditions are not taken into account in the same way whether Riemann–Liouville or Caputo definitions are considered. It is worth to mention that several mathematical and physical interpretations of fractional differentiation and of fractional systems exist in the literature [7] [14] . A demonstration of Montseny for a fractional integrator is now adapted to deduce a physical interpretation of a fractional system. From applications point of view the most convenient representation is that that permits to take into account initial condition in a coherent way with system physics.
Note that in the domain of fractional-order dynamical systems, fractional order harmonic oscillator is a fundamental issue, for it can be used to describe a much broader area of application than it is possible with the classical approach. Therefore, it is of fundamental importance to study the fractional model of the harmonic oscillator and to discuss the specific properties of its solutions.
The plan of the paper is the following: Section 2 provides basic formulations and introductory results to be used in this article. Section 3 derives the main problem concerning solutions of fractionally damped oscillators with periodic discontinuous excitations. In Section 4, we give results of applications of the proposed method to determination of T -periodic solution of equations describing fractionally damped oscillator with discontinuities in time periodic excitations. Finally, in Section 5 conclusions are presented.
2. Basic Formulations and Introductory Results
In this section we are focused on the equation of a linearly damped oscillator with the damping term generalized to a Caputo fractional derivative. We deal with the fractional-order differential equations expressed in terms of the Caputo derivatives needing the initial conditions in the same form as for the integer-order differential equations. It is an advantage because applied problems require definitions of fractional derivatives, where there are clear interpretations of initial conditions, which contain f(a), 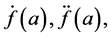 etc. The analytic solution to the fractionally damped equation can be drawn by means of Laplace transform. Note, that the Laplace transform method is a very frequently used tool for solving engineering problems.
etc. The analytic solution to the fractionally damped equation can be drawn by means of Laplace transform. Note, that the Laplace transform method is a very frequently used tool for solving engineering problems.
The existence of periodic solutions is very often a desired property in dynamical systems, constituting one of the most important research directions in applied mathematics, with applications ranging from celestial mechanics to biology and finance. The analysis of linear harmonic fractionally damped oscillator is a very recent and promising research topic.
A standard approach to derive T-periodic solution is to define the differential operator which maps an initial value along the unique solution by T-units. Then the key periodicity and compactness conditions are given such that some fixed point theorems can be applied to get fixed points for the differential operator, which give rise to T-periodic solutions.
In order to study periodic responses of a fractionally damped oscillator, we consider here the Caputo fractional derivative in the scalar case, introduced in [14] . The considered oscillator is described by the equation
![]() (1)
(1)
where  is the symbol of the derivative,
is the symbol of the derivative, ![]() and
and ![]() denote the response and excitation terms of the oscillator, respectively. Constant coefficients A and B depend on parameters of the oscillator elements and their connections. The fractional order n of the damping term will be restricted to 0 ≤ n ≤ 1.
denote the response and excitation terms of the oscillator, respectively. Constant coefficients A and B depend on parameters of the oscillator elements and their connections. The fractional order n of the damping term will be restricted to 0 ≤ n ≤ 1.
The forcing term is assumed to be periodic discontinuous function of time t with finite number of discontinuities over period T. Using the concatenation procedure we represent the forcing term as splines of continuous segments (Figure 1).
For instance, the forcing term shown in Figure 1 can be represented as follows
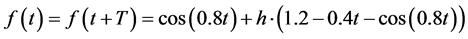 (2)
(2)
where  denotes the concatenation factor with p = p(t) = p(t + T) as the socalled saw tooth function [19] .
denotes the concatenation factor with p = p(t) = p(t + T) as the socalled saw tooth function [19] .
It is worth pointing out that formula (2) can be easily extended on all remaining discontinuity points if they exist in the forcing terms. In the sequel we discus properties of fractionally damped oscillators with periodic non-sinusoidal discontinuous excitations and develop a systematic Fourier series-less method for their studies.
3. Preliminary Results
3.1. Analysis of Fractionally Damped Oscillators
In this section, the attention is focused on the linear fractionally damped oscillator characterized by the structure shown in Figure 2. A superconducting coil L with very small resistance R is connected in parallel with a supercapacitor C and controlled source as an active element. The forcing term is represented by independent current source js(t).
Applying Kirchhoff current law and relations between current and voltage for each oscillator element yields
 (3)
(3)
where G denotes the active element conductance and μ and n denote fractional orders characterizing the super
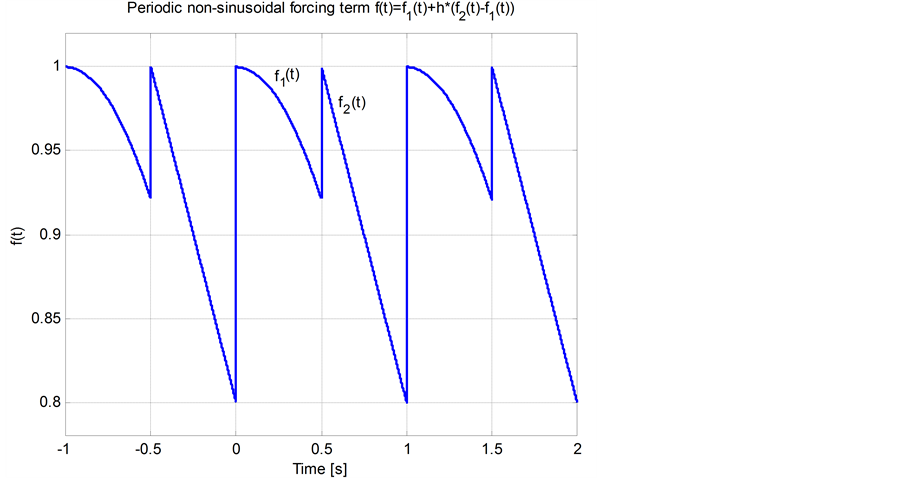
Figure 1. Periodic discontinuous forcing term f(t) = f(t + T).
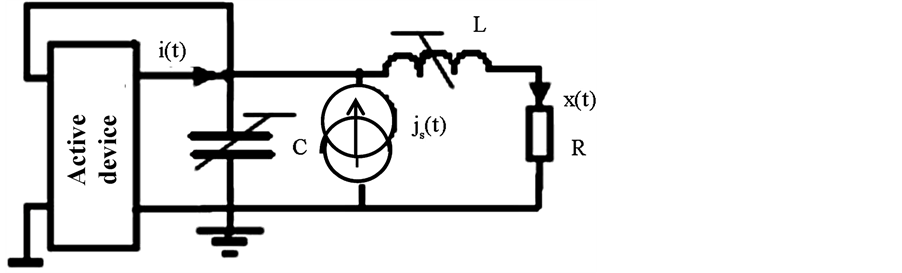
Figure 2. Scheme of the oscillator structure.
capacitor and superconducting coil, respectively. Because in practice the sum of fractional orders is very near two thus in the sequel we take μ + n = 2. Then, after few simple manipulations on the components of Equation (3) we can transform it to the form represented by (1) with
![]() (4)
(4)
In what follows the Equation (1) with notation (4) is considered taking into account the damping term generalized to a Caputo fractional derivative. It is worth mentioning that the Caputo derivative has been often used in fractional order systems since it has the practical initial states like that of integer order systems. Recall that the order of the derivative being considered is 0 ≤ n ≤ 1. At the lower limit (n = 0) the equation represents a no damped oscillator and at the upper limit (v = 1) the ordinary linearly damped oscillator equation is recovered.
Time response of system (1) is thus defined by
![]() (5)
(5)
where xd(t) is the damped component, and xp(t) denotes the periodic component.
In this article, we present a new method suitable for determination of non-sinusoidal periodic response xp(t) of linear fractionally damped oscillator. It avoids the Fourier series calculations of the input and output oscillator waveforms. In the proposed method, the oscillator response is formulated directly in the time domain as a superposition of the zero-input and forced responses for each continuous piecewise segments of the forcing term, separately. The strict periodic response is reached by taking into account the continuity and periodicity conditions at instants of discontinuities of the forcing term and then using the concatenation procedure for all segments.
It is hoped that a careful study of the analytic solution to the linear fractionally damped equation will help shed light on properties of the nonlinear equation and be of use for direct applications of fractionally damped oscillations.
To find an analytic solution we first consider homogeneous form of Equation (1) by annihilation of the forcing term. Thus, we take into considerations the equation
![]() (6)
(6)
In the following, we will present the solutions of this forcing free fractional differential equation for different fractional orders and will investigate the specific differences of the obtained solutions. The analytic solution to the above fractionally damped equation is found by means of Laplace transform.
Using Caputo definition and applying Laplace transformation to both sides of (6) gives
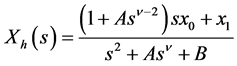 (7)
(7)
with Xh(s) =L[xh(t)] as the Laplace transform of the response of fractionally damped autonomous oscillator and x0 and x1 as initial conditions.
In order to evaluate the inverse Laplace transform of X(s) the following equation needs to be solved
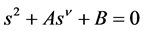 (8)
(8)
what is not a trivial problem for arbitrary n. Substituting s = reia into (8) and then comparing to zero a real and imaginary part yields
 (9)
(9)
Performing detailed examinations of possible solutions of (9) it can be easily verified that for 0 £ n £ 1 there are nine distinct cases as opposed to the usual three for the ordinary oscillator’s equation (damped, over-damped, and critically damped). In three of these cases, the frequency of oscillation actually increases with increasing damping order before eventually falling to the limiting value given by the ordinary damped oscillator equation. For the six remaining cases, the behavior of the fractional oscillator is as expected and the frequency of oscillations decreases with increasing order of the fractional derivative. Observe moreover, that both terms of the second Equation in (9) would always be positive, thus, there are no solutions in the right half of the complex plane and none on the complete axis of negative real numbers. If there are solutions, they should be in pairs, complex conjugates, with π/2 < a < π and −π/2 > a > −π. Thus, Equation (8) can be rewritten in the form
![]() (10)
(10)
with ![]() and
and ![]() where r1 > 0 and p/2 < a1 < p denotes solutions of (9). It has to be noted that for the fractionally damped equation repeated roots are not possible.
where r1 > 0 and p/2 < a1 < p denotes solutions of (9). It has to be noted that for the fractionally damped equation repeated roots are not possible.
The time response of system (6) is thus given by
![]() (11)
(11)
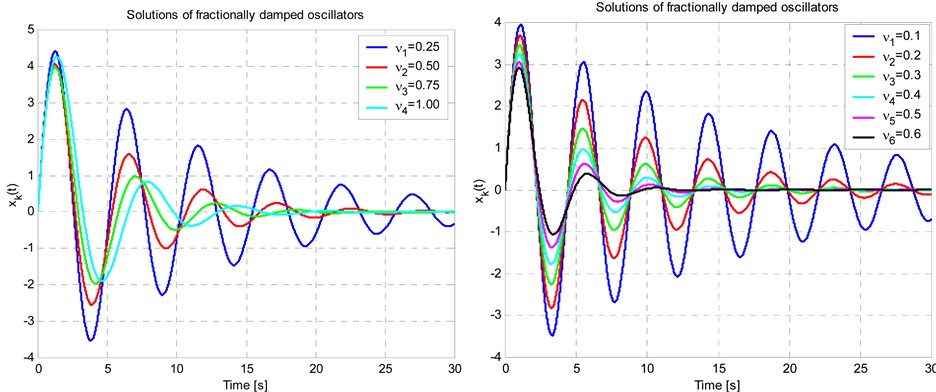
where C1 and C2 are constant. In Figure 3 are presented some graphs of solutions (11) for fixed A=0.5 and B =1.0, and various values of ν.
It should be emphasized that the evolution in time for this system is dominated by an exponential decay. Consequently, we obtain the result, that the behavior of the free solutions of the fractional harmonic oscillator under variation of the fractional derivative order n may be interpreted from a classical point of view as damping phenomena. Our view point sheds some new light on the arising question: does the oscillation frequency fall monotonically with respect to n? To demonstrate an answer we first examine the derivative of (8) with respect to n and get
 (12)
(12)
Denoting s = a + iw and separating the imaginary part of (12) yields
 (a) (b)
(a) (b)
Figure 3. Solutions of the fractionally damped oscillator with: (a) n = 0.25, 0.5, 0.27, 1.0; (b) n = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6.
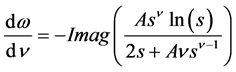 (13)
(13)
Considering this expression at ν = 0 we get initial slopes for the rate of change of w with respect to ν as follows
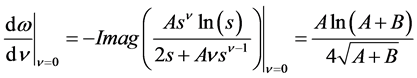 (14)
(14)
Note that (14) generates three main cases of the initial slopes, namely 1) The frequency initially increases with increasing damping order for A + B > 1;
2) The frequency initially is not changing with increasing damping order for A + B = 1;
3) The frequency initially decreases with increasing damping order for A + B < 1.
The above result indicates that there are nine cases for the linear fractionally damped oscillator because in each of the main cases can become any of the three particular cases, i.e., damped, over-damped, and critically damped. A surprising result lies in that that for three of the particular cases the oscillation frequency actually increases with increasing order of derivative of the damping term. After reaching a peak value, the frequency decreases as expected.
3.2. Fourier Series-Less Representation of Periodic Discontinuous Functions
In this subsection, we introduce notations, definitions, and preliminary facts, which are used throughout the remaining part of this paper. The representations introduced in the next section permits to take into account periodicity and continuity conditions of the permanent response of a fractionally damped oscillator in a coherent way with system physics. The main attention focuses on periodic discontinuous functions.
It is well known that a discontinuous function, like the square or saw-tooth waveforms, cannot be expressed as a sum, even an infinite one, of continuous functions. The extraneous peaks in the square wave’s Fourier series never disappear; because they occur whenever the function is discontinuous, and will always be present whenever the function has jumps [20] [21] . Quite obviously, if the excitation waveform is subject to jump changes the linear smoothing procedure is not a good choice anymore, because all conservative oscillator elements confuse and remove the high frequency components from the circuit output. For this reason, when a source waveform with jumps is applied to a linear oscillator it causes a typical effect of “edge blurring”.
The main theorem concerning the convergence of the Fourier series at a discontinuity implies that this series converges to f(t) except at the point t = t0, which is a point of discontinuity of f(t). Indeed, Gibbs [22] showed that if f(t) is piecewise smooth on ![]() and t0 is a point of discontinuity, then the Fourier partial sums will exhibit the same behavior, with the bump's height almost equal to
and t0 is a point of discontinuity, then the Fourier partial sums will exhibit the same behavior, with the bump's height almost equal to
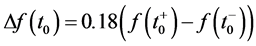 (15)
(15)
Recall that the notations 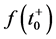 and
and 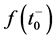 represent the right-limit and left-limit, respectively, of f(t) at the point
represent the right-limit and left-limit, respectively, of f(t) at the point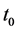 .
.
Thus, it is evident that for accurate analysis of fractionally damped oscillators excited by forcing terms producing complicated harmonic components, more formal time-domain mathematical tools are needed.
Taking into account the above requirements and insufficiencies of the methods based on Fourier series, which are up-to-date most commonly used for studies of periodic non-sinusoidal states of linear as well as nonlinear oscillators we propose in the sequel new method for obtaining, in closed form, the response of any linear oscillator corresponding to piecewise-continuous periodic non-sinusoidal forcing terms. The Fourier series-less method presented here depends on a “saw-tooth waveform” and of a scheme for the unified representation of composite periodic non-sinusoidal waveforms. It appears as a powerful broadly applicable technique that enables us to characterize non-harmonic periodic oscillations from a perspective different from that obtained by the method resulting from the Fourier series.
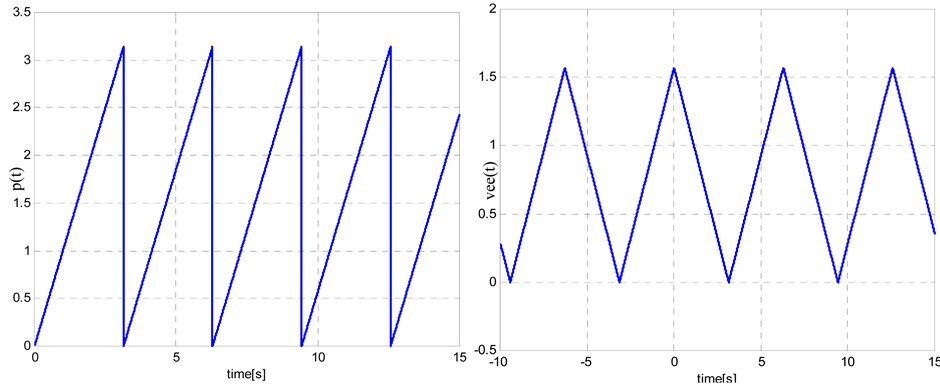
To avoid the difficulty appearing in practical applications of the Fourier series to obtain exact solutions of problems involved by periodic non-sinusoidal forcing terms operating in linear fractional order oscillators, we propose to use a so-called period carrying waveform p(t) defined as follows
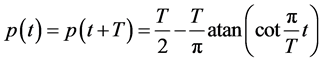 (16)
(16)
where T denotes the period. The direct plot of (16) for T = p seconds is presented in Figure 4(a), and very often is called “saw-tooth function” or equivalently “saw-tooth waveform”. Applying p(t) it is easy to generate a periodic form of the well known absolute value function called also “vee” function which can be defined as follows
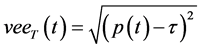 (17)
(17)
The plot of (17) for T = 2π seconds and τ = π seconds is presented in Figure 4(b).
In the sequel we will also take advantages of such useful functions as:
relay function r(t,τ) also called jump function which can be defined by
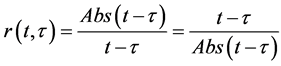 (18)
(18)
The plot of function (18) depending on p(t), i.e. r(p(t),τ) for τ = π seconds is shown in Figure 5(a).
The switch-on function denoted by h(t,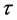 ) is defined as follows
) is defined as follows
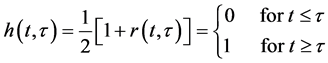 (19)
(19)
The plot of function (19) depending on p(t), i.e. h(p(t),τ) for τ = π seconds is shown in Figure 5(b).
The above waveforms as well as many other similar ones, which can be easily derived on their base, are very useful in relatively simple representations of composite periodic non-sinusoidal waveforms. We remark that the latter situation will be relevant in the present analysis.
However, in a general setting, i.e., when we are dealing with waveforms x(t) exhibiting discontinuities, two restrictions must be fulfilled, namely: (i) global condition requiring that x(t) is absolutely integrable, (ii) local condition constraining x(t) to have a finite number of maxima and minima and a finite number of discontinuities in every finite interval [15] [22] . Moreover, we will use the results known in the general statement for the special case of the concatenation and show that this leads to an elegant procedure in Fourier series-less analysis also in the situation of real jumps in the input as well as output waveforms.
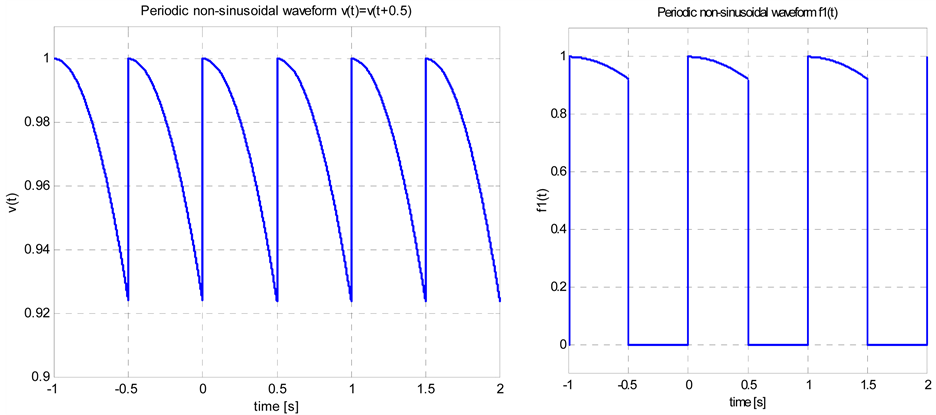
To cope with these effects we will describe discontinuous functions by using the saw-tooth waveform and its relatives such as switch-on and relay waveforms. To present the main idea of such an approach we consider at first a periodic non-sinusoidal function v(t) = v(t + T) with T = 0.5 seconds as the period. Such type of wave
 (a) (b)
(a) (b)
Figure 4. Diagrams of periodic functions: (a) p(t); (b) veeT(t).
forms appears very often in power electronics [22] -[29] . Its diagram is shown in Figure 6(a) and can be represented by
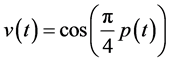 (20)
(20)
with
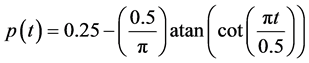 (21)
(21)
as the period carrying waveform.
Further, the waveform f(t) = f(t + 1) shown in Figure 6(b) can be represented using the switch-on waveform h(t,τ) with τ = T/2 = 0.5 seconds as follows
 (a) (b)
(a) (b)
Figure 5. Diagrams of periodic discontinuous functions: (a) r(t); (b) h(t).
 (a) (b)
(a) (b)
Figure 6. Periodic discontinuos functions: (a) v(t) = cos(pp(t)/4) and T = 10.5 s; (b)  for
for 
 .
.
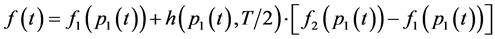 (22)
(22)
where
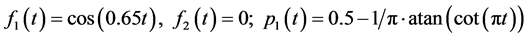 (23)
(23)
The above examples show that the new proposed harmonic-less approach is very effective and leads to much less time consuming task than the standard method following from the Fourier series analysis. This intuitively appealing “switching rule” can be exploited in several ways. Using the switching approach (22) suggests the incorporation of a true smoothing element into the competition.
4. General Analysis of Forced Fractional Oscillators
4.1. Periodic Closed-Form Response
The purpose of this section lies in demonstrating how to generate and analyze complex form responses of linear systems under steady states with both discontinuous and continuous periodic non-harmonic forcing terms. As a matter of fact, periodic oscillations are very important and special phenomena not only in natural science but also in social science such as climate, food supplement, insecticide population, sustainable development [29] .
The large applicability of the Caputo fractional derivatives is because we can formulate the fractional differential equations initial conditions as in the case of the classical one. Such particular properties of Caputo derivative as
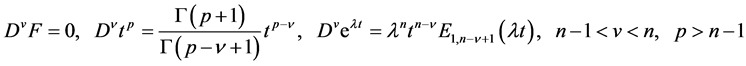 (24)
(24)
where F = const, G(.) is the gamma function and E1,a(.) denotes the two-parameter Mittag-Leffler function, are very useful in general analysis of forced fractional oscillators. The above features of the Caputo derivative have attracted the engineers’ interest in the latter years, and now it is a tool used in almost every area of science.
To determine a periodic response of a fractionally damped oscillator we take into considerations the oscillator shown in Figure 1 in which source currents js(t) represents the periodic discontinuous forcing term. Using notations (4) and approaching the time to the limit t ® ¥ we get
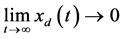 (25)
(25)
so that
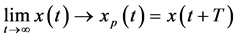 (26)
(26)
and in steady-state the oscillator response fulfills Equation (1) with x(t) = x(t + T) where T denotes the period of the forcing term fT(t) = Bjs(t). Taking into account all particular continuous segments of the discontinuous forcing term we assume the corresponding continuous segment of the oscillator response as follows
![]() (27)
(27)
where s1 and s2 denote solutions of Equation (8), and A1,k and A2,k denote constants to be determined. The last component xf,k(t) takes the quite similar variation in time as that exhibited by the corresponding segment of fT,k(t) of the forcing term for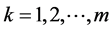 .
.
It has to be emphasized here that the oscillator is composed of a capacitor and an inductor both of fractional orders and they must fulfill the physical law of continuous changes of the capacitor voltage and inductor current. This important feature can be taken into account for determination of constants A1,k and A2,k of all segments of the oscillator response.
In the sequel to maintain only the clarity of the analysis without lost of its generality, we will limit the attention to the forcing current exhibiting time variations shown in Figure 7(a). This form of the forcing current is very often applied in practice for producing electrochemical nanostructural surface layers of appropriate metals or isolators to protect or improve exploitation properties of various construction and machinery details [8] .
It is easily to check that the source current can be represented on the whole time interval by
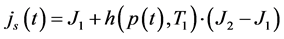 (28)
(28)
 (a) (b)
(a) (b)
Figure 7. Diagrams of: (a) source current; (b) response of fractionally damped oscillator.
where p(t) and h(p(t), T1) are determined by (16) and (19), respectively.
Note that in such a case the excitation current is characterized by two discontinuity moments, i.e. t1 = 0 and t2 = T1 separating two segments of constant values J1 and J2, respectively. The response of the oscillator can be represented for 0 £ t < T1 by
![]() (29)
(29)
for T1 £ t < T by
![]() (30)
(30)
where constants A1, A2, A3 and A4 are to be determined. Components X1 = J1 and X2 = J2 correspond to particular solutions of Equation (1) for appropriate segments of the forcing current. The resulting current in the coil is expressed as follows
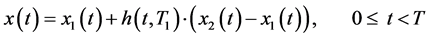 (31)
(31)
In order to determine unambiguously the constants a help comes from the capacitor voltage, which in accordance with the principles of physics must be continuous in the time. So calculating the fractional derivative of the current in the coil, we get a quantity proportional to the capacitor voltage. Hence, taking into account the Caputo derivative for 0 £ n £ 1 yields
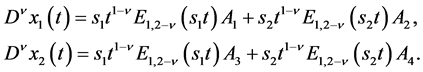 (32)
(32)
Combining continuity and periodicity conditions for (29)-(32), we get a system of equations with unknown A1, A2, A3 and A4. In matrix notation, they take the following form
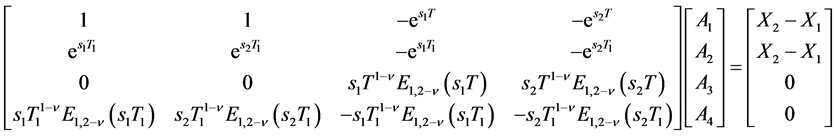 (33)
(33)
where T1 denotes a moment at which exists a discontinuity of the forcing term fT(t). Solving the above equation for following parameters of the fractionally damped oscillator: A = 0.5, B = 1, J1 = 10 A, J2 = −5 A, T = 20 s and T1 = 5 s and then substituting the result into (29)-(31) we get for n = 0.5 the coil current x0.5(t), which is presented in Figure 7(b).
4.2. Computer Simulations
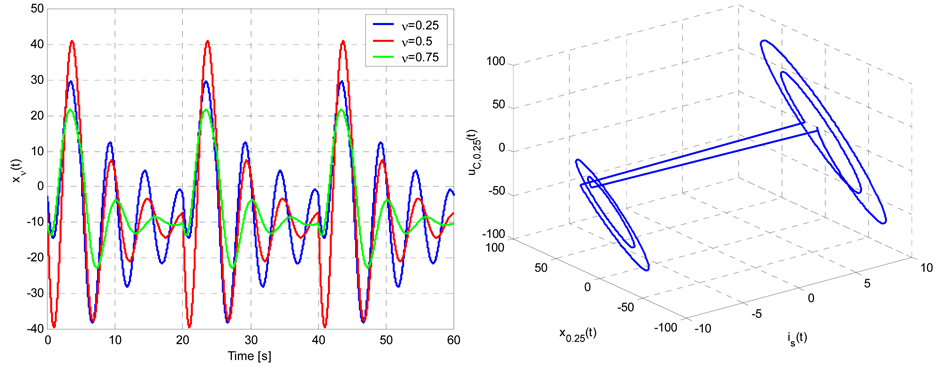
In this subsection, the simulation results are presented to further demonstration of the reliability of the above approach. Three different fractional order systems represented by damped harmonic oscillator equation have been considered to confirm the given analytical results. First, let us use Equations (29)-(31) for n = 0.25, 0.5 and 0.75 for examinations of influences of the fractional order on the response damping within the period of forced fractional oscillator. Moreover, this gives also possibilities to examine the responses of the oscillator on different form of variations in time of the periodic forcing term.
Following the procedure presented in the above subsection, we can generate periodically forced responses of the same oscillator for different fractional orders. We exploit here a numerical technique using Matlab incorporated into the procedure, which is similar to the semi-analytical method. For forcing current exhibiting the discontinuous variations in time shown in Figure 7(a) with J1 = 10A, J2= −10A, T = 20 s and T1 = 10 s simulations were performed for oscillator parameters A = 0.5, B = 1 and fractional damping order: n = 0.25, 0.5 and 0.75, respectively. Results of numerical simulations are presented in Figure 8(a). Observe that the form of the periodic responses differ significantly with respect to that of the forcing term, but this fact agrees very well with physical considerations of the studied problem and the dynamic properties of the given oscillator. Moreover, there is no doubt that fractional order has become an exciting new factor indicating the damping rate of the oscillator. It takes quite similar role as the damping coefficient in the case of classic, i.e. integer order oscillator. When 3D phase trajectory is established (Figure 8(b)) in coordinates (is(t), x0.5(t),![]() ) then it is evident that the oscillations generate a limit cycle with specific form being in good agreement to the physical state of the fractionally damped oscillator. From Figure 8(b), we can see that state loops of x0.5(t) for t Î (0, T1) and t Î (T1, T) are similar to each other, but they are not identically coincided with each other although excitation current exhibits symmetry with respect to time axis. The difference is much more visible with changes of the fractional order n. Thus, it is expected that as in the case of classical oscillation systems, the form of the excitation term and parameters of the oscillator determine completely the evolution of the oscillation systems.
) then it is evident that the oscillations generate a limit cycle with specific form being in good agreement to the physical state of the fractionally damped oscillator. From Figure 8(b), we can see that state loops of x0.5(t) for t Î (0, T1) and t Î (T1, T) are similar to each other, but they are not identically coincided with each other although excitation current exhibits symmetry with respect to time axis. The difference is much more visible with changes of the fractional order n. Thus, it is expected that as in the case of classical oscillation systems, the form of the excitation term and parameters of the oscillator determine completely the evolution of the oscillation systems.
5. Conclusions
This work presents an effective concept of analyzing fractionally damped linear oscillator forced by a discontinuous periodic excitation and feasible computational strategies for time-varying dynamical processes based on continuity and periodicity approach for their solutions. This approach does not use any approximations based on the Fourier coefficient and not needs further investigation.
The relationship between fractional order and the damping of oscillations are discussed and concluded that the fractional order systems cannot be instead of by any other system. The stability criteria of fractionally damped oscillators are addressed. We have revealed that the fractionally damped oscillator contains nine subclasses of
 (a) (b)
(a) (b)
Figure 8. Results of numerical simulations: (a) oscillator responses for n = 0.25, 0.5, 0.75, (b) 3D plot for n = 0.25.
oscillators depending on parameters of elements and the fractional order n.
Methods are also proposed to obtain concatenation of continuous response segments corresponding to continuous segments of the discontinuous forcing term. A physical interpretation of a fractional order of the oscillator damping term is also proposed that demonstrates that any fractionally damped system can be viewed as an integer order system described by an equivalent diffusion term associated to a classical rational linear (exponentially damped) system.
We emphasize that it is possible to obtain exact periodic solutions for the output in periodic fractional-order dynamical systems forced by excitations being discontinuous in time.
References
- Magin, R.L. (2006) Fractional Calculus in Bioengineering. Begell House Publishers, Redding.
- Monje, C.A., Chen. Y., Vinagre, B.M., Xue, D. and Feliu, V. (2010) Fractional-order Systems and Controls: Fundamentals and Applications. Springer, Berlin, New York. http://dx.doi.org/10.1007/978-1-84996-335-0
- Chen, Y.Q., Ahn, H.S. and Podlubny, I. (2006) Robust Stability Check of Fractional Order Linear Time Invariant Systems with Interval Uncertainties. Signal Processing, 86, 2611-2618. http://dx.doi.org/10.1016/j.sigpro.2006.02.011
- Carpinteri, A. and Mainardi, F. (1997) Fractional Calculus: Integral and Differential Equations of Fractional Order. Fractals and Fractional Calculus in Continuum Mechanics. Springer Verlag, Wien and New York, 223-276. http://dx.doi.org/10.1016/j.sigpro.2006.02.011
- Lakshmikantham, V., Leela, S. and Devi, J.V. (2009) Theory of Fractional Dynamic Systems. Cambridge Academic Publishers, Cambridge.
- Leela, S., Lakshmikantham, V. and Devi, J.V. (2012) Theory of Fractional Dynamic Systems. Cambridge Scientific Publishers, Cambridge.
- Gutiérrez, R.E., Rosário, J.M. and Machado, J.T. (2010) Fractional Order Calculus: Basic Concepts and Engineering Applications. Mathematical Problems in Engineering, 2010, Article ID: 375858, 19 Pages.
- Trzaska, M. and Trzaska, Z. (2011) Chaotic Oscillations in Fractional-Order Nonlinear Circuit Models of Bipolar Pulsed Electroplating, 20th European Conference on Circuit Theory and Design (ECCTD), Linkoping, 29-31 August 2011, 165-168.
- Yulmetyev, R.M., Yulmetyeva, D. and Gafarov, F.M. (2005) How Chaosity and Randomness Control Human Health. Physica A, 354, 404-414. http://dx.doi.org/10.1016/j.physa.2005.02.036
- Machado, J.A.T. (2002) Nonlinear Dynamics. An International Journal of Nonlinear Dynamics and Chaos in Engineering Systems. Special Issue of Fractional Order Calculus and Its Applications, 29.
- Magin, R.L. and Ovadia, M. (2008) Modeling the Cardiac Tissue Electrode Interface Using Fractional Calculus. Journal of Vibration and Control, 14, 1431-1442. http://dx.doi.org/10.1177/1077546307087439
- Sommacal, L., Melchior, P., Oustaloup, A., Cabelguen, J.-M. and Ijspeert, A.J. (2008) Fractional Multi-Models of the Frog Gastrocnemius Muscle. Journal of Vibration and Control, 14, 1415-1430. http://dx.doi.org/10.1177/1077546307087440
- Herman, R. (2011) Fractional Calculus: An Introduction for Physicists. World Scientific & Imperial College Press, River Edge.
- Podlubny, I. (1999) Fractional Differential Equations. Academic Press, San Diego.
- Trzaska, Z. (2011) Matlab Solutions of Chaotic Fractional Order Circuits. In: Assi, A., Ed., Engineering Educations and Research Using MATLAB, Intech, Rijeka.
- Lakshmikantham, V., Leela, S. and Devi, J.V. (2009) Theory of Fractional Dynamic Systems. Cambridge Scientific Publishers, Cambridge.
- Belmekki, M., Nieto, J.J. and Rodriguez-López, R. (2009) Existence of Periodic Solution for a Nonlinear Fractional Differential Equation. Boundary Value Problems, 2009, 1-18. http://dx.doi.org/10.1155/2009/324561
- Petras, I. (2011) Fractional-Order Nonlinear Systems, Modeling, Analysis and Simulation. Springer-Verlag, Berlin, Heidelberg. http://dx.doi.org/10.1007/978-3-642-18101-6
- Trzaska, M. and Trzaska, Z. (2007) Straightforward Energetic Approach to Studies of the Corrosion Performance of Nanocopper Thin-Layers Coatings. Journal of Applied Electrochemistry, 37, 1009-1014.http://dx.doi.org/10.1007/s10800-007-9341-1
- Mainardi, F. (1996) Fractional Relaxation-Oscillation and Fractional Diffusion-Wave Phenomena. Chaos, Solitons & Fractals, 7, 1461-1477. http://dx.doi.org/10.1016/0960-0779(95)00125-5
- Cafagna, D. and Grassi, G. (2008) Fractional-Order Chua’s Circuit: Time-Domain Analysis, Bifurcation, Chaotic Behavior and Test for Chaos. International Journal of Bifurcation and Chaos, 18, 615-639.http://dx.doi.org/10.1142/S0218127408020550
- Jerri, A.J. (1998) The Gibbs Phenomenon in Fourier Analysis, Splines and Wavelet. Kluwer, Dordrecht. http://dx.doi.org/10.1007/978-1-4757-2847-7
- Trzaska, Z. (2008) Fractional-Order Systems: Their Properties and Applications. Elektronika, 49, 137-144.
- Trzaska, Z. (2012) Fractional-Order Harmonic Oscillators. Elektronika, 53, 162-167.
- Trzaska, Z. (2010) Chaos in Fractional Order Circuits. Electrical Review, 86, 109-111.
- Trzaska, Z. (2009) Fractional Order Model of Wien Bridge Oscillators Containing CPEs. Proceedings MATHMOD’09 Conference, Vienna, 357-361.
- Luo, Y. and Chen, Y.Q. (2012) Fractional Order Motion Controls. John-Wiley and Sons Inc., New York. http://dx.doi.org/10.1002/9781118387726
- Chen, Y.Q., Vinaigre, B.M., Xue, D. and Feliu, V.E. (2010) Fractional-Order Systems and Controls: Fundamentals and Applications. Springer, Berlin, New York.
- Li, M., Lim, S.C. and Chen, S. (2011) Exact Solution of Impulse Response to a Class of Fractional Oscillators and Its Stability. Mathematical Problems in Engineering, 2011, Article ID 657839.

