Advances in Pure Mathematics
Vol.3 No.5(2013), Article ID:35429,4 pages DOI:10.4236/apm.2013.35069
Best Simultaneous Approximation of Finite Set in Inner Product Space
Department of Mathematical Sciences, Shahrood University of Technology, Shahrood, Iran
Email: Akbarzade.s.h@gmail.com, m.iranmanesh2012@gmail.com
Copyright © 2013 Sied Hossein Akbarzadeh, Mahdi Iranmanesh. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 12, 2013; revised June 13, 2013; accepted July 15, 2013
Keywords: Best Approximation; Hyperplane; Best Simultaneous Approximation
ABSTRACT
In this paper, we find a way to give best simultaneous approximation of n arbitrary points in convex sets. First, we introduce a special hyperplane which is based on those n points. Then by using this hyperplane, we define best approximation of each point and achieve our purpose.
1. Introduction
As we known, best approximation theory has many applications. One of the best results is best simultaneous approximation of a bounded set but this target cannot be achieved easily. Frank Deutsch in [1] defined hyperplanes and gave the best approximation of a point in convex sets.
In [3,4] we can see that a hyperplane of an n-dimensional space is a flat subset with dimension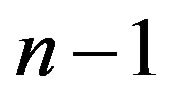 .
.
In this paper we try to find best simultaneous approximation of n arbitrary points in convex sets. We say theorems of best approximation of a point in convex sets.
Then we give the method of finding best simultaneous approximation of n points in convex set.
2. Preliminary Notes
In this paper, we consider that X is a real inner product space. For a nonempty subset W of X and 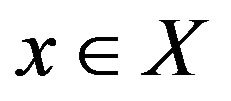 , define
, define
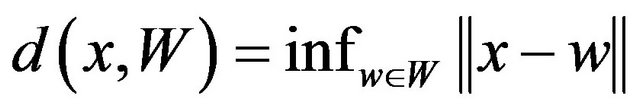 .
.
Recall that a point 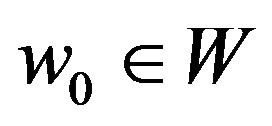 is a best approximation of
is a best approximation of 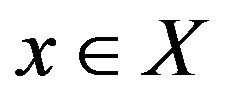 if
if 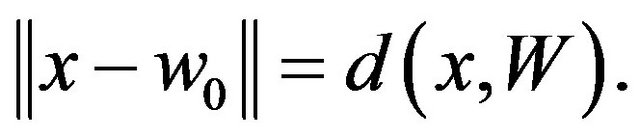
If each  has at least one best approximation
has at least one best approximation 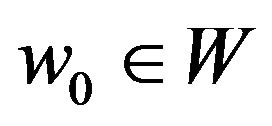 , then W is called proximinal.
, then W is called proximinal.
We denote by 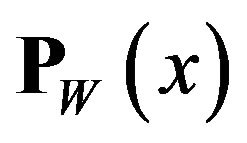 , the set of all best approximations of x in W. Therefore
, the set of all best approximations of x in W. Therefore
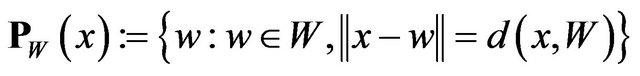
It is well-known that 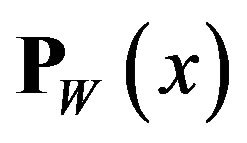 is a closed and bounded subset of X. If
is a closed and bounded subset of X. If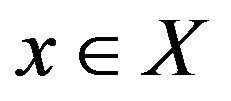 , then
, then 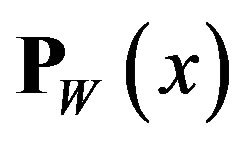 is located in the boundary of W.
is located in the boundary of W.
In 2.4 lemma of [1] we can see that if K be a convex subset of X. Then each 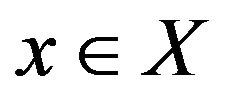 has at most one best approximation in K.
has at most one best approximation in K.
In particular, every closed convex subset K of a Hilbert space X has a unique best approximation in K.
Also in 4.1 lemma of [1] if K be a convex set and ,
, 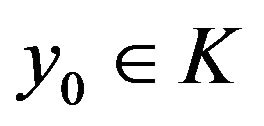 . Then
. Then 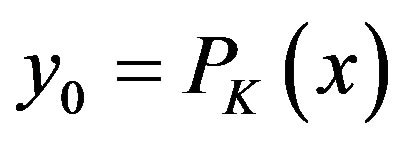 if and only if
if and only if
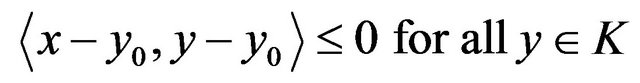
For a nonempty subset W of X and a nonempty bounded set S in X, define
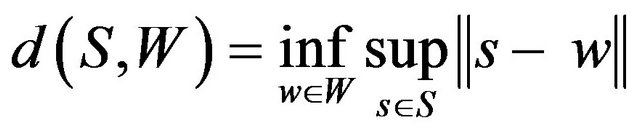
and
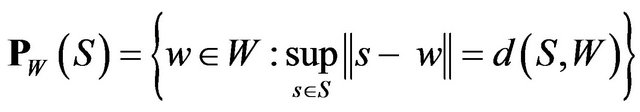
Each element in  (If
(If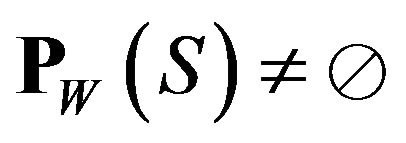 ) is called a best simultaneous approximation to S from W (see [2] Preliminary Notes).
) is called a best simultaneous approximation to S from W (see [2] Preliminary Notes).
For 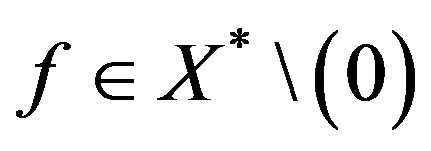 and
and 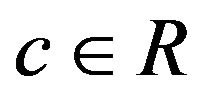 hyperplane H in X defined by
hyperplane H in X defined by
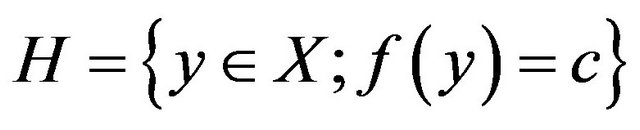
and we denote H by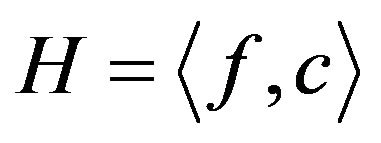 .
.
The Kernel of a functional f is the set
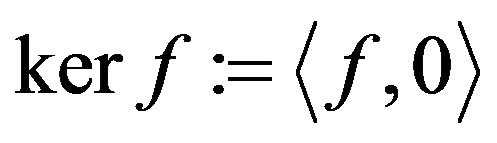
and for
 we say that
we say that 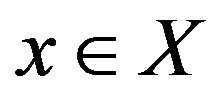 is in the below of hyperplane H, if
is in the below of hyperplane H, if  .
.
3. Best simultaneous Approximation in Convex Sets
In this section,we consider
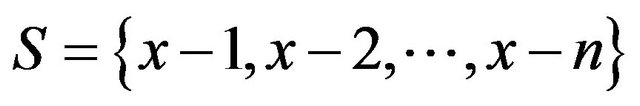
and
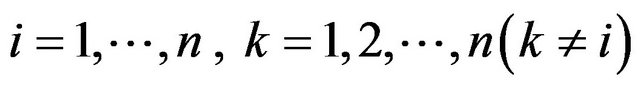
Define
 (1.1)
(1.1)
Lemma 3.1. Let 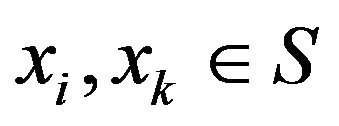 consider the hyperplane
consider the hyperplane 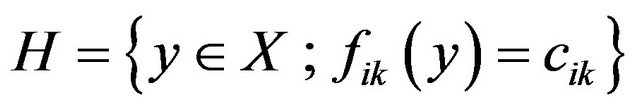 then
then
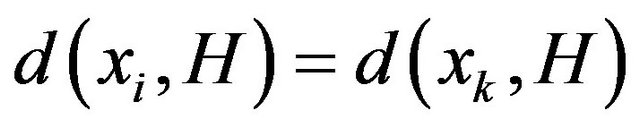
Proof. Give  so we have
so we have
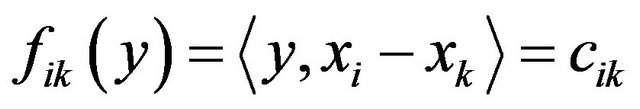
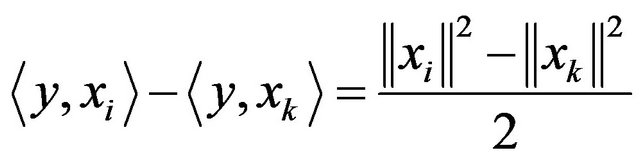
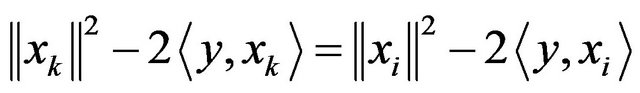
So by adding 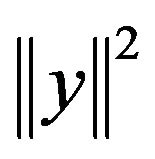 with equation of above, we have
with equation of above, we have
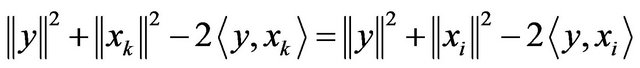
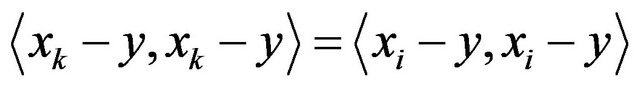
Therefore have

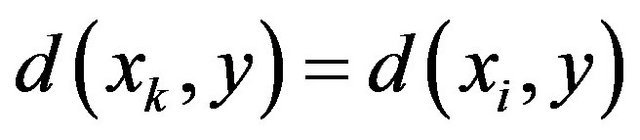 ■
■
Note 3.2. It is obvious that 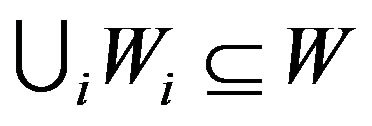 . Now let
. Now let  , so there exist
, so there exist  such that
such that 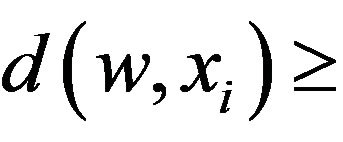
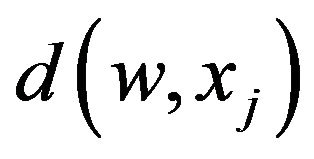 for all
for all 
Thus ![]() , therefore w will be in Wi, that we conclude
, therefore w will be in Wi, that we conclude
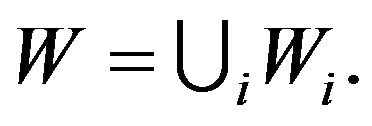
Theorem 3.3. Let 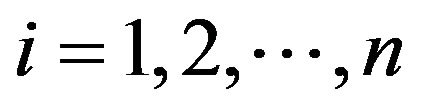 then:
then:
1) 
2) If W be a convex subset of X, then Wi is a convex set.
3) If W be a closed set, then Wi is a closed set.
Proof. 1) Let 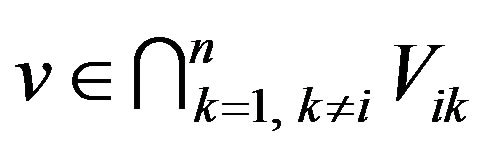 therefore
therefore
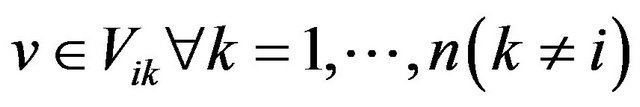 so
so 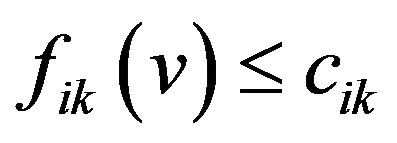 then we have
then we have
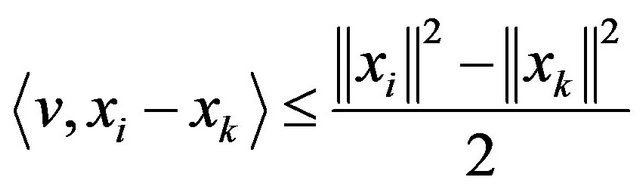


so by adding  with equation of above, we have
with equation of above, we have
![]()
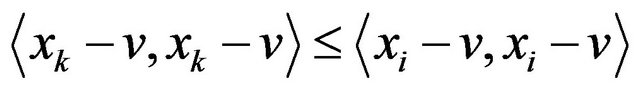
therefore we have
![]()
 .
.
Thus we have
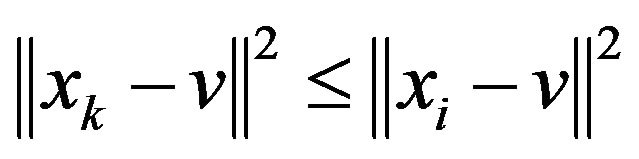
 .
.
Therefore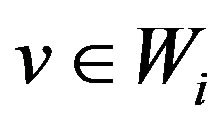 .
.
Since all previous steps will be reversible, so for any 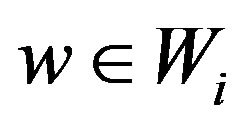 in a fixed i, we have
in a fixed i, we have 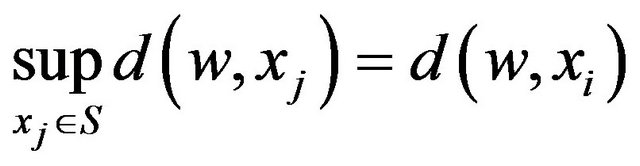 that consider
that consider
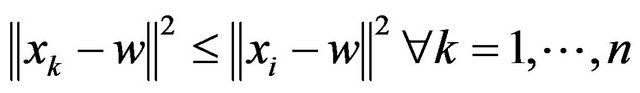
thus we have
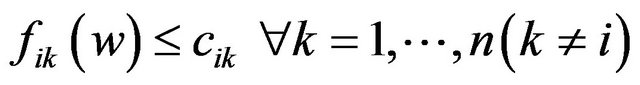
so
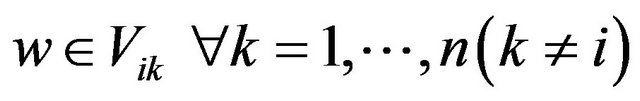
therefore
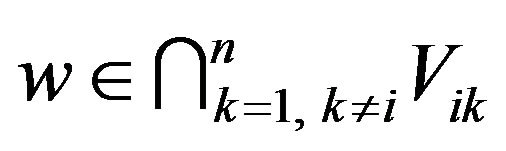
and finally
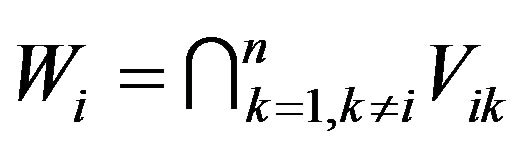 .
.
2) First we proof 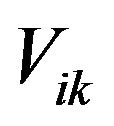 , for all
, for all 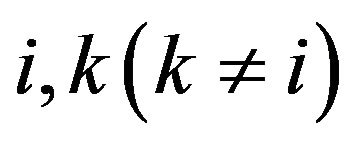 is convex set.
is convex set.
Give 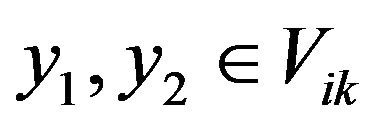 and
and 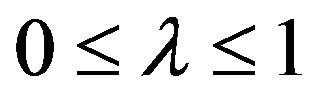 , set
, set

thus we have
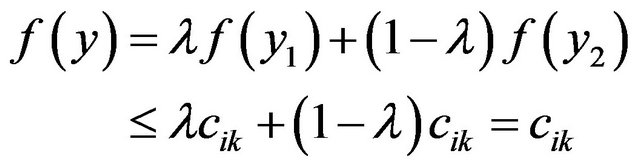
So 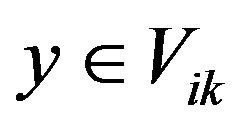 . Thus
. Thus 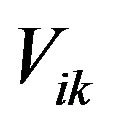 is convex set and since intersection of any convex set is convex, therefore Wi is convex set.
is convex set and since intersection of any convex set is convex, therefore Wi is convex set.
3) It is obviously that f is continuous function and we know
 .
.
So, 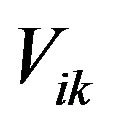 is closed set, this implies Wi is closed set. ■
is closed set, this implies Wi is closed set. ■
4. Algorithm
The following theorem states that to find best simultaneous approximation of a bounded set S of W, it is enough to obtain the best approximation to any
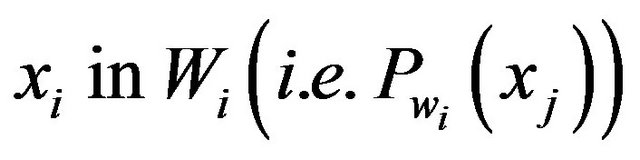 .
.
Thus 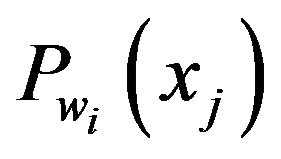 would be the best simultaneous approximation of S from W if
would be the best simultaneous approximation of S from W if 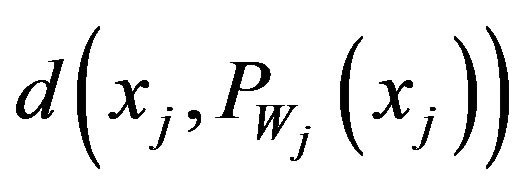 is minimal.
is minimal.
Theorem 4.1. If W be a convex subset of X and there exist  for all
for all 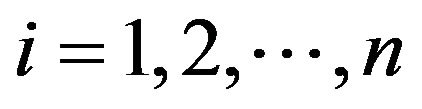 , then
, then
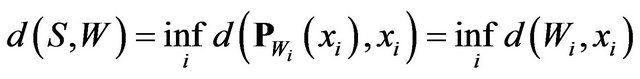
Proof. With attention of best simultaneous approximation and (3.2) notation, we have
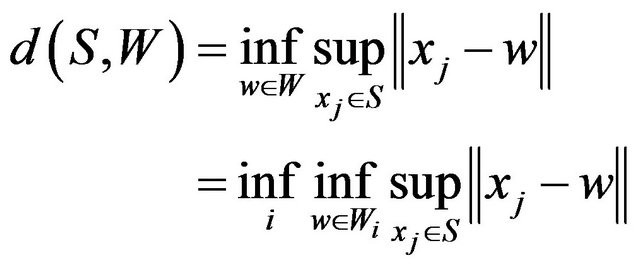
but according to the definition of Wi we have
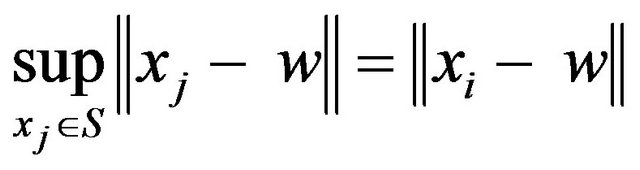
thus the above equation can be written as follows
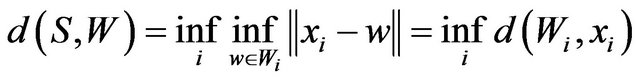
and since exist
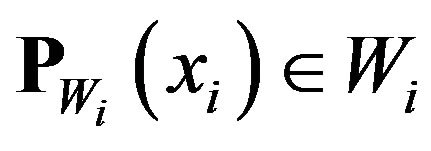
so we have
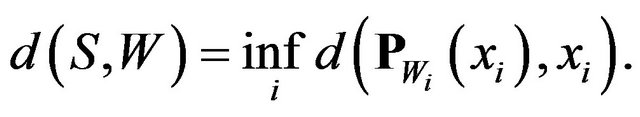 ■
■
Corollary 4.2. With the assumptions of the previous theorem there exist i, such that 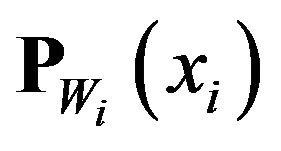 is best simultaneous approximation of S in W.
is best simultaneous approximation of S in W.
Proof. With attention previous theorem, there exist 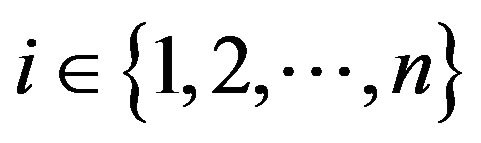 such that
such that
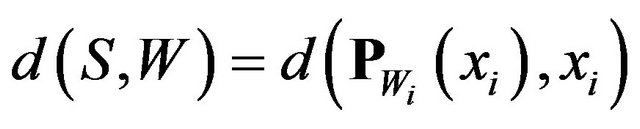
and by the definition of 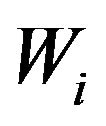 we have
we have
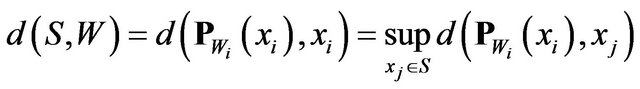
after according to the above equation and define the best simultaneous approximation of the relationship will
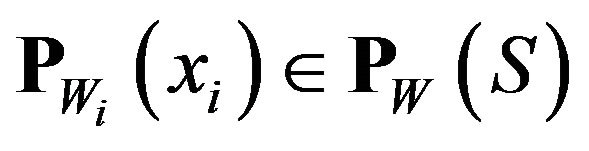
However, the algorithm with assumes a convex set W and  introduce the following.
introduce the following.
With attention 3.1 lemma for points x1, x2 the hyperplane 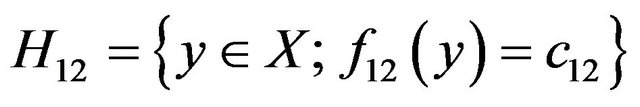 are possible to obtain, by 3.4 definition the points W in below H12 are V12 called.
are possible to obtain, by 3.4 definition the points W in below H12 are V12 called.
Also for points x1, x3 the hyperplane
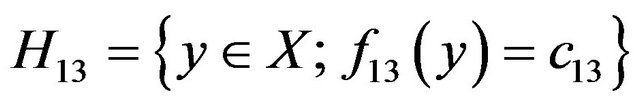
are formed and the points of W in below H13 are V13 called and so we do order to the points x1, xn.
By taking subscribe of any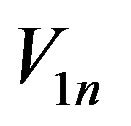 , find W1 that this set is convex (by Theorem 3.3, 2).
, find W1 that this set is convex (by Theorem 3.3, 2).
Therefore, if best approximation x1 exists in this set, it is called 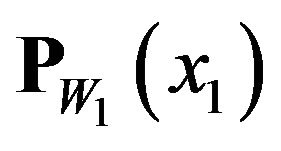 . Thus obtain
. Thus obtain 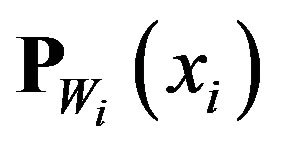 for any
for any
 .
.
Finally, the point ![]() which has minimal distance to xi, is the best simultaneous approximation of S in W.
which has minimal distance to xi, is the best simultaneous approximation of S in W.
REFERENCES
- F. Deutsch, “Best Approximation in Inner Product Spaces,” Springer, Berlin, 2001.
- D. Fang, X. Luo and Chong Li, “Nonlinear Simultaneous Approximation in Complete Lattice Banach Spaces,” Taiwanese Journal of Mathematics, 2008.
- W. C. Charles, “Linear Algebra,” 1968, p. 62.
- V. Prasolov and V. M. Tikhomirov, “Geometry,” American Mathematical Society, 2001, p. 22.

